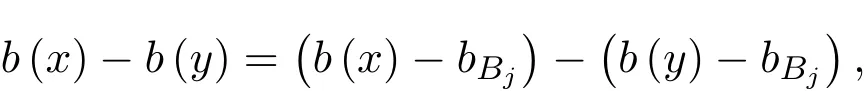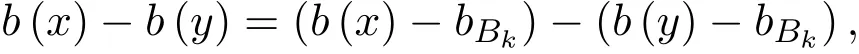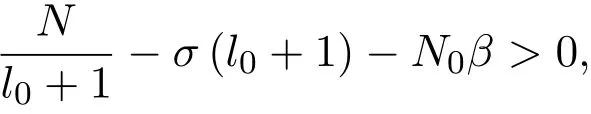一类 Schr¨odinger型算子在 Herz-Morrey空间上的有界性
2018-10-10方小珍孙爱文束立生
方小珍,孙爱文,束立生
(安徽师范大学数学与统计学院,安徽 芜湖 241003)
1 引言
设 L=−∆+V(x)是 Rn(n≥3)上(的 Sc)hr¨odinger微分算子,其中 V(x)是非负但不为零的位势,且属于反向 H¨older类 Bs.自 1995年文献 [1]给出了具有非负位势的 Schr¨odinger算子在经典Lebesgue空间上的有界性以来,与Schr¨odinger算子相关的研究取得了突破性进展.文献 [2-3]得到了算子 Vβ2(−∆+V)−β1及其对偶算子的有界性估计.在文献[4]中,作者研究了与L相关的Riesz变换及分数积分算子的端点估计.更多与L相关的研究成果见文献[5-6].
奇异积分交换子是调和分析研究中的重要内容.令Tβ=(−∆+V)−βVβ是与L相关的算子且b∈BMOσ(ρ).在文献[1]的研究基础上,2016年文献[7]利用极大估计先后得到了交换子[b,Tβ]在Lp空间和Herz空间上的有界性.文献[8]研究了与L相关的奇异积分交换子的加权估计.基于以上研究,本文主要讨论 Tβ及其交换子 [b,Tβ]在 Herz-Morrey空间上的有界性.
在这篇文章中,将球B⊂Rn的Lebesgue{测度记为|B|,C}和C′表示为未指定的正常数,在每个地方取值可能不同.∀k∈Z,令Bk=x∈Rn:|x|≤2k,且 Ek=BkBk−1,记函数Ek的特征函数为χk.U∼V表示存在常数C>0及C′>0,使得C′V≤U≤CV.
首先,介绍相关定义.
定义 1.1[1]设V(x)是Rn上的非负局部Ls可积函数,若存在常数C>0,使得下面的反向 H¨older不等式

对 Rs上所有球B 都成立,则称V(x)属于反向H¨older类Bs(s>1).
定义 1.2[1]设x∈Rn,V∈Bs(s>1),辅助函数ρ(x)定义如下:

定义1.3[7]设b∈,σ∈(0,∞),ρ(x)为定义 1.2中所定义的辅助函数,一个新的 BMOσ(ρ)空间定义为:

其中球
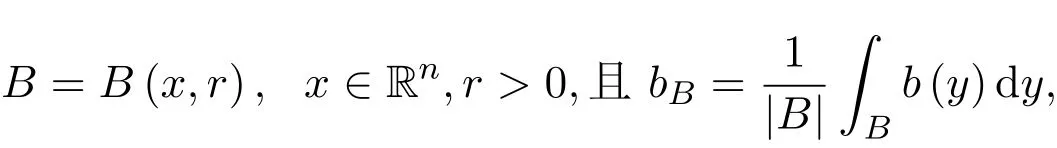
一般也将 ∥b∥BMOσ(ρ)简记为 ∥b∥σ.
定义1.4[8]设则与 Schr¨odinger算子 L相关的算子定义为:Tβ=(−∆+V)−βVβ.且记 kβ(·,·)为算子 Tβ的核.
定义 1.5[9]若 α∈R,0 其中 引理2.1[1]设V∈Bs,s≥.则 V(y)dy为双倍测度.即存在常数 C0>0,使得 ∀r>0,x∈Rn有 引理 2.2[1]存在常数C>0,l0>0,使得∀x,y∈Rn,有下面的: 引理2.3[7]设.∀N ∈N,存在常数 CN>0,使得 (a)若j≤k−2,则 (b)若j≥k+2,则 引理2.5[10]设 其中常数C仅依赖于N,s,β,与其他主要参数无关. 其中常数C依赖于N,s,β,与其他主要参数无关. 引理 2.6[11]令σ>0,1 有 这里l0同引理2.2所定义. 引理 2.7[11]令σ>0,k∈N,且 1 则有 这里l0同引理2.2所定义. 引理2.8[12]设(C0为引理2.1中所定义),存在一个常数 CN0>0,使得 ∀x∈Rn及 r>0,有 其中常数C仅依赖于ρ(0),N,l0,β,与其他主要参数无关. 定理2.1的证明 记 于是 对于I2,由引理2.5,Tβ在Lq上有界可得 估计I1.对 x∈Ek,y∈Ej,且j≤k−2,有 |x−y|∼|x|.由(1.1)式,引理2.4,引理2.8及 H¨older不等式,有 最后估计I3.对x∈Ek,y∈Ej,j≥k+2,有|x−y|∼|y|,则 对于J2,由引理2.5,[b,Tβ]在Lq上的有界,可得 下面估计J1.由于 则 由于 x∈Ek,y∈Ej,且 j≤k−2,有 |x−y|∼|x|.根据 (1.1)式,引理 2.4,引理 2.7,引理 2.8及 H¨older不等式,有 对于J12,由引理2.4,引理2.6,引理2.8得 取N 足够大,使得 则 最后估计J3.由于 则 由于x∈Ek,y∈Ej,且j≥k+2,则 |x−y|∼|y|,故 因此取N 足够大,使得 则有 综上,定理2.2证毕.

2 引理及主要结果



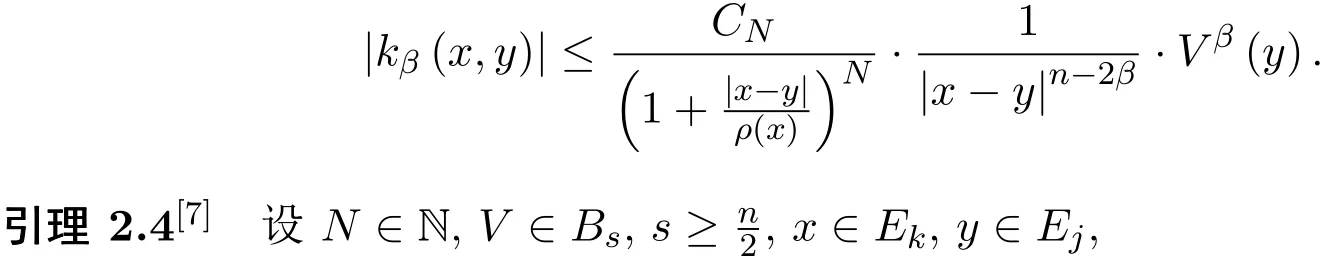


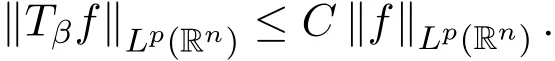







3 主要结果的证明