Variation of power type functional about mean curvature of submanifolds

Liu Jin

(College of Systems Engineering,National University of Defense Technology,Changsha 410073,China)

Abstract：For an n-dimensional submanifold in a general real ambient manifold φ:Mn→Nn+p,let H2denote the square length of mean curvature vector of φ.In this paper,we introduce one power type functional concerning H2as M(n,r)(φ)= ∫M(H2)rdv,where r is a real number,which measures how derivations φ(M)from a minimal submanifold and has a close relation with the well-known Willmore Conjecture.For this functional,the first variational equation is obtained.Moreover,in unit sphere,we construct a few examples of critical points.

Keywords：mean curvature,minimal submanifolds,Willmore conjecture,critical point

1 Introduction

Let φ :Mn→ Nn+pbe an n-dimensional compact without boundary submanifold in a general ambient manifold.Sometimes we choose Nn+pto be(n+p)-dimensional space forms Rn+p(c).It is well-known that when c=1,0,−1,Rn+p(c)is the standard unit sphere Sn+p(1),Euclidean space En+pand hyperbolic space Hn+p(−1)respectively.Choose an orthonormal frame fields{e1,···,en,en+1,···,en+p}along M such that{e1,···,en}are tangent to M and{en+1,···,en+p}are normal to M.Their dual frame fields are{θ1,···,θn}and{θn+1,···,θn+p}respectively.It is well known that θn+1= ···= θn+p=0 when they are restricted over M.Throughout this paper,we employ the Einstein summation convention,which states that repeated copies of the same index are summed over.Additionally,we adopt the following convention for the range of the various indices:

Let II denote the second fundamental form of the submanifold φ :Mn→ Nn+p,which can be expressed in terms of the frame fields and their duals as:

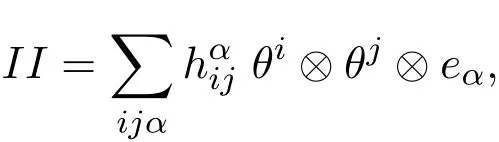
where⊗ denotes the tensor product anddenotes the tensor components of the second fundamental form.Additionally de fi ne the following quantities:

where⃗H is the mean curvature vector,S is the square of the length,and ρ is the Willmore invariant of II.It is well-known that the submanifold φ:Mn→Nn+pis minimal when⃗H≡0 and is totally geodesic when S ≡ 0.The Willmore invariant ρ,has the following properties:(i)for all x ∈ M,ρ(x)≥ 0;(ii)ρ(x)=0 if and only if x is an umbilical point of M;and(iii)since M is compact,0≤ρ(x)≤C for all x∈M and some positive constant C.

In differential geometry,there is a famous classic Willmore functional for submanifold in unit sphere φ :Mn→ Sn+p(1)which is def i ned as

see references[1-4]for the details.It is well known that this functional is invariant under conformal transformation.Its critical point is called classic Willmore or W(n,n2)-Willmore submanifold.The famous Willmore conjecture says that W(2,1)(φ)≥ 4π2holds for all immersed tori φ :M →S3,recently it has been completely solved by F.C.Marques and A.Neves in reference[5]using Min-Max theory for two dimensional surfaces,but higher dimensional case is still an open problem.When n≥3,the functional W(n,n2)(φ)was studied extensively in references[6-11].

Due to the importance of Willmore conjecture,many geometric experts generalized the classic Willmore functional to a wide range and some interesting results have been obtained.In reference[12],Cai studied the W(2,p)-Willmore functional for surfaces in 3-dimensional unit sphere S3(1)as W(2,p)(φ)= ,where p is a real number,k1,k2denote the principal curvatures of M and k1≥k2.Under some proper conditions,Cai obtained some global interesting inequalities.In reference[13],Guo and Li considered the W(n,1)-Willmore functional for submanifolds in unit sphere φ :Mn→ Sn+p(1)as W(n,1)(φ)= ∫Mρdv.They calculated the first variation and constructed a few examples of critical points of W(n,1)(φ).In reference[14],Wu researched the W(n,r)-Willmore functional for submanifolds in unit sphere φ :Mn→ Sn+p(1)as W(n,r)(φ)= ∫Mρrdv,where r is a real number.Using the basic calculation technique developed in reference[10],Wu calculated the first variation formula and constructed some examples of W(n,r)(φ).

Motivated by the work mentioned above,we focus the functionals about mean curvature,it would be interesting to study the following three functionals

where r is a real number.Obviously,M(n,n2)(φ)and M(n,1)(φ)are special cases of M(n,r)(φ).

Functionals M(n,n2)(φ)and M(n,1)(φ)have a close relation with Willmore conjecture.In fact,when n=2 and φ:M2→ S3(1),the original Willmore conjecture proposed in references[2-4]expressed by M(n,1)(φ).When n ≥ 3,in reference[15],Chen estimated the lower bound of M(n,n2)(φ).Recently,in reference[16],Guo and Yin calculated the fi rst variational equation of M(n,n2)(φ)and explored the relationship between M(n,n2)(φ)and the classic Willmore functional W(n,n2)(φ).

Above all,it is natural to study the functional M(n,r)(φ).In geometric meaning,the functional measures how derivations φ(M)form a minimal submanifold and generalize the well-known classic Willmore functional.In this paper,we study the variational problem of M(n,r)(φ).

The rest of this paper is organized as follows.In section 2,the structure equations of submaifolds and the variation formulas of the second fundamental form are established.In section 3,using the basic formulas in section 2,we calculate the fi rst variation of M(n,r)(φ).When the ambient manifold Nn+pis unit sphere,in section 4,according to the formulas in section 3,we construct some examples of critical points of M(n,r)(φ).

2 Structure equations and basic variation formulas

Let φ :Mn→ Nn+pbe an n-dimensional compact submanifold without boundary in an(n+p)-dimensional general ambient manifold,and Φ(·,·):Mn×(−ϵ,ϵ) → Nn+pbe a variation of φ.This means that φt=:Φ(·,t):Mn×{t} → Nn+p, ∀t∈ (−ϵ,ϵ)is an isometric immersion with φ0≡ φ.

Let s=(s1,···,sn,sn+1,···,sn+p)and σ =(σ1,···,σn,σn+1,···,σn+p)be the orthonormal local frame fi elds of tangent vector bundle TNn+pand cotangent vector bundle T∗Nn+p,respectively.Then,e=(e1,···,en,en+1,···,en+p)= φ−t1s is the set of orthonormal local frame fi elds of the pull-back vector bundle φTNn+pover Mn×{t}.Note since:

{e1,···,en}are tangent to Mnand{en+1,···,en+p}are normal to Mn.

Let ω denote the connection form over TNn+p.By the pull-back operation,we can assume the following decomposition:

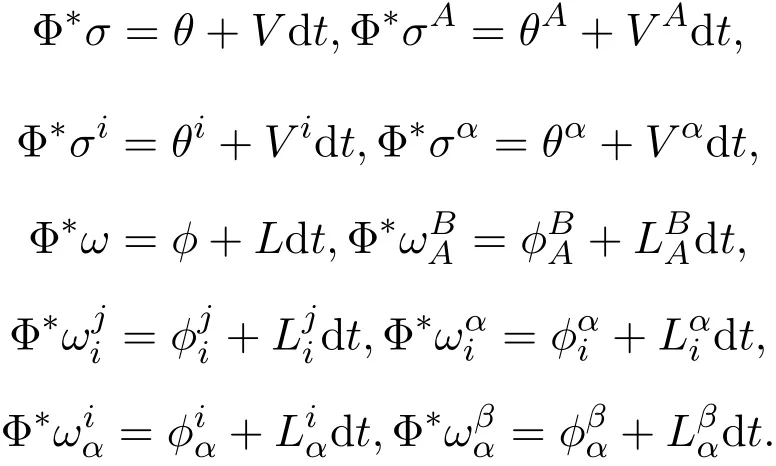
From submanifold theory or reference[17],it is well known that{θi}are the orthonormal frame fi elds ofis the connection form of TMn,{}is the connection form of T⊥Mn,is the second fundamental form,and θn+1≡ ···≡ θn+p≡ 0 when they are restricted over Mn.

One can also derive that{Vi,Vα}are the variation vector fi elds of Φ,meaning that:

It must be mentioned that in variational theory,generally speaking,the tangential variation vector fi elds∑

iVieihave little role in the calculations.So,we assume in this paper that only normal variation vector fi elds need to be considered:

From the second fundamental form,we can construct some notations which are useful in the variation calculation.First,when the codimension of submanifold φ :Mn→ Nn+pis 1,it means Mnis a hypersurface,we can introduce

Second,when the codimension of φ :Mn→ Nn+pis greater than 1,we can introduce

Let Ω,Ω⊤,and Ω⊥denote the curvature forms of TNn+p,TMn,and T⊥Mn,respectively.Hence their components and some other algebraic identities are as follows:

where∧denotes the exterior product,¯RABCD,Rijkl,R⊥αβijdenote the Riemmanian curvature tensor components of TNn+p,TMn,and T⊥Mn,respectively.Additionally,assume that:

where Ψ denotes the pull back curvature form without dt,while P denotes 1-form with dt.

Following from the def i nitions:

Hence:

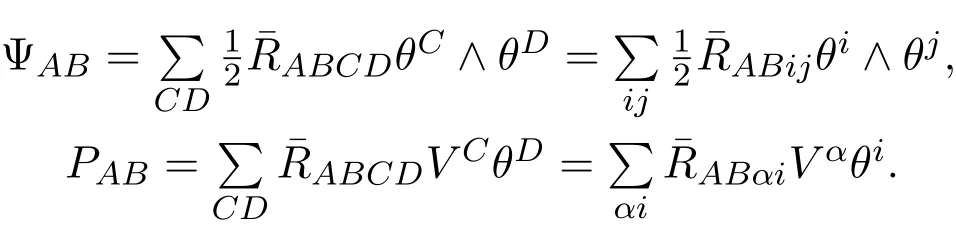
From any standard differential geometry text book or reference[17],one has the structure equations of Riemannian manifold are ω+ωT=0,dσ−σ∧ω =0,Ω+ΩT=0,Ω =dω−ω∧ω.where ωT,ΩTdenote the transpose of ω,Ω respectively.By pulling back the both sides of structure equations,one has

From(1),one has ϕ +dtL+ ϕT+dtLT=0,comparison both sides,we obtain

From(2),one has

comparison both sides,we have dMθ− θ∧ ϕ=0,=dMV+V ϕ − θL.It means

Based on(7),when index A=i or A= α,together with Vi≡ 0,θα≡ 0,we have the below lemma.

Lemma 2.1 Let φ:Mn→Nn+pbe a submanifold,andvector fi eld,one has

From(3),one has Ψ+dt∧P+ΨT+dt∧PT=0,comparison both sides,we have

From(4),one has

comparison both sides,one has

It means

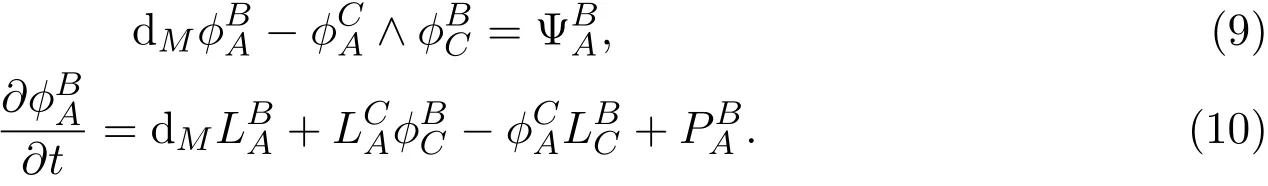
In(9),when index A=i and B=j,we have

thus we obtain the Gauss equation of submanifold

In(9),when index A= α and B= β,we have

thus we obtain the Ricci equation of submanifold

In(9),when index A=i and B=α,we have

thus we obtain the Codazzi equation of submanifold

Equations(11),(12),and(13)together lead to the below lemma.

Lemma 2.2 Let φ:Mn→ Nn+pbe a submanifold,one has structure equations

Now turn to equation(10),when index A=i and B=α,using lemma 2.1,one has

From(14),together with lemma 2.1,we have Equations(14),and(15)together lead to the below lemma.

Lemma 2.3 Let φ:Mn→Nn+pbe a submanifold,andvector field,one has

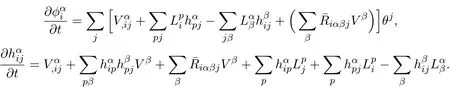
Finally,one additional lemma is useful for our purposes.

Lemma 2.4 With the same notations as above,one has

3 The first variation calculation

To calculate the fi rst variation of functional M(n,r)(φ),two additional lemmas are needed.

Lemma 3.1 Let φ:Mn→Nn+pbe a submanifold,andvector fi eld.Suppose dv= θ1∧ ···∧ θndenotes the volume element,one has

Proof By lemma 2.1,we have

Hence,

This,we complete the proof.

Lemma 3.2 Let φ:Mn→Nn+pbe a submanifold,andvector fi eld,one has

where

Proof By lemmas 2.3 and 2.4,one has

This,we complete the proof.

Use lemmas 3.1 and 3.2 together,we can calculate the first variation formula of functional M(n,r)(φ).

Theorem 3.1 Let φ :Mn→ Nn+pbe an n-dimensional submanifold in an(n+p)-dimensional general real ambient manifold Nn+p,then M is a critical point of M(n,r)(φ)if and only if for any α∈[n+1,n+p],we have

Proof Using lemmas 3.1 and 3.2,we calculate

This,we complete the proof.

From any one standard differential geometry text book or reference[17],we know the curvature of space forms Rn+p(c)are

Thus

Together with theorem 3.1,we can derive out the following corollaries.

Corollary 3.1 Let φ :Mn→ Rn+p(c)be an n-dimensional submanifold in an(n+p)-dimensional space forms Rn+p(c),then M is a critical point of M(n,r)(φ)if and only if for any α∈[n+1,n+p],

Proof In space forms,we know

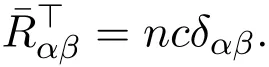
By substituting this expression into the equation(16)in theorem 3.1,one obtains the desired result.

Corollary 3.2 Let φ :Mn→ Rn+1(c)be an isoparametric(all principal curvatures are constant)hypersurface in an(n+1)-dimensional space forms Rn+1(c),then M is a critical point of M(n,r)(φ)if and only if

Proof By using the identities:

and substituting them into the equation(17)in corollary 3.1,the desired result is obtained.

4 Construction of examples

In this section,we use equations in theorem 3.1 and its corollaries to explore critical points of M(n,r)(φ)in unite sphere,the main technique used is to solve algebraic equations.

Example 4.1 Totally geodesic submanifolds in unit sphere are critical points of M(n,r)(φ).

Example 4.2 According to the equation(17),we know all minimal submanifolds in unit sphere φ :Mn→ Sn+p(1)are critical points of M(n,r)(φ).

Example 4.3 Let φ :Mn→ Sn+1(1)is a totally umbilical but not totally geodesic hypersurface in unit sphere,according to the def i nition,suppose all principal curvatures are

Through a direct calculation,we obtain

substituting them into the equation(18),we have an algebraic equation of critical points of M(n,r)(φ),

If λ is f i xed,then the parameter r must be

If r is f i xed,then λ must be

and r should satisfy

Example 4.4 For a particular hypersurface with n≡0(mod 2)

All principal curvatures are

We can derive the quantities H=0,S=n respectively,substituting them into equation(18),we knowalways is a critical point of M(n,r)(φ).

Example 4.5 For a family hypersurfaces with parameter λ, µ,0< λ,µ <1,λ2+µ2=1,

Obviously,all principal curvatures are

Then the quantities H,S are respectively

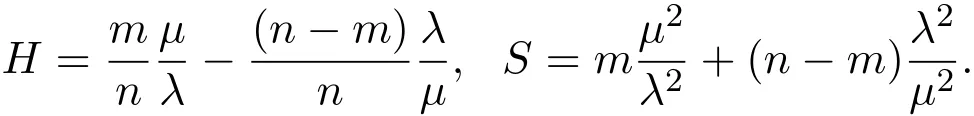
or

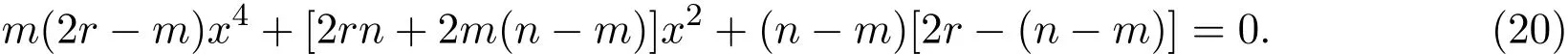
From reference[17],we know the solution of(19)are clif f ord torus

which are minimal.While the equation of(20)essentially are 2 order polynomial,which can be solved completely,but depends on the parameter pair(n,r),and the solutions of(20)are not minimal but are critical points of M(n,r)(φ).

Example 4.6 Let(x,y,z)be a natural coordinates of R3and(u1,u2,u3,u4,u5)be the natural coordinate system of R5,we consider the mapping as below

this mapping def i ned an isometricsurface.From reference[18],we know

Then we calculate

Substituting them into the equation(17),one can conclude that Veronese surface always is a critical point of M(n,r)(φ).

Example 4.7[19]Let

Let E be the space of(m+1)×(m+1)symmetric matrices(uij)m×msuch that

it is a vector space of dimensionm(m+3).We de fi ne the norm in E by

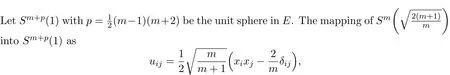
which is an isometric minimal immersion.Thus according to the Example 4.2,we can conclude it is a critical point of M(n,r)(φ).

Example 4.8[19]We can def i ned a minimal immersion of m-dimensional complex pro-with holomorphic section curvatureinto a unit sphere Sm(m+2)−1(1)such that the usual coordinate functions of Rm(m+2)are independent hermitian harmonic func-.Thus according to the Example 4.2,we can conclude that it is a critical point of M(n,r)(φ).

Example 4.9 Let

be a submanifold canonically embedded into the unit sphere Sn+p−1,where involved parameters satisfy

In fact,consider

and

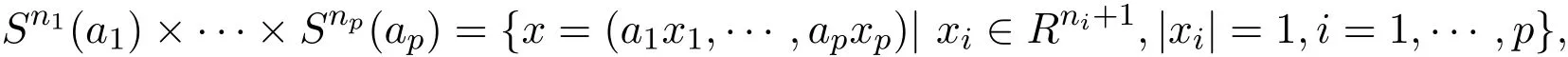
where

is the canonical embedding.Suppose the(p−1)orthogonal normal vector fields of M are

where(aλ1,···,aλp)satisfies the p × p matrix

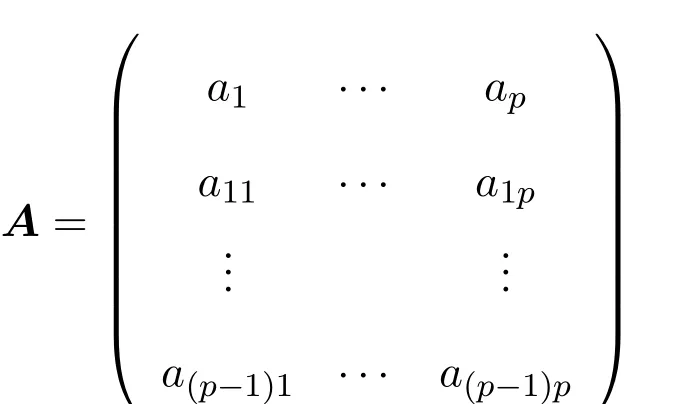
is an orthogonal normal matrix,thus

Therefore the first fundamental form and second fundamental form of M are given by

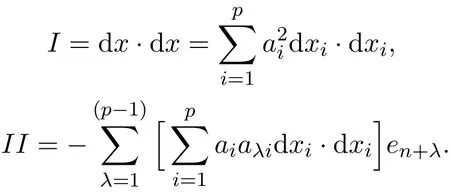
We get the components of the second fundamental form

where Eiis the ni×niunit matrix,through directly calculation,we get

Substituting the above all into equation of Theorem 3.1,we can get an algebraic equation of critical points of M(n,r)(φ).