平面控制网中误差曲线及相对误差曲线的绘制及应用
2018-10-09马慧
马 慧
(山东科技大学,山东 泰安 271000)
在测量中,控制网的精度评定是一个重要的内容。为了评定其中待定点的精度,常采用点位误差椭圆,但是,点位误差椭圆的中心与椭圆曲线上点的连线不是中误差的大小,点位误差曲线才真正反映实际的中误差大小,所以本文中给出了衡量待定点精度的误差曲线以及待定点之间的相对误差曲线。同时,这些曲线是借助于AutoCAD来进行绘制的。
1 理论部分
1.1 误差椭圆的要素
1.1.1误差椭圆的要素[1]
要绘制一个误差椭圆,需要知道误差椭圆的中心坐标、位差极大值E和位差极小值F、位差极大值方向φE,其中E,F和φE称为误差椭圆的三参数。
1.1.2误差椭圆的参数计算公式[2]
QEE=(QXX+QYY+K)/2,QFF=(QXX+QYY-K)/2,
设两个待定点为Pi和Pk,这两点的相对位置可通过坐标差来表示,即:
Δxik=xk-xi,Δyik=yk-yi
(1)
根据协因数传播律则得:
QΔxΔx=Qxkxk+Qxixi-2Qxkxi
(2)
QΔyΔy=Qykyk+Qyiyi-2Qykyi
(3)
QΔxΔy=Qxkyk-Qxkyi-Qxiyk+Qxiyi
(4)
得到两点间相对误差椭圆的三个参数公式:
(5)
(6)
(7)
1.2 误差椭圆与误差曲线的关系
基于点位误差椭圆,依据几何关系,可以绘制出点位误差曲线[3,4],如图1所示。设误差椭圆上的一点为P点,过P点做垂直于方向Ψ的切线,则垂足D点即为误差曲线上的一点,OD的长度即为该方向的中误差。
1.3 误差曲线的绘制方法
先确定某直线与椭圆相切,不关心该切线与椭圆的交点(x0,y0)是多少,过椭圆中心作与该切线垂直的方向线,由此确定垂足,该垂足即为误差曲线上的点;依此作该椭圆的若干切线,从而确定若干垂足。这一过程可由AutoCAD的“切点”“垂足”等相关命令来实现。
2 实际算例
2.1 算例[6]
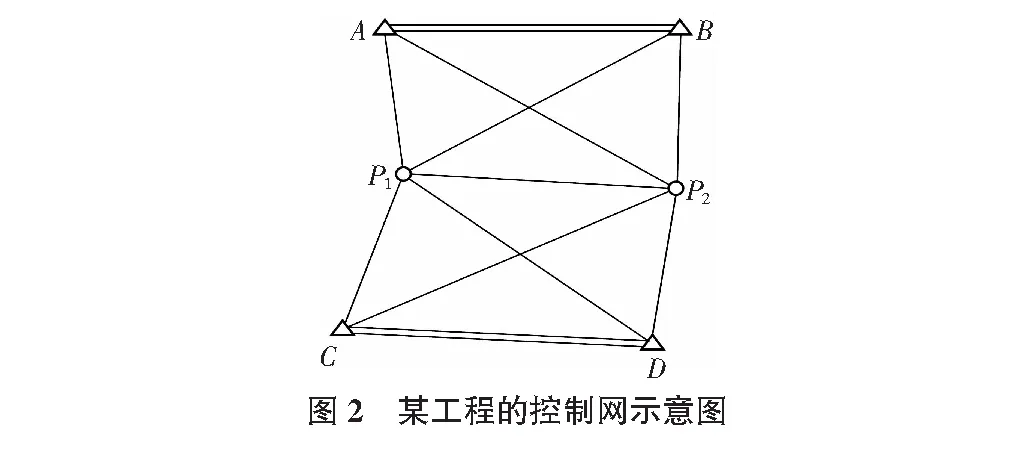
如图2所示,P1及P2是待定点,且P1,P2两点间为一山头,某条铁路专用线在此经过,要在两点间开掘隧道,要求在贯通方向和贯通重要方向上的误差不超过±0.5 m和±0.25 m。根据实地勘察,在地形图上设计了专用贯通测量控制网,已知点A,B,C及D,同精度观测了9条边长,设P1,P2点坐标为未知数[x1y1x2y2]T,经间接平差算得参数的协因数阵为:

2.2 算例解算
2.2.1各分量及其间的协因数
Qx1x1=0.344 9,Qx1y1=-0.000 9,Qx1x2=0.059 7,
Qx1y2=-0.080 7,Qy1y1=0.573 9,Qx2y1=-0.079 8,
Qy1y2=0.107 4,Qx2x2=0.345 9,Qx2y2=0.022 1,Qy2y2=0.580 4。
2.2.2计算P1,P2点的误差椭圆三要素
KR-RCA是在上述算法的基础上加入正则化和核化,本文采用E Meyers[18]提出的KR-RCA,核函数采用线性核函数,具体算法本文不再赘述。
P1点:φE1=90.225 175 282°或270.225 175 282°,E1=0.402 dm,F1=0.311 dm;
P2点:φE2=84.662 885 86°或264.662 885 86°,E2=0.401 dm,F2=0.314 dm。
2.2.3计算P1,P2两点间相对误差椭圆三要素
φE=67.684 064 59°或247.684 064 59°;E=0.534 dm;F=0.374 dm。
2.2.4判断

ψP1P2+90°=122.315 932 41°。
所以,在P1,P2连线的垂直方向的位差:

在P1,P2连线的方向的位差:

可知,在贯通方向满足要求,在贯通重要方向不满足要求,因此需要对网形进行改正。
2.2.5绘制误差曲线和相对误差曲线
先利用误差椭圆的三要素,绘制出P1,P2点的误差椭圆和它们的相对误差椭圆[7],然后,依据误差椭圆与误差曲线之间的关系,从而绘制两点的误差曲线[8],如图3所示。

3 结语
通过以上的计算及误差曲线的绘制过程,可以看出,误差曲线的绘制也是相对简单的,而且容易实现,因此,在进行精度评定时,可以根据实际情况给出待定点的误差曲线。
