Finite-time Stabilization of the Double Integrator Subject to Input Saturation and Input Delay

Huawen Ye,Meng Li,Chunhua Yang,and Weihua Gui

Abstract—The time-optimal control design of the double integrator is extended to the fnite-time stabilization design that compensates both input saturation and input delay.With the aid of the Artstein’s transformation,the problem is reduced to assigning a saturated fnite-time stabilizer.

I.INTRODUCTION

AS an extension of time-optimal control,Bhat Bernstein proposed a saturated fnite-time stabilizer for the double integrator[1].Such a controller is continuous and consequently is free of jumping switch.In a recentwork[2],a class of saturated fnite-time stabilizers are presented for multiple integrators and a skillful analysis method was proposed for verifying the saturation reduction.

Constructing fnite-time stabilizers for compensating input delays is a signifcantissue.In this line,profound results were achieved in[3]by means of time-varying distributed delay feedback;with the aid of the so-called Artstein’s transformation[4],the mentioned problem has been reduced to solely assigning a fnite-time stabilizer[5].

In addition,the stabilization design for compensating input saturation and input delays has long occupied the attention of the control community.In most cases,the kernel technical work is to verify the reduction ofsaturated terms by fully using suitable normalforms,Newton-Leibniz formula and Lyapunov functional(see for instance[6]-[9]).

However,there is currently no fnite-time stabilizing design that compensates both input saturation and input delays.The algorithms in[6]-[9]do not take into account the fnitetime stability and the classical time-optimal control design;the works in[1],[2]do not consider delay compensation;and the works in[3],[5]do not deal with input saturation.Therefore,it will be an important theoretical work to design fnite-time controllers that compensate both input saturation and inputdelay.

Moreover,exploration in this direction is of practicalsignificance.As we know,the bounded bang-bang controlcan bring about fnite-time stability and the shortest transition time,but cannot allow a time delay.In fact,a delay in the input will make it diffcult to achieve the prescribed performance and even give rise to serious consequences.For example,when the inputis subjectto a time delay,itmay happen thata spacecraft has a downward velocity while it lands on the ground.

Due to the above observations,for a double integrator we would like to presenta fnite-time stabilizer thatcompensates both input saturation and input delay.The detailed technical works are stated as follows:

1)With the aid of the Artstein’s transformation[4]and the reduction approach in[5],the problem under consideration is reduced to assigning a saturated fnite-time stabilizer.This will largely simplify the design/analysis,for there is no need to deal with delayed terms when we focus on the equivalent system.

2)The saturated fnite-time stabilizer is motivated by the method in[2].As we know,itis hard to verify the saturation reduction in a cancellation way,for there is no suitable normal form due to fractionalexponents.To this end,we will suggest a saturation reduction analysis method that slightly differs from the one in[2].Specifcally,we do not compute small time intervals for contradictions,but compute the derivatives of saturation functions in small domains and prove that the related derivatives are non-positive.Once the saturated controller reduces to a linear one,we invoke the homogeneity based stability theory[1]to analyze the fnite-time stability of the reduced system.These efforts allow us to obtain a saturated fnite-time stabilizer that can get rid of abs(·)and sign(·)functions.

3)In addition,we will show that,in the case of the double integrator,the fnal control design has a simple form in the sense that it does not contain integralterms.

The rest of the note is organized as follows.In Section II,we present the problem formulation and give mathematical preliminaries.In Section III,we provide the controldesign and stability analysis.Simulations are also given in this section to illustrate the effectiveness of the design.In Section IV,we make comments on the work in this note,emphasizing the importance of suitable methods and pointing out a potential extension.Finally,concluding remarks are put into Section V.

II.PROBLEM FORMULATION AND PRELIMINARIES

A.Problem Formulation

The bang-bang time-optimal controller is bounded and can guarantee the fnite-time stability and the shortestconvergence time.In the following,we will show that an inputdelay will lead to a serious consequence.

Consider the system

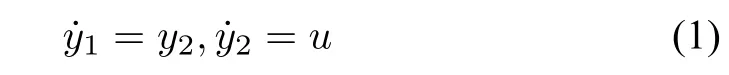
and fnd a suitable control u(|u|≤1)to minimize J=dt=Tf.Invoking[10],one knows that under the initial condition y1(0)=y2(0)=1,the bang-bang control law is described by

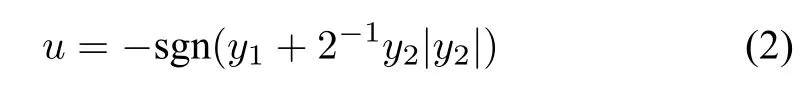
and the shortest transition time Tf=1+√6 can be calculated directly.

We now suppose that u is subjectto an inputdelay,namely,we will focus on a system like

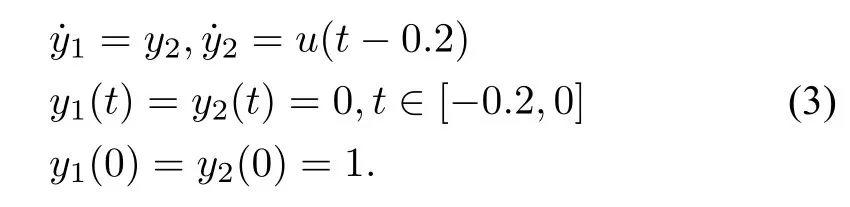
If one simply uses the following controller:

the histories of states and inputwill exhibitas follows.

Fig.1. Histories of states and input of system(1),(4).

From Fig.1,it is observed that when y1reaches zero,y2takes a negative value.If system(1)represents the motion of a landing spacecraft,simulations in Fig.1 show that the spacecraft bumps into the ground.Namely,some serious consequences will be brought about,once the time-optimal controller is subject to a time delay.Therefore,it would be theoretically and practically signifcantto develop a fnite-time stabilization algorithm for compensating both input saturation and input delay;which is exactly what this note addresses.

B.Preliminaries

We frst recall the Artstein’s transformation and its application in fnite-time stabilization of systems subject to input delay(for details the reader is referred to[4],[5]).

Consider the system subject to an inputdelay h

Making the Artstein’s transformation

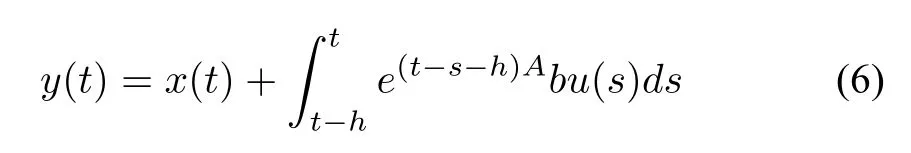
system(5)is transformed into

Noting

the transformation(6)is the same as that in[5],where the Artstein’s transformation is described by

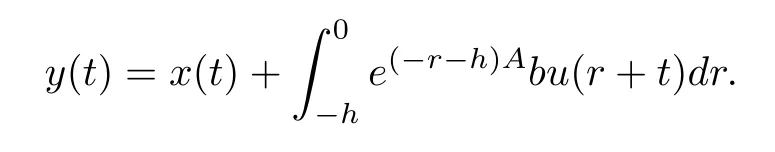
From Theorem 7 of[5],we have

Lemma 1:If system(7)is fnite-time stabilizable by a feedback control

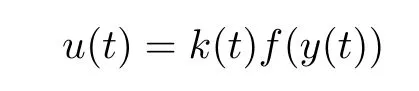
with k(t)bounded and f:Rn→R continuous such that f(0)=0 and there is a strictly increasing functionαsuch that

then,system(5)is fnite-time stabilizable by the feedback

We then recall homogeneity concepts and a related lemma from[11].Defne the dilationΔk(x1,...,x2)=(kr1x1,...,krnxn),k＞0,where x1,...,xnare suitable coordinates on Rnand r1,...,rnare positive real numbers.

Def nition 1:With respect to the dilationΔk(x1,...,x2),a vector feld F is homogeneous of degree m if and only if the i th component Fiis homogeneous of degree ri+m.

Lemma 2:The origin is a fnite-time stable equilibrium of F ifand only ifthe origin is an asymptotically stable equilibrium of F and m＜0.

This criterion willfacilitate the fnite-time stability analysis.Next,we introduce useful inequalities[12]:

1)For a constant p(a ratio of positive odd integers)and for any x,y∈R,the following inequalities hold:

2)Let c and d be positive constants.Given any positive number r＞0,the following inequality holds:

Finally,the saturation level function is defned as

satε(s)=sign(s)min{|s|,ε},s ∈ R,ε＞ 0.

III.CONTROL DESIGN AND STABILITY ANALYSIS

Consider the double integrator that is subject to an input delay h:

By making an Artsteins transformation

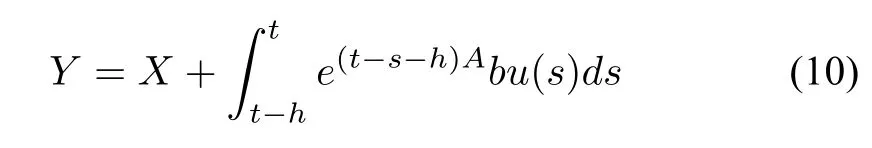
system(9)is described by

where

Making another transformation

we then have

In this note,we will frst present a saturated fnite-time stabilizer for system(13),and then use Lemma 1 to show that,after substituting variables,this controller will be a globally fnite-time stabilizer of system(9).

A.Saturated Finite-time Stabilizer of System(13)

We willfrstfocus on system(13),for which the following saturated controller is assigned:

where

and the control parameters bi(i=1,2)will be determined later.

Remark 1:In[1],the saturated fnite-time stabilizer for system(13)is described by

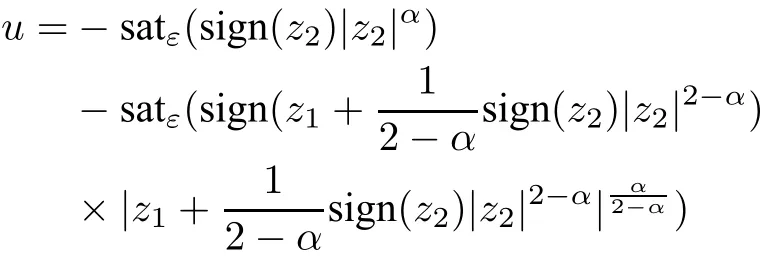
with α ∈ (0,1),ε＞ 0.Getting rid of functions sign(·)and|·|,here we willachieve a new saturated fnite-time stabilizer.

In the following,we show that the controller(14)is a fnite-time stabilizer of system(13)under suitable parameter conditions.

Red uction Analysis o f S aturated Terms:

Fact 1:The controller(14)of system(13)reduces to an unsaturated one in a fnite time under the following parameter conditions:

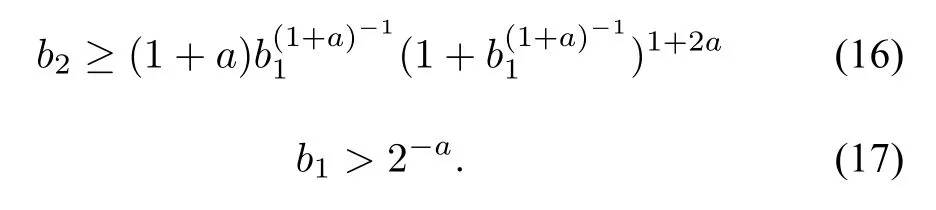
Proo f:We prove this resultin a bottom-up recursive manner.

Step 1:Consider the z2subsystem and suppose that≥ εholds for all t≥ 0.There holds

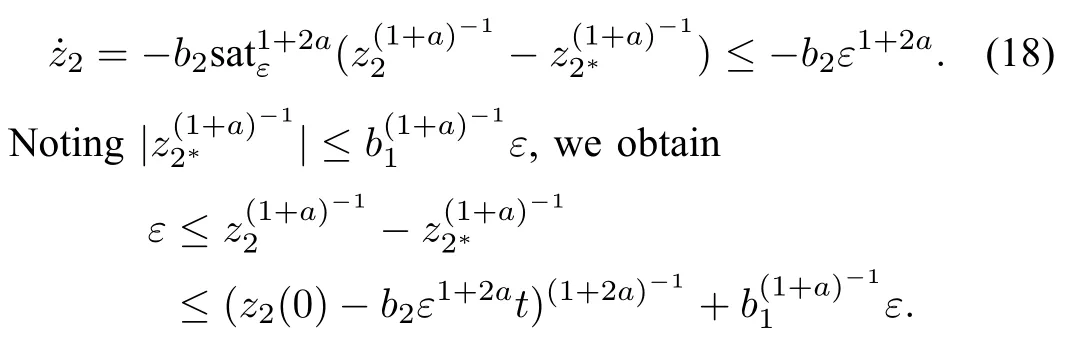
As time goes to infnity,we obtain a contradiction

So there exists a fnite time t2such that

We then calculate the time derivative ofat the time instant t2.By(15),we havetogether with(19),we obtain

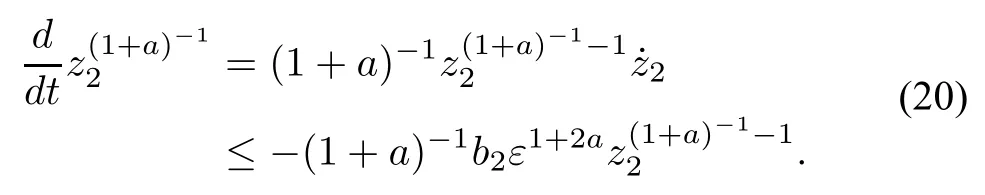
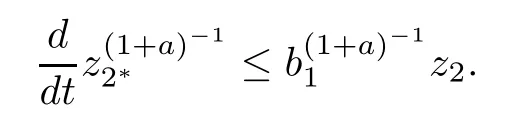
From(19),we have

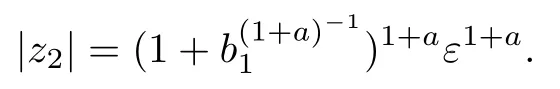
For cancellation,we calculate|z2|in the following way:

Then,the parameter condition(16)leads to

Namely,we have

Combining(19)and(22),we have

Similarly,it can be shown that there exists a time t1such that

Step 2:We claim that with b1＞2-a,there exists a fnite time t1(≥ T2=max{t2,})such that z1(t)≤ εholds for all t≥t2.In fact,using(23),(24)and(F1),we frst have|z2-z2∗| ≤ 2-aε1+a;next,for z1≥ ε,we have z2∗ =-b1ε1+a.Hence,by(17),for z1≥ εthere holds

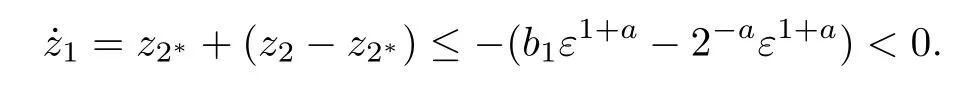
This implies that the claim is true.

Likewise,it can be shown that a fnite time(≥T2)exists such that z1(t)≥ εholds for all t≥. ■

Asymptotical Stability Analysis of the Reduced System:

After the time T1=max{t1,,the controller(14)is reduced to

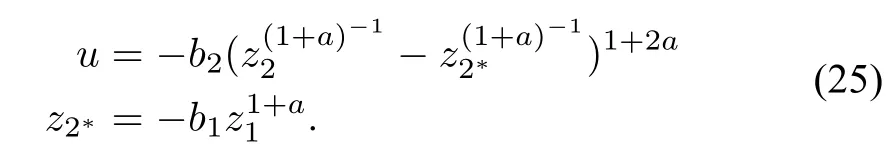
Following the backstepping method in[12],we can prove:

Fact 2:There are suitable b1,b2such that system(13)with the controller(25)is fnite-time stable.

Proo f:Fact 2 is proved in three steps.

Step 1:Defne the function W1=(2-a)-1for the subsystem=z2.Keeping(25)in mind,we obtain

where l＞0 is tunable.

Step 2:For the whole system(13),(25),we defne the function

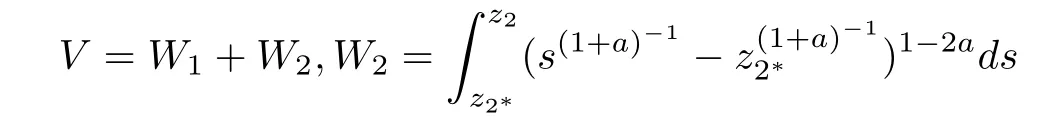
and have

To calculate(∂W2/∂z1)z2,we obtain

Next,there holds

We then have

where m is a tunable positive constant.Noting u=-,we fnally have

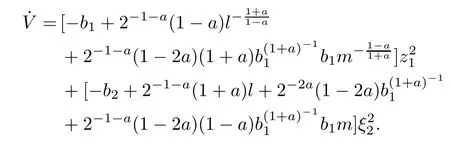
Direct computations show that,with

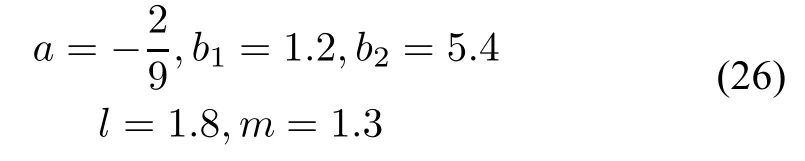
Finite-time Stab ility Analysis:

Combining Facts 1 and 2,we know that the closed-loop system(13),(14)is globally attractive and locally asymptotically stable,while also globally asymptotically stable at the origin in terms of[13].

Moreover,we can claim that the reduced system is fnite-time stable.At frst,we show that system(13),(25)is homogeneous of order a with respect to the dilationSince z2and u=are homogeneous of degree 1+a and 1+2a,respectively,it follows from Defnition 1 that the vector feld

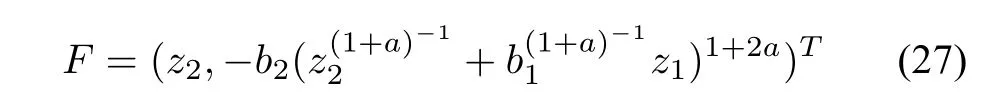
is homogeneous of order a.

By a＜0 and Lemma 2,the claim is true.

Thus,for system(13)we have actually constructed a globally fnite-time stabilizing controller,since system(13),(14)is globally asymptotically stable at the origin and in a fnite time the states enter a small domain

in which system(13),(14)is fnite-time stable.

So far we can have the following result:

Proposition 1:The controller(14)is a saturated fnite-time stabilizer of system(13)if the parameter conditions(16),(17)and(26)are fulflled.

Remark 2:The saturated fnite-time stabilizer for system(13)is motivated by the method in[2].A slight modifcation to the method in[2]is used:instead of calculating smalltime intervals for contradiction,we verify the saturation reduction in such a way that the derivatives of saturation functions are calculated in small domains and are proved to be non-positive(see the Proof of Fact 1).

B.Saturated Finite-time Stabilizer of System(9)

In this part,we give the entire expression of the saturated fnite-time stabilizer for system(9).

We frst give a candidate of controller(14)by computing parameters a,b1and b2.Let a=-2/9;set b1=1.2,b2=1.6 according to(17)and(16)of Fact1;assign b1=1.2,b2=5.4 according to(26)of Fact 2.So we fnally set

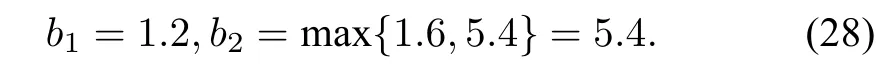
Now a saturated fnite-time stabilizer of system(13)is described by

We then invoke Lemma 1 to show that,based on the controller(29),one can have a saturated fnite-time stabilizer of(9).

Since z1and z2are proved to be bounded and there holds(1+a)-1＞1,there is a certain d＞0 such that

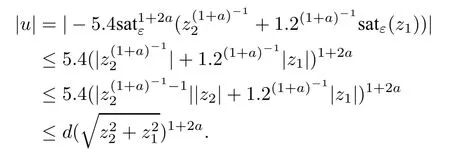
Namely,the condition(8)of Lemma 1 is fulflled.Next,ithas been proved that the controller(29)is a fnite-time stabilizer of system(13).Thus,by Lemma 1,(12)and(29),we obtain a saturated fnite-time stabilizer of system(9):

where Y1,Y2are given in(10).

Note that Y1,Y2contain integral terms and involve the history of the control signals.Interestingly,by further using equations in(9),the expression of the fnal controller will not include integral terms.

At frst,we have

Furthermore,from equations in(9),we have

Also,we have

Thus,there hold

Keeping in mind(30)and(31),we fnally obtain the entire expression of the saturated fnite-time stabilizer for system(9):

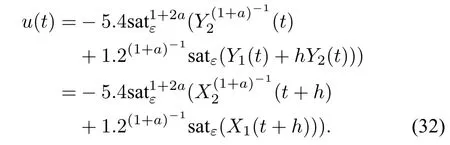
Moreover,due to time delay,the actual control action will be

In the end,the result in this note is summed up as follows.

Theorem 1:For a=-2/9 and any h,ε＞ 0,the controller(32)globally fnite-time stabilizes system(9)if the parameter conditions(16),(17)and(26)are fulflled.

Remark 3:In the case where the simple double integrator is considered,the fnalcontroldesign does notcontain an integral term.

In the following,we use numericalsimulations to show the effectiveness of the algorithm.

Take a=-2/9,ε=1,h=0.2.Run simulations for system(9),(32)under the initial conditions Simulations in Fig.2 show thatthe continuous controller(32)can guarantee that states converge to zero in fnite time,although the input is subject to a time delay.

Using the simulation example,we now explain that the causality requirementis met.

Fig.2. Histories of states and input of system(9),(32).

When t=0,the control action is taken as

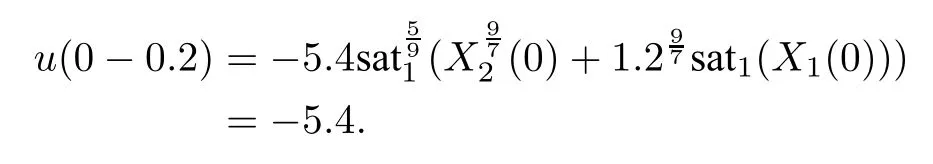
At this time instant,u(0-0.2)has an explicit value that is determined from(X1(0),X2(0))=(1,1).

When 0＜t≤0.2,the control action is taken as

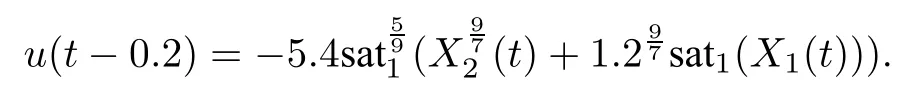
Clearly,in the time interval(0,0.2],u(t-0.2)can always be determined from the input value at the previous instant.Therefore,it is safe to say that the causality requirement is met.

Finally,it is noted that the controllers may be sensitive to input delay mismatches,since one needs to know the exact input delay when utilizing the suggested control design.Therefore,it would be a signifcant issue to address the robustness of such controllers.

IV.SOME DISCUSSIONS

In this section,we make some comments on the work in this note.

Firstly,we explain that searching for a suitable method is crucial to establish our algorithm.

To deal with the double integrator,we have made some attempts but ultimately failed.Then,we search for other solutions and fnd that the problem is largely simplifed once we jointly use the results in[2],[4]and[5].

1)By making the Artsteins transformation[4]and using the resultin[5],the concerned problem is reduced to how to obtain a saturated fnite-time stabilizer;

2)By drawing inspiration from[2],a saturated fnite-time stabilizer including no abs(·)and sign(·)functions can be explicitly constructed.

Two failed attempts are listed as follows.

Scheme 1:

system(9)is described by

By introducing the transformation

for which we assign the saturated control law:

where 0＜ε＜1,a=-2k1/(2k2+1),1≤k1＜k2,and multiplying coeffcients bi(i=1,2)are to be determined.

Transferring delay h into the perturbed termψ,we hope that the problem is simplifed and only the saturated fnitetime stabilization problem needs to be considered.Butwe fnd that the fnite-time stability of the reduced system is hard to prove.In fact,due to the perturbed termψand particularly the negative parameter a,itis hard to choose suitable bi(i=1,2)to ensure the fnite-time stability of the reduced system.A more detailed explanation is given as follows.Suppose that the saturation reduction is already verifed and there hold

and

Using the function W1=(2-a)-1for the x1subsystem of(33),and=-b1,we obtain

and here we need to specially focus on the term

Noting|ξ2|≤ ε＜ 1,if a ＞ 0 we will have

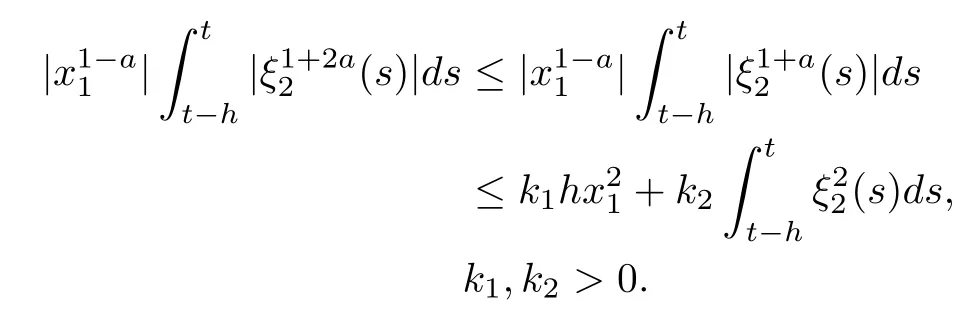
This estimate is useful for the stability analysis since we fnally hope to obtain the dissipative inequality with the form

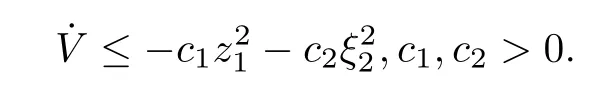
But we have to let a＜0 for fnite-time stability.Thus,if we make a computation in the following way

The term|xa|(|xa|≥ εa＞ 1)willbecome an obstacle to take suitable bi(i=1,2).Besides,other computational manners will give rise to the same problem.

Scheme 2:

Use the approach in[8]for system(9)and directly design

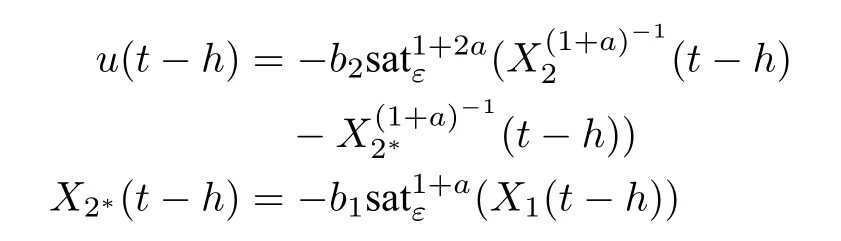
where 0＜ε＜1,a=-2k1/(2k2+1),1≤k1＜k2,the control parameters bi(i=1,2)are to be determined.

In this case,delayed terms need to be treated at each step of the saturation reduction analysis and some conservative estimates will be inevitable due to fractional exponents.At the same time,the delayed terms and the fractionalexponents will also make it diffcult to dealwith the reduced system.

Secondly,we briefy discuss a potential extension of the suggested algorithm.

Initialinvestigation shows itis possible to dealwith the n-th orderintegrator,since we can stillreduce the problem into how to assign saturated fnite-time stabilizers.As an example,letus consider the triple integrator that is subject to an input delay h:

By making the Artstein’s transformation

system(34)is described by

Making another transformation

we fnally have

Then,itsuffces to consider the saturated fnite-time stabilization of the equivalentsystem.

As it can be imagined,we will face a parameter assignment problem in the case of the n th order integrator.In fact,we now have to use the contradiction method in[2]to do the saturation reduction analysis.As a consequence,some multiplying coeffcients will become quite large as the system dimension increases.Likewise,the multiplying coeffcients needed in treating the reduced system will also be too large.

In addition,atpresent,itis notclear whether the algorithm can be extended to some feedforward nonlinear systems.Apart from the problem of choosing control parameters,we have to ensure that the equivalent system has an upper-triangular structure.Moreover,once the equivalentsystem contains some delayed terms,we will bump into the same problem as in Scheme 1.

V.CONCLUSION

Finite-time stabilization,compensation of input saturation,and compensation of input delay are important topics in the control community.In this note,through jointly using the existing approaches,we have for the frst time provided a fnite-time stabilizing design that compensates both input saturation and input delay.Hopefully,the analysis method in this note might motivate some new thinking.