Adaptive Neural Network-Based Control for a Class of Nonlinear Pure-Feedback Systems With Time-Varying Full State Constraints

Tingting Gao,Yan-Jun Liu,Senior Member,IEEE,Lei Liu,and Dapeng Li

Abstract—In this paper,an adaptive neural network(NN)control approach is proposed for nonlinear pure-feedback systems with time-varying full state constraints.The pure-feedback systems of this paper are assumed to possess nonlinear function uncertainties.By using the mean value theorem,pure-feedback systems can be transformed into strict feedback forms.For the newly generated systems,NNs are employed to approximate unknown items.Based on the adaptive control scheme and backstepping algorithm,an intelligent controller is designed.At the same time,time-varying Barrier Lyapunov functions(BLFs)with error variables are adopted to avoid violating full state constraints in every step of the backstepping design.All closedloop signals are uniformly ultimately bounded and the output tracking error converges to the neighborhood of zero,which can be verified by using the Lyapunov stability theorem.Two simulation examples reveal the performance of the adaptive NN control approach.

I.INTRODUCTION

I Nrecent decades,the control problems of various nonlinear systems have received wide attention.In the initial stage,scholars often used matching conditions to derive the asymptotic stability of systems.With the continuous progress of nonlinear systems control technology,the limitations of matching conditions have restricted furtherresearch of systems control.To overcome this problem,the backstepping technique has been introduced.This approach reduces the difficulty of the problem with decomposition of the systems to achieve control purposes.Over the past two decades,there has been an increased interest in adaptive control technology because it is a very effective toolforhandling systems with uncertainties.In[1],the adaptive dynamic programming algorithm was successfully applied to a discrete-time optimalcontrolscheme.The backstepping technique was used in[2]and[3]to achieve a significant breakthrough in the adaptive control of a nonlinear time-delay system and nonlinear stochastic jump system.On the other hand,the backstepping method was also applied to nonlinear strict feedback systems[4]-[8]with unknown items.After obtaining a series of research results in strict feedback systems,researchers began to study corresponding nonlinear pure-feedback systems.In[9],an uncertain purefeedback nonlinear system is transformed into a non-affine form,and an adaptive control method was designed to solve the global asymptotic state stabilization problem.In modern controltheory,neural networks(NNs)have been developed as approximators of unknown nonlinear functions.The work in[10]and[11]developed an adaptive dynamic programming algorithms with a value iteration and local value iteration for optimal control of discrete-time nonlinear systems,while NNs were proposed to solve the problems faced by unknown items.For a nonlinear pure-feedback system[12],based on the idea of backstepping,the author used the implicit function theorem to assert the existence of continuous desired virtual controls,and NNs were adopted to approximate the controllers.Adaptive NN control schemes were used on a class of output feedback nonlinear systems[13]-[16]with unknown functions.On accountofbackstepping algorithm and the Lyapunov method,adaptive NN approximation techniques were proposed in[17]-[19]forthe ocean vessels,novelcoaxial eight-rotor unmanned aerial vehicles and networked multiagent systems,while their effectiveness have been proven.In addition,[20]-[33]also proposed an adaptive NN control design method for nonlinear systems.In fact,due to the physicallimitations ofthe controlleras wellas the mechanical design and manufacture in the actual systems,various types of constraint characteristics exist in many typical industrial controlsystems.However,the system’s constraints are ignored in these papers.

Underthe influence ofthe actualbackground,the theoretical study of constraints becomes more and more important.In nonlinear control system[34]based on predictive control,the problem of satisfying pointwise-in time input and/or state hard constraints was studied,and predictive control has also been applied in[35].The controlstrategies of non-holonomic mechanicalsystems under various constraints were studied in[36].Constraints can be roughly divided into the following types:output constraints,partial state constraints,full state constraints,etc.In many controlapplications,there are strong constraints on the control and state variables.For constrained systems,designing controllers based on unconstrained conditions willdeteriorate the stability of the systems,produce some undesired responses such as oscillations,and even destroy the hardware equipment of systems.BLF is now a widely used approach to control constraints in design.In[37]-[46],the adaptive control method for nonlinear systems with output constraints and state constraints were investigated based on BLF.The adaptive control design based on a BLF framework notonly can dealwith the uncertainty of parameters,butalso can deal with the uncertainty of functions by using NNs.The adaptive NN control design in[47]-[53]were applied to the BLF-based nonlinear systems with output or state constraints.The actual systems,state parameters and control parameters are time-varying and determined by the physicalcharacteristics ofthe restraintsystems,so the modelcannotbe described with the usualparameters.To dealwith the aforementioned control problems ofthe systems,both the systems time-varying model and systems constraints mustbe taken into account.Motivated by these advancements in the constraints,many time-varying output constraints have been studied for various nonlinear systems[54]-[56].In view of adaptive NN tracking control technology,state constraints are considered in nonlinear timevarying systems[57]-[59].Based on the above theories,the authors applied time-varying state constraints to a robotsystem[60]and DC motorsystem[61],respectively.However,there is no work to dealwith the adaptive NN controlofpure-feedback systems with time-varying constraints,which motivates our study.

Motivated by the aforementioned observations,we pay close attention to the problem of adaptive NN tracking control scheme for uncertain nonlinear pure-feedback systems with time-varying full state constraints in this paper.The main contributions can be described as follows:

1)Many actual systems can be described as pure-feedback systems.Meanwhile,control parameters are time-varying and determined by the physical characteristics in the actual systems.However,as far as we know,the control of purefeedback systems with time-varying state constraints are rarely mentioned in the literature.

2)For the sake of control of pure-feedback systems,the implicit function theorem is employed to assert the existence of the smooth ideal control input.At the same time,NNs are applied to estimate both the virtual and actual controllers.Then,the mean value theorem is used to convertpure-feedback systems to strict feedback systems.

3)Aimed at transformed systems,the BLFs are employed to ensure that the full state constraints were not violated in any step of backstepping design.

Furthermore,to obtain the stability of the pure-feedback systems,a significant theorem is given and proved.The feasibility of the designed controller can be proved though two simulation examples.functions

II.SYSTEM DESCRIPTIONS

Consider nonlinear pure-feedback systems with the following form:

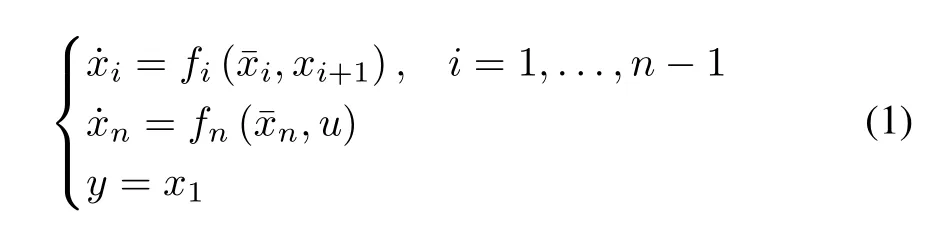
The control objective of this paper is to construct an adaptive feedback controller u which ensures that the system output y is tracks the reference signal yd,while allthe closedloop signals are uniformly ultimately bounded and the timevarying full state constraints are not violated.

Remark 1:In this paper,nonlinear pure-feedback systems with state constraints are researched.Compared with the nonpure-feedback systems[40]-[46],pure-feedback systems have a wider range of applications as a class of more general lower triangular nonlinear systems.Moreover,in contrast to the control of nonlinear systems[40]-[46],[48]-[50]with constantstate constraints,time-varying state constraints can relax the conditions ofconstantones.Atthe same time,although[62]also addressed the pure-feedback systems with timevarying state constraints,linear parameterization is necessary.This paper is more general in the case that the function is completely unknown.

Assumption 1[60]:There exist the constants,i=1,...,n,j=0,1,...,nsuch that(t)≤and(t)≤k(t).,∀t≥ 0,where(t)denotes j th time derivative of Kci(t)

Assumption 2[55]:It is assumed that yd(t)satisfies|yd(t)|≤Y0(t)＜kci(t)and its i th time derivative(t),satisfy(t)|≤ Yi,i=1,...,n,∀t≥0,where Y0(t):R+→ R+and Y1,...,Ynare positive constants.

Lemma 1[12]:For∀(x,u)∈ Rn×R,assume that f(x,u):Rn×R→R is continuous differentiable,and there is a constant d such that＞d＞0.Then there exists a smooth function u∗=u(x)such that f(x,u∗)=0.

In this paper,for the systems(1),define unknown nonlineari=1,...,n-1 and

Assumption 3[12]:The signs of functions gi(·),i=1,...,n are bounded,i.e.,there existthe constants≥gi＞0 such that gi≤|gi(·)|≤.Without loss of generality,this paper assumes that gi≤gi(·)≤.

In[12],the radial basis function(RBF)NNs are employed to approximate the unknown nonlinear functionΨ(Y):Rl→R as follows:

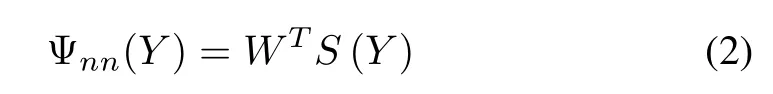
where Y∈ΩY⊂Rl,W=[w1,w2,...,wm]T∈Rm,and m are the inputvector,the weightvectorand the node number m＞1 of the NNs,respectively;while S(Y)=[s1(Y),s2(Y),...,sm(Y)]T,where si(Y)being defined as the commonly used Gaussian functions,the form defined as

where εiis the width of the Gaussian function and τi=[τi1,τi2,...,τil]Tis the center of the receptive field.

It has been shown that any smooth function in a compact setΩY⊂Rlcan be approximated by (2) to arbitrary accuracy as

whereηis the approximation error andW∗is the optimal weight vector which is constructed as the value of Wthat minimizes|η|forallY ∈ ΩY⊂ Rl,i.e.,

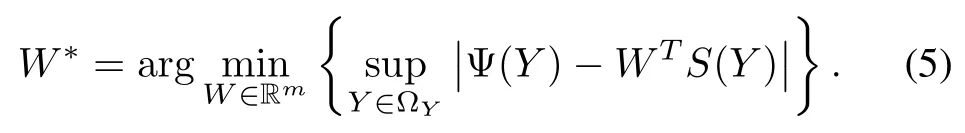
According to Assumption3,wehave＞gi＞0 foralli+1∈Ri+1.Introducethefunctionφias

whereki,i=1,2,...,n are positive constants, and define the tracking errorz1=x1-ydand the variables zi=xi-αi-1,i=2,...,n,whereαi-1is a virtual controller to be designed by Stepi-1 of the backstepping method.Because=0,the following inequality holds:

Using Lemma 1 which is an implicit function theorem obtained from[12],withxi+1,i=1,...,n-1andu as virtual control input, for every value of,i=1,...,nand φi,i=1,...,n,there exists the smooth ideal control inputs(,φi),i=1,...,n,suchthat

Combining the mean value theorem, there existλi∈ (0,1)that makes

Lemma2[61]:For anykbiandzi,i= 1,2,...,n,satisfying|zi|＜kbi,then there iswherekbiwill be given later.

Proof:For anyzithat satisfies|zi|＜kbi,the term log(/(-))in(10)can be rewritten as

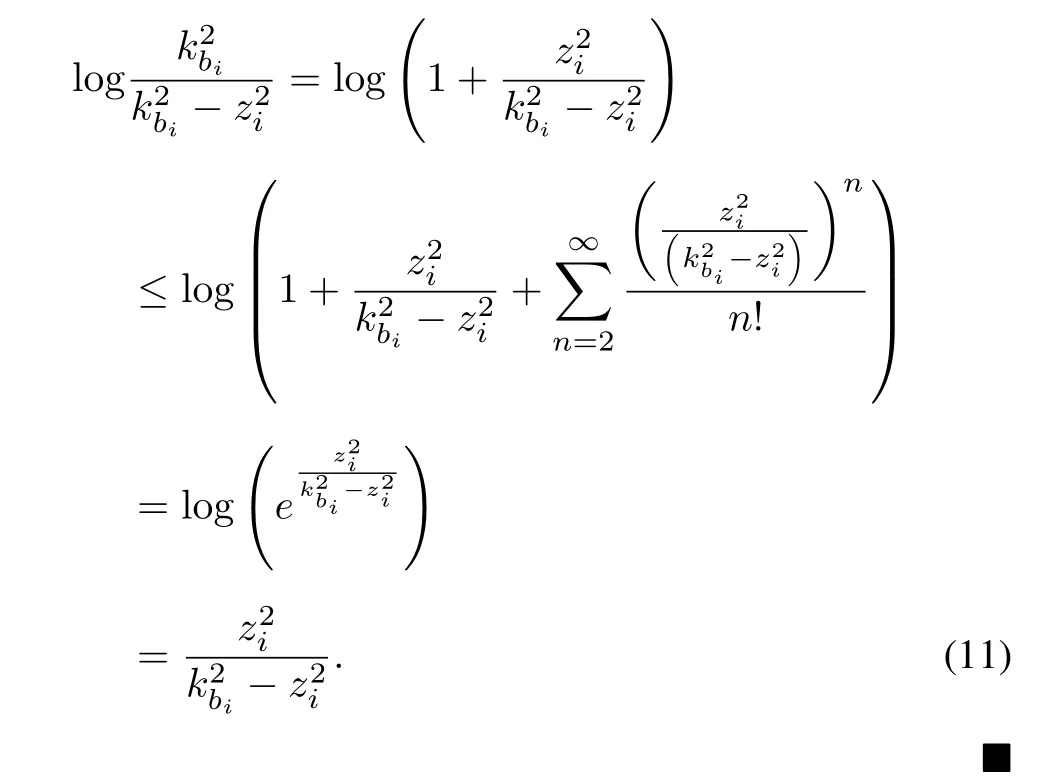
Young’sInequality: It is assumed that if ∈ Rn,y ∈ Rn,p,q＞1and a is an arbitrary positive constant,and1/p+1/q=1,then

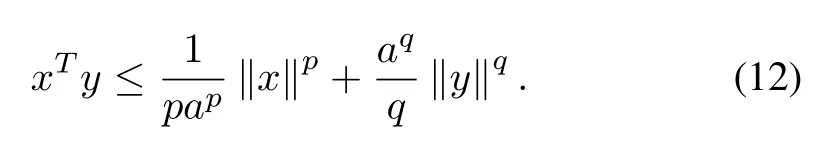
Especially,ifp=q=2,a is an arbitrary positive constant,,then

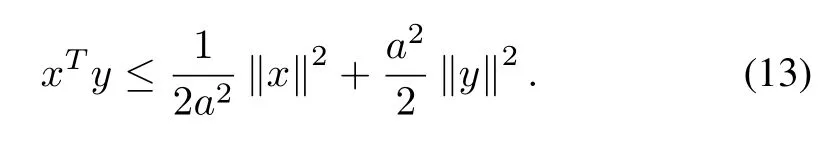
III.THE CONTROLLER DESIGN AND STABILITY ANALYSIS

In this paper, based on the backstepping method, an adaptivecontroller is designed for the nonlinear pure-feedback systemswith time-varying full state constraints. The specific processis as follows.

Based on the systems (1), we know that differentiating z1with respect to time yields

Substituting(6),(8)and(9)in to(14)yields

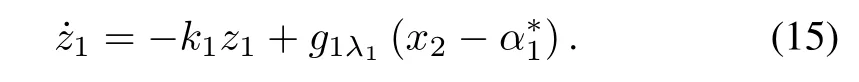
By defining the error variable2=x2-α1,we ex press

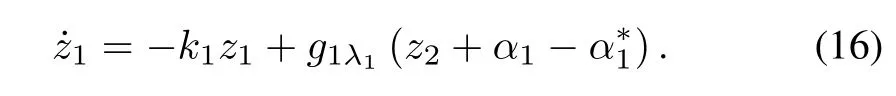
Consider the following positive definite time-varying Lyapunovfunction

where log(Δ)represents the natural logarithm ofΔ,=-,Γ1=＞0 is a constant gain matrix,andkb1(t)=kc1(t)-yd(t)is a barrier function.

Based on the definition of kb1(t),aand using Assumptions 1 and2,we can obtainkb1(t)≤Kb1withKb1being a constant.

Substituting (16) into the time derivative of V1leadsto

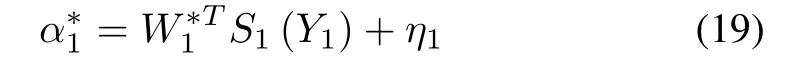
Design the virtual controlα1as

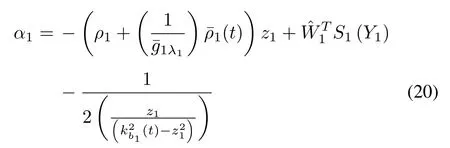
Substituting(19)and(20)into(18),on account of the fact that(t)+(t)/kb1(t)≥0,(18)can be further rewritten as

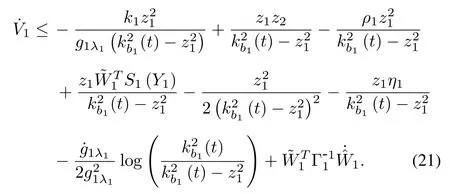
From Young’s inequality,it follows that

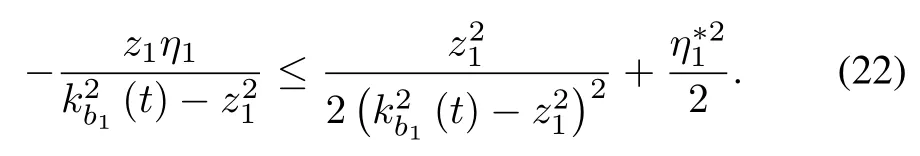
Further,(21)can be rewritten as

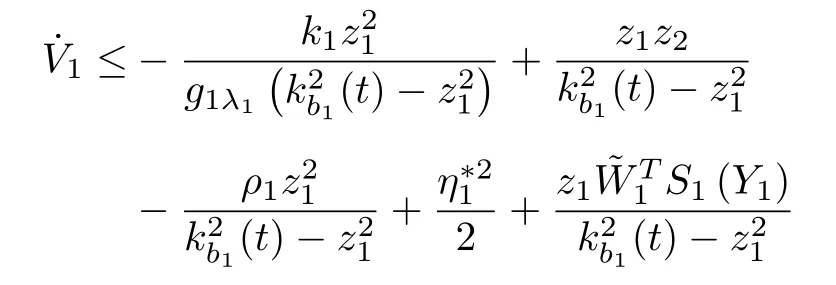
The adaptive law is designed as follows:

whereσ1＞ 0 is a design constant,andσ1-modification term σ1is used to improve the robustness when there is an NN approximation errorη1.

Using Lemma 2,the following inequality is obtained

Step i,2≤i≤n-1:Based on the systems(1),the time derivative of variable zi=xi-αi-1is

Substituting(6),(8)and(9)into(26)yields

By defining the error variable zi+1=xi+1-αi,we express

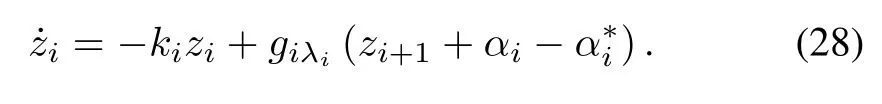
Becauseαi-1is the function of,yd,kbi-1,and,...,,˙αi-1can be described as

For simplicity,the following definition is given

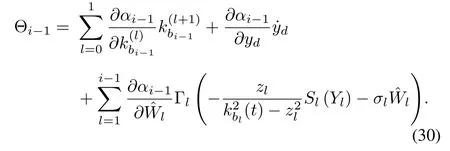
Consider the time-varying Lyapunov function candidate

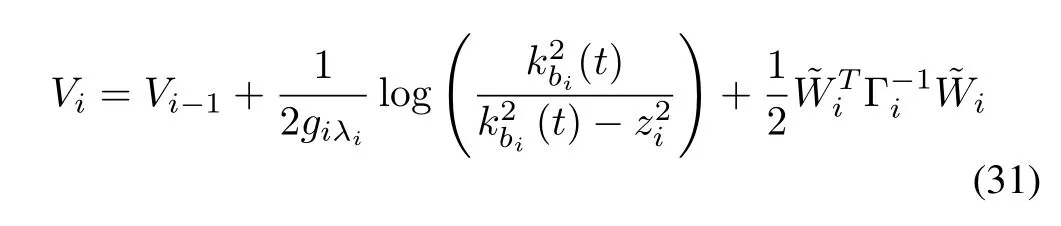
Substituting(28)into the time derivative of Vileads to

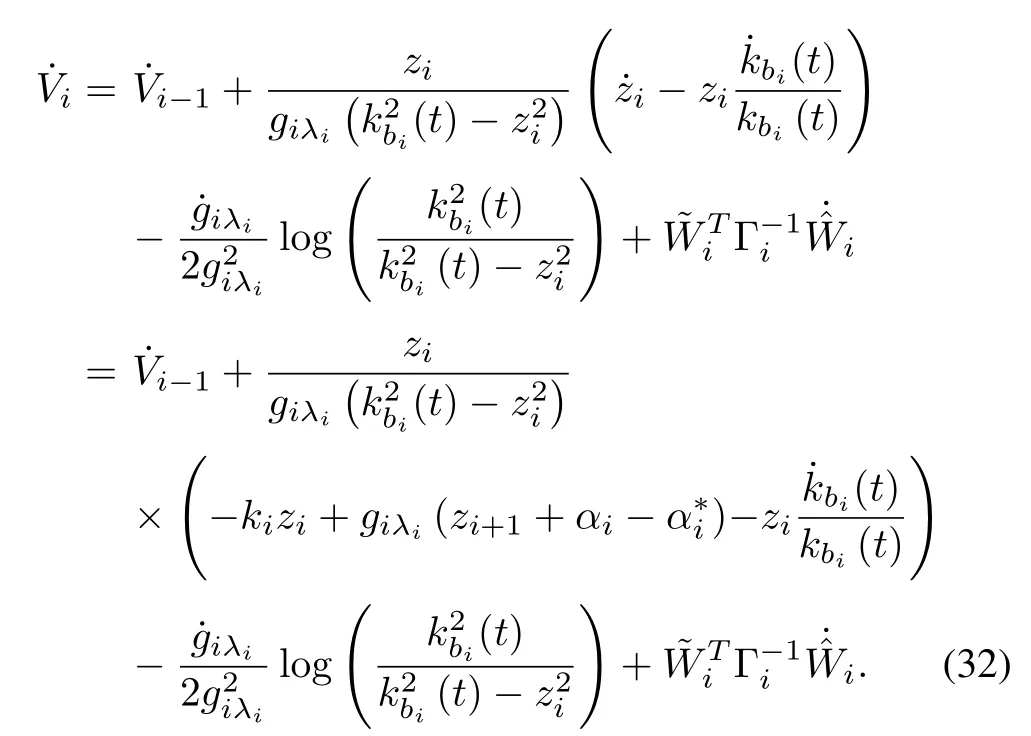
where approximation error|ηi|≤with constant＞0.

The virtual controlαiis designed as

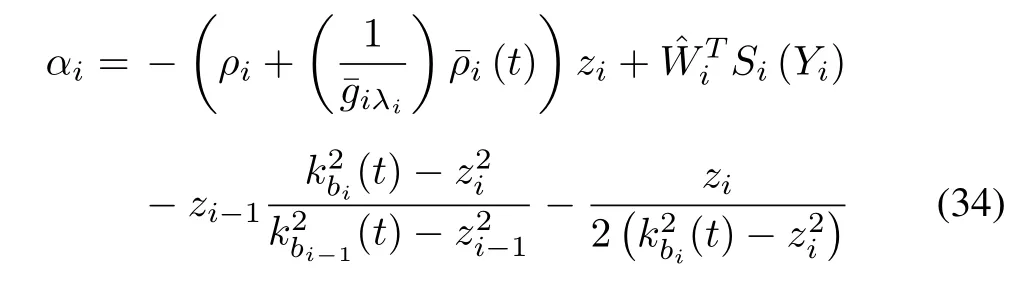
where design constantρi＞0 and the definition of(t)is similar to(t)in Step 1.

Substituting(33)and(34)into(32),and due to the factthat(t)+(t)/kbi(t)≥0,then(32)can be described as

Using Young’s inequality yields

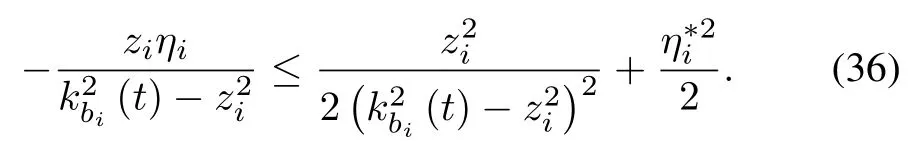
Further,(35)becomes

where σiis a positive constant,and σi-modification term σiis used to improve the robustness when there is a NN approximation errorηi.

Using Lemma 2,the following inequality is obtained:

Step n:In the laststep ofbackstepping,the actualcontroller u will be obtained.The time derivative of zn=xn-αn-1can be written as

Substituting(6),(8)and(9)into(40)yields

Becauseαn-1is the function of,yd,kbn-1,and,...,,the derivative ofαn-1obtain

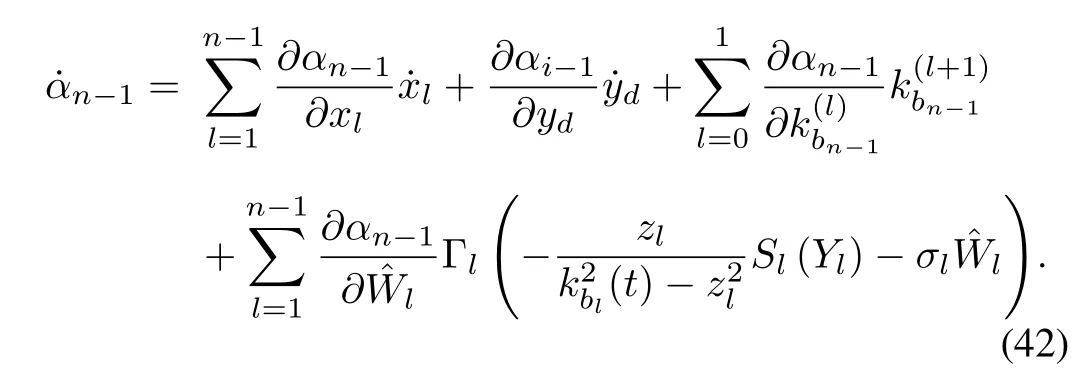
For simplicity,the following definition is given

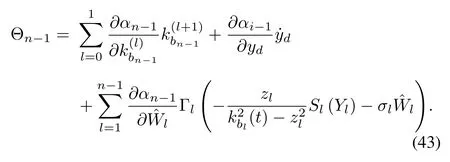
Consider the following positive definite time-varying Lyapunov function

Substituting(41)into the time derivative of Vnleads to

where|ηn|≤with constant＞0.

The following actual controller u is constructed:

where design constantρn＞0 the definition of(t)is similar to(t)in the Step 1.

Substituting(46)and(47)into(45),and based on the situation that(t)+(t)/kbn(t)≥0,while(45)can be further expressed as

Based on the following inequality:

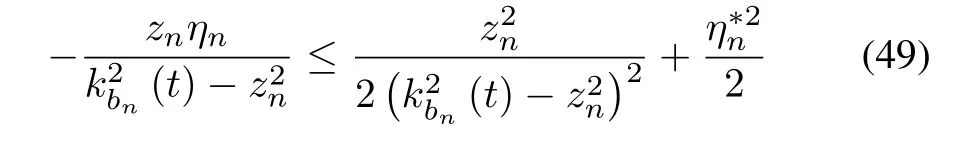
(48)can be computed as follows:

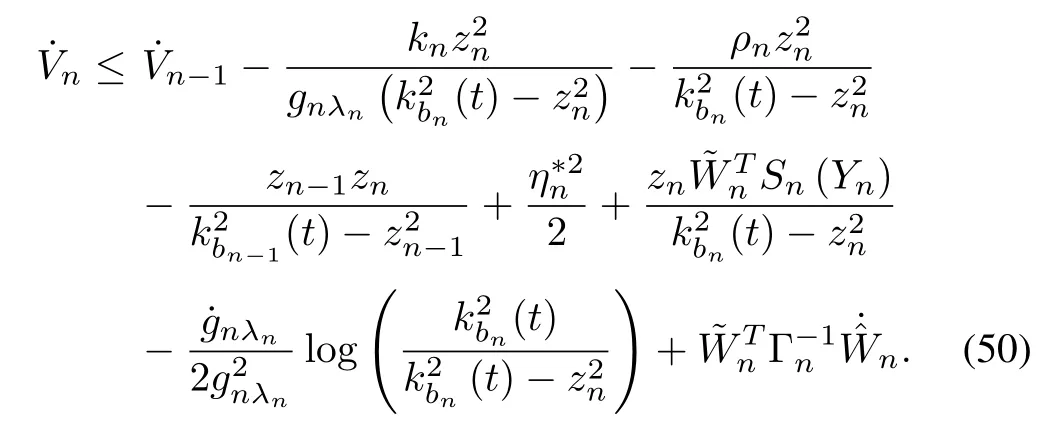
whereσn＞ 0 is a design constant,andσn-modification term σnis used to improve the robustness when there is an NN approximation errorηn.

Using Lemma 2,the following inequality is obtained:

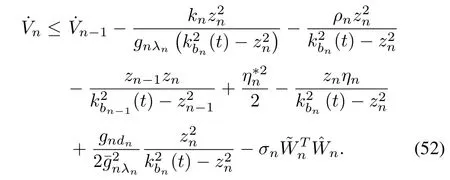
With the first n-1 steps,we have

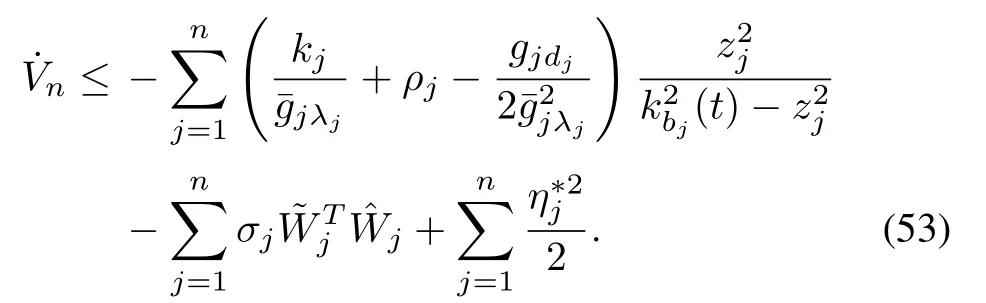
The following inequalities hold:

By selecting the suitable ρj,the inequality(= ρj+kj/＞0 is established.Then,we obtain

Combining Assumption 3,Lemma 2 with the above inequality,we can get the following inequality

Theorem 1:Under Assumptions 1-3,consider the systems(1)with time-varying fullstate constraints.If the initialstates|xj(0)|＜,j=1,2,...,n are satisfied,then the following properties can be guaranteed:the error variables zj,j=1,2,...,n are bounded;the time-varying full state constraints are never violated;and all closed-loop signals are bounded.

Proof:According to(17),(31)and(44),we have By choosing thewhere≥ τ/,andρj≥ τ/-whereτ＞0 is a constant.Then,there is the inequalityσj≥ τλmax{}by selectingτandσj.The derivative of Vnalong(56)and(57)satisfies

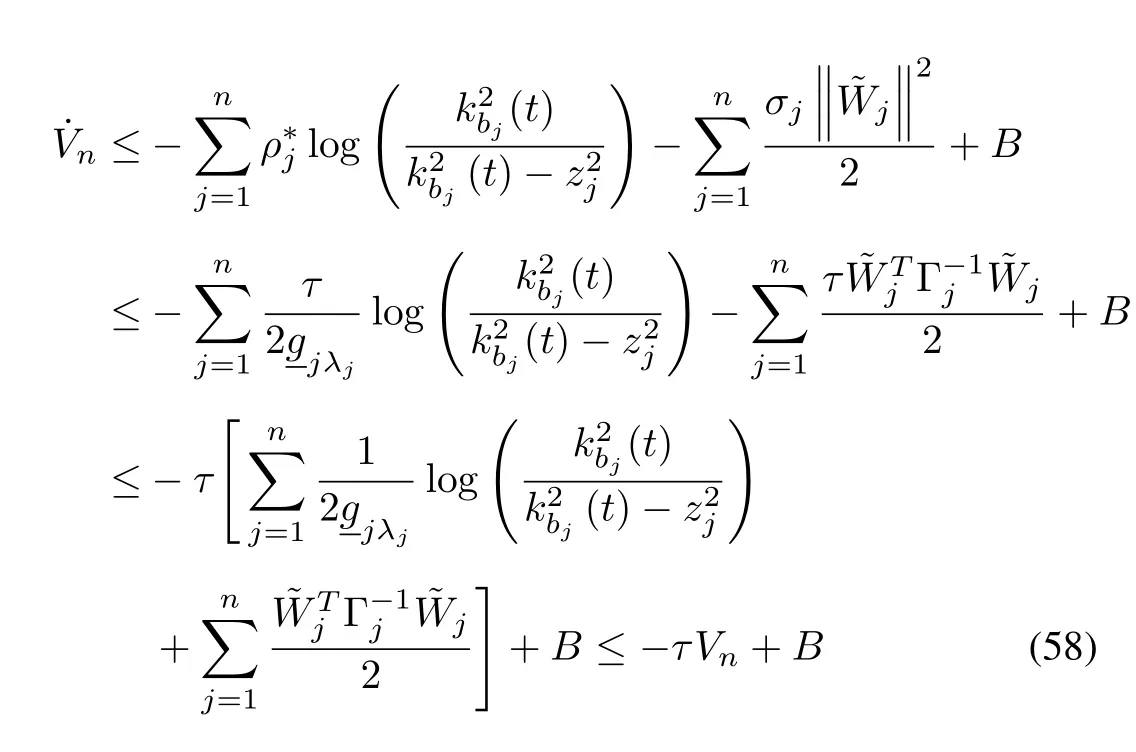
where

According to Lemma 2,|yd(t)|≤Y0and the fact x1=z1+yd(t),we have an inequality|x1|≤ |z1|+|yd(t)|＜ kb1(t)+Y0.Then we have|x1|≤kc1,where kc1(t)=kb1(t)+Y0.Further,there is|y|=|x1|≤kc1.Thus,the output signal is bounded.Itis obvious thatthe virtualcontroller which is defined in(20)is bounded|α1|≤1.From the fact that x2=z2+α1and Lemma 2,itfollows that|x2|≤|z2|+|α1|≤kb2+1.So,|x2|≤kc2,where kc2(t)=kb2(t)+1.Similarly,we can prove that|xi+1|≤,i=2,...,n-1,where(t)=kbi+1(t)+.Based on(60),wep can get()Hence,the states xj,j=1,2,...,n,the adaptive laws,j=1,2,...,n and the controller u are bounded.In view of the above analysis,we can determine that all signals in the closed-loop systems are bounded and the time-varying fullstate constraints are never violated. ■

Multiplying eτtby both sides of(58)yields

Integrating(59)over[0,t],which leads to

Combining(57)with(60),the following inequality can be obtained

where g∗=max1≤j≤n{jλj}.And taking the e-exponential of both sides of(61),we have

Then we can get the tracking error which satisfies

IV.SIMULATION EXAMPLE

In this section,two simulation studies are raised to demonstrate the effectiveness of the proposed adaptive NN control scheme in this paper.

Example 1:Consider the third order pure-feedback system

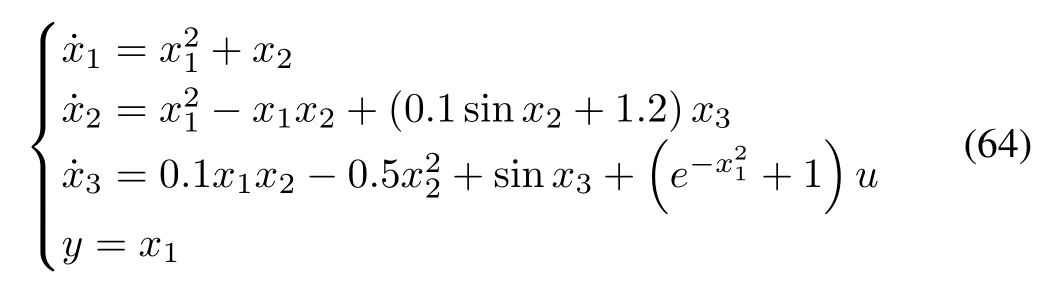
where the states of system are constrained in|x1|＜kc1=1.4+0.2 sin(0.5t),|x2|＜ kc2=2.6+0.6 sin(t)and|x3|＜ kc3=5+0.8 sin(t),the desired trajectory yd=0.8 sin(2t),and the virtual controllers and the actual controller are designed as

while the adaptation laws are designed as

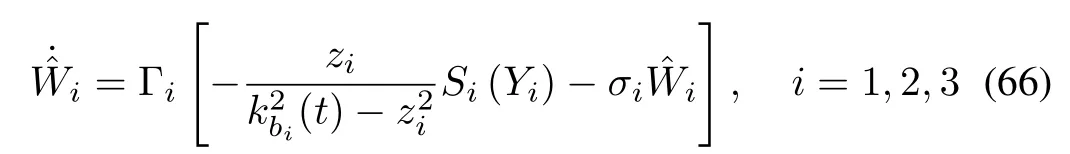
where

The initialconditions of the system are defined as x1(0)=0,x2(0)=1.4,and x3(0)=0,while the design parameters are given as followsρ1=40,ρ2=15,ρ3=18,1λ1=0.4,2λ2=0.5,3λ3=0.6,Γ1=7,Γ2=8,Γ3=4,σ1=0.6,σ2=0.5,σ3=0.4,β1=6,β2=7 and β3=9.

Figs.1-4 are the simulation results of system(64).Fig.1 clearly illustrates the excellent tracking performance of the system.At the same time,Figs.1 and 2 are given to descript the trajectory of state and error variables,respectively,and itis easy to see that the time-varying constraints are not violated.The trajectories of the adaptive laws and actualcontroller are displayed in Figs.3 and 4.From the above Figures,it can be concluded thatallclosed-loop signals remain bounded and the time-varying constraints are never violated in the purefeedback system.

Example 2:Refer to[48],the control scheme proposed in this paperis applied to dealwith the stability ofthe wing rock modelwith ailerons modelled by first-order actuator dynamics under the condition of time-varying full state constraints.Meanwhile,the dynamics equation of the wing rock model is constructed as follows:

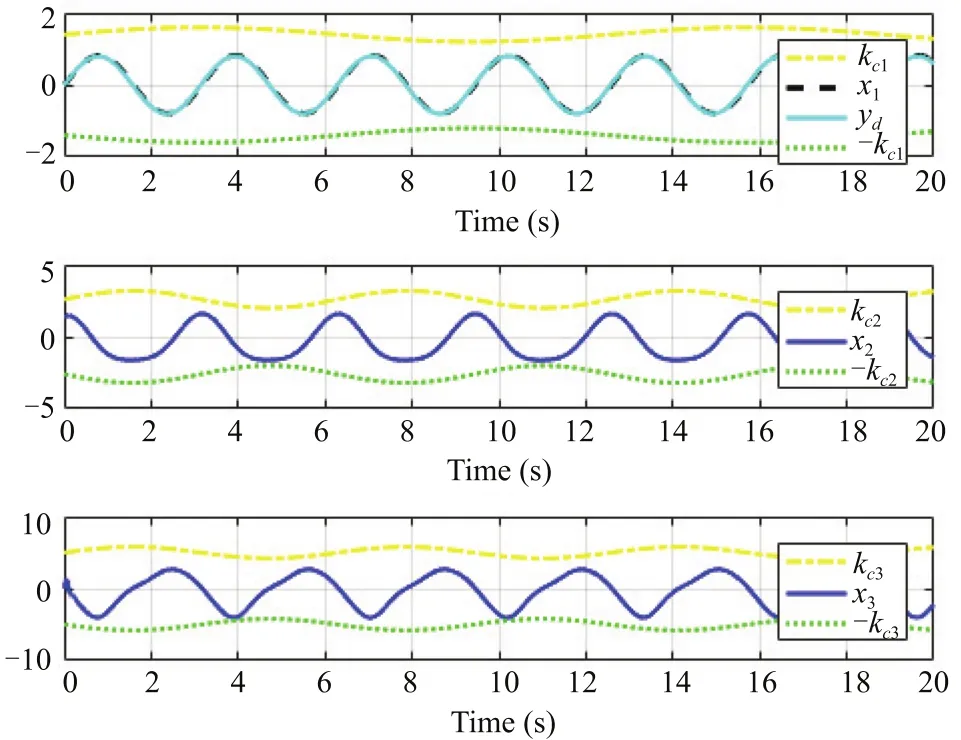
Fig.1.The trajectories of yd,y=x1,x2 and x3.

Fig.2. The trajectories of z1,z2 and z3.

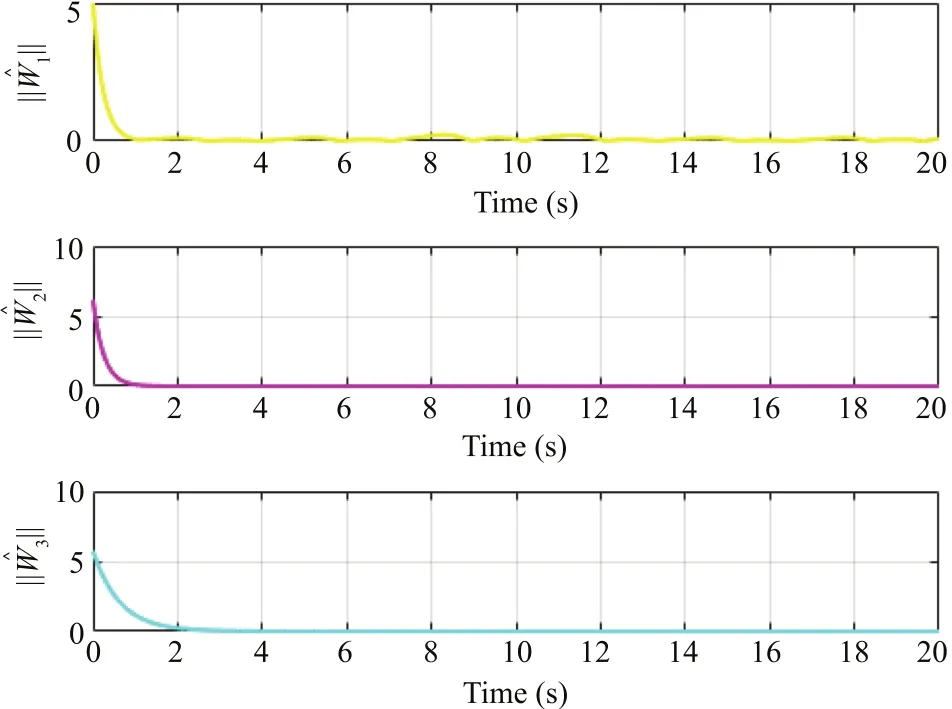
Fig.3. The trajectories of

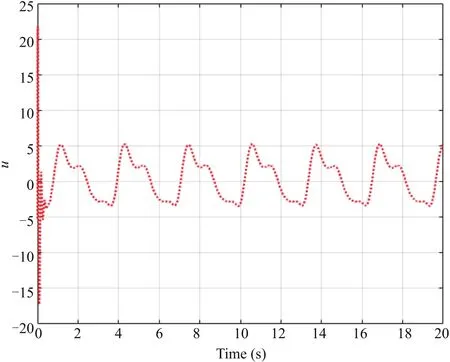
Fig.4. The trajectory of u.

where x1,x2,x3and u are the roll angle,the roll rate,the aileron defl ection angle and the control input,respectively.

The aerodynamic parameters of delta wing for 25°angle of attack are designed as b=1.5,θ0=0,θ1=-0.01859521,θ2=0.015162375,θ3=-0.062445153,θ4=0.00954708,θ5=0.02145291 andω =1/15.

Figs.5-8 are the simulation results of the practicalsystem(67).Fig.5 demonstrates the excellent tracking performance of the system,and shows that time-varying state constraints are never violated.The trajectories of the errors,the adaptive laws and the actual controller are plotted in Figs.6-8.From the above Figures,it is easy to verify the effectiveness of the control scheme proposed in the practical experimental research.

Fig.5. The trajectories of yd,y=x1,x2 and x3.

V.CONCLUSION

Fig.6. The phase portrait of z1,z2 and z3.

Fig.7. The trajectories of

Fig.8.The trajectory of u.

In this paper,we have proposed adaptive NN controlscheme for the nonlinear pure-feedback systems with time-varying full state constraints.The use of BLF prevents time-varying state constraints from being exceeded.The approximation property of NNs is applied to approximate the unknown nonlinear function generated by the controller design process.Though Lyapunov stability analysis and two simulation examples,the proposed controlscheme ensures thatallsignals of the closedloop systems are uniformly ultimately bounded and asymptotic tracking is implemented without violation of constraints.