Fundamental Issues in Networked Control Systems

Magdi S.Mahmoud and Mutaz M.Hamdan

Abstract—This paper provides a survey on modeling and theories of networked control systems(NCS).In the first part,modeling of the different types of imperfections that affect NCS is discussed.These imperfections are quantization errors,packet dropouts,variable sampling/transmission intervals,variable transmission delays,and communication constraints.Then follows in the second part a presentation of several theories that have been applied for controlling networked systems.These theories include:inputdelay system approach,Markovian system approach,switched system approach,stochastic system approach,impulsive system approach,and predictive control approach.In the last part,some advanced issues in NCS including decentralized and distributed NCS,cloud control system,and co-design of NCS are reviewed.

I.INTRODUCTION

A Networked control system(NCS)is a system in which the traditional control loops are closed through a communication network such that signals of the system(control signals and feedback signals)can be exchanged among all components(sensors,controllers,and actuators)through a common network.Fig.1 shows a typical structure of NCS.In comparison with traditional control system,NCS has several advantages including:less wiring,lower cost,and more flexibility and maintainability of the system.As a result,NCS have been used widely in the lastdecades in many fields such as:industrial control,process control,engineering systems,aerospace systems,intelligentsystems,microgrids,and teleoperation,to name a few.However,it turns outthatthe inclusion of networks in dynamical systems introduce new challenges to the overall system due to the appearance of imperfections.These include quantization errors,varying delays,dropouts,etc.The imperfections essentially affect the behavior of the NCS by degrading the performance or causing instability.It is therefore essential to build up an appropriate dynamic representation of the NCS and design effective controllers that achieve stability under these circumstances.

The research of NCS can be classified into two main categories:1) control of network,and 2) control over or through network.Control of network considers the problems of communication network such as communication protocols,routing control,congestion control etc.On the other hand control over or through network focuses on the design and control of systems that are using a network as a transmission media to obtain the desired performance.The second topic“controlover network”,which willbe the subjectof this paper,contains two main aspects:the quality of service(QoS)and the quality of control(QoC).Maintaining both of QoS and QoC is a major objective of research in NCS.Measures of the network like transmission rates and error rates are subjected to QoS,while QoC is concerned with the stability of the system subjected to different conditions.

Fig.1. A typical networked control system.

Severalsurvey papers existin the literature forsummarizing the updated result on NCS.Following a chronological order,[1]reviewed the stability of NCS in 2001.While in 2006[2]provided a generalsurvey on NCS,in which the effectof NCS over the control methodologies of conventional large scale system is reviewed.In 2007,the challenges of control and communication in networked real-time system were presented in[3],and[4]provided an overview on estimation,analysis,and controller synthesis for NCS.Some of the research topics and trends of NCS were presented in 2010[5].A survey on network-induced constraints in NCS was presented in 2013[6].In 2015,[7]has discussed several aspects of NCS such as:quantization,estimation,fault detection and networked predictive control.Also,it presented cloud control issues.Recently,an overview on the theoreticaldevelopmentof NCS was provided in[8]and[9].An overview of the research investigations into the evolving area of NCS was provided in[10].The interaction between control and computing theories was discussed[11].Reference[12]provided a review on event-based controland filtering of NCS.Besides,some results were presented in[13]-[17],and a coverage of analysis,stability and design of NCS can be found in[18].

The objectives of this paper are:First,to provide a review on modeling of the imperfections in NCS.Second,review the theories applied for analyzing and achieving the stability of NCS.Finally,to present some advanced issues in NCS including decentralized and distributed NCS,Cloud NCS and Co-design of NCS.

II.MODELING OF NCS

The components of NCSs are connected via communication systems as shown in Fig.1,and this connection addresses new imperfections and constraints that have to be considered in the modeling of the complete system.As listed in[19],the imperfections and constraints in NCS are classified into five types:

1)quantization errors in the transmitted signals;

2)packet dropouts,because of the unreliable transmissions;

3)variable sampling/transmission intervals;

4)variable transmission delays;and

5)communication constraints,since not all of the signals of sensors and actuators can be transmitted at the same time.

These imperfections are summarized in Fig.2.

Fig.2. Types of imperfections and constraints in NCS.

A.Quantization Errors

Due to the existence of the communication network and its limited transmission capacity,signals have to be quantized before they are transmitted.The controlsignaland plantoutput signal both are quantized before they are sent to the network as shown in Fig.3.A quantizer is a device thatreceives a realvalued signal and converts it to a piecewise constant one with a finite set of values.

In the literature,there are two common types ofquantization which are:logarithmic quantization and uniform quantization.

Fig.3.System configuration of an NCS with quantizers.

1)Logarithmic Quantization:

The logarithmic quantization is considered as static quantization,its performance near the origin is better in comparison with uniform quantization,and it could be either with infinite quantization level or with finite quantization level.The logarithmic quantization with infinite quantization levelis modeled as

where U = {±vi:vi= ρiv0,i = ±1,±2,...}∪{±v0}∪{0},0＜ ρ ＜ 1,v0＞ 0 is the set of the quantization values.The logarithmic quantization with finite quantization level is modeled as

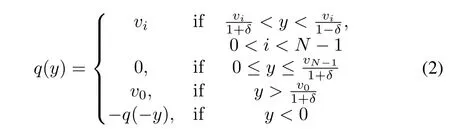
where U={±vi:vi= ρiv0,i= ±1,±2,...,±(N-1)}∪{±v0}∪{0},0＜ ρ ＜ 1,v0＞ 0 is the set of the quantization values.

2)Uniform Quantization:

Uniform quantizer is easier to be operated and it has the following conditions when it is applied with an arbitrarilyshaped quantitative area which satisfies:

where M andΔare the saturation value and the sensitivity,respectively.The upper bound of the quantization error when the quantization is not saturated is represented by the first condition.While,the second condition gives the way oftesting the saturation of the quantization.The rectangular shaped quantitative area is modeled as:

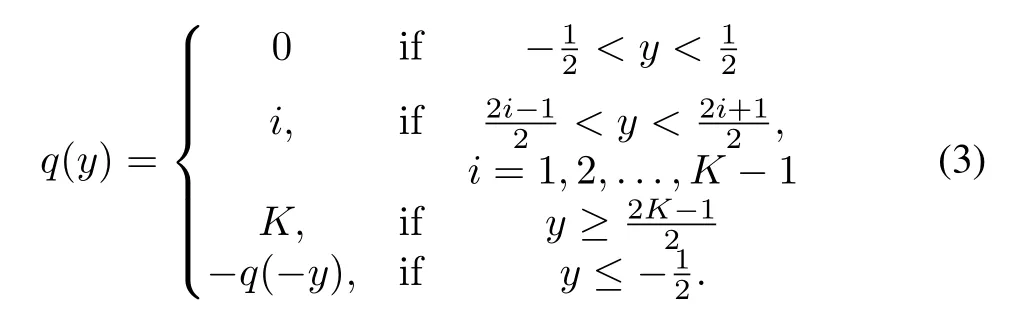
More details about the two types of quantization could be found in[7]and[20].

Remark 1:The logarithmic quantizers are mainly used with linear systems with infinite quantization levels.While,the zoom strategy is a beneficial control policy when uniform quantization is applied,and it has two steps:“zoom-in”and“zoom-out”[7].

Remark 2:The implementation ofzooming-in and zoomingoutwas initially discussed in[21],[22].Itwas used to obtain the sufficient condition for the asymptotic stability for linear and nonlinear systems.

As a result of quantization,information loss will be introduced in the system.Therefore,the modelofNCS hasto take it into account.The quantization error is inversely proportional to the number of bits used for quantization,i.e.,the small number of bits leads to a higher quantization error.Due to this fact,a significant research is directed to determine the minimum number of bits required for achieving the stability of the system,some examples could be found in[21]-[25].

Some researchers focus on controlling the quantization and its effects on the system.Reference[26]proposed a sector bounded approach for dealing with the quantization errors,so its effects on NCS could be investigated using the procedures of robustness analysis.Quantization and stochastic packet dropouts were considered in the study ofthe quadratic stability of NCS and finite quantization was used for implementing the controller[27].The quantizer step size influence on NCS considering packet dropouts and finite-level quantization were studied in[28].In[29]and[30],an adaptable “center”and “zoom”parameters of the quantizers with finite values were considered,the input-to-state stability was obtained by applying a strategy of switching the controller continuously between “zooming-out”and “zooming-in”.The same strategy of “zooming-out”and “zooming-in”was used to obtain parametrized inputto state stability of NCS subjected to packet dropoutand unknown disturbances butwith random lengths of quantization regions based on the packetdropoutprocess[31].Reference[32]has used sector bound and convex combination property of quantizer for determining the sufficient conditions to achieve the desired control of NCS subjected to several categories ofasynchronous sampling and quantization.Quantization with the implementation ofeventtriggering controlwas discussed in many literatures,some examples are:[33]-[37].

Remark 3:There are two phenomena caused by quantization:

1)Saturation,which occurs when the signal is larger than the quantization range and that leads to a higher quantization error causing instability in the closed loop system.

2)Deterioration of the performance around the original point,which occurs near the origin when the signal is not exactly quantized due to the limitation of the accuracy of the quantizers,and this will prevent approaching the asymptotic stability of the closed-loop system.

B.Packet Dropouts

Due to the use of the network for communication,the signals of the systems need to be grouped before transmitting,each group of signals is called “packet”and its size depends on the network used.The transmission of packets could be either single or multiple.In single packet transmission,all data are grouped from sensors or controller and transmitted together.On the other hand,in multiple packet transmission,the data are transmitted in several network packets,causing non simultaneous arriving of data to the controller or actuator.The limited size of the network is notthe only reason of using parallel transmission,but also the distribution of sensors and actuators practically over a large area makes it difficult to lump the data into one network packetleading to use multiple transmission.

Occurrence offailures ormessage collisions on nodes cause packetdropout.To avoid that,mostprotocols use transmission retry mechanisms;However,if the retransmission fails within a limited time,the packets are dropped.Since the communication network is the source ofthe losses,this type ofdropouts is called “network-induced packetdropout”.Moreover,if a new packet sent earlier is available at the node later,it is more practical to discard it and use the recent one,and this type of packet dropouts called “active packet dropout”.For tackling this issue,some techniques like logicalzero-order-hold(ZOH)mechanisms[38]and message rejection[39]were proposed.

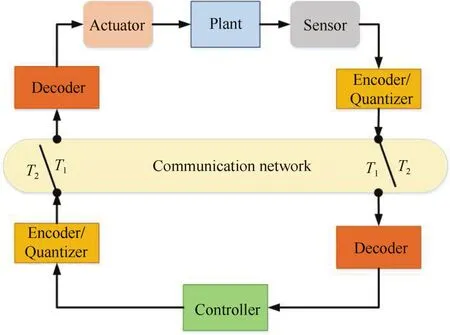
Fig.4.An NCS with quantizers and packetdropoutrepresented by a switch.

One methodology of dealing with packet dropouts is to design the controller to withstand with the upper bound of the dropouts in the system[40],[41],and[42].Another famous approach is to represent the dropoutin the system by a switch[43]-[45].As shown in Fig.4,when the switch is open(T2)the dropout happens,while there is no dropout when it is closed(T1).Then,the relation between the packetdropoutrate and the H∞controller is derived to guarantee the exponential stability of the system.Consider the following discrete-time linear system model of an NCS:

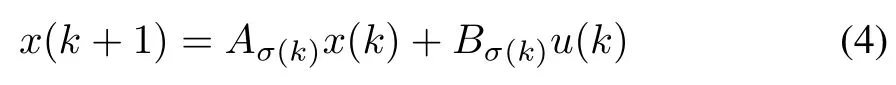
where x(k)is the switched system state,σ(k):R+={0,1,2,...}→Γ={1,2,...,N}is the switching signal which is a piecewise constant function depending on time k and/orstate x(k).The subsystem i is activated whenσ(k)=i,Aiand Biare constant matrices.A hybrid state feedback controller u(k)is used such that

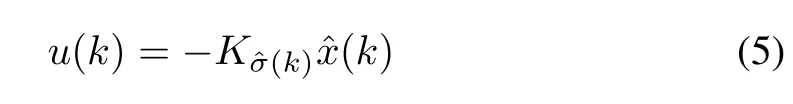
where K is the controller gains to be designed,kis the switched system state,and(k)is the switching signal received by the hybrid controllers over the network.The subsystem i is activated at time P k whenσi(k)=1,and σi(k)=0 otherwise,and thus=1.So,the discrete time switched system is represented by

Now,let s be the transmission indicator function defi ned as

So,the dynamics of the switch system could be described by

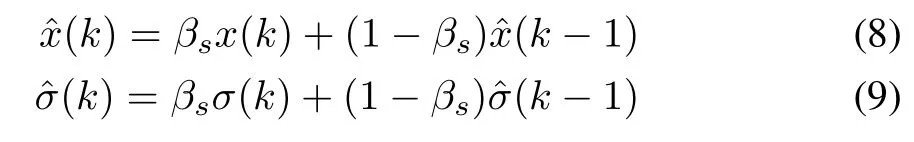
where βsare switch variables such thatβ1=1 and β2=0.By combining(4)-(6),the closed loop networked switched control system with the hybrid state feedback controller is rewritten as

Now,letζ(k)=[x(k)T(k)T]be the augmented state vector,then,the closed-loop networked switched control system with the network packet dropout effect is written as

and here we have two cases,when the switch is positioned at T1,s=1,β1=1,so

When the switch is positioned at T2,s=2,β2=0,so

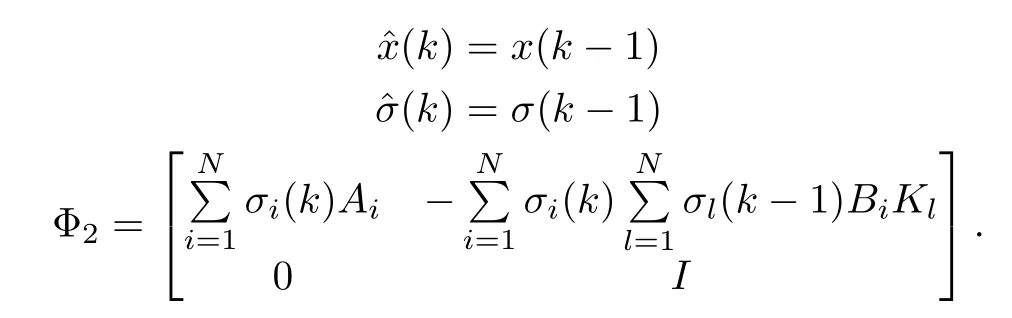
Theorem 1[43]:Forsystem(11),assume thatthe plantstate and the switching signal in a single packetare transmitted ata rate of r.If there exist symmetrical positive definite matrices Pi,Qi,i∈ Υ and scalarsα1,α2＞ 0 such that hold,then system(11)is exponentially stable.

Remark 4:The proof of Theorem II-B could be derived using the following candidate switched Lyapunov-Krasovskii functional:

The other methodology is to consider the packet dropout as a random process,then model it as a Markovian process as in[46]and[47],or as a Bernoulli distribution such as[48]and[49].In[50],the stability analysis and controller synthesis problems were presented for NCS with time-varying delays and affected by nonstationary packet dropouts.The plant is described by the following discrete-time linear time-invariant system

where xp(k)∈Rnis the state vector of the plant and up(k)∈Rmand yp(k)∈Rpare the controlinputand outputvectors of plant,respectively.A,B,and C are real matrices with appropriate dimensions.The measurement received by the controller is affected by a randomly varying communication delay and represented by:

where pkassumes discrete values.So,there are two classes to be considered which are[50]:

Class 1:pkhas the probability mass function where qr-qr-1=constant for r=2,...,n.This covers a wide range of cases[51].

Class 2:pk=X/n,n＞0 and 0≤X≤n is a random variable thatfollows the Binomialdistribution B(q,n),q＞0,that is

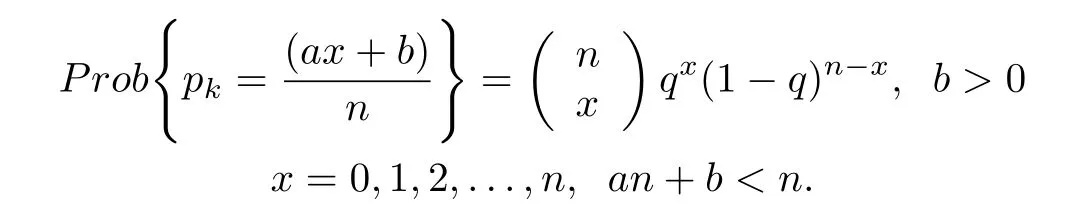
The following observer-based controller is required to be designed in case thatthe fullstate information is not available and the time delay occurs on the actuation side[51]:

Assume that the “actuation delay”and the “measurement delay”are time-varying with bounded conditions as follows:

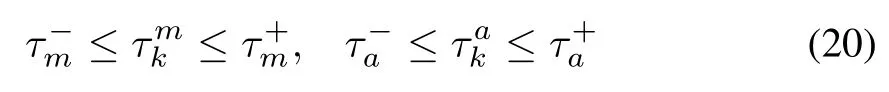
Also,let the estimation error e(k)equal to xp(k)-(k).Then

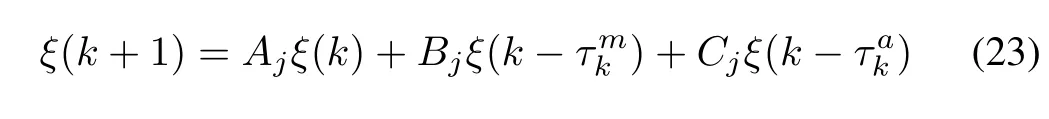
where the matrices{Aj,Bj,CCCj,j=1,...,4}with j is an index identifying one of the following pairs{(δ(k)=1,α(k)=1),(δ(k)=1, α(k)=0),(δ(k)=0, α(k)=0),(δ(k)=0, α(k)=1)}

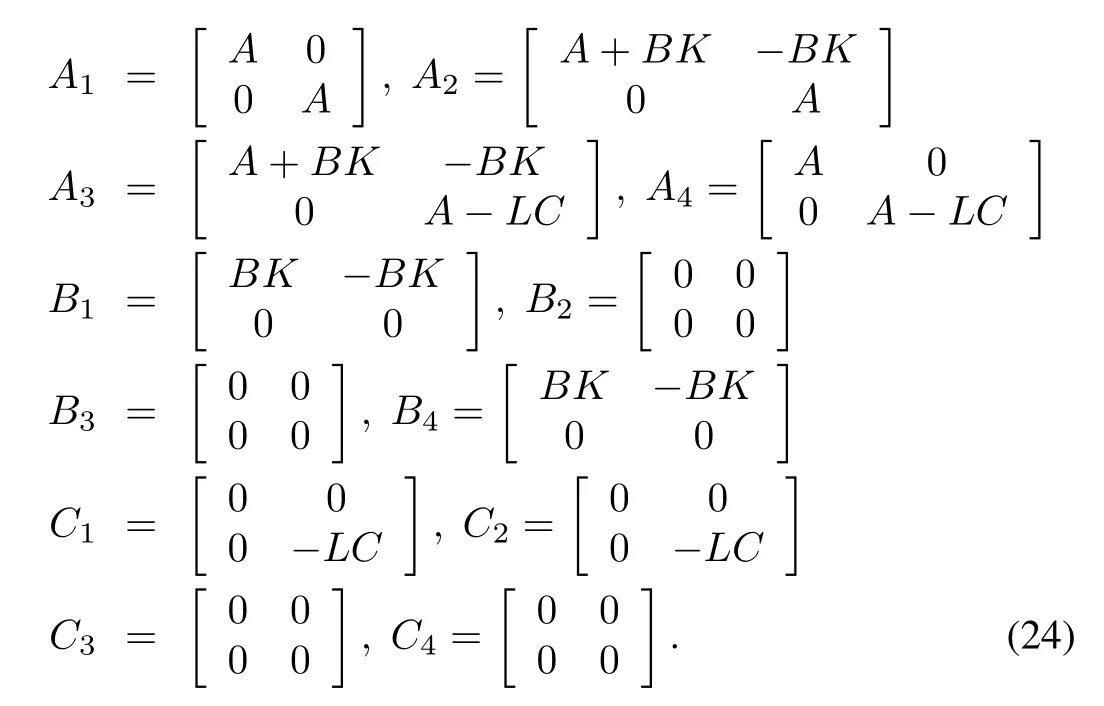
Now,it is desired to design an observer based feedback stabilizing controller in the form of(18)and(19)such thatthe closed loop system(23)is exponentially stable in the meansquare sense.The switched time-delay systems based approach is used to solve this problem[50].

Theorem 2[50]: Let the controller and observer gain matrices K and L be given.The closed-loop system(23)is exponentially stable if there exist matrices 0＜P,0＜= Qj,j = 1,...,4 and matrices Ri,Si,and Mi,i=1,2,such that the following matrix inequality holds

where

C.Variable Sampling/Transmission Intervals

The signals in NCS need to be sampled before the transmission through the network.The sampling periods are usually fixed in conventional systems due to its simplicity in design and analysis,and called:“time-triggered sampling”,“periodic sampling”,and “uniform sampling”.On the other hand,it is varying in the recent NCS since itis waiting in a queue before the transmission process which willbe based on the availability of the network and the protocolused.Itis proved recently that sampling at varying time may have better performance than sampling at fixed intervals[52].

The other method of sampling is event-triggered sampling.It is also called: “Lebesgue sampling”,“level-crossing sampling”,and “magnitude-driven sampling”,etc.,in this case,the sampling and transmission occurs based on triggering of an event such as changing of one of the output signal to a specific value.

There are several approaches for modeling sampled/transmission intervals[52],but the most famous one is the input delay approach due to the using ofthe linearmatrix inequality.By applying this approach,it is easy to determine the maximum upper bound of two consecutive samplings and design the proper controller for the NCS.Letthe system with sampled signal is given by

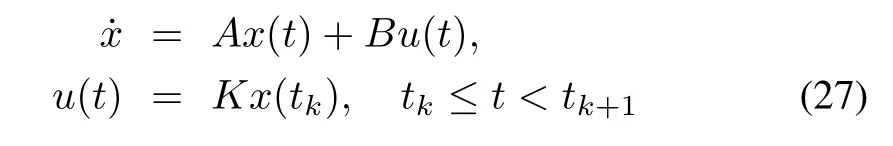
where x(t)∈Rnand u(t)∈ Rmare the state vector of the system and control input vector,respectively.{t1,t2,...,tk,...}is a sequence of sampling such that tk＜ tk+1,limk→∞tk= ∞ and supk{tk+1-tk} ≤ hufor some known hu＞0.

By applying the input delay approach,the above system is rewritten as[53]

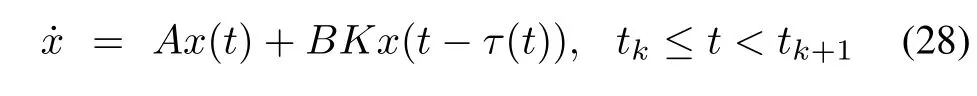
with piecewise time varying delayτ(t):=t-tk,tk≤ t＜tk+1satisfying 0≤τ(t)≤hu∀t≥t0.Using this model,the Lyapunov-Krasovskii functional approach could be used to obtain the stability conditions and formulate the linear matrix inequalities for calculating the admissible upper bound of huand the corresponding controller gain K[53].Other examples of the input delay approach are found in[54]-[59].

D.Variable Transmission Delays

As shown in Fig.5,the NCS has two main kinds of delays:1)Sensor to controller delay,which represents the time between sampling the signal from sensors and receiving it by the controller;2)Controller to actuator delay,which represents the time between generating the control signal and receiving it by the actuator.Some of the sources of these delays are the limited data bandwidth,network traffic,and the used protocols in the network[60].In the early published work,only one of these delays was considered in the design of the controller and it is called one-mode controller.On the other hand,two-mode controller is used to show that both of the aforementioned delays were considered in the model.One of the earlier results on two-mode controller was discussed in[61]-[63],where both of the sensor-to-controller and controller-to-actuator random delays were considered and modeled as Markov chain.

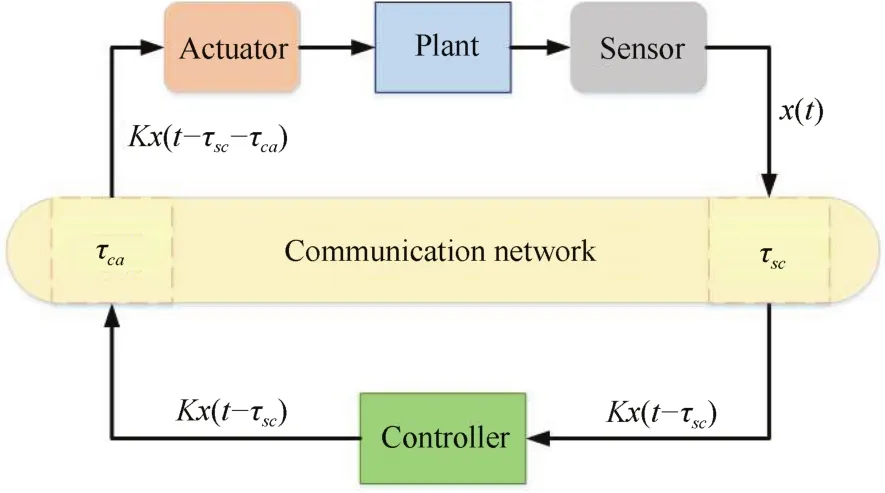
Fig.5.Network induced delay.

The networked induced delay is represented by

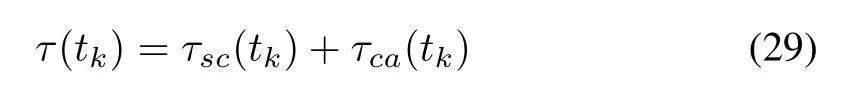
whereτ(tk)is the total networked induced delay at sampling time tk, τscand τcaare the sensor to controller delay and controller to actuator delay,respectively.Fig.6 shows the timing diagram of the signals in NCS.

The overall delay in the NCS is calculated by considering any possible delay in the system such as computationaldelays in the controller,actuator,and sensor nodes[64].So,the complete delay in the system is represented by

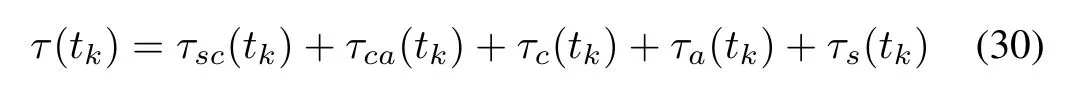
whereτc,τa,and τsare the computational delay in the controller,actuator,and sensor,respectively.Note that u as shown in Fig.5 could be defined as

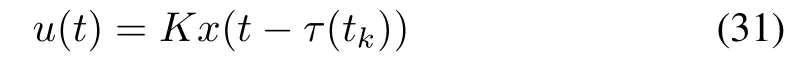
where K represents the feedback control gain matrix.

Remark 5:The induced delay in the NCS(τ)could be extended to consider the dropouts in the system by representing it as a special case of time delay,such that

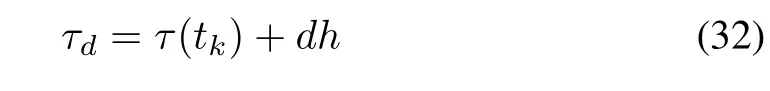
whereτd(tk)is overall delay including the dropouts delay,d is the number of dropouts,and h is the sampling period.

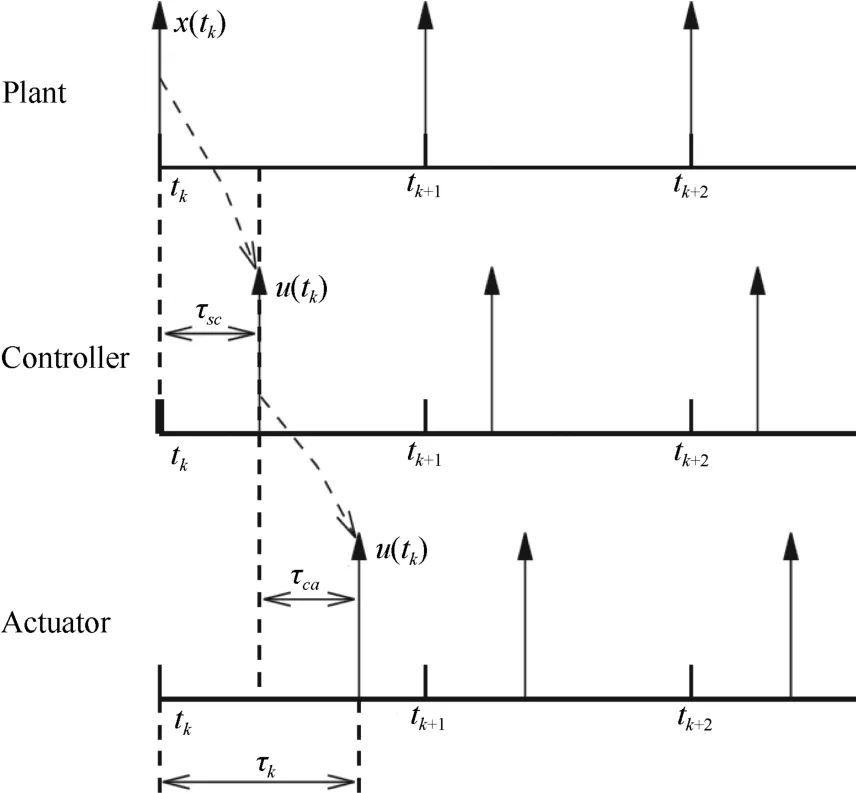
Fig.6.Signals in an NCS with delays.

There are four main models for random delays in NCS which are[65]:

1)Constant Delay Model

The NCS in this model is considered as a deterministic system with a constant time delay normally equal to the maximum delay in the system similar to(29)or(30).It is used when itis difficultto characterize the random delay in the system.Here,a receiver buffer is introduced at the controller(or actuator)node,and its size is equalto the maximum delay(sensor to controller delay or controller to actuator delay)[66]and[67].Thus,the NCS can be treated as a deterministic system,after that,many deterministic control methods can be applied to achieve the stability of the NCS.

2)Mutually Independent Stochastic Delay Model

When the probabilistic dependence is unknown,the constant delay model and the deterministic control strategies could hardly achieve the required performance of the system.The reason is due to the presence of many stochastic factors in networks such as:load in network,competition between nodes,and network congestion,and these factors make the network delay to be stochastic.The delay could be modeled either as mutually independent or probabilistically dependent.

3)Markov Chain Model

This type considers the special dependency relationships among the delays which is the Markov chain.This model has two types:

a)One Markov chain including the sum of delays in the NCS,i.e.,sensor to controller and controller to sensor.

b)Two Markov chains for modeling both sensor to controller delay and controller to actuator delay.

4)Hidden Markov Model

In this model,all of the stochastic factors such as:load in the network,competition of nodes,and network congestion are grouped into a hidden variable and defined as a network state,and this network state governs the distribution of delays.The network state cannot be observed directly butrather it can be estimated through observing network delays,and so,a hidden Markov model is applied to describe the relation between the network state and the network delay.

E.Communication Constraints

In NCS,the communication network is normally shared with sensors and actuators of multiple nodes,and because of the limitation of data transmission,only one or some of these nodes are active ata time and have access to the network.This is the reason behind the communication constraints or some times it is called as “medium access constraint”.As a result,the network requires a protocol for allocating the access of each node to it.This protocolcould be either deterministic or random[68].And so,the model of constraints in NCS could be either deterministic or stochastic.

1)Deterministic Model of Communication Constraints

Previously,the problem was to choose a periodic communication sequence and after that,to design a suitable controller for that[69].But,this method is NP-hard problem as shown in[70].So,the later work was to design the controller first and then to find the suitable communication sequence either off-line[71],[72]or online[73]-[75].Other examples of this type could be found in[76]-[80].

2)Stochastic Model of Communication Constraints

In this modela random media access control(MAC)protocolis used.One example is thata node makes sure thatthere is no other traffic before transmitting its data[68].Examples of this model could be found in[81]-[86].

F.Discussions

As mentioned in the beginning of this section,there are five imperfections thatcould affect NCS.The stability analysis of NCS with two types of imperfections availed the highest level of efforts in the recent years,examples of that are[87]-[92].Table Ishows the references thatdiscussed three or four imperfections.To the best of the authors knowledge,no research has considered all of the five imperfections together.

III.CONTROL OVER NETWORKS

Several methods were developed for stabilizing NCS while considering one or more of the imperfections which have been discussed in the previous section.These methods as listed in Fig.7 include:Input delay system approach,switched system approach,Markovian system approach,impulsive system approach,stochastic system approach,and predictive control approach.A discussion on each of them follows.

TABLE I REFERENCES THAT STUDY MANY IMPERFECTIONS

Fig.7. Theories of control over networks.

A.Input Delay System Approach

The NCS in this approach is modeled as a system with time varying delay including:the delay from sensor to controller,the delay from controller to actuator,and a representation of the dropout as a delay[1],[108].Additionally,the computational delay could be considered in the model as mentioned earlier in(32)[109].Moreover,this approach was developed for considering the signal sampling[55],and were applied for solving the problem of synchronization of complex network[110],[111].

As mentioned in Section II-B,some researchers have considered the disorder of data.A logical ZOH is designed to identify most recently arrived control input signal by making comparison between time stamps of the received signals and then the newest one is used for controlling the process[38].The NCS with the sampler and the logic ZOH is described by the following discrete time system with a delay on the input

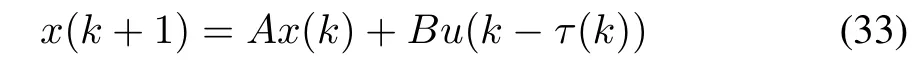
where τ(k)is the inputdelay which is bounded by τmaxsuch that 0≤ τ(k)≤ τmax.By applying a state feedback controller u=K x the overall closed loop system is described by

where K is to be designed and Z+is the set of nonnegative integers.The sufficient condition of stability of the NCS is derived based on a proper Lyapunov function and presented using LMI method as follows[38].

Theorem 3[38]:The NCS described in(34)is asymptotically stable if there exist matrices P∈S+,R∈S+,W1∈ Rn×n,and W2∈ Rn×nsatisfying

where

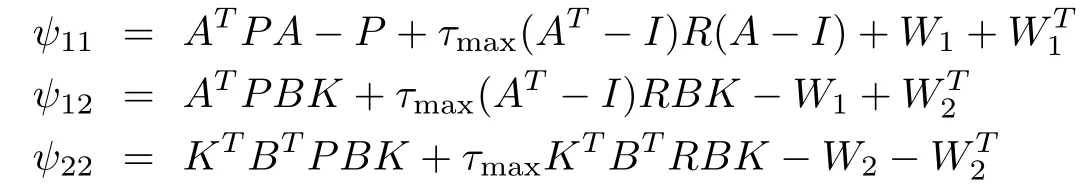
Remark 6:The basis ofproving Theorem 3 is the application of Lyapunov-Krasoviskii stability theory to the following function:

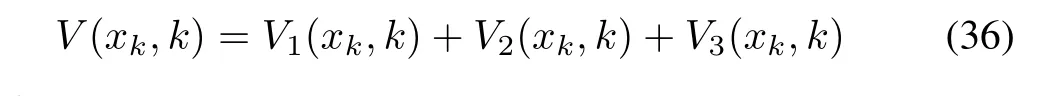
where

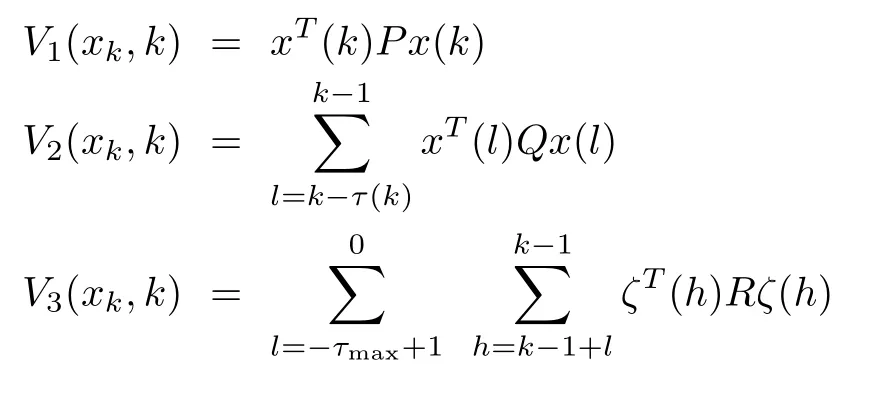
and

Fig.8.An NCS with a master-slave structure.

Another way of analyzing NCS is by using a structure of a Master-Slave system[112]-[114].The control of the system is performed in one PC considered as a Master which communicates through a network with a Slave that includes another PC and the process is as shown in Fig.8.Four delay sources are considered here:communication delay,data sampling,transmitting delay,and the possible packet losses.The Slave is considered to have the following linear form:

where(A,B,C)is controllable and observable andτ1(t)is the total Master-to-Slave delay.

For a given k and for any t∈[t1,k+h1m,t1,k+1+h1m],there exists asuch thatthe proposed observeris represented by

where k′corresponds to the newest output information received by the Master.Now,given a signal g(t)and the global delayτ(t)and packet loss delay h(tk)occurred during the transmission of the packet containing the kthsample at time tk,g(t)can be described by

Now,by using(39),(38)is rewritten as

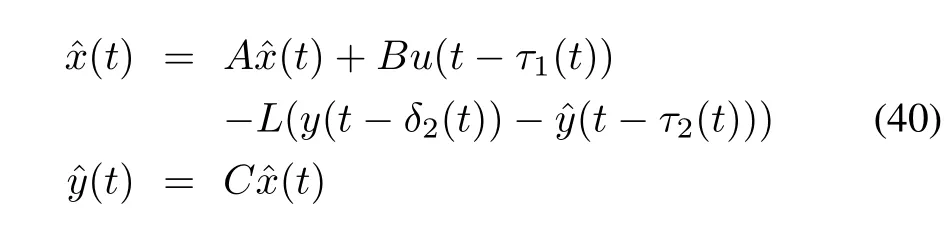
where τ1(t)=h1,k+t-t1,k+d1and τ2(t)=h2,k′+t+d2,The characteristics of the system lead to τ1(t)≤ h1m+T+d1andτ2(t) ≤ h2m+T+d2.Also,the error vector between the estimated state(t)and the real state x(t)is defined as

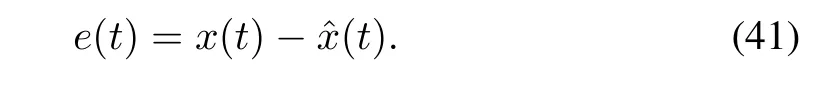
Thus,the error is represented as

Finally,a delay dependentstate feedback controlis designed by the Master based on Lyapunov-Krasovskii functional and the LMIapproach,and a remote observer is used for estimating the states of the Salve.So,a uniform stability is achieved for the system and it is characterized by the following two theorems[113].

Theorem 4 [112]:Suppose that,for some positive scalarsαandε,there exists n×n matrices 0＜ P1,P,S,Y1,Y2,Z1,Z2,Z3,R,Raand a matrix W with appropriate dimensions such that the following LMI conditions are satisfied for j=1,2

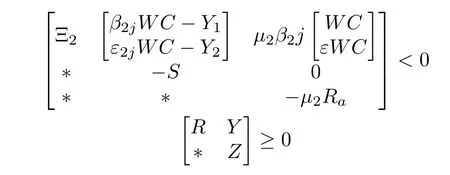
whereβij,i=1,2,j=1,2 are given by

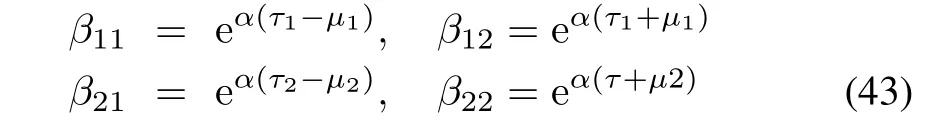
and the matrices Y,Z andΞ2are defined as

Then,the gain

makes the error(42)of observer(40)exponentially converge to the solution e(t)=0,with a decay rateα.

The solution of the LMI problem corresponding to this theorem is written

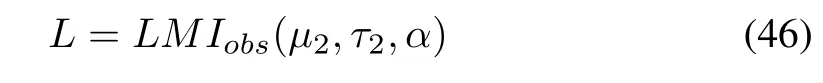
For the control design,consider the controller u=K x,i=1,2,i.e.,the ideal situation e(t)=0,x(t)=(t)and

Theorem 5[112]:Suppose that,for some positive scalars αandε,there exists a positive definite matrix,matrices of size n×n:0＜similar to(44)and an n×m matrix W,such that the following LMI conditions hold

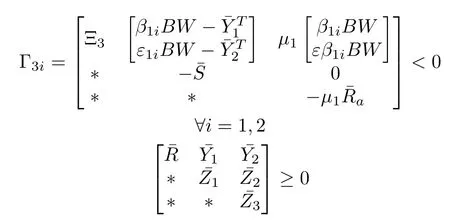
whereβ1ifor i=1,2 are defined by(43)and

Then,the gain

exponentially stabilizes the system(47)with the decay rateα for all delayτ1(t).

The solution of the LMIproblem corresponding to Theorem 5 is written as

Remark 7:The input delay system approach was applied in other researches with other protocols like round-robin(RR)protocol[115]and quadratic protocol(QP)[116]and the results ofboth ofthem were extended and applied on a discrete NCS with actuator constraints[117]and the results were also generated for systems with more than two nodes[118].

B.Markovian System Approach

In this approach,the Markovian model is applied to represent the closed loop NCS.In[46],the Markovian system approach was applied on a vehicle control problem in order to study the effectof packetdropouts on the system which uses a wireless local network,and it has the following description:

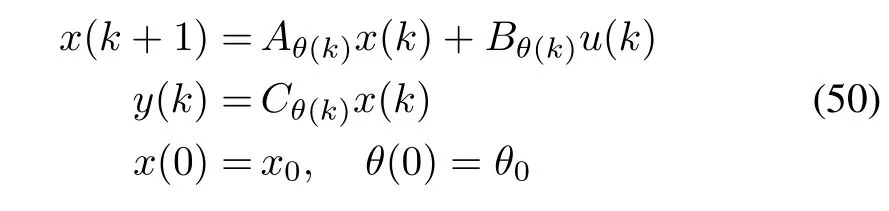
whereθ(k)is the time-varying dependence of the state matrices via the network packet losses parameters,and θis either equal to(0)when the packet from sensor is dropped or equal to(1)when the packet is received.Thus,θ(k)is represented as θ(k) = σ ∈ {0,1}.The state matrices are functions of a discretetime Markov chain with values in a finite set N={1,...,N}.The Markov chain has a transition probability matrix P=[pij]where pij=P r(θ(k+1)=j|θ(k)=i)subject to the restrictions pij≥0 andpij=1 for any i∈N,which means that jumping probability is positive and that the Markov chain has to jump from mode i into some state thathas a probability of one.Using the above model,the stochastic stability is derived for system(50)and represented in an LMI format as follows:

Theorem 6[119]:System(50)is mean square stable(MSS)iff there exists G＞0 such that

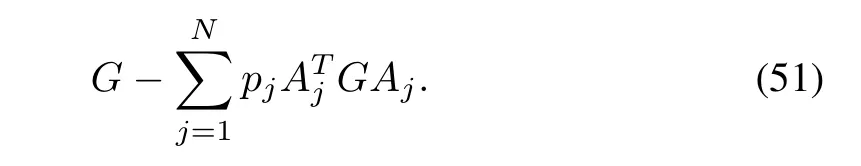
Now,the objective is to design a dynamic output feedback controller that has the following form:

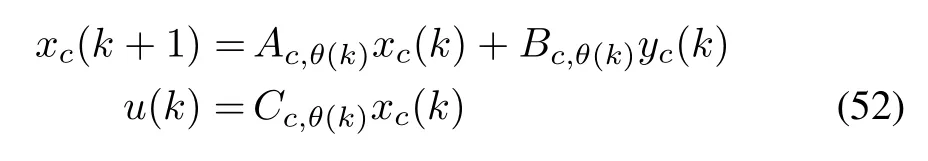
where xc(k)∈Rnis the controller state and the subscript c denotes the controller matrices/states.Again,forθ(k)= σ∈ {0,1},Acσ,Bcσ,and Ccσare used to denote the state space matrices of this two mode controller.The closed loop system is described by:

where the subscript“cl”denotes the closed loop matrices.By applying Theorem 6 and by using Schur complements,system(53)is MSS for the following condition[46]:

where Z=G-1.

In a similar way the model for a NCS with known packet loss was derived as a Markovian jumping system,and then an H∞controller was designed for that system[120].[121]studied the stochastic stability of discrete-time NCS with random delays.Two Markov chains were used to represent the sensor-to-controller and controller-to-actuator delays,and the obtained closed-loop systems are two modes jump linear systems.In[122]the stability of the discrete time NCS contains polytopic uncertainty was considered,where a smart controller is updated with the buffered sensor information at stochastic intervals and the amount of the buffered data received by the controller under the buffer capacity constraint is also random.The exponential stability of generic switched NCS and the exponential mean-square stability of Markovchain driven NCS were assured by establishing the sufficient conditions.

Other examples of literature that had used Markovian system approach are[123]-[128].

Remark 8:A special class of hybrid and stochastic system is called Markovian jump system.This system is applicable in many real systems such as manufacturing systems,power,chemical,economic,communication and control systems.A Markovian jump time-delay system model considering external disturbances of an event triggered NCS was presented in[129],the H∞control problem was solved and sufficient conditions to ensure stability of the closed-loop system were derived.More details aboutMarkovian jump systems could be found in[130].

C.Switched System Approach

The NCS in switched system approach is represented by a discrete-time switched system with a finite number of subsystems.In[131],a discrete-time switched systems with arbitrary switching was formulated for an NCS while considering the effects ofbounded uncertain access delay and packet losses.Then,both of asymptotic stability and L∞persistent disturbance attenuation issues were investigated.The plant is represented by the following continuous linear time-invariant system:

where t∈R+,R+is the positive real numbers,x(t)∈Rnis the state variable,u(t)∈Rmis the control input,and z(t)∈Rpis the controlled output.The disturbance input d(t)is contained in D⊂Rr,and Ac,Bc,Ec,Ccare constant matrices.The control signal is assumed to be time-varying within a sampling period,and the sampling period is divided into a number of sub-intervals in which the controller reads its buffer at a higher frequency than the sampling frequency.The discrete time model of the system is described by

where and C=Cc.Then,the time delay and dropouts effects were added to the model.There are three main scenarios which could occur during each sampling period.

1)If the delayτ=h×T,where T=Ts/N,and h=1,2,...,d1max,then u1[k]=u2[k]= ···=uh[k]=u[k-1],uh+1[k]=uh+2[k]= ···=uN[k]=u[k],and(56)can be written as

2)If a packet-dropout happens with delay less thanτmax,then the actuator will implement the previous control signal,i.e.,u1[k]=u2[k]= ···=uN[k]=u[k-1].Therefor,the state transition equation(56)for this case can be written as

3)The packets are dropped periodically,with period Tmwhich is an integral multiple of the sampling period Ts,i.e.,Tm=mTs.In case of m=Tm/Ts≥2,the first(m1)packets are dropped.Then,for these first(m1)steps,the previous control signal is used.Therefore where the integer N=T s/T,and T is the period of the controller reading its receiving buffers.

During the period t∈[k Tm+(m-1)Ts,(k+1)Tm),the new packet is transmitted successfully with some delay,such thatτ=,where h=0,1,2,...,dmax.And Assuming that d(k T)=d(k T+1)= ···=d(k T+m-1),andmmmthat the controller uses just the time-invariant linear feedback control law,u(t)=K x(t).Then,we may obtain

where

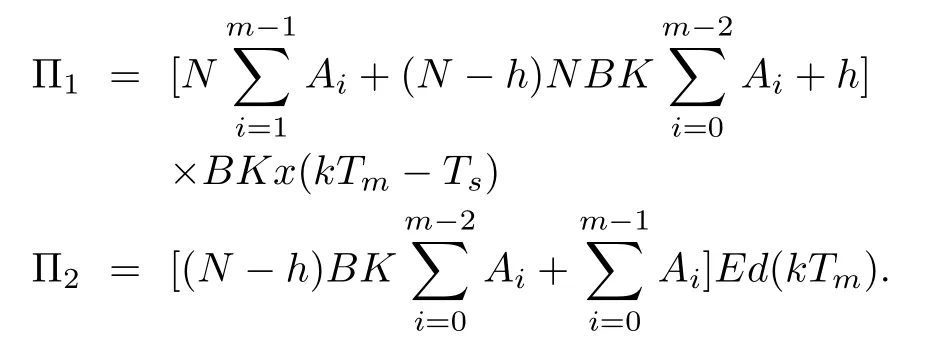
where

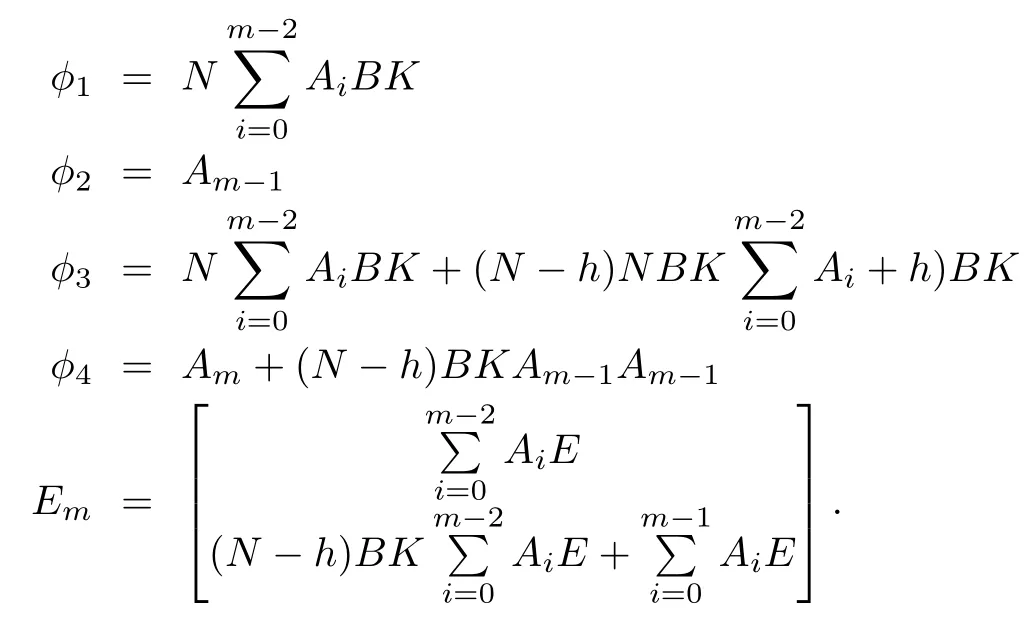
Here m=Tm/Ts≥2 in this case,and h=0,1,...,dmax.

The aforementioned system could be represented in the following format:

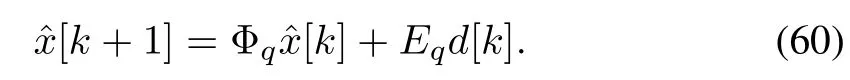
Theorem 7[131]:If the set P(k)⊂ int{X0(µ)}for some k,then the switched system(60)does not admit a positive disturbance invariant set under arbitrary switching in X0(µ),In other wordsµ＜µ∞,where

Pis a positive disturbance invariantfor the switched system(60)with arbitrary switching such that

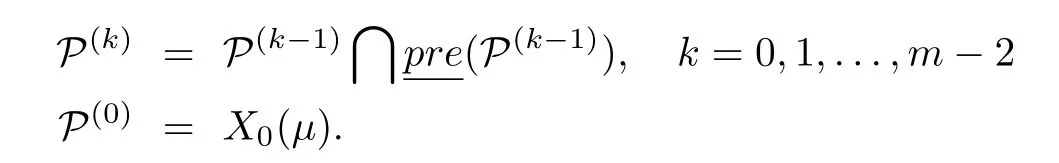
µ∞is the l∞induced norm from d[k]to z[k]and defined asµinf=inf{µ : ‖z[k]‖l∞ ≤ µ ∀d[k],‖d[k]‖l∞ ≤ 1}.

Remark 9:In[131],a systematic proofand detailed stability analysis and l∞persistent disturbance attenuation for the above NCS were developed.Similar works are presented in[132]-[136].

In[137],the continuous time NCS is modeled as an event based discrete-time model while allowing nonuniform sampling and varying delay larger than a sampling period,then the stability is achieved by solving a control problem for a switched polytopic system with an additive norm bounded uncertainty.A discrete-time switched linear uncertain system was used to model an NCS that includes time-varying transmission intervals,time-varying transmission delays,and communication constraints[138].Ateach single transmission,only one known node is allowed to communicate with the network for transmitting its data.Then,a convex over-approximation method in the form of a polytopic system with norm-bounded additive uncertainty was used to determine the stability criteria for this NCS and represent it in an LMI format.The same procedure was followed but with consideration of the quantization of the NCS[107].The asymptotic stability was assured based on quantizer with finite quantization level and the quantizer parameters were suitably adjusted[106].

Remark 10:A switched system approach is implemented for NCS with network-induced delays by defining a switching function.The closed-loop NCS is represented by a time-delay switched system with two switching modes and each mode has a controller with a different gain[139].Stability analysis is carried out based on both the time-delay switched system model and the average dwell time technique.Similarly,the exponential stability is achieved[140].

Other examples of the switched system approach could be found in[141]-[147].

D.Stochastic System Approach

The stochastic system approach is applied when the network-induced delays and/or packet dropouts are random.[148]has discussed the stability of NCS with stochastic input delays,considering the following delayed NCS:

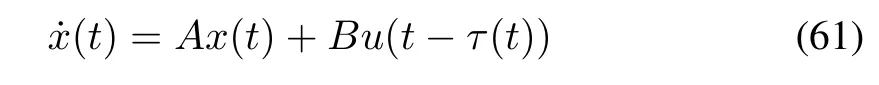
whereτ(t)refers to a piecewise continuous and bounded time delay including the delay from sensor to actuator,the delay from actuator to sensor,and the effectof dropouts.Assuming thatthe probability distribution ofτ(t)is known a prioriwhich takes values in[0,]and(,],and 0≤≤,also,two random events F1,F2are defined forthe stochastic inputdelay τ(t)such that:F1:τ(t)∈[0,]and F2:τ(t)∈(,],and a random variable δ(t)is defined such that δ(t)=1 when F1occurs andδ(t)=0 when F2occurs.Moreover,two functions are definedτ1:R+→[0,]andτ2:R+→such that

Now,by using(62),(61)can be rewritten as

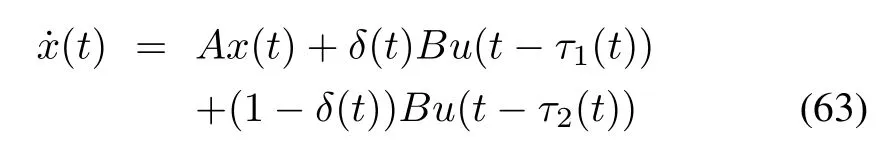
where u(t)=K x(t),K is a constant matrix to be designed,andδ(t)is assumed to have a Bernoullidistribution sequence with P rob{δ(t)=1}=E{δ(t)}= δ0and P rob{δ(t)=0}=1-E{δ(t)}=1- δ0and 0 ≤ δ0≤ 1 is a constant.The closed-loop system of(63)is described by the following formula:

Theorem 8[148]:System(64)is exponentially stable in the mean-square sense if,for given constants,,δ0and matrix K,there exist matrices P＞0,Qi＞0,Ri＞0,Zi＞0(i=1,2),Nj,Mj,Tj,Wj(j=1,2,3,4,5,6),and Sl(l= 1,2,3,4)of appropriate dimensions such that the following LMIs hold:

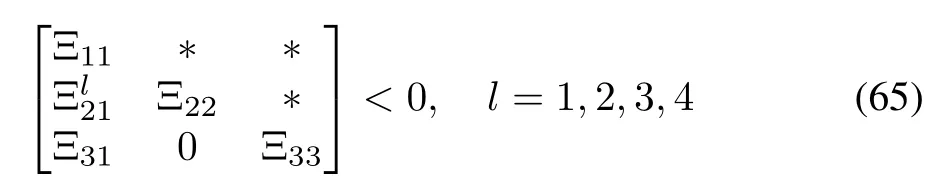
Remark 11:Consider the following candidate function

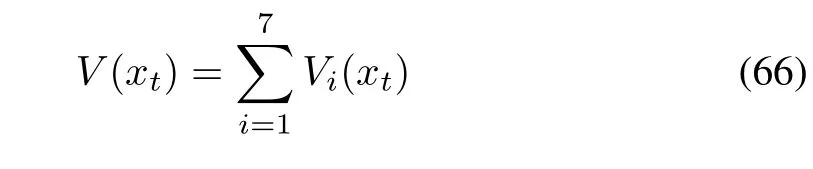
with

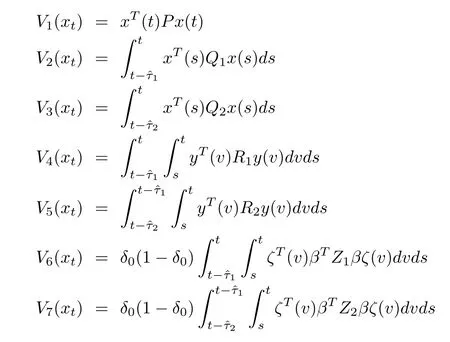
Application of Lyapunov-Krasovskii stability theory to(66)forms the basis of the proof.

A similar result could be found in[149].In[150],random communication delays from sensor to the controller and from controller to actuator through a limited bandwidth communication channel were represented by a linear function of the stochastic variable satisfying Bernoulli random binary distribution,then the exponential stability is achieved by applying an H∞controller.The stability was discussed using a stochastic computational technique in NCS by representing transmission intervals and transmission delays as a sequence of continuous random variables[151].Properties for some inputoutput stability were derived for a general class of nonlinear NCS with exogenous disturbances using stochastic protocols subject to random network-induced delays and packet losses[152].Other examples of using stochastic approach in NCS are found in[153]-[158].

E.Impulsive System Approach

In this approach,the NCS is represented by a hybrid discrete/continuous model or in other words “impulsive system”.An LTI system with uncertainties in the parameters of the process and intervals of sampling was modeled as a linear impulsive system described by the following equations[159]:

where fkand gkare locally Lipschitz functions from RnX R to Rnsuch that fk(0,t)=0,gk(0,t)=0,∀t≥ 0,and the impulse time sequence skforms a strictly increasing sequence in[s0,∞)for some initial time s0≥ 0.Then,a discontinuous Lyapunov function atthe impulse times was used for achieving the exponential stability of system(67).For an NCS with variable sampling time,the objective is to find the maximum allowable time intervalτMATIfor the following general LTI system[159]

where x,u are the state and inputof the process respectively.Atthe sampling time sk,k∈N the state of the system x(sk),is sent to the controller and the control input u=K x(sk)is sent back to the actuator.The resulting closed loop system is modeled as an impulsive system with state ξ(t):=[x′(t)z′(t)]where z(t):=x(sk),t∈[sk,sk+1).So,the impulsive system is describe by:

Theorem 9[160]:System(69)is stable if there exist symmetric positive definite matrices P,R,X1and a matrix N such that

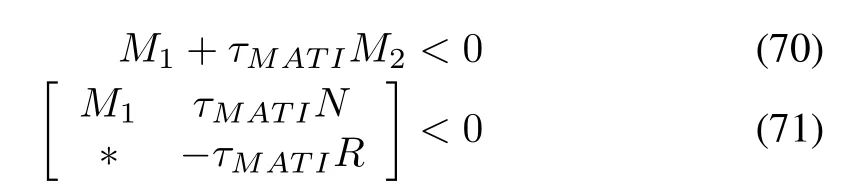
where

Remark 12:Application of Lyapunov-Krasovskii stability theory to the following candidate function:

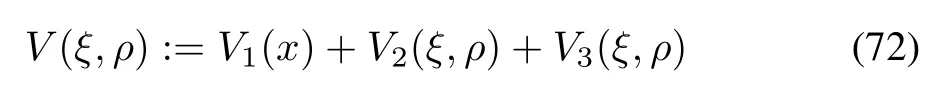
where

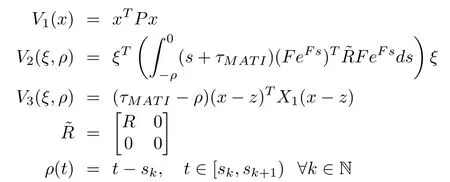
with R,P,and X1as symmetric positive definite matrices.

The Razumikhin technique and Lyapunov functions are applied to achieve exponential stability of an NCS subject to variable bounded delay by applying impulsive control[161].A modelof a threshold-error-dependent augmented impulsive system with an interval time-varying delay is used to design a dissipative control for model-based NCS subject to event triggered communication[162].A delay scheduled impulsive(DSI)controller is presented to achieve a robust stability of NCS subject to integral quadratic constraint and delays[162].Other examples of this approach could be found in[163]-[167].

F.Predictive Control Approach

In this approach,a network predictive controller(NPC)is designed in order to compensate for the effect of time delays and packetdropouts in the network.The NPC scheme consists of two parts as shown in Fig.9:a controlprediction generator and a compensator.A set of future control predictions is generated,packed,and transmitted to the plant side by the controlprediction generator based on the signals received from the sensor.Using the most recent control value from the latest control prediction sequence,the compensator is designed to compensate forthe delays and dropouts thatoccurfrom sensor to controller or from controllerto actuatorchannels to achieve the desired performance.

Fig.9. A network predictive controller scheme.

In[168],an NPC was presented for compensating for the network-induced delay,for the following discrete-time system:

where xk∈Rnis the state vector,ukand yk∈R are the inputand outputvectors,respectively.A,B,and C are system matrices.An output feedback controller is used such that uk= Kkyk.The NPC generates state predictions on the controller side up to time t+τas follows:

where i=2,3,...,dk+τk,...,dk+τandis the state prediction for time k-dk+1 on the basis of the information at time k-dk.And on the controller side,the following control signals are generated

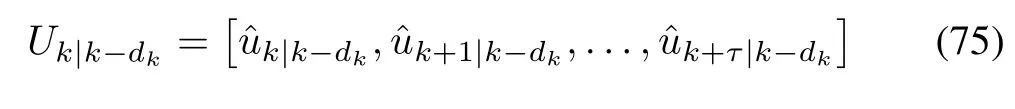
where

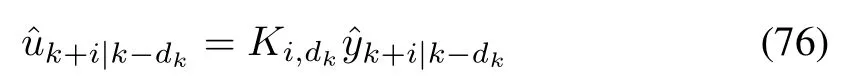
The output feedback control input of the system(73)after applying the NCS strategy is calculated as

where

Then,the Markovian jump systems with discrete and distributed delays could be written as

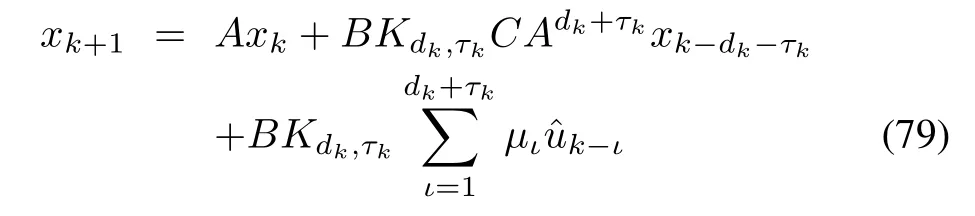
whereι=dk+τk-i+1

Theorem 10[168]:For the NCS in(73)with random delays dkandτkin the feedback and forward channels,where dkand τkare Markov processes,respectively,the closed-loop system in(79)with the predictive controller(78)is stochastically stable if there exist symmetric positive definite matrices Si,j,R,and Q such that the following matrix inequality holds

where for all the i and j

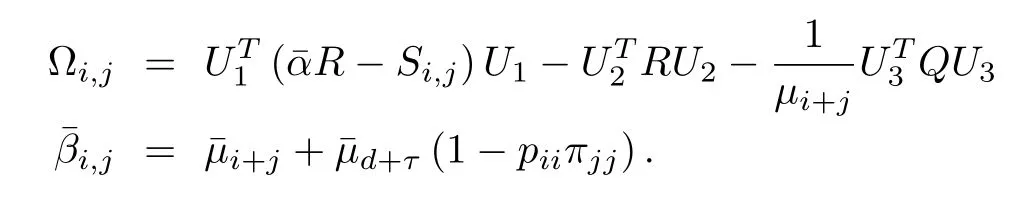
Remark 13:Consider the following candidate function

with

Application of Lyapunov-Krasovskii stability theory to(81)proves Theorem 10.

Other examples of implementing this approach could be found in[169]-[174].

IV.ADVANCED ISSUES IN NCS

A.Decentralized and Distributed NCS

In addition to the centralized configuration of NCS in which a single controller communicates with the system,there are two other configurations which are:decentralized and distributed configurations.Large scale systems are usually modeled as a system of systems or system with subsystems with interconnection among them and several controllers are used for controlling the overallsystem,these controllers either have a communication among them as shown in Fig.10 and it is called decentralized configuration or work separately as shown in Fig.11 and it is called distributed configuration.

Fig.10.Model of a decentralized NCS.

Fig.11.Model of a distributed NCS.

The nodes of the controllers in the decentralized configuration do not share information with nearby nodes.Although the system may have one objective,this causes each controller to work locally.Because of lack of information,a suboptimal control performance may be achieved.Moreover,a deterioration in the system performance and a limitation in the application scope of the decentralized configuration may be occurred in wireless NCS due to the absence of communication and cooperation between decentralized controllers[18].Examples of decentralized NCS are discussed in[175]-[179].

The main features in distributed configuration is that,the exchange of information of each subsystem among components of the system and the plants in order to achieve the objective of the system and which usually contains large number of interacting physicalunits,can be physically distributed and interconnected to others to coordinate their tasks,and this leads to the so-called cooperative control[18].Since sharing oflocal information is allowed among the distributed controllers in this configuration,they have the capability of coordination which leads to modularity,scalability and robustness.Examples of distributed NCS are found in[180]-[186].

B.Cloud Control System

Cloud computing is one of the recent essential tools in industry since it provides customers with a high powerful computation power and itreduces the requirements of the storage.And this opens new windows to the control techniques.Cloud controlsystems have become one ofthe mostpromising directions[187].The structure of cloud control systems is shown in Fig.12.The cloud computing system provides a medium of configurable resources including computation,software,data access,and storage services for practical systems while customers do not need to know the real location and configuration of the service provider during their using of it.

Fig.12.Cloud control systems.

The requirements for computation and communication are increasing in cloud systems due to the increase of the system scale.Generally speaking,in the absence of powerful tools and appropriate system information,most of the complex systems cannot be controlled properly.But,a necessary platform for computability is provided by the development of new technologies,including recentinnovations in software and hardware.Additionally,big data faces a lotof challenges such as:storage,search,capturing,transfer,sharing,visualization,analysis,etc.In the cloud control systems,big data will be transmitted to the centers of cloud computing to be treated fi rstly.Then,control signals,such as scheduling schemes,predictive control sequences and any other useful information will be generated instantly for cloud control systems.So,a powerfultoolfor controlling the complex system,which were not available before,is provided by cloud control systems.

Let us consider the following discrete dynamic system S with unknown process disturbances and measurement noises

where x(k)is the system state,u(k)and y(k)are the system input and output respectively;f(x(k),u(k),w(k))and g(x(k),u(k),v(k))are general models which can be linear or nonlinear.w(k)and v(k)are the unknown process disturbances and the unknown measurement noises respectively.For NCS where there are network induced time delays and data dropouts,ithas been proven thatthe networked predictive method is a very effective method[15]and[187].To estimate the state of the system(82)and then produce the predictive states with finite horizon N1,Kalman filter is adopted as follows:

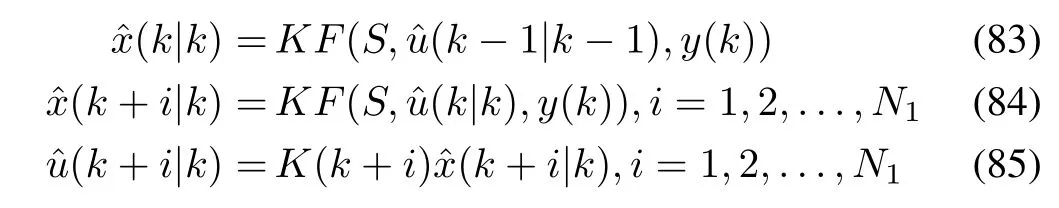
where K F represents the compact form of Kalman filter expression and K(k+i)is time-varying Kalman filter gain.A networked predictive control scheme consisting of a control prediction generator and a network delay compensator is proposed to overcome unknown random network transmission delays[187].The network delay compensator considers the recent control value from the control prediction sequences available on the plant.When there is no time delay in the sensor-to-controllerchanneland the time delay from controller to actuator is kithen,the following predictive control sequences are received on the plant side:

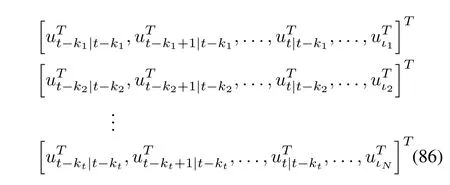
whereιi=t+N-ki|t-k-i and the control valuesfor i=1,2,...,t,are available to be chosen as the control input of the plant at time t,the output of the network delay compensator will be

The controller sends packets to the plant node:

At each time instant k,the actuator selects a preferable control signal to be the actual input of the plant:

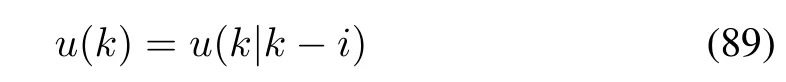
where i=arg mini{u(k|k-i)is available}.

In[188],a cloud predictive control scheme for networked multiagent systems(NMASs)via cloud computing was presented in order to achieve both consensus and stability simultaneously and for compensating actively the communication delays.More information about cloud control could be found in[189],[190].

Remark 14:The principle of cooperative cloud control system is used to describe the system in which two or more cloud controllers are used to achieve the control objectives in form of cooperation.Reasonable allocation for control objectives is however,a difficult dynamic problem[189].

C.Co-Design in NCS

The Co-design of NCS deals with the interaction between control and computing theories.Normally,digital networks are used for connecting sensors,controllers,and actuators in NCS.The concept of centralized control was applied in the previous years in which the sensors,controllers,and actuators are located in an area where the communication is peer to peer.As a result of the short distance,there is no time delay between the NCS parts and also,no packet losses.After that,the concept of decentralized systems was applied since manufactures tend to separate their large plants to subsystems with their own control system with indirect communication.Then,manufactures applied the hybrid systems which contain centralized and decentralized systems.As a result,Internetof things(IOT)became a rising research area in both of academia and industry and it established the future interaction between the computing and communications[11],[187].

Since IOT systems are complex,it is difficult to model them.Practically,the control system faces issues affecting the stability and the overall performance of the system which may lead to instability such as:critical time delay of data,irregularity,time-variance and packet dropout.Traffic congestion could cause losing of data and unreliable nature of the link or protocol malfunctioning[11].On the other hand,the continuous growing of computing systems raises the capabilities to compute,store and process IOT data with high quality and reliable measurements[187].

The implementation of modelestimation,optimization,and controlapproaches into into the progressive data controlcenter was presented in[191]and the implementation of control theory in computing systems was discussed in[192].Two methodologies for remote control systems were proposed in which control system design is provided as a cloud service and hence time and cost were reduced and the design of the plant-wide system became simpler[193].In[194],both communication and control problems were solved simultaneously using co-design approach.[195]proposed a solution for a co-design problem of a mixed event-triggering mechanism(ETM)and state feedback controller for discrete-time linear parameter-varying(LPV)systems in a network environment.A parameter-dependentco-design condition for event-triggered H∞control was given for the problem as a finite setof LMIs.The issue ofperformance limitation ofnetworked systems was discussed by co-designing the controller and communication filter in[196].And itwas shown thatusing the controller and communication filter co-design could deteriorate the performance and revoke the effect of the channel noise.

V.CONCLUSIONS

A survey on modeling and theories of networked control system(NCS)was provided in this paper.In the first part,the modeling of the different kind of imperfections that affect NCS was discussed.These imperfections are:quantization errors,packetdropouts,variable sampling/transmission intervals,variable transmission delays,and communication constraints.Then,several theories which were applied for controlling networked systems were presented.These theories include:input delay system approach,Markovian system approach,switched system approach,stochastic system approach,impulsive system approach,and predictive controlapproach.Finally,some advanced issues in NCS including decentralized and distributed NCS,cloud control system,and co-design of NCS were reviewed.