Observer-based Iterative and Repetitive Learning Control for a Class of Nonlinear Systems

Sheng Zhu,Xuejie Wang,and Hong Liu

Abstract—In this paper,both output-feedback iterative learning control(ILC)and repetitive learning control(RLC)schemes are proposed for trajectory tracking of nonlinear systems with state-dependent time-varying uncertainties.An iterative learning controller,together with a state observer and a fully-saturated learning mechanism,through Lyapunov-like synthesis,is designed to deal with time-varying parametric uncertainties.The estimations for outputs,instead of system outputs themselves,are applied to form the error equation,which helps to establish convergence of the system outputs to the desired ones.This method is then extended to repetitive learning controller design.The boundedness of all the signals in the closed-loop is guaranteed and asymptotic convergence of both the state estimation error and the tracking error is established in both cases of ILC and RLC.Numerical results are presented to verify the effectiveness of the proposed methods.

I.INTRODUCTION

I TERATIVE learning control(ILC),[1]and repetitive control(RC)[2]are two typical learning control strategies developed for systems performing tasks repetitively.ILC aims to achieve complete tracking of the system outputto a desired trajectory over a pre-specified interval,through updating the controlinput cycle by cycle,while RC addresses the problem of the periodic reference tracking and periodic disturbance rejection.The contraction-mapping-based learning control[1]features simplicity,especially reflected in the only use of the outputmeasurements.However,the learning gains are noteasy to be determined because of the difficulty in solving norm inequalities,that may lead to obstacles to the applications of the conventional learning control method.

Early in 1990s,aiming to overcome the mentioned limitation of the contraction-mapping-based method,there have been intense researches in developing Lyapunov-like based designs of iterative learning control[3]-[5]and repetitive control[6],[7].Recently,such Lyapunov-like approach has received further attention[8],[9],[20],[21]-[25].In[8],[9],the learning control problems were formulated for broader classes of uncertain systems with local Lipschitz nonlinearities and time-varying parametric and norm bounded uncertainties.Note that in the mentioned works,the full state information is assumed to be available.However,in many applications,the system state may not be available for the controller design,where it is necessary to design output-based learning controllers in the framework of Lyapunov-like based learning control theory.

For linear systems,Kalman filter[10]and Luenberger observer[11]are two kindsofbasic practicalobservers thatadequately address the linearstate estimation problem.Observers for nonlinear uncertain systems have recently received a great deal of attention,and there have been many designs such as adaptive observers[12],robust observers[13],sliding mode observers[14],neuralobservers[15],fuzzy observers[16],etc.In the published literature,works have been done for outputfeedback-based learning control.In[17],a transformation to give an output feedback canonical form is taken for nonlinear uncertain systems with well-defined relative degree.But the uncertainties in the transformed dynamics should be state independent.In[18],an adaptive learning algorithm is presented for unknown constants,linking two consecutive iterations by making the initial value of the parameter estimation in the next iteration equal to the final value of the one in the current iteration.The results are extended to outputfeedback nonlinear systems.But the nonlinear function of the system is assumed to be concerned with the system output only.

The observers used in learning control are reported in[19]and[20].The former addresses the finite interval learning control problem while the latter addresses the infinite interval learning control problem.The nonlinear functions in[19]are notparametrized and the observer based learning controller is designed in the framework of contraction mapping approach without the requirement of zero relative degree.The observer used in[20]is special and complicated.By virtue of the separation principle,the state estimation observer and the parameter estimation learning law are taken into account respectively.The Lyapunov-like functions are employed and two classes of nonlinearties,the global Lipschitz continuous function of state variables and the the local Lipschitz continuous function of output variables,are all considered.

As is known,repositioning is required at the beginning of each cycle in ILC.Repositioning errors will accumulate with iteration number increasing,which may lead the system to diverge finally.The variables to be learned are assumed to be repetitive.Repetitive controlrequires no repositioning,butthe variables to be estimated need to be periodic.Itis commonly seen that a repetitive signal may not be periodic.RLC has been developed recently[21]-[25],and formally formulated in[24],given as follows:

F1)every operation ends in the same finite time ofduration;

F2)the desired trajectory is given a priori and is closed;

F3)the initial condition of the system at the beginning of each cycle is aligned with the final position of the preceding cycle;

F4)the time-varying variables to be learnt are iteration independent cycle;

F5)the system dynamics are invariant throughout all the cycles.

Unlike the ILC and RC,RLC can handle the finite time interval tracking without the repositioning.In the published literature,however,there are few results on observer-based RLC.

In this paper,through Lyapunov-like synthesis,the ILC problem is addressed for a class of nonlinear systems that only the system outputmeasurements are available.Compared with the existing works,the main contributions of our paper are given as follows.Firstly,the parametric uncertainties discussed in this paper are state-dependent,while the uncertainties treated in the existing results[17]-[19]are assumed to be output-dependent.The state-dependent terms cannot be directly used in the output feedback controller design due to the lack of the state information.Secondly,a robust learning observer is given by simply using Luenberger observer design.Reference[20]pointed out that for learning control systems many conventionalobservers are difficultto apply.We clarify the possibility of designing observer-based learning controller by using a Luenberger observer.The estimation of output,instead of the system output itself,is applied to form the error equation,which helps to establish convergence of the system outputto the desired one.Finally,the method used in output-feedback ILC design is extended to the RLC design.To the bestof our knowledge,the output-feedback RLC problem is still open.In this paper,the fully saturated learning laws are developed for estimating time-varying unknowns.The boundedness of the estimations plays an important role in establishing stability and convergence results of the closedloop system.

The rest of the paper is organized as follows.The problem formulation and preliminaries are given in Section II.The main results of this paper are given in Section IIIand Section IV,providing performance and convergence analysis of the observer based ILC and RLC,respectively.Section V presents simulation results and gives the comparison of the ILC and RLC schemes.The final section draws the conclusion of this work.

II.PROBLEM FORMULATION AND PRELIMINARIES

Consider a class of uncertain nonlinear systems described by

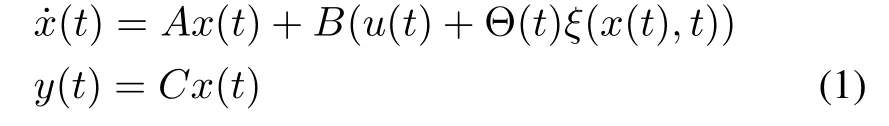
where t is the time.x(t)∈Rn,u(t)∈Rmand y(t)∈Rmrepresent the state vector,the system output and the control input,respectively.A ∈ Rn×n,B ∈ Rn×mand C ∈ Rm×nare known constant matrices.Θ(t) ∈ Rm×n1is the unknown continuous time-varying matrix-valued function and ξ(x(t),t)∈ Rn1is the known vector-valued function.

Remark 1:||Θ(t)||is bounded over[0,T],hence letθmbe the supremum of the||Θ(t)||,butthe value ofθmis unknown.

Assume thatthe system operates repeatedly overa specified interval[0,T].Let us denote by k the repetition index,and system(1)can be rewritten as follows:

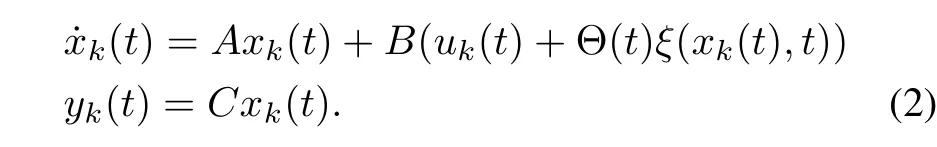
Given a desired trajectory yd(t)=C xd(t)over the interval[0,T],our objective is to design a learning controllaw uk(t),such that the output yk(t)converges to the desired output yd(t),for all t∈[0,T],as k→ ∞.To achieve the perfect tracking,the following assumptions are made.

Assumption 1:For system(2),there exist positive matrices P ∈ Rn×nand Q ∈ Rn×nsatisfying

Assumption 2:Rank(C B)=m.

Assumption 3:The nonlinear functionξ(x(t),t)satisfies global Lipschitz condition,i.e.,∀x1(t),x2(t) ∈ Rn,||ξ(x1(t),t)- ξ(x2(t),t)||≤ γ||x1(t)-x2(t)||,where γ is the unknown Lipschitz constant.

Remark 2:Assumption 1 is the common strictly positive real(SPR)condition.It guarantees the asymptotic stability of the linear part of the system which helps us construct the Lyapunov-like function easily.It also indicates that if(A,B)is completely controllable,(A,C)=(A,BTP)is observable because the matrix P is positive,which makes that the observer can be constructed.Assumption 2 is needed to guarantee the existence of the learning gain in the controller design.The Lipschitz condition in Assumption 3 is commonly seen in observer design and ILC design for nonlinear systems.

For the learning controller design,saturation function sat(·)which is defined in the following ensures the boundedness of the parameters estimation.For scalar f,

Lemma 1:For m×n1-dimensional matrixes F1and F2,if F1=sat(F1),and the saturation limits of sat(F1)and sat(F2)are the same,then

Proof:Itfollows thatfor the matrices F1=(f1ij)m×n1and F2=(f2ij)m×n1

The following property of trace is used as below

where G ∈ Rm×n1,g1∈ Rn1×1and g2∈ Rm×1.

To establish stability and convergence of the repetitive learning control systems in Section IV,the following lemma is given.

Lemma 2:The sequence of nonnegative functions fk(t)defined on[0,T]converges to zero uniformly on[0,T],i.e.,

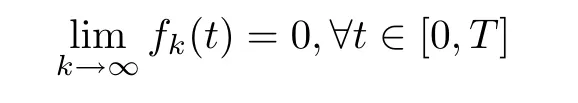
if

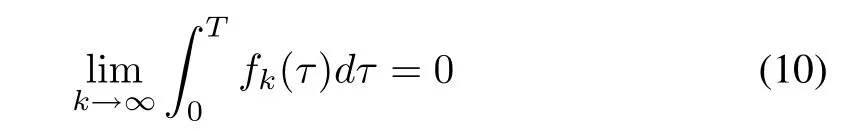
and fk(t)is equicontinuous on[0,T].

The proof of lemma 2 can be found in[19].

III.OBSERVER-BASED ILC

A.State Estimation

By defining the estimation errorδxk(t)=xk(t)-(t),it can be easily derived

where P is defined in Assumption 1,we obtain

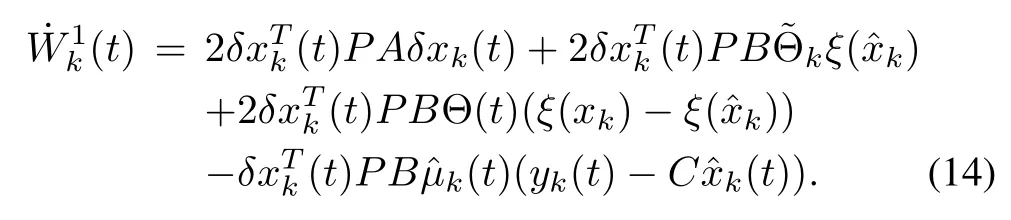
According to Assumptions 1 and 2,we have

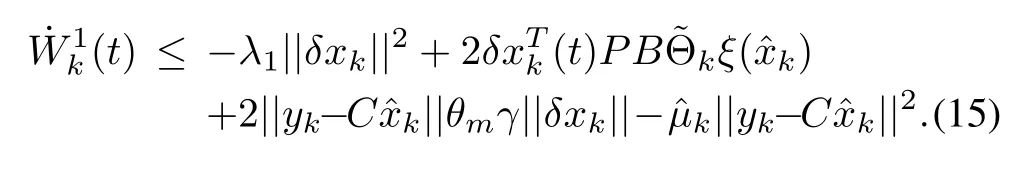
Using the inequality

it can be verified that

B.Full Saturated Iterative Learning Control

Letus define the novelerrorfunction ek(t)=(t)-yd(t),where(t)=C(t).The objective of the learning controller design is to make yk(t)→yd(t),t∈[0,T],as k→∞.Now that the proposed robust learning observer(11)ensures(t)→xk(t),t∈[0,T],as k→ ∞,and the observerbased iterative learning controller will be designed to make(t)→yd(t),t∈[0,T],as k→∞firstly,then the objective can also be achieved.Using(11),the derivative of ek(t)is

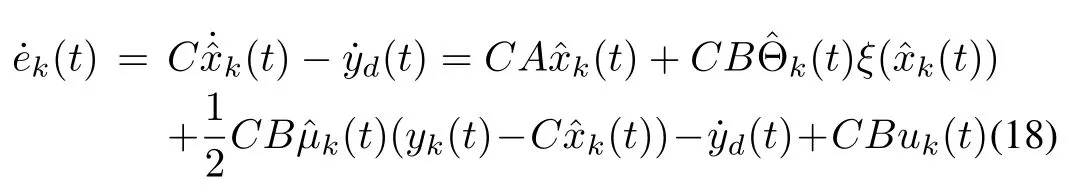
from which we can easily obtain the control law

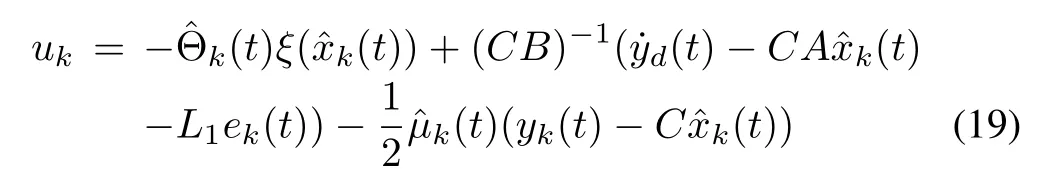
where L1∈Rm×mis a given positive matrix.

Using the following Lypunov function candidate

and considering the control input(19)and the error dynamic(18),we obtain

whereλ2is the minimum eigenvalue of the matrix L1.

It should be noted that the error dynamics(18)is independentof nonlinear uncertainties in system(1),and allvariables in(18)are available for controller design.This is the reason why we use(t)instead of yk(t)in error definition.The controller(19)and the observer(11)work concurrently,where(t)and(t)are updated by the following learning laws

and

where L2=∈Rm×mis a given positive matrix and l3＞0 is a constant.Let us defineΘ(t)={θi,j(t)}m×n1.SinceΘ(t)is bounded,we assume＜θi,j(t)＜,whereandare the saturation limits of the matrix-valued function sat((t)).The saturation limits of the scalar function sat((t))areand,and we assume＜µ＜.

Assumption 4:At the beginning of each cycle,(0)=xk(0)=xd(0).

Remark 3:Assumption 4 is about the initial states resetting condition.This part focuses on the design of observers.An extension of initialstates condition is given in Section IV.See Assumptions 5 and 6.

C.Convergence and Boundedness

Theorem 1:For system(1)satisfying Assumptions 1-4,let controller(19)together with full saturated learning laws(22)and(23),whereis given by observer(11),be applied.Then,

1)allsignals in the closed-loop are bounded on[0,T],and

2)limk→∞||δxk||2=0,limk→∞||ek||2=0,for t∈ [0,T].

Proof:Letus considerthe following Lyapunov-like function

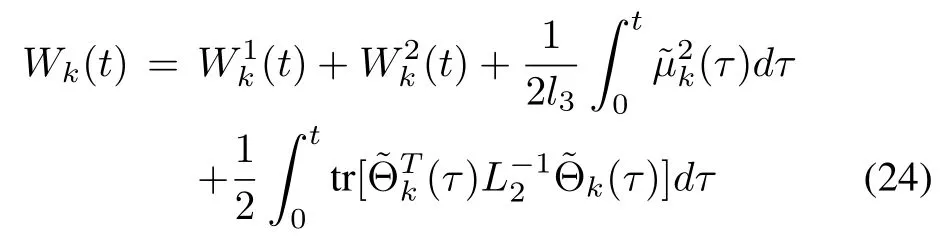
For k=1,2,...,and t∈[0,T],the difference of(24)is

and

Using the equalities

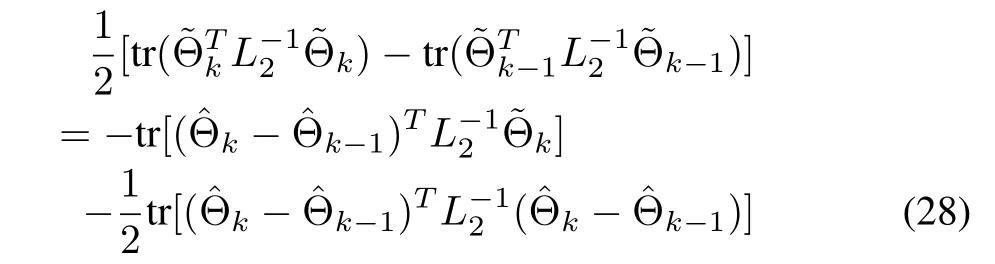
and

and substituting(26),(27)into(25),it can be verified that

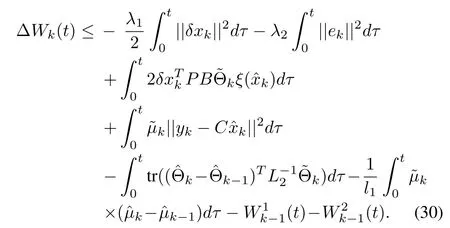
Applying learning laws(22)and(23),inequality(6)and Lemma 1,we obtain

and

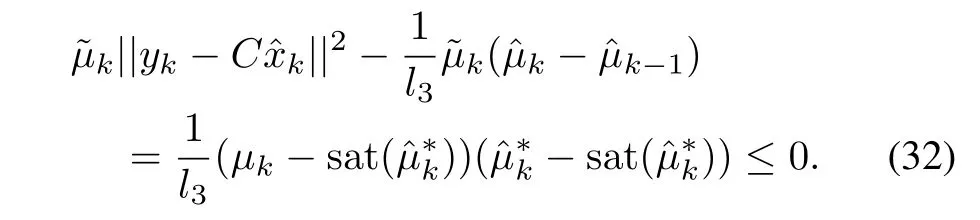
Substituting(31)and(32)into(30)gives rise to

whereλ3is minimum eigenvalue of matrix P.Obviously,Wk(t)is a monotone non-increasing sequence over[0,T],therefore,in order to prove the boundedness of Wk(t),t∈[0,T],we need to prove the boundedness of W0(t)for all t∈[0,T].From(24),when k=0,we have

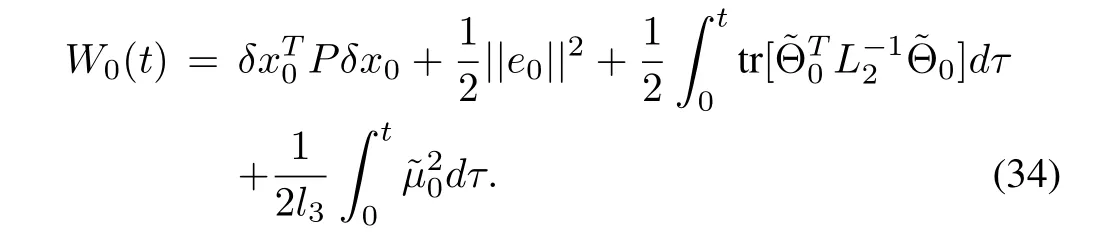
Taking the derivative of W0(t)and using(35),(36)and Lemma 1,we have

From(33),we obtain

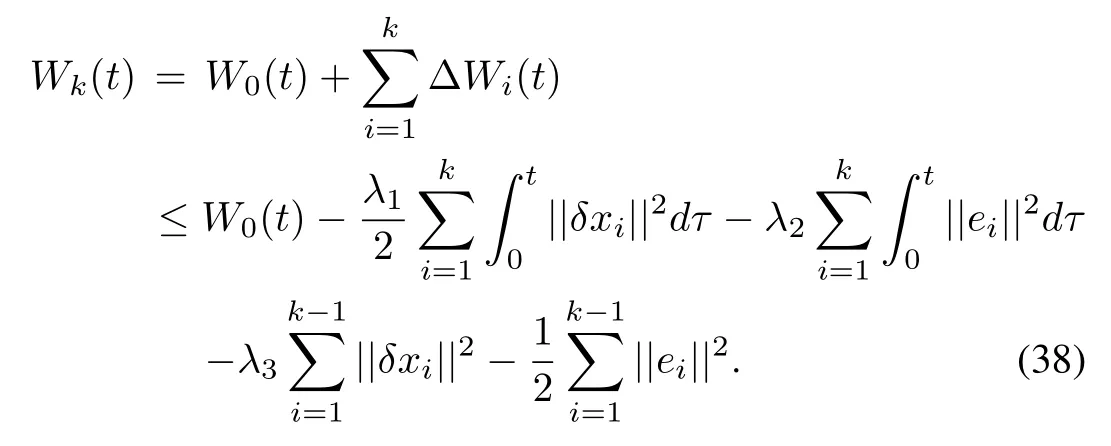
Since Wk(t)is a monotone non-increasing series with an upper bound,its limit exists such that

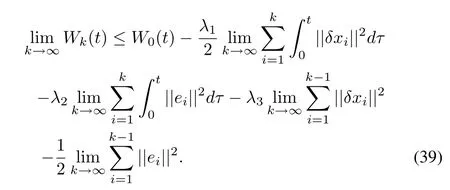
By the positiveness of Wk(t)and the finiteness of W0(t),we have limk→∞||δxk||2=0,limk→∞||ek||2=0,for t ∈[0,T]. ■

IV.OBSERVER-BASED RLC

In this section,we extend the observer-based ILC design into RLC design for uncertain nonlinear systems.The following properties are assumed according to the repetitive learning control formulation.

Assumption 5:The desired trajectory is given to satisfy

and yd(t)is bounded for t∈[0,T].

Assumption 6:At the beginning of each cycle,

Remark 4:Assumptions 5 and 6 satisfy F2)and F3).The initial state estimation condition(42)is required for the observer(11).We do not need Assumption 3 which is a strict condition in practical system.No extra limits of the unknown time-varying functionΘ(t)are needed in RLC,that implies Θ(t)is also repetitive over[0,T]instead of being periodic in repetitive control.

Theorem 2:Considering system(1)with controller(19)and fullsaturated learning laws(22)and(23),where the states are given by the observer(11)over a specified time interval[0,T],if Assumptions 1-3 and Assumptions 5 and 6 are satisfied,

1)all signals in the closed-loop are bounded on[0,T],and

2)limk→∞||δxk||2=0,limk→∞||ek||2=0,for t∈ [0,T].

Proof:Assumptions 5 and 6 imply

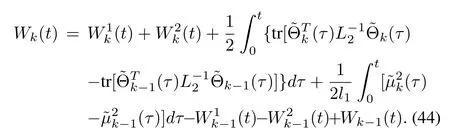
In view of(17)and(21),substituting(28)and(29)into(44),we obtain

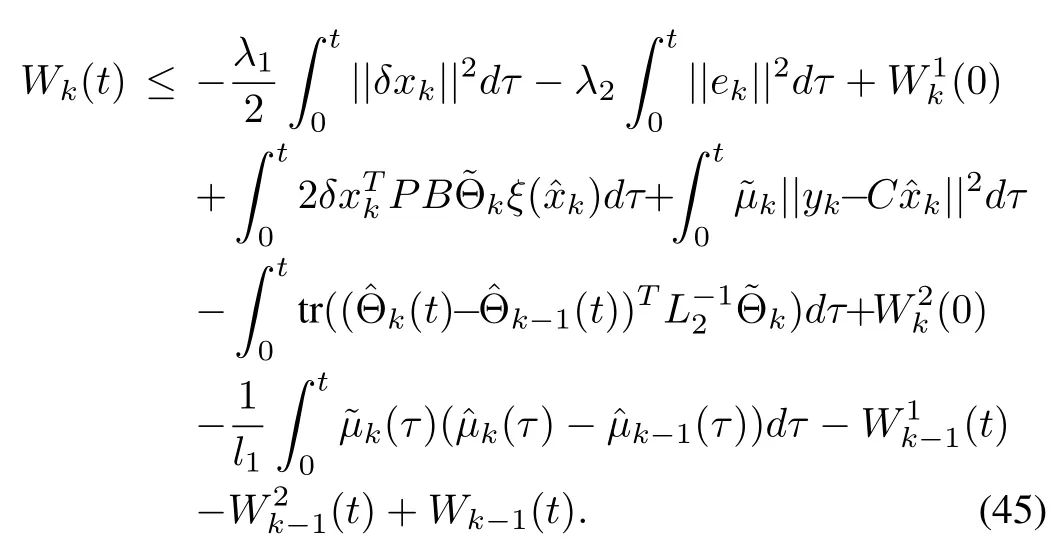
Applying inequalities(31)and(32),we have

In addition,by the definition of Wk(t),we obtain

Therefore,in view of(43),we have

It follows that

It is obvious that the right-hand side of the last inequality is actually the Wk-1(T),which implies

for all t∈[0,T].By setting t=T,we obtain

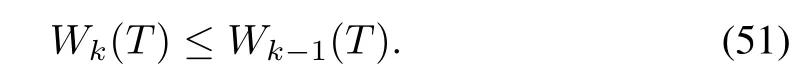
From above,itis clearly seen that Wk(T)is monotonically decreasing.Taking the derivative of W0(t),we can obtain the same result as(37)such that W0(t)is bounded on[0,T].Therefore,Wk(T)is uniformly bounded.Using(50),Wk(t)is uniformly bounded on[0,T].Therefore,||δxk||and||ek||are all uniformly bounded on[0,T].It is seen that the full saturated learning laws(22)and(23)ensure the boundedness of(t)and(t).We can claim that from(19),uk(t)is uniformly bounded on[0,T],and from(18),(t)is uniformly bounded on[0,T],and from(12),δ(t)is uniformly bounded on[0,T].

Setting t=T in(48)results in,

Therefore,

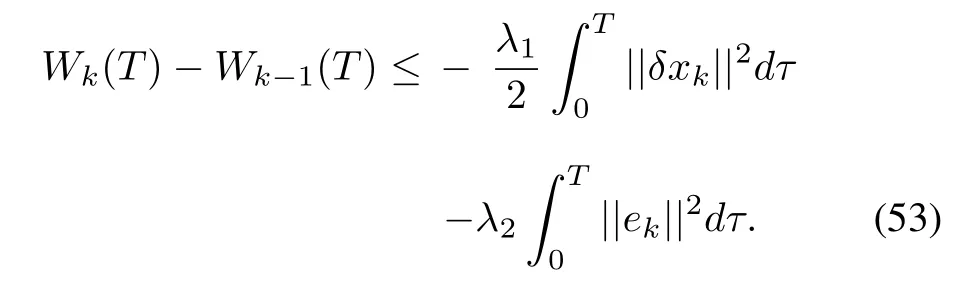
Since Wk(T)≥ 0 is monotonically decreasing and bounded,its limit exists such that

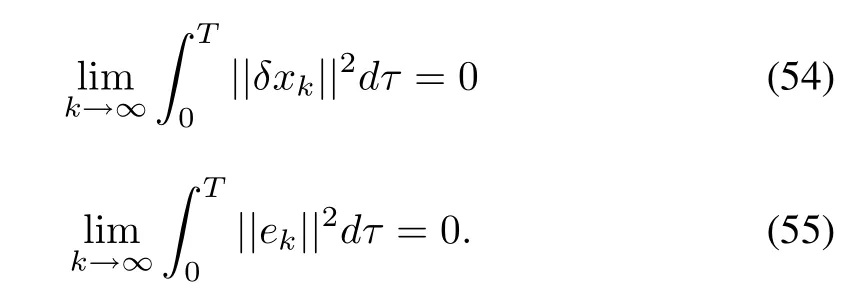
Now,based on the above analysis and using Lemma 1,we can summarize the stability and convergence results as Theorem 2. ■

V.ILLUSTRATIVE EXAMPLES

In this section,two illustrative examples are presented to show the design procedure and the performance of the proposed controllerforthe cases ofILC and RLC,respectively.

Example 1:Consider the following system

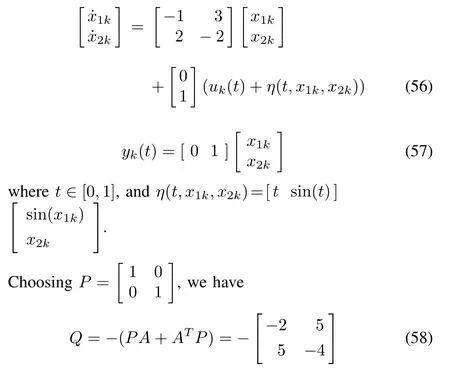
and

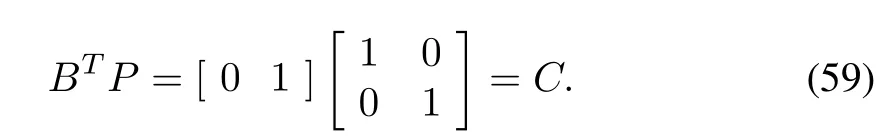
therefore,Assumption 1 is satisfied.

Observer(11),control law(19)and full saturated learning laws(22)and(23)are applied.The desired trajectory is given by yd(t)=12t2(1.1-t),t∈[0,1].We choose L1=0.1,L2=diag{10},and l3=7.Simulation results can be seen in Figs.1-4.In Fig.1,it can be easily seen that the system output yk(t)and the output estimation(t)=C(t)converge to the desired trajectory yd(t)over[0,1].The quantities on vertical axis in Fig.2 and Fig.3 represent=log10(maxt∈[0,1]||δxk||)and Jk=log10(maxt∈[0,1]|ek|),respectively.The learned control quantity uk(t)is shown in Fig.4.

Fig.1. Desired trajectory,output estimation and system output in the case of ILC(k=50).

Fig.2. State estimation errors in the case of ILC.

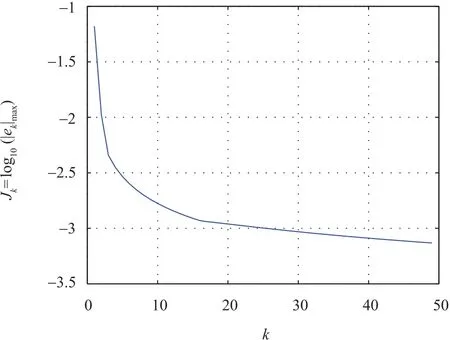
Fig.3. Output tracking errors in the case of ILC.

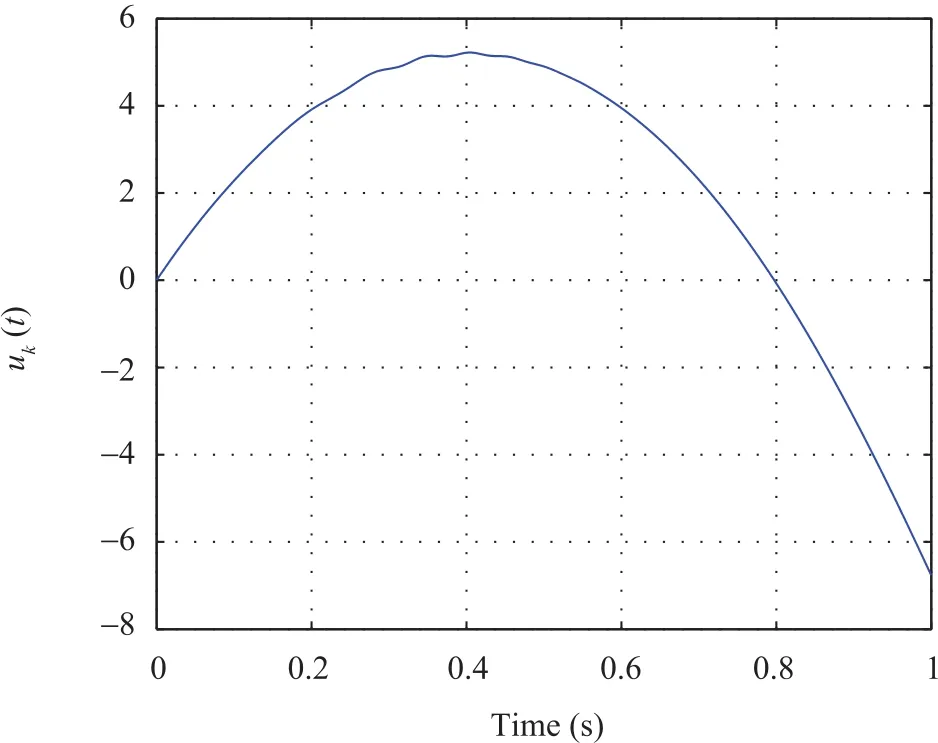
Fig.4.Control input in the case of ILC(k=50).

Example 2:Consider the circuit[20]described by

where R1=1Ω and R2=1Ω are resistors,and M1=0.36H,M2=0.5H are inductors,and the mutual inductors M3=0.5H.x1k=i1and x2k=i2are the loop currents.η(t)=x2ksin3t+0.8 sin2t sin x1krepresents the input perturbation.The desired trajectory is given by yd(t)=12t2(1-t),t∈[0,1].We set L1=0.5,L2=diag{0.8},and l3=1.Simulation results can be seen in Figs.5-8.Fig.5 shows the ultimate tracking of the system output and the output estimation and the desired trajectory.In order to show the difference between the ILC and the RLC,we depict the state x2k(t)of the top 10 iterations in Fig.6.It can be easily seen that the initial value of the k th cycle is equal to the final value of the(k-1)th cycle which satisfies the Assumption 6.

The vertical quantities in Fig.7 represent Jk=log10(maxt∈[0,1]|ek|)which implies perfect tracking can be achieved after 50 iterations.The learned controlquantity uk(t)is shown in Fig.8.

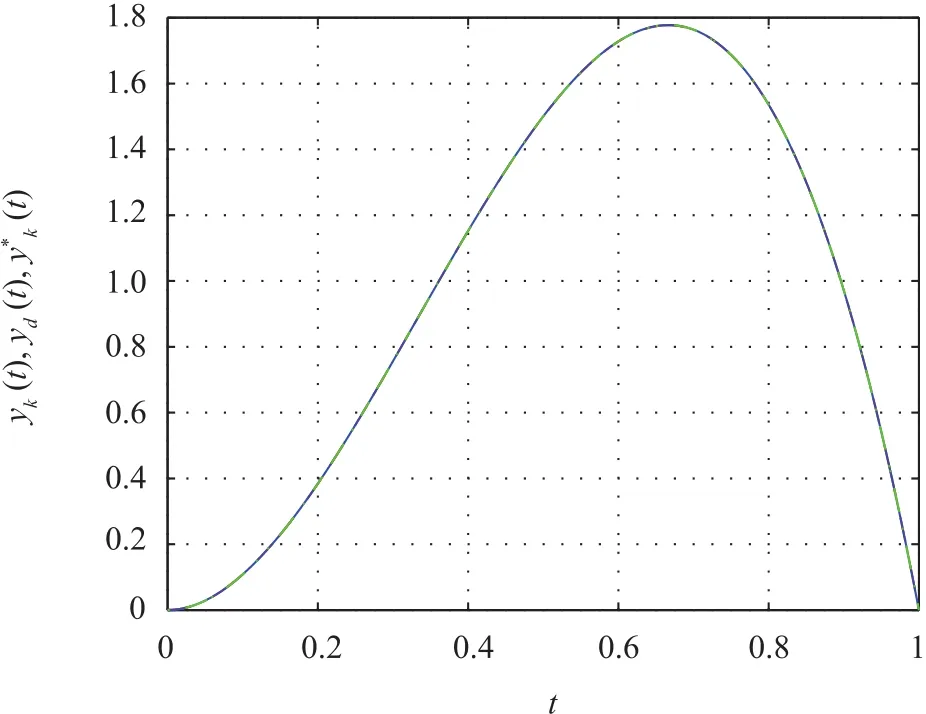
Fig.5.Desired trajectory,output estimation and system output in the case of RLC(k=40).

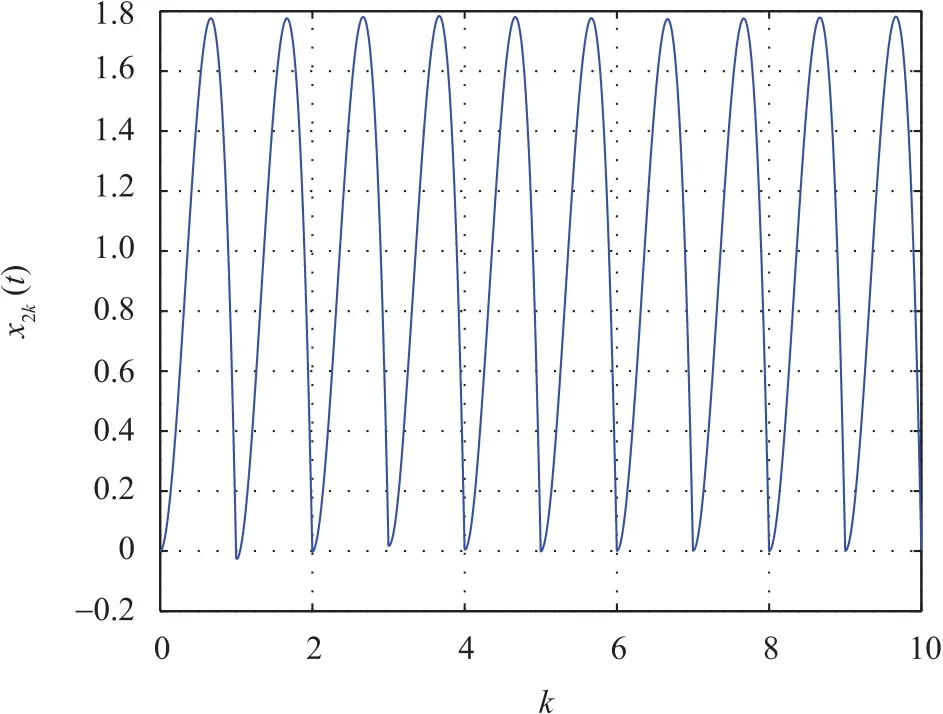
Fig.6. The changes of state x2k(t)in 10 iterations in the case of RLC.

Fig.7. Output tracking errors in the case of RLC.

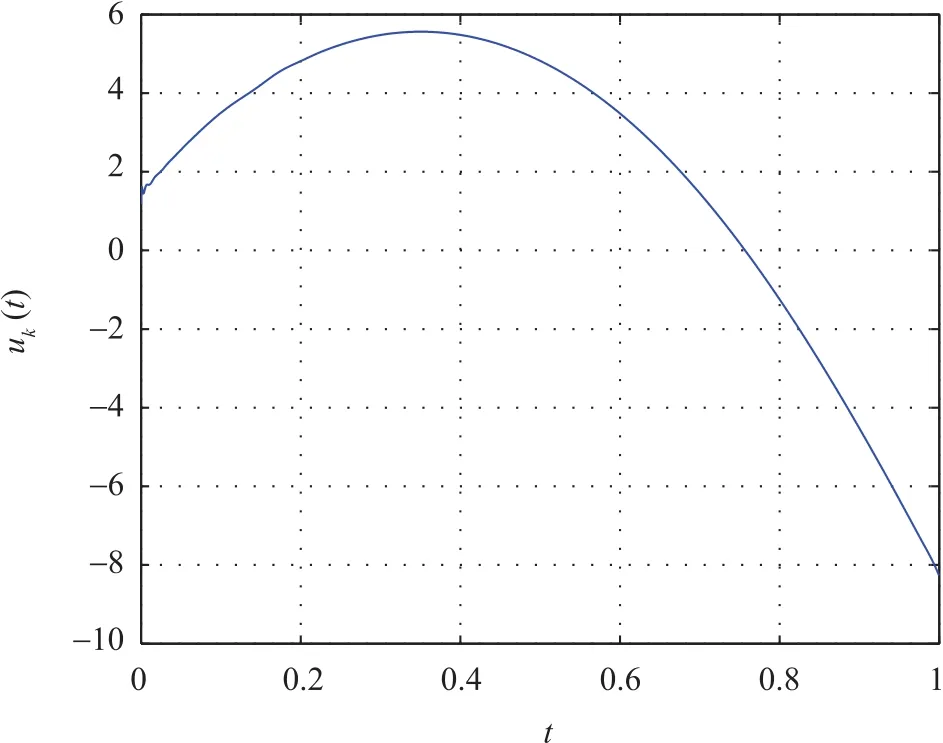
Fig.8.Control input in the case of RLC(k=40).

VI.CONCLUSIONS

In this paper,an observer-based iterative learning controller has been presented for a class of nonlinear systems.The uncertainties treated is parameterized into two parts.One is the unknown time-varying matrix-valued parameters and the other is the Lipschitz continuous function,which is also unknown due to unmeasurable system states.The learning controller designed for trajectory tracking composes of parameter estimation and state estimation which is given by a robustlearning observer.The parameter estimations are constructed by full saturated learning algorithms,by which the boundedness ofthe parameter estimations are guaranteed.Further,the extension to repetitive learning control is provided.The observer-based RLC avoids the initial repositioning and does not require the strict periodicity constraint in repetitive control.The global stability of the learning system and asymptotic convergence ofthe tracking errorare established through theoreticalderivations for both ILC and RLC schemes,respectively.