Modeling of Energy Consumption and EffluentQuality Using Density Peaks-based AdaptiveFuzzy Neural Network

Junfei Qiao and Hongbiao Zhou

Abstract—Modeling of energy consumption (EC) and effluentquality (EQ) are very essential problems that need to be solved forthe multiobjective optimal control in the wastewater treatmentprocess (WWTP). To address this issue, a density peaks-basedadaptive fuzzy neural network (DP-AFNN) is proposed in thisstudy. To obtain suitable fuzzy rules, a DP-based clusteringmethod is applied to fit the cluster centers to process nonlinearity.The parameters of the extracted fuzzy rules are fine-tuned basedon the improved Levenberg-Marquardt algorithm during thetraining process. Furthermore, the analysis of convergence isperformed to guarantee the successful application of the DPAFNN.Finally, the proposed DP-AFNN is utilized to develop themodels of EC and EQ in the WWTP. The experimental resultsshow that the proposed DP-AFNN can achieve fast convergencespeed and high prediction accuracy in comparison with someexisting methods.

I.INTRODUCTION

W ASTEWATER treatment processes (WWTPs) are complexand energy-intensive systems as they require continuousoperation with effluent treatment [1]. In fact, to meetthe effluent discharge standards and reduce the effluent quality(EQ), wastewater treatment plants always run at full loadstatus. It is worth noting that EQ is used to represent the fineswhich are required to be paid due to the discharge of pollutantsin to the receiving water bodies. Under full load status, both ofthe dissolved oxygen concentration(SO)in the aerobic reactorsand the nitrate concentration(SNO)in the anaerobic reactorsare maintained at a high level through aeration and pumping.It is inevitable to remarkably increase the energy consumption(EC). According to the biochemical reaction mechanism of the WWTP,only set-points of SOand SNOare set in a manneraddition, to meet the requirements of energy conservation andemission reduction, it is imperative to realize optimal controlin the WWTP. The design of optimal control strategy mainlyincludes optimization objectives, optimization algorithm, andloop controllers. However, owing to the existing nonlinearcharacteristics and uncertain factors, it is difficult to establishoptimization models of EC and EQ in the WWTP [2].

At present, the mechanism models of EC and EQ aremainly designed by the usage of process variables in theWWTP. Hernndez et al. utilized a non-radial data envelopmentanalysis (DEA) method to calculate the energy indexfor a wastewater treatment plant located in Spain [3]. Yanget al. applied a computational fluid dynamic (CFD) model tooptimize the operating condition by taking into considerationthe flow field and dissolved oxygen concentration [4]. Veraet al. employed a statistical software, called INFOSTAT, toestablish an EC model. However, these mechanism modelshave certain limitations, such as a single decision variable,complex structure, and many parameters [5]. Thus, the predictionaccuracy of these mechanism-based models cannotsatisfy the requirements of multi-objective optimal control inthe WWTP.

The data-driven modeling method has the advantages ofonline detection, short time, and high accuracy. It is widelyemployed to identify the nonlinear dynamic systems. With theability to approach any nonlinear system with arbitrary precision,neural networks have been widely applied to predict thecritical parameters of water quality in WWTPs [6]. Noori et al.utilized a support vector machine to predict the biochemicaloxygen demand (BOD) in order to determine the uncertaintyof the data-driven method [7]. Qiao et al. introduced a softcomputingmethod for BOD, where the T-S fuzzy neuralnetwork with the error backpropagation (EBP) algorithm isutilized to design the prediction model [8]. Kusiak et al.adopted a multilayer perceptron-based data-mining method toestablish the EC and wastewater flow rate models [9]. Hanet al. applied an adaptive regressive kernel function (ARKF)approach to develop an EC model [10]. However, the researchon the modeling of EC and EQ from the perspective of multiobjectiveoptimal control is rare. In addition, since the initialnetwork structure is generated randomly and the parametersare usually adjusted by the EBP algorithm during the learningprocess, the prediction accuracy of the neural network-baseddata-driven models needs to be further improved.

Recent studies have shown that fuzzy neural network(FNN), which combines the learning capability of a neural network with the interpretability of a fuzzy system,has tremendous advantage,and has an extremely extensive application in data-driven modeling[11].To develop the EC and EQ models with the usage of FNN,two issues must be dealt with,including the determination of network structure and the learning ofnetwork parameters.To determine the network size,some flexible clustering methods,such as fuzzy c-means clustering[12],Gustafson-Kessel clustering[13],and K-nearest neighbors clustering[14],are applied to partition the input space.These methods are mainly used for offline modeling.Another class of previously proposed methods,considering that whole training samples might not be available at once,utilizes online modeling[15],[16].However,for these online modeling approaches,the main problem regarding how to produce new rules or prune redundantrules based on some approximate criteria stillremains open.To update the parameters of FNN,the EBP algorithm is adopted frequently.However,as widely reported in the literature,the EBP algorithm has some drawbacks,such as slow convergence,local optimum,and low precision[17].To enhance the learning performance of FNN,various types of learning algorithms have been proposed for the training of FNN,such as hybrid learning algorithm[18],adaptive gradientdescentapproach[19],and evolutionary algorithm[20].However,these algorithms have either poor convergence ability or long training time.

In this paper,a novel fuzzy clustering approach based on the density peaks(DP)is applied to determine the network size.Fuzzy rules with appropriate centers can enhance the generalization performance of FNN.Meanwhile,an adaptive learning algorithm based on the improved Levenberg-Marquardt approach is designed to optimize the parameters of FNN during the learning process.The convergence speed and approximation accuracy of FNN can be enhanced by the combination of density peaks clustering method and adaptive parameter learning algorithm.

The rest of this paper is outlined as follows.The architecture of FNN is introduced in Section II.Section III details the proposed DP-AFNN,including the DP-based clustering method and the improved LM parameter learning algorithm.Subsequently,the convergence of DP-AFNN is discussed in Section IV.In Section V,the proposed DP-AFNN is utilized to develop the nonlinear dynamic models of EC and EQ.Conclusion of the paper is provided in Section VI.

II.FUZZY NEURAL NETWORK

For a multi-input and single-output(MISO)system,the nonlinear continuous time form of the dynamical system can be defined as

where x(t)=[x1(t),x2(t),...,xn(t)]Tand y(t)are the input and output of the nonlinear system attime t,respectively,n is the number of input variables,and f(·)denotes the unknown nonlinear function of the system.

To model the MISO nonlinear system,a four-layer MISO FNN is introduced.The structure of the MISO FNN is shown in Fig.1.The four layers are,respectively,the input layer,the membership function(MF)layer,the rule layer,and the output layer[15].The mathematical description of this FNN is expressed as follows.

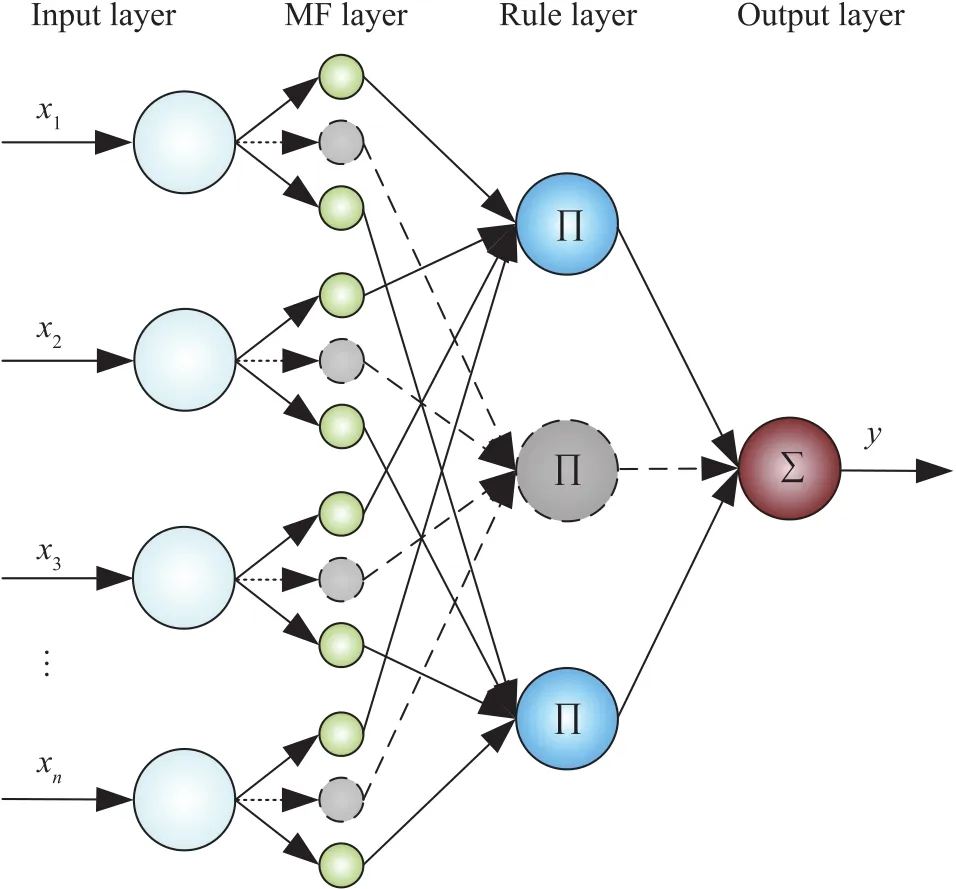
Fig.1.Architecture of the FNN.

The Input Layer:there are n neurons in this layer,and each neuron represents an inputlinguistic variable.The output values of input layer are

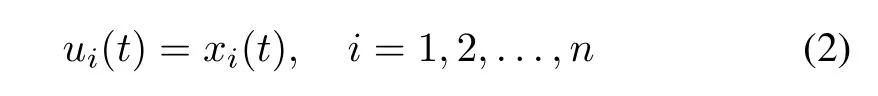
where ui(t)is the outputvalue of the i th neuron attime t,and x(t)=[x1(t),x2(t),...,xn(t)]Tis the inputvector attime t.

The MF Layer:there are n×r neurons in this layer,and each neuron represents a membership function which is in the form of Gaussian function.The outputvalues of MF layer can be expressed as

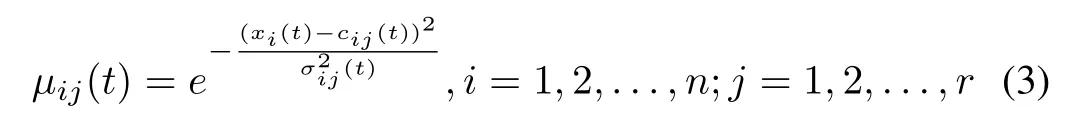
whereµij(t),cij(t),and σij(t)are the output value,center,and width of the j th Gaussian MF of xi(t)at time t,respectively.

The Rule Layer:there are r neurons in this layer,and each neuron represents an antecedent part for fuzzy rules.For the output of MF layer,the product and normalization operators are executed sequentially.The output values of rule layer denote the spatial firing strength of fuzzy rules.For the j th rule neuron,its output value is

and

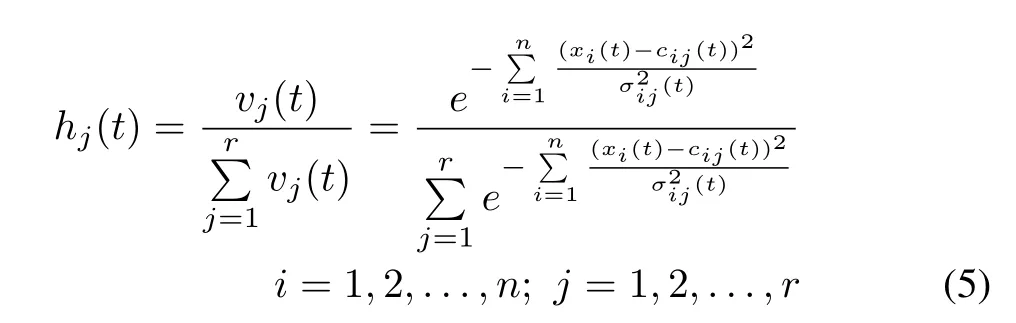
where h(t)=[h1(t),h2(t),...,hr(t)]Tis the normalized output vector of rule layer at time t.

The Output Layer:the output value of this layer is the summation of incoming signals

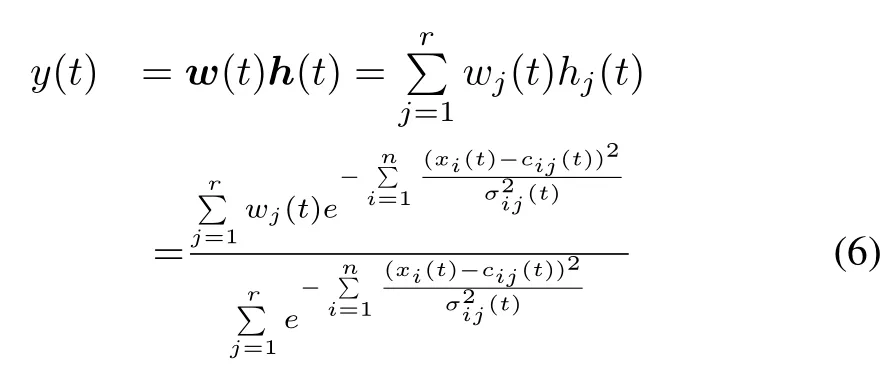
where w(t)=[w1(t),w2(t),...,wr(t)]is the weight vector between the rule neuron and the output neuron at time t.

III.DP-AFNN METHOD

In the following,the principle of the DP-based clustering method is given firstly.Then,the adaptive learning algorithm is described in detail.Finally,the procedure of DP-AFNN modeling is provided.

A.Density Peaks Clustering Method

Recently,a powerful clustering approach based on the density peaks(DP)has been proposed by Rodriguez and Laio in[21].In this study,the DP-based clustering method is applied to partition the input space and to obtain a suitable classification of the training samples.Then,the centers and variances ofthe clusters are utilized as the parameters of FNN.In the DP algorithm,there are two assumptions:1)the cluster centers are surrounded by neighbors which have a lower local density;2)the cluster centers have a relatively large distance from any point which has a higher local density.For the convenience of the searching,two indicators,including the local density ρiand the minimum distance δi,are defined in the DP algorithm.

In the DP algorithm,the local densityρiis given as

where dijis the Euclidean distance between the data point i and j,and dcis a predefined cutoff distance.If x＜0,then χ(x)=1,otherwiseχ(x)=0.Generally,the indicatorρican be obtained through finding data points whose distance to data point i is less than dc.Additionally,dccan also be obtained by setting a percentage parameterα%of all the distance values dijin an ascending order.The recommendedα%is 0.5%∼5%.For example,if the number of training samples is 400 and the percentage parameterα%is setto be 4%,dcis equal to the sixteenth value of all the distances dijin an ascending order.

In the DP algorithm,δiis defined as the minimum distance between the data point i and any other data pointwith higher local density

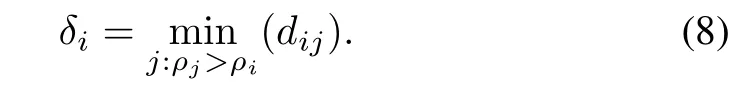
When the point i has the highestlocaldensity,itsδiis setto be the maximum distance between the data point i and other data points.Thus,the data points with large ρiand δivalues are chosen as cluster centers.To avoid setting two thresholds for ρiand δisimultaneously,a scheme to select the cluster center is given by

In the clustering process,data pointwillbe chosen as cluster center if itsγiis larger than the pre-specified threshold.To avoid the setting of threshold,γican be sorted by its value in a descending order and the centers with a fixed number N can be selected.Afterwards,other non-central points are assigned to the cluster which has the highestlocaldensity and the minimum distance to them.

B.Improved LM Algorithm

To avoid trapping into local optimal,the EBP algorithm which has been widely used in FNNs is replaced by an improved LM algorithm in this study.Thereby,the modeling accuracy can be enhanced with the usage of the improved LM parameter optimization algorithm.For the p th sample,the error between the desired output and network output of FNN can be described as

where P is the total number of the samples.

Derived from LM algorithm[22],all the parameters in the FNN,i.e.,centers,widths,and outputweights are adjusted by the following formula

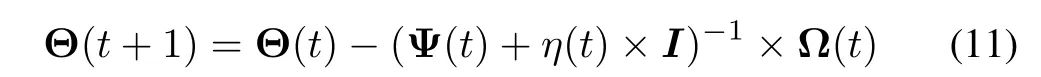
where Θ(t)=[w(t),c(t),σ(t)]is the parameter vector,Ψ(t)is the quasi-Hessian matrix,Ω(t)is the gradientvector,I is the identity matrix which is adopted to circumvent the difficulty of singularity in reversing the matrix.And the learning rate η(t)is given by

where e(t)=[e1(t),e2(t),...,eP(t)]Tis the error vector.The adaptive learning rate can accelerate the learning speed of FNN.Furthermore,theΨ(t)andΩ(t)are the accumulation of submatrices and subvectors for all samples,respectively.

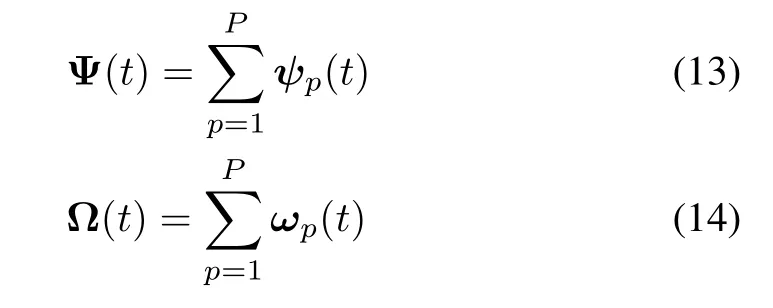
where the submatrixψp(t)and the subvectorωp(t)are defi ned as

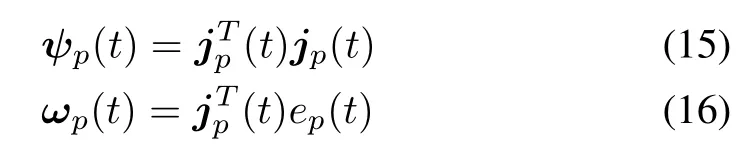
where jp(t)is the row vector of Jacobian matrix

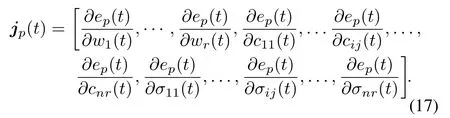
According to the update rule of gradient descent learning approach,the elements of the Jacobian row vector are presented as

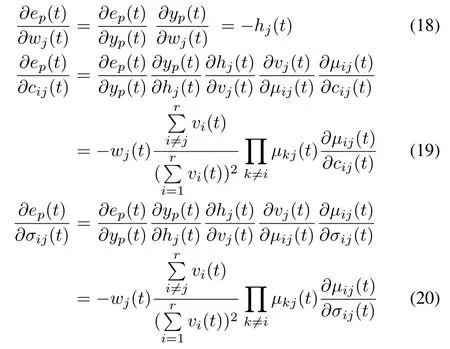
where

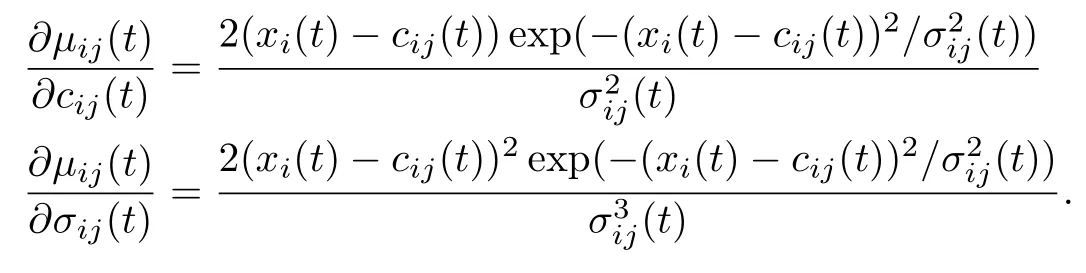
The proposed improved adaptive LMalgorithm is a secondorder parameter estimation algorithm.While computing the submatrixψp(t)and subvectorωp(t)for each pattern p,only(2n+1)×r elements of jp(t)are needed.It should be noted that there is no need for storing and multiplying Jacobian matrix in the computation of quasi-Hessian matrixΨ(t)and gradient vectorΩ(t).Thus,the memory cost and computational complexity can be significantly reduced.Furthermore,the improved LM algorithm with the adaptive learning rate can not only accelerate the learning speed,but also enhance the generalization capability.

C.Procedure of DP-AFNN Modeling

To reveal the proposed modeling method clearly,the design steps ofthe models of EC and EQ with the usage of DP-AFNN are summarized as follows.

Step 1:Generate enough process data about EC and EQ using BSM1 and execute data normalization operation.

Step 2:Calculate the local densityρfor each data point according to the predefined percentage parameterα%.

Step 3:Calculate the minimum distanceδfor each data point.

Step 4:Compute the cluster center selection parameterγ for each data point,sortall data points by theirγvalues in a descending order,and select the first N data points as cluster centers.

Step 5:Create two initial four-layer FNN.The number of neurons in the inputlayer is the same as the number of input variables.The initial centers of fuzzy rules are the centers of clusters.The initial widths of all fuzzy rules are set to be the variances of clusters.The initial output weights of DPAFNN are set to be the outputs of training samples which are selected as the centers of fuzzy rules.The maximum number of iterations is set to be T.

Step 6:Calculate the network output y(t)for each training sample.

Step 7:Make the error e(t),submatrixψ(t),and subvector ω(t)for each training sample.

Step 8:Make the accumulation of submatricesΨ(t)and subvectorsΩ(t)for all the training samples.

Step 9:Update the learning rateη(t)and the parameter vectorΘ(t).

Step 10:Stop and evaluate the test samples if the stopping criteria is satisfied.Otherwise,go to Step 6.

IV.CONVERGENCE ANALYSIS

The convergence of the proposed DP-AFNN is of great importance for modeling EC and EQ.In this section,our analysis suggests that the convergence of DP-AFNN can be guaranteed.

We choose the Lyapunov function as follows

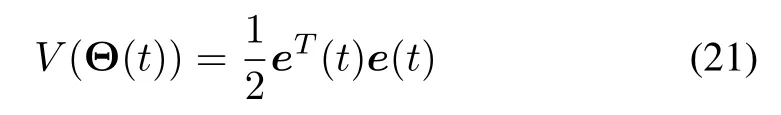
where e(t)=[e1(t),e2(t),...,ep(t)]Tand V(Θ(t))＞ 0.The difference between the Lyapunov function in the nexttime step and in the present time step is determined as follows

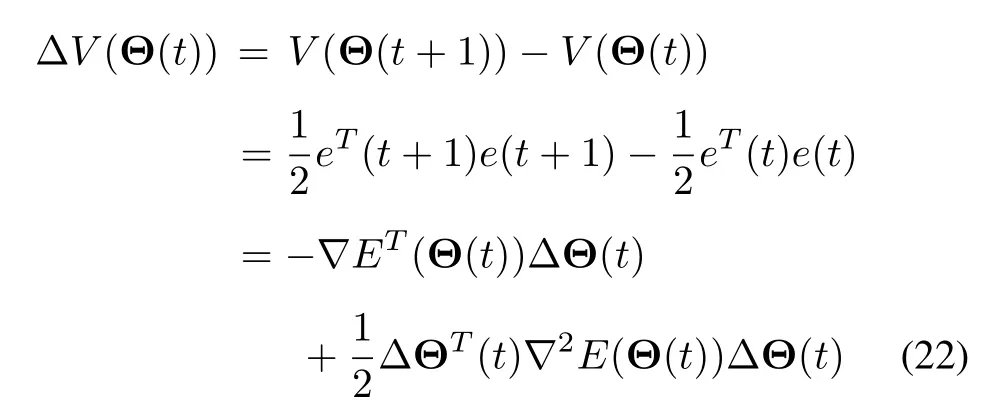
where∇E(Θ(t))and∇2E(Θ(t))are the gradientvector and the matrix of second derivative(or Hessian matrix)of the cost function,respectively.In[22]and[23],when the parameters of DP-AFNN are updated by(11),if

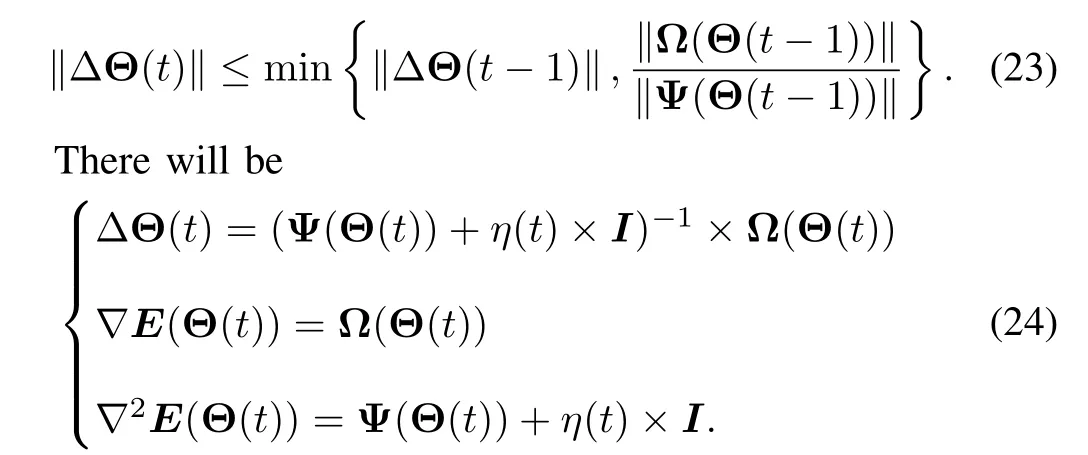
It follows from(23)and(24)thatΔV(Θ(t))can be expressed as

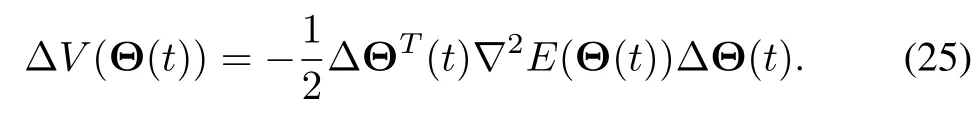
When the condition(21)is satisfied,the matrix∇2E(Θ(t))is positive definite,then we can conclude thatΔV(Θ(t))＜ 0.Therefore,

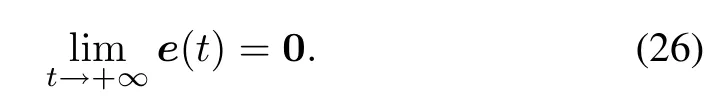
According to the Lyapunov stability theorem,we know that the DP-AFNN is convergent.

Fig.2.Schematic diagram of the modeling of EC and EQ.

V.SIMULATION STUDIES

A.Wastewater Treatment Process

The mostpopular technology of wastewater treatment is the activated sludge process(ASP).To evaluate the performance of different control strategies,a benchmark simulation platform based on ASP has been developed with the framework of COST Actions 682 and 624-BSM1[24].

In the BSM1,EC is the sum of aeration energy(AE)and pumping energy(PE).AE and PE are calculated as

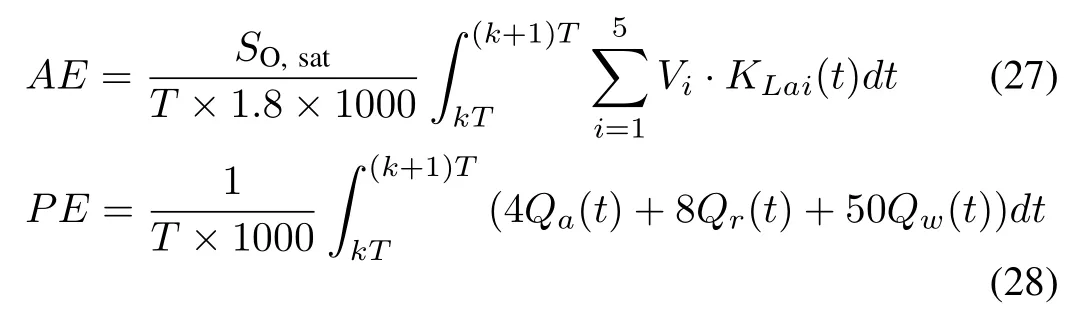
where KLaiand Viare the oxygen transferrate and volume of the i th biological reactor,respectively.SO,satis the saturation concentration of dissolved oxygen and T is the optimal cycle.Qa,Qr,and Qware the internal recycle flow rate,external recycle flow rate,and waste sludge flow rate,respectively.

Moreover,EQ is defined as

where S Seis the suspended solid concentration,C O Deis the chemicaloxygen demand,SNKj,eis the Kjeldahlnitrogen concentration,SNO,eis the nitrate and nitrite nitrogen concentration,B O D5,eis the biochemicaloxygen demand of 5 days,and Qeis the effluent flow rate.

In the BSM1,there are two control loops.One is the control loop of the dissolved oxygen concentration(SO,5)in the fifth reactor and another is the control loop of the nitrate level(SNO,2)in the second reactor.The manipulated variables for SO,5and SNO,2are KLa5and Qa,respectively.Through the analysis of the reaction mechanism and optimal control,Qw,KLa3,KLa4,SO,5,and SNO,2are selected as the decision variables.The aim of multiobjective optimal control in the WWTP is to acquire the balance between EC and EQ with the usage of the best set points of decision variables found by the optimization algorithm.Thus,any attempt to develop the models of EC and EQ is not trivial.In this study,the proposed DP-AFNN method is adopted to establish the relationship between EC,EQ and decision variables.The schematic diagram of the modeling of EC and EQ is shown in Fig.2.The ranges of decision variables are listed in Table I.And Fig.3 demonstrates the changes of decision variables in an optimal cycle.

TABLE I THE RANGE OF DECISION VARIABLES

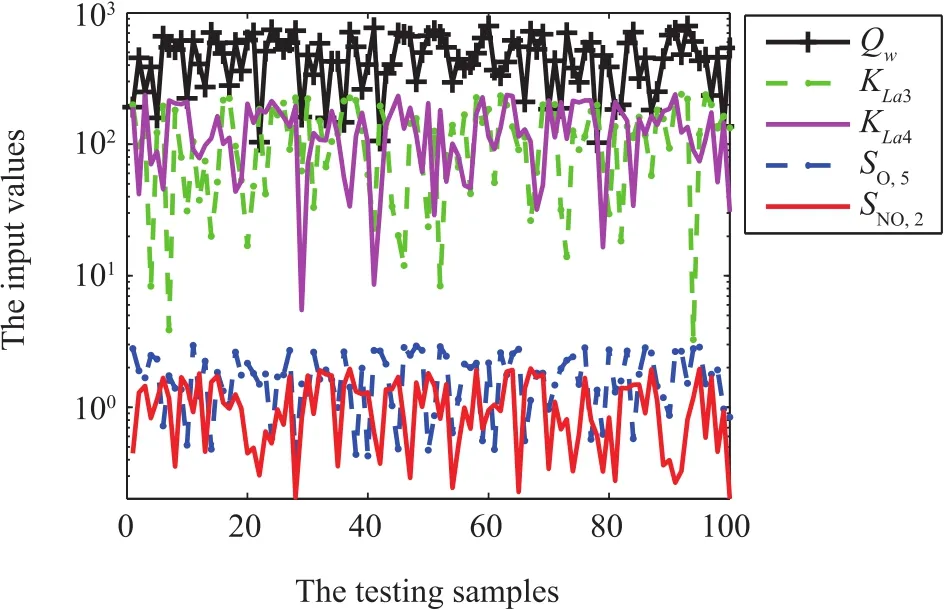
Fig.3. The values of input variables in the predicting process.

B.Experimental Settings

In this section,the effectiveness of the proposed DP-AFNN data-driven modeling method is demonstrated by using the BSM1 platform.A total of 500 samples are collected from BSM1.The preceding 400 samples are chosen as the training set,and the remaining 100 samples are applied as the testing set.Through the practicaltest,the parameters of DP-AFNN are setas follows:α%=2.5%,N=10,T=500.Regarding the number of input and output variables,two prediction models with the initialnetwork structure of 5-50-10-1 are constructed to predict EC and EQ,respectively.In the EBP algorithm,the learning rateηis set to be 0.01.

To assess the performance of the proposed DP-AFNN,the root mean-square-error(RMSE)and the predicting accuracy are adopted as two performance criteria in the experiments.For comparative analysis,the obtained results of DP-AFNN are compared with some existing methods,including modelbased and FNN-based methods.All the results are averaged on 30 independent runs.RMSE and Accuracy are defined as

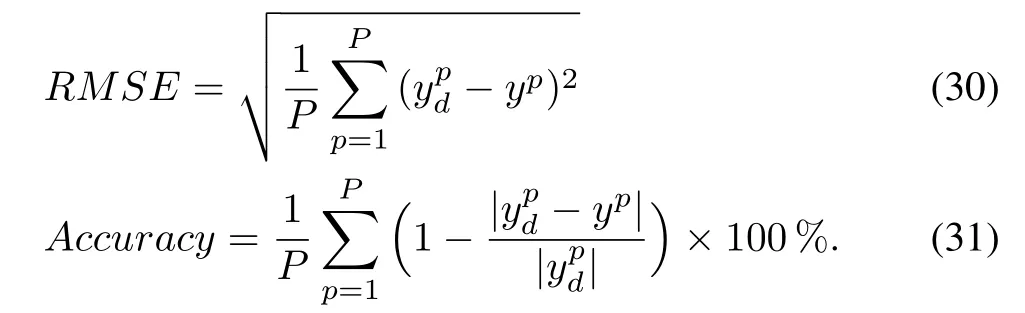
C.Experimental Results

1)Energy Consumption Modeling

For the EC modeling,Fig.4 shows the plotofγsorted in a descending order.From Fig.4,ten data points with highγare selected as clustering centers.Fig.5 presents the variation of RMSE values in the training process.From Fig.5,the RMSE values of DP-AFNN and FNN-EBP can converge to a steady state,but the convergence speed of DP-AFNN is obviously faster than FNN-EBP.One may notice that the integration of the DP-based structure identification and adaptive parameter learning algorithm can achieve better solutions.The predicting results of the EC values are shown in Fig.6,and the graphs of predicting errors between the desired and predicted outputs of these two algorithms are displayed in Fig.7.From Fig.7,the predicting errors obtained by the proposed DP-AFNN model are smaller than that of FNN-EBP.

Fig.4. The value ofγin decreasing order.

Fig.5.RMSE values during training.

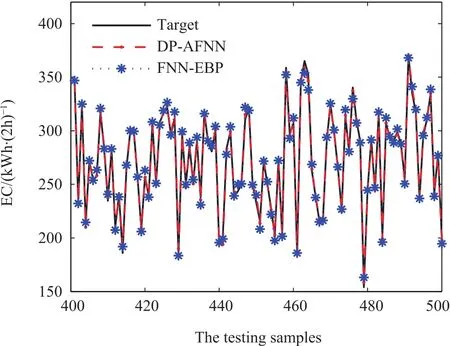
Fig.6. The predicting values of EC.

The performance of the proposed DP-AFNN for EC modeling is compared with the FNN-EBP,BSM-MBR[25],TCIM[26],MLR[27],ARKF[10],and DFNN[15].The details of performance comparison are given in Table II.As observed in Table II,the proposed DP-AFNN achieves the smallest testing RMSE(0.97)and the best testing accuracy(99.39%).The performance of DP-AFNN is superior to that of FNN-EBP and other mechanism methods.Although the MLR gets the least training time(0.03 s),its testing accuracy(95.17%)is lower than that of DP-AFNN.The comparisons indicate that the proposed DP-AFNN algorithm can be utilized to address the EC modeling problem in the WWTP.

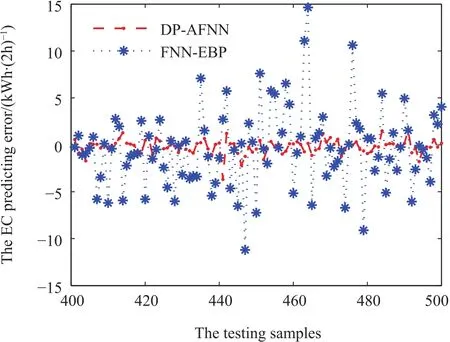
Fig.7. The predicting error of EC.

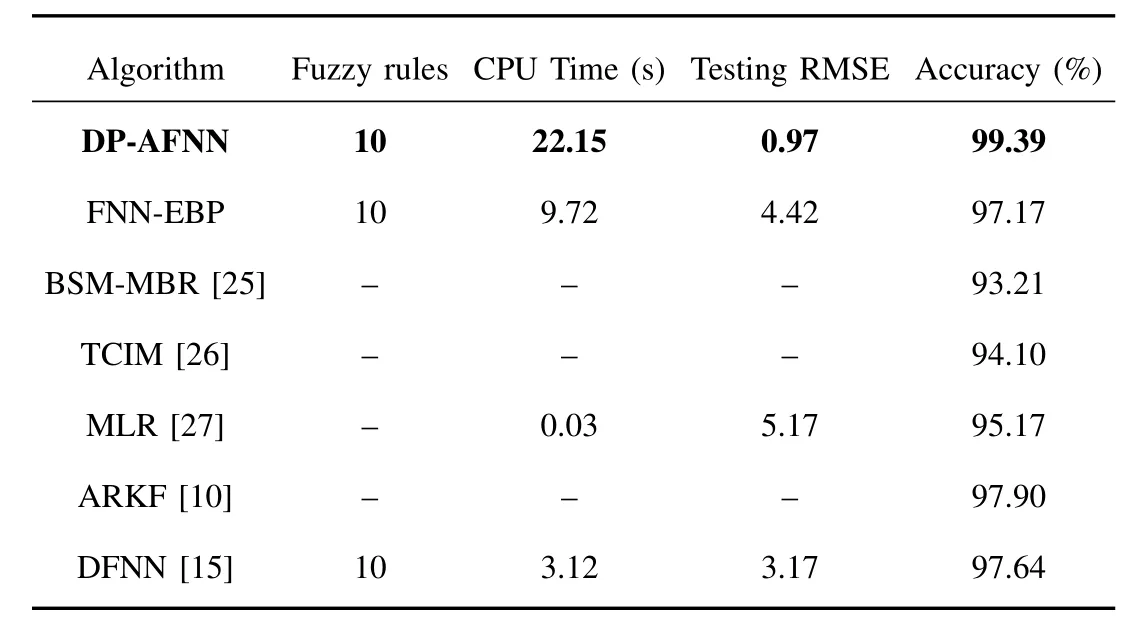
TABLE IIPERFORMANCE MEASURE VALUES OBTAINED BY DIFFERENT ALGORITHMS FOR EC

2)Effluent Quality Modeling

For the EQ modeling,the variation of RMSE values in the training process is presented in Fig.8.Based on the results shown in Fig.8,the proposed DP-AFNN method achieves faster convergence speed than that of FNN-EBP.The predicting results of the EQ values are shown in Fig.9,and the graphs of the predicting errors between the desired and predicted outputs are displayed in Fig.10.The predicting values demonstrate that the proposed DP-AFNN has high modeling precision.

The performance of the DP-AFNN for EQ modeling is compared with the FNN-EBP,MLR[27],and DFNN[15].The detailed results of different algorithms are exhibited in Table III.The testing RMSE and accuracy of the proposed DP-AFNN modelapproach to 0.96 and 93.04%,respectively,which is remarkable in comparison with other results.The experimentalresults in Table IIIdemonstrate thatthe proposed DP-AFNN has high generalization performance.

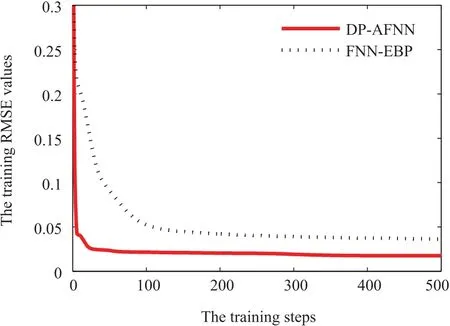
Fig.8.RMSE values during training.

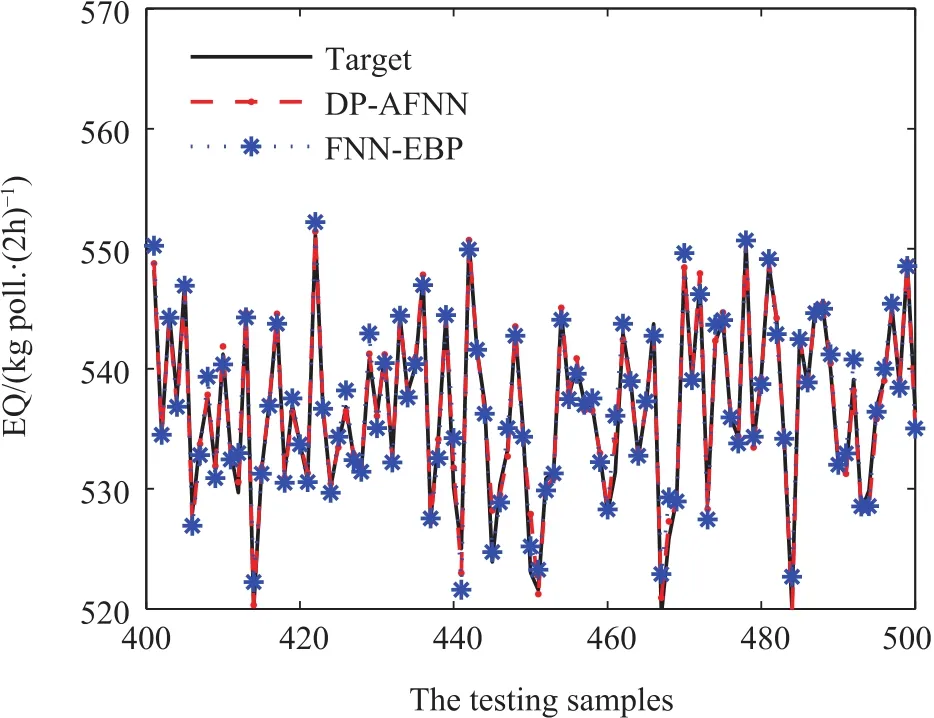
Fig.9. The predicting values of EQ.

Fig.10.The predicting error of EQ.

TABLE IIIPERFORMANCE MEASURE VALUES OBTAINED BY DIFFERENT ALGORITHMS FOR EQ

VI.CONCLUSION

In this paper,the DP-AFNN approach for designing the models of EC and EQ in the WWTP has been presented.The proposed method is technically developed with the usage of the DP-based clustering algorithm and the improved LM parameter learning algorithm.Based on the results obtained from the modeling of EC and EQ,the main contributions of this paper include:1)Since the DP-based clustering algorithm can partition the input space well,the initial fuzzy rules of the proposed DP-AFNN are suitable for all the training samples.The simulation results indicate that the DP-based fuzzy rules extracting method can also reduce the computationalcomplexity and enhance generalization ability.2)Since the parameters are optimized by using the improved LM algorithm,the convergence speed and learning ability of the proposed DP-AFNN are superior to that of the FNN-EBP.3)The experimentalresults indicate thatthe proposed DP-AFNN achieves bettermodeling accuracy than the mechanism models(i.e.,BSM-MBR and TCIM)and other FNNs(i.e.,FNN-EBP and DFNN).4)The experimentalresults also demonstrate that the EC and EQ models in the WWTP can be developed with acceptable accuracy utilizing Qw,KLa3,KLa4,SO,5,and SNO,2as decision variables.

This work,which has solved the modeling problems of EC and EQ,plays an extremely essential role in the subsequent study of the multiobjective optimal controlin the WWTP.The following work of our team includes two aspects.One is to dealwith the complicated multiobjective optimization problem with the usage of the multiobjective evolutionary algorithm.The traditional multiobjective evolutionary algorithm should be improved so that high-quality Pareto optimal solutions can be found.The other is to design two tracking controllers for the optimal set-points of SO,5and SNO,2.The built-in PID closed-loop controllers of BSMshould be improved in orderto achieve higher tracking accuracy and better control placidity.