A Robust Reserve Scheduling Method Considering Asymmetrical Wind Power Distribution

Guanzhong Wang,Qiaoyan Bian,Member,IEEE,Huanhai Xin,Member,IEEE,and Zhen Wang,Member,IEEE

Abstract—Nowadays,limited predictability and controllability of wind power are regarded as some bottlenecks to wind generation integration with the power system.This paper introduces a robust reserve scheduling method,where the spinning reserve allocation among conventionalunits is considered as well.The method applies to asymmetrical wind power distribution,and offers control on the degree of solution’s conservatism by changing the robustness budget.Meanwhile,distributional information of wind power is represented by mean value and asymmetrical bounds.Furthermore,the model is converted into a deterministic programming problem with dual theory.Case studies for asymmetrically distributed wind power illustrate its effectiveness.

I.INTRODUCTION

B Y the end of 2013,the installed wind capacity in China has been the largest in the world,and the wind has become the third-largestelectricalpower source in China[1].On the other hand,limited predictability and controllability of wind generation due to its intermittent characteristics still affect the quality of its power supply[2].To enhance the reliability of power system operation under fl uctuant load and wind power,spinning reserve(SR)provided by thermal generators needs to be scheduled.As the penetration of wind generation increases rapidly,it is of great importance to explore more reliable and economic strategies to address wind power uncertainty in reserve scheduling problem[3].

The reserve scheduling with wind generation integration has been well studied in many literatures,in which those methodologies can be classified into three categories:the deterministic reserve margin methods(DRM),the stochastic optimization(SO)and the robust optimization(RO).As of DRM,the reserve capability is usually evaluated based on the possible largest forecast error of real-time wind power output[4],[5].However,it is very diffi cult to determine the representative operation condition for DRM-based decision-making.As an improvement,SO can consider more complicated operating conditions than DRM with certain assumption of wind power probability distribution given.For instance,in[6]a Beta function is used to fit the distribution of real-time output of wind farms;in[7]a chance-constrained optimization model is proposed to compute the reserve requirement;Weibull distribution of wind speed is used to obtain the probability distribution of wind generation output in[8].However,there exist two SO’s disadvantages:1)SO problem above usually is a non-convex optimization problem which poses optimal solution diffi culty[7];2)accurate evaluation of probability distribution is hard in some real situations[9].

From another aspect,in recent years the RO-based approaches have attracted considerable attention for their probability distribution-free advantages[10]-[25].As a branch of RO methods,the robust linear optimization(RLO)is a convex optimization and can well control the degree of solution’s conservatism[10]-[15].The method of RLO has experienced severalevolutions since Soysterfirstdeveloped the RO method in 1973[12].To address the RO’s over-conservatism problem,Ben-Tal and Nemirovski introduced a robust linear optimization,where the rows of the constraintmatrix belong to some ellipsoid uncertainty sets and the robustcounterpartis a secondorder cone programming[13].To overcome the numerical calculation difficulty,an improved RLO method was proposed in[14],in which a linear robust counterpart is developed.However,all above RLO methods considering distributional information assume that the uncertainty of random variables is symmetrical with respect to the mean value.To handle the uncertainty asymmetry,Kang further proposed an RLO method called Kang’s robustlinear optimization(KRLO)[15].

To our best knowledge,the existing RLO-based reserve scheduling methods have not included the research on asymmetrical wind power with respect to its mean value,e.g.,[26]uses wind power interval without mean value;[27] considers symmetrical wind power distributional information,which indicates the up-spinning reserves and the down-spinning reserves may have the same distribution interval.However,wind power may be asymmetrical distributed in some cases[6]-[9].In this paper,a robust reserve scheduling method is introduced to pursue the minimum spinning reserve cost,in which spinning reserve allocation as an additional AGC (automatic generation control)functionality is achieved by a linearization decision rule.This KRLO-based method applies to asymmetrical wind power distribution,and can control the degree of solution’s conservatism by an adjustable robustness budget.Meanwhile,the wind power uncertainty is represented by an asymmetrical uncertainty set of KRLO with given mean value and maximum/minimum limits.The robust counterpart handling of KRLO,which is based on dualtheory,can convert the proposed model into deterministic formulations.

The rest of the paper is organized as follows.In Section II,the mathematical formulation of reserve scheduling is introduced.The KRLO method and the solution framework are presented in Section III.Numericalexamples are provided in Section IV.And Section V concludes the paper.

II.MATHEMATICAL FORMULATION

A.Problem Description

The following assumptions are made for problem formulation:1)only wind power uncertainty is considered and bus loads are regarded as well-forecasted;2)each wind generator is connected to the transmission network from a single bus;3)wind powercan be asymmetrically distributed;4)a standard DC power flow is used[28];5)unit commitment solution has been solved in advance.The firstand second assumptions are common in the reserve scheduling problem.The third assumption is more practical compared with those symmetricaldistribution cases.The fourth is based on a fact that in a transmission network the active power is mainly phase angle related and reactive poweris voltage magnitude related.Under normal condition,voltage magnitude variation is small and a DC power flow can be considered in transmission network[28].The last assumption ensures that the state of units has been determined before reserve scheduling.

Spinning reserve serving to AGC is allocated to each participating generator according to some distribution vector,ddd=[d1,...,dn]T,Pidi=1[29].In this paper,the distribution vector ddd is to be determined for AGC service in reserve scheduling stage.The existing AGC loop is illustrated in Fig.1,in which frequency regulation reserves are allocated based on the KRLO method.

Fig.1. Schematic diagram illustrating the AGC functionality required for the proposed reserve scheduling method.

B.Reserve Scheduling Model

The reserve scheduling aims to reduce the procurementcost of generation and reserves.The following linear costobjective function is adopted[26],

where CCCg,CCCup,CCCdown∈Rnare the costcoefficientvectors of generation,up-spinning reserves,and down-spinning reserves,respectively.PPPGdenotes the generation dispatch results;RRRup,RRRdown∈Rnare respectively up and down spinning reserves to be determined;N is the number of nodes in the power system.Notice that,a few elements in the vectors may be zero,i.e.,if there are no generators atnode i(i＜N),the i th element of PPPGis equal to zero.Constraints are as follows:1)Nodal power balance:

where BBB ∈ Rn×ndenotes the nodal admittance matrix of transmission network;θ∈ Rnrepresents the phase angle vector;gggsand gggfcorrespond to the scheduled output vectors of output-fixed units and spinning reserve units,respectively,and gggs+gggf=PPPG;Δgggfrepresents the power compensation for the real-time mismatch;pppwand pppddenote the wind power vector and the load vector,respectively.

2)Wind power limits:

Responding to the time scale and practical demand in engineering,the random variable PPPwcan be divided into two parts:the forecasted mean value and the uncertain deviation:

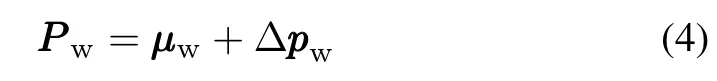
whereµwrepresents the mean value of wind power;Δpppwdenotes the uncertain deviation between the real-time output and the mean value.Moreover,-ωB≤ΔPPPw≤ωF,in which

whereωFand-ωBdenote the upper and lower limits of deviation respectively.IfωB/=ωF,the wind power distribution is called asymmetrical.

3)Generation limits:

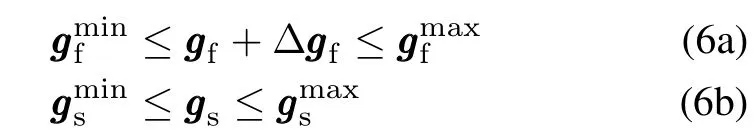
4)Spinning reserve allocation:

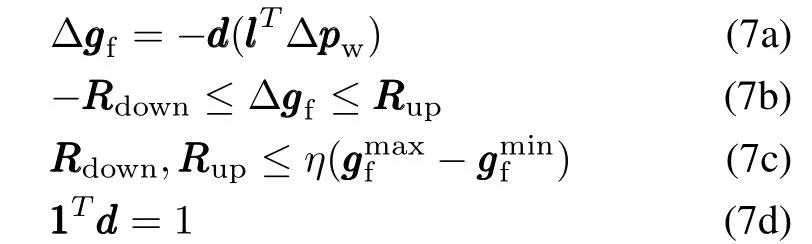
where 111 denotes a vector where all the elements are one;the element of ddd is zero if corresponding to an output-fixed unit,otherwise,it is a decision variable corresponding to an SR unit;the linearization decision rule in[11]is introduced to demonstrate the reserve allocation for the wind power deviation(7a);constraints(7b)and(7c)indicate that SR should be within the ramp rate limits,which correspond to the limitofgeneration compensation;moreover,the lastconstraint(7d)ensures the power mismatch can be fully compensated.

5)Transmission capability constraints:

where FFF is the branch power flow vector;TTT denotes the admittance matrix of network branches[30];fffmaxdenotes the deterministic transmission capacity limits.Since the uncertain wind power is included in constraints(2)that share the same nodal phase angle vectorθwith(8),the branch power flow vector FFF is also uncertain.Constraints(8)and(9)can guarantee that the standard transmission limits will be respected under uncertain wind generation.

In the model,decision variables are PPPG,RRRup,RRRdownand ddd;uncertain vector isΔpppw;Δgggfandθare adjustable variables;the rest are parameters.

Considering SR allocation and transmission capability constraints,the reserve scheduling with uncertain wind power,as an additional AGC functionality[30],is provided.The operating controller may monitor the deviation of the wind power and use the distribution vector ddd(see Fig.1),as a lookup table,to allocate the SR.

The reserve scheduling problem in(1)-(9)is a special linearprogramming problem with wind poweruncertainty embedded,which will be handled by the tractable reformulation below.

III.TRACTABLE REFORMULATION

A.KRLO With Asymmetric Data Uncertainty

For a general linear optimization model considering uncertain data:

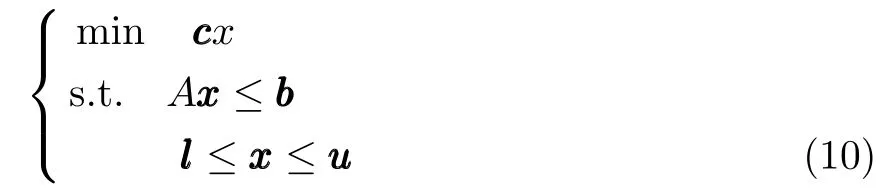
where xxx∈Rnis the decision variable;uu,,,lll ∈Rndenote the upper and lower bounds of xxx;ccc∈Rnis the coefficient vector;bbb∈Rmis a deterministic vector.And we assume that uncertain data only affects the elements in matrix A∈Rm×n[15].

RLO was proposed to find a solution of(10)immune to the uncertain data in[14].RLO methods are based on the following notation.The elements of A are denoted byi=1,...,m,j=1,...,n;the mean value of aijis;moreover,the uncertain data in different inequality constraints are assumed to be independent of each other.Letrepresents the set of uncertain data in row i of matrix A,and|Ji|represents the number of elements in set Ji.

Studies in[14]and[26]are both based on the assumption that=,which means the uncertain data are symmetrically distributed.Although the uncertainty set and robust counterpart in[14]and[26]could be used in reserve scheduling with uncertain wind power,they cannot be applied when the wind power is asymmetrically distributed[6]-[9].

To handle the asymmetricaluncertainty where/=,we introduce the KRLO uncertainty set with a robustness budget Γi(Γ ≤ |Ji|)[15],which can be defined as:

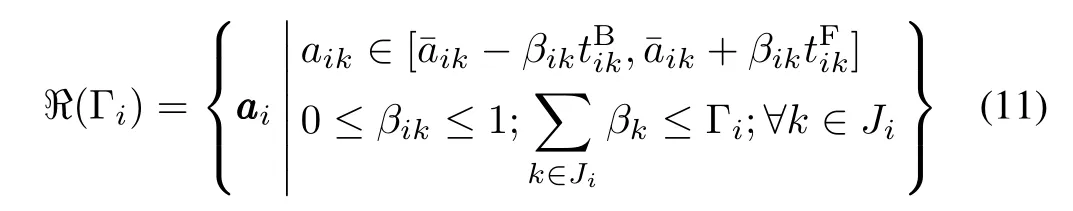
where aaaidenotes the uncertain data vector in row i of matrix A,i=1,...,m;βikdepends on the robustness budgetΓi,which serves to adjust the conservative level of ℜ(Γi),i.e.,the larger the value of Γiis,the more robust ℜ(Γi)will be.Obviously,ℜ(Γi)could also denote symmetric uncertainty when=.

With dual theory,the robust counterpart of(10)and(11)can be given in(12):

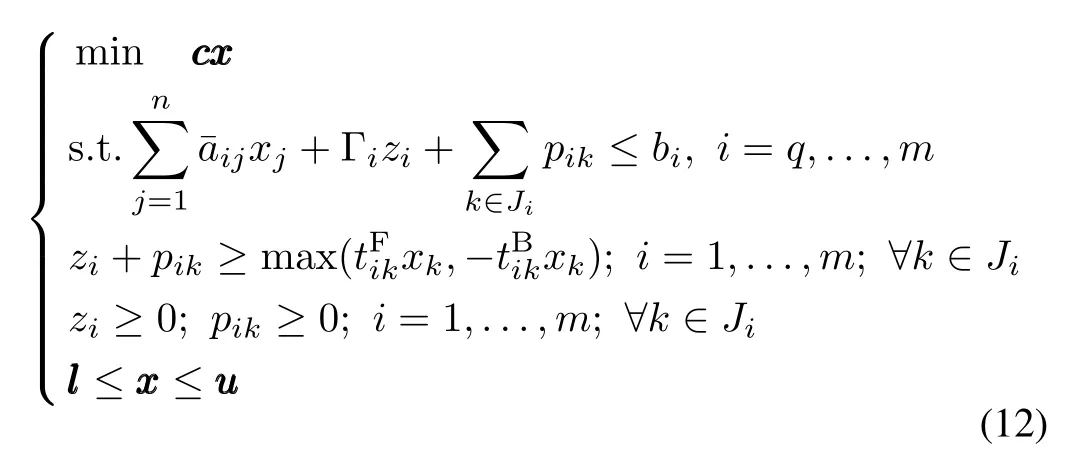
where ziand pik(i=1,...,m,∀k ∈ Ji)are auxiliary variables with no actualphysicalmeaning[15].The robustcounterpart(12)is a determined linear programming.By increasing Γifrom Γi1to Γi2(Γi1≤ Γi2),the conservativeness level of the solution withΓi1will be lower than that withΓi2.

By introducing the robust counterpart,the nominal linear programming is converted into a deterministic formulation.The robust counterpart(12)has the same optimal solution with the nominal linear programming(10)when the solution is immune to the uncertainty of(11),which is proved in[15].

B.Robust Reserve Scheduling

This section serves mainly to achieve the decoupling between the decision variables and uncertain variables in the equality constraints(2),and convert the optimization model into the general form(10).

1)Variables Simplification

Nodal phase angle vectorθserves as a redundant variable and can be eliminated only by substituting the equality constraints(8)to the power balance constraints(2).We use the linear sensitivity matrix between branch power flow and nodal injection power[11]in further detail to take the place of-BBB T-1.Then,the equality of nodal injection power and branch power flow is obtained:

where S denotes the linear sensitivity matrix.

The power balance constraint covered in equality(13)can be formulated as

where IB,UB,WB and LB respectively denote the sets of output-fixed unit buses,spinning reserve unit buses,wind generator buses and load buses,respectively.

Further,by substituting equality constraints(13)to the transmission limit constraints(9),inequality constraints with uncertain wind power are obtained:

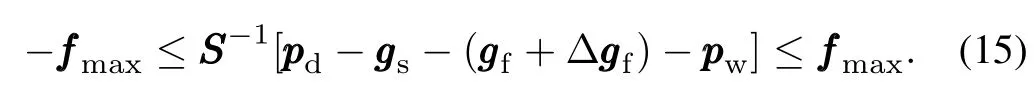
So far,the equality constraint with uncertain variables(2)is converted into the equality(14)and inequality(15)without nodal phase angle vectorθ.

2)Deterministic Constraints

Notice thatthere are no equalities with uncertain data in(12)and there are uncertain variables in equality(14).Therefore,to eliminate the uncertain wind power in(14),we substitute constraints(4),(7a)and(7d)to(14).And then,the equality with respect to the system power balance under wind power forecast is obtained:

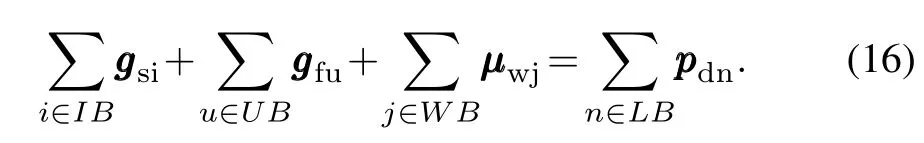
3)Inequality Constraints With Uncertain Wind Power

By integrating constraints(6a)-(6b),(7a)-(7d)and(15),we get the following inequality constraints with the only uncertain vectorΔpppw:

The uncertainty set of deviationΔpppwcan be written as follows:

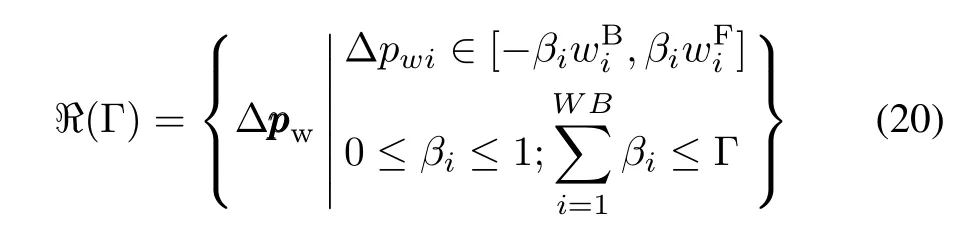
where the robustness budgetΓshould not be greater than the number of wind generators.According to the KRLO theory,constraints(17)-(19)can be converted into a robust counterpart similar to(12).

Thus,the reserve scheduling model(1)-(9)can be further converted into a deterministic programming problem that consists of linear equality/inequality constraints.

C.Algorithm Complexity Analysis

The optimization problem can be transformed into the robustcounterpart(12)automatically via the MATLAB interface YALMIP[30].The algorithm for the problem could be any common linear programming algorithm,which is embedded in many solvers,such as the CPLEX[31].Therefore,the algorithm in this paper is of polynomial time complexity and fast enough when wind generation changes.

IV.CASE STUDOES

In this section,a simulation analysis of varying robustness budget and ramp rate will be conducted with asymmetrical wind power distribution.In addition,this section also presents a comparison between KRLO method and an adjustable robust method with symmetrical wind power distribution.

A.Revised Garver’s 6-bus Test System

The revised Garver’s 6-bus system[10]is used to verify the effectiveness of the introduced approach.As shown in Fig.2,four wind farms are connected to the power grid from different buses.Parameters of the load(L1-L5),generators,wind farms,branches,and the cost coefficients are shown in Tables I-III,respectively.All of the thermal generators are engaged in the reserve allocation;pppddenotes the load;gggminand gggmaxdenote the lower and upper limits of units;nijdenotes the number of transmission lines between node i and j;xijdenotes the imaginary partofadmittance of each branch;fijcorresponds to the active power limit of one line between node i and j.

Fig.2.Configuration of modified Garver’s network.

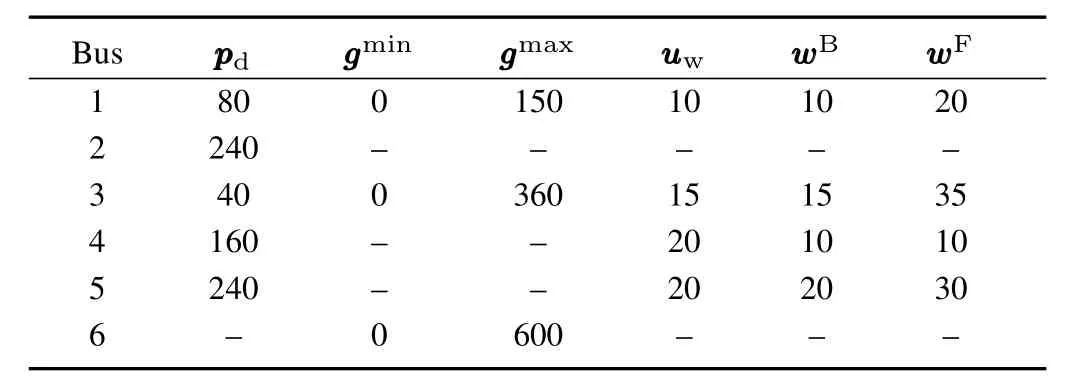
TABLE I SYSTEM BUS DATA(MW-1)

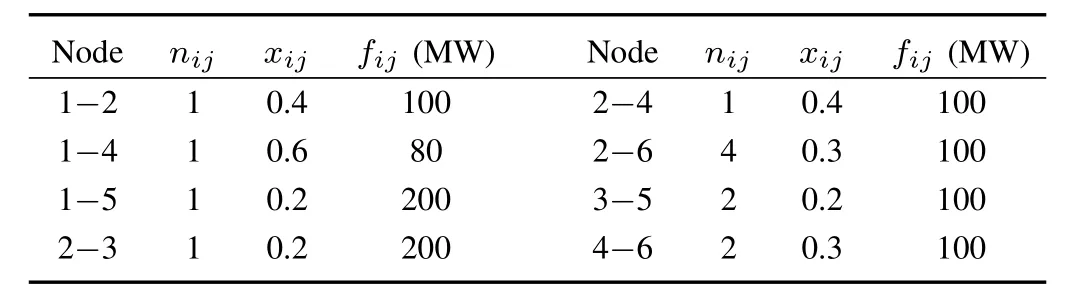
TABLE IISYSTEM BRANCH DATA

TABLE IIICONVENTIONAL GENENATOR COSTS($/MW)

The optimization is solved by the solver CPLEX in the interface YALMIP of MATLAB.

1)Effect of Robustness Budget

This case investigates the effect of the robustness budget.Fixed ramp rate parameterηis used to make this simulation.Results of Table IV show the variation of the total cost,and the total up/down spinning reserves withη=1/6 orη=1/4 when the robustness budgetdecreases.Respectively,Fig.3 and Fig.4 show the variation of the up/down spinning reserves provided by each participating unit withη=1/6 when the robustness budget increases.

As is seen in Table IV,the total cost of the generation and reserves with a fixedηreduces when the robustness budgetΓdecreases.The reason for the results is that the decreasing value ofΓleads to a lower fluctuation of wind power considered in the problem.In Fig.3 and Fig.4,unit 3 provides the largestreserve capacity for uncertain wind power in the 6-bus system,because the reserve capacity limit of unit 3 is much larger than those of other units and that reserve capacity limit of unit 1 is reached.

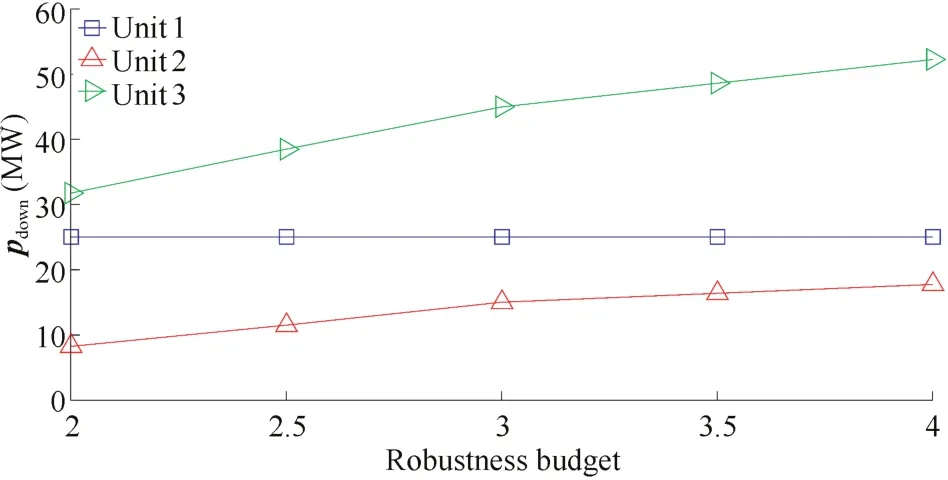
Fig.3.Down-spinning reserves provided by each unit(η=1/6).

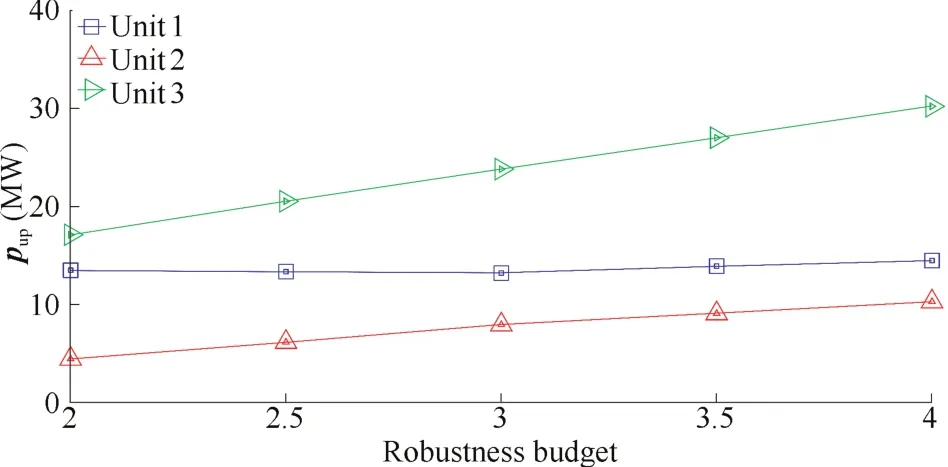
Fig.4. Up-spinning reserves provided by each unit(η=1/6).

2)Effect of Ramp Rate

This case considers the effect of the ramp rate.Fig.5 and Fig.6 show the up/down spinning reserves provided by each participating unit withη=1/4,respectively.

It can be seen from the comparison betweenη=1/6 and η=1/4 that a bigger value ofη,which corresponds to a larger ramp rate provided by participating units,will reduce the total cost in Table IV,and increase the reserves provided by unit1 in Fig.5 and Fig.6.The reason is thata larger ramp rate ensures the power mismatch can be compensated more by the optimal reserves purchased from unit 1,which is an affordable approach in this test system.

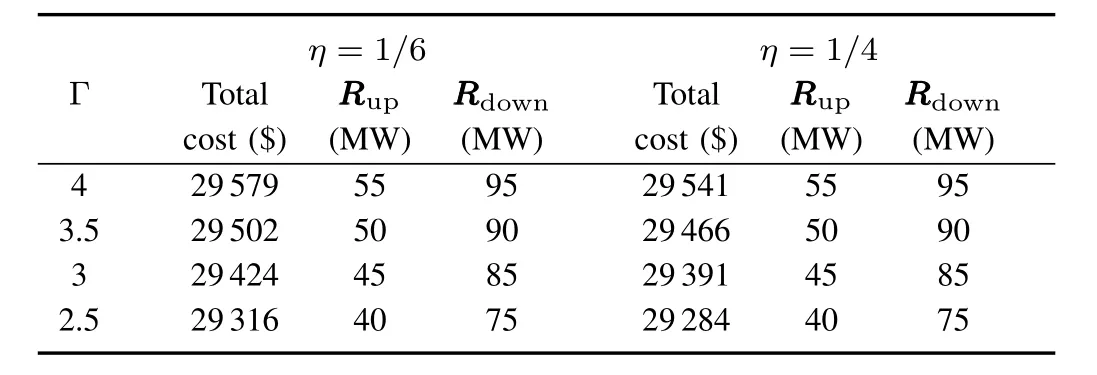
TABLE IV CONVENTIONAL GENENATOR COSTS($/MW)

Fig.5.Down-spinning reserves provided by each unit(η=1/4).

Fig.6. Up-spinning reserves provided by each unit(η=1/4).

In addition,the total up/down spinning reserves withη=1/6 are equalto those withη=1/4 in Table IV.The reason is thattotalreserves are determined by the worstcase fluctuation.As is seen in the powersystem,the totaldown spinning reserve required for the worst case is 95 MW where the robustness budget is 4(the number of wind generators),which presents the probable maximum deviation between the real-time output and the forecast output(the mean value).In other words,total reserves are determined by the parameterΓ,but the distribution vector can reflect the influence of other factors,such as ramp rate.

3)Comparison With an Adjustable Robust Method

This case investigates the differences between the KRLO method and the adjustable robust optimization(ARO)method of[26]with symmetric wind power.Based on the method in[26],each deviation of the wind generation belongs to an uncertain interval without robustness budget,i.e.,∈

By setting the wwwFequal to wwwBin Table I,symmetric wind power distribution is considered.Table V indicates that the solution obtained via the KRLO method is the same as the ARO method’s solution,when the robustness budget is 4.In conclusion,KRLO method applies to both symmetric and asymmetric uncertainty,and could control the solution’s conservatism only by changing the robustness budget;ARO method could also control the solution’s conservatism via changing the bounds of each deviation interval.

TABLE V TOTAL COST AND RESERVES(η=1/6)

B.IEEE 39-bus System

The IEEE 39-bus system is used to test the scalability of the method.Withoutloss of generality,itis assumed thatthree wind farms are connected with the test system at bus 16,23 and 26,respectively.The data of wind farms are listed in Table VI.The generators atbus 30,31,35 and 38 are assumed to provide SR and the power outputs of the other units are fixed.All other system data can be referred in[32].

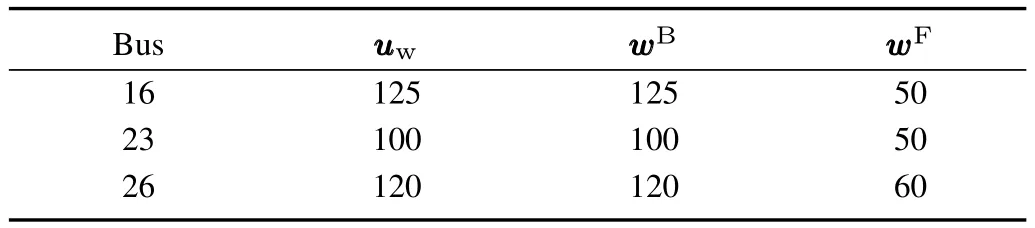
TABLE VI WIND FARM DATA

The total generation and reserve cost,total up spinning reserves and down spinning reserves are shown in Table VII.It can be seen that the cost and reserves increase with parameter Γbecoming larger.The reason is also that a larger value of Γmeans larger deviation of wind power considered in the reserve scheduling,then more SR will be purchased.

TABLE VII TOTAL COST AND RESERVE REQUIREMENT(η=1/6)

The allocations of up/down spinning reserves are shown in Fig.7 and Fig.8.In Fig.7,unit1 provides the maximum down spinning reserves,and the reserves increase with robustness budget being larger.The same situation occurs in Fig.8.

By comparison between the revised Garver’s 6-bus system and IEEE 39-bus system,the scalability of the method is illustrated.

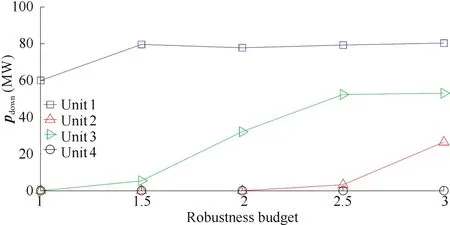
Fig.7.Down-spinning reserves provided by each unit(η=1/6).

Fig.8. Up-spinning reserves provided by each unit(η=1/6).

V.CONCLUSIONS

A robust method is proposed in this paper,as an analysis tool for reserve scheduling considering asymmetrical wind power distribution.This method can serve as an additional AGC function to allocate the SR with varying solution’s conservatism,and ramp rate.Simulation results verify that the approach is effective.

Besides,storage system will be helpful for the reserve scheduling problem,which will be our future work.On the other hand,this work is based on linear dual theory that has strong duality property,therefore,the robust counterpart is equal to the original problem.If the problem has non-affine constraints,the robustcounterpartis hard to obtain,which will serve as another future work of us.