正六边形钢管约束混凝土靶抗侵彻机理的数值模拟
2018-09-28蒙朝美蒋志刚宋殿义谭清华
蒙朝美, 刘 飞, 蒋志刚, 宋殿义, 谭清华
(1. 国防科技大学 基础教育学院,长沙 410072;2. 空军工程大学 航空工程学院,西安 710038)
混凝土广泛应用于遮弹结构[1],对混凝土施加约束可以有效提高其抗侵彻性能[2-3]。试验研究[4-7]表明钢管约束混凝土靶的抗侵彻性能优于无约束混凝土靶,但关于钢管约束混凝土抗侵彻机理研究不够充分。武珺等[8]进行了多边形钢管约束混凝土靶抗侵彻性能的数值模拟,表明正六边形钢管约束混凝土靶具有优异的抗侵彻性能;石少卿等[9-10]对仿生蜂窝遮弹层和钢管钢纤维混凝土遮弹层的抗侵彻性能进行了数值模拟,表明蜂窝状钢管的约束作用明显提高了遮弹结构的抗侵彻性能。蒋志刚等[11]利用ANSYS/LY-DYNA深入分析了圆形钢管约束混凝土的抗侵彻机理。但是,有些研究人员的研究对象是圆形钢管约束混凝土靶,与实际工程应用存在差异;还有些研究人员主要研究了多边形钢管约束混凝土靶的抗侵彻性能,但对抗侵彻机理的研究不够充分。正六边形钢管约束混凝土靶便于工程应用,深入研究其抗侵彻机理具有重要的理论意义和应用价值。
在上述研究的基础上,基于侵彻试验结果,运用ANSYS/LS-DYNA软件,采用有限元-光滑粒子法,对比分析了正六边形和圆形钢管约束混凝土靶的约束效应,揭示了正六边形钢管约束混凝土靶的抗侵彻机理。
1 仿真模型与试验验证
1.1 仿真模型
为了比较六边形和圆形钢管约束混凝土靶的抗侵彻性能,文献[12-13]进行了圆形和正六边形钢管约束混凝土靶抗侵彻试验,表明含钢率(钢管体积与靶体积的比值)为9.75%时,正六边形钢管约束混凝土靶的抗侵彻性能优于圆形钢管约束混凝土靶。试验弹丸为12.7 mm钨芯弹,结构如图1所示。质量48 g,长59.5 mm;其中钨芯直径7.5 mm,长34.3 mm,质量19.7 g。弹丸垂直入射靶心(实际偏心距小于10 mm),试验后钨芯变形很小,可视为刚体。圆形钢管为Q235无缝钢管,外径140 mm,壁厚3.5 mm;正六边形钢管由壁厚3.5 mm钢板焊接而成,边长80.5 mm,外接圆直径161 mm;所有靶厚350 mm。核心混凝土的实测密度为2 420 kg/m3,边长150 mm标准立方体抗压强度和劈裂强度分别为66.2 MPa和5.66 MPa,直径150 mm、高度300 mm圆柱体轴心抗压强度为54.3 MPa。

图1 弹丸结构图Fig.1 Structure of projectile
仿真模型按中心正入射处理,利用对称性取1/2结构建模。为了解决网格畸变问题,并有效模拟混凝土撞击成坑、碎片飞溅现象和体现钢管的约束效应,混凝土中心区域采用光滑粒子;同时考虑到计算效率,其他部分采用Lagrange网格。混凝土中心区域半径20 mm(约5倍弹径)范围内采用光滑粒子,共划分50 400个粒子;其他部分均采用Lagrange网格、SOLID164六面体实体单元,小变形区混凝土单元尺寸逐渐过渡,粒子附近的混凝土单元较细,钢管附近的混凝土单元较粗,正六边形靶的外围混凝土共划分146 160个单元,圆形靶的外围混凝土共划分126 000个单元;钢管沿厚度方向划分两个单元,共划分10 080个单元;靶的网格模型,如图2所示。弹丸按铜皮、钢套和钨芯建模,铜皮共划分750个单元,钢套共划分486个单元,钨芯共划分856个单元,网格模型,如图3所示。其中钨芯头部到铜皮头部的距离为25 mm。光滑粒子与弹丸间采用点面侵蚀算法,弹丸各组成部分间采用面面侵蚀算法,光滑粒子与混凝土有限元网格间采用固连点面接触,混凝土与钢管间采用面面接触。钢管侧面、靶体正面为自由边界,弹道剖面为对称边界,靶背面沿轴向位移为零。
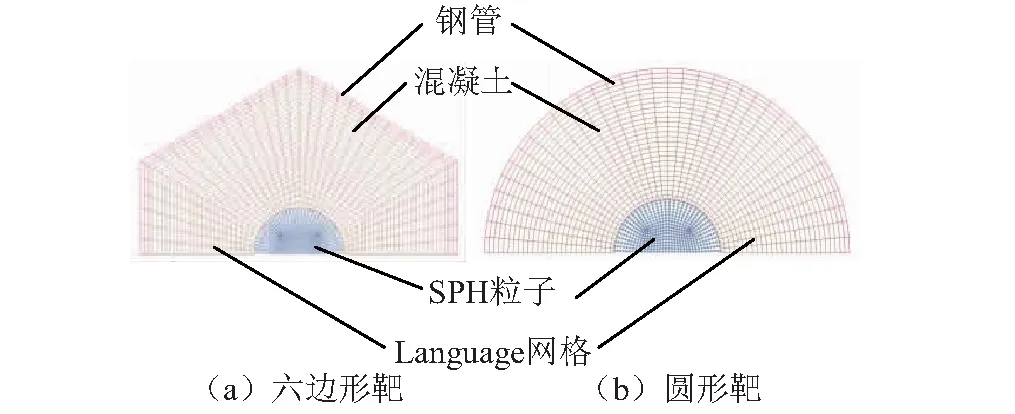
图2 靶的网格划分Fig.2 Finite element mesh of target
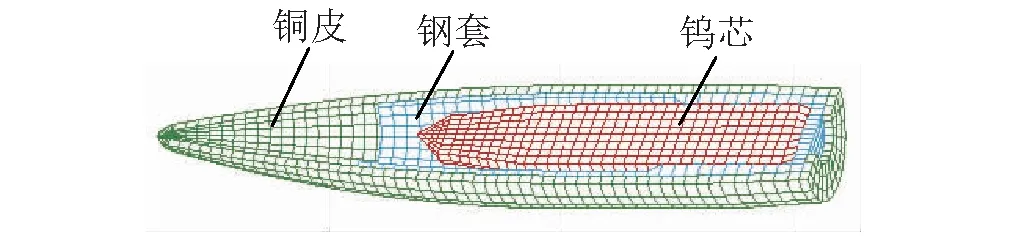
图3 弹丸网格划分Fig.3 Finite element mesh of projectile
根据弹丸材料的性能,结合侵彻试验结果,钨芯采用刚体(RIGID)材料模型,弹性模量360 GPa,泊松比0.25[14],密度取实测质量与体积的比值15 300 kg/m3;铜皮采用Johnson-Cook 模型,钢套采用随动硬化模型,参数都按蒋志刚等的研究采用。钢管为各向同性材料,且存在应变强化和应变率效应,采用随动硬化模型,主要参数如表1所示。
混凝土采用连续帽盖模型(CSCM_CONCRETE),主要参数如表2所示。其中粗骨料最大粒径按试验取为15 mm。帽盖模型[15]能较好地反应材料在冲击荷载作用下的非弹性响应,通过引入损伤变量对弹性模量和有效应力进行折减,即
(1)
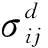

表1 钢管随动硬化模型参数
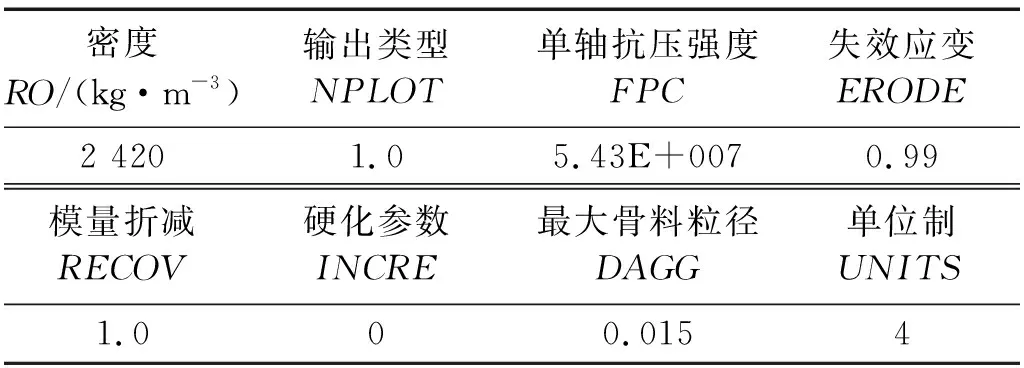
表2 混凝土帽盖模型参数
1.2 试验验证
图4和图5给出了相关文献中典型工况的试验结果(左图)与本文数值模拟结果(右图)的比较。其中:模拟结果为侵彻结束时的损伤(D值)云图,C140-2为圆形钢管,T161-13为正六边形钢管(图5(b)为过两对边中点所在剖面); Δd为试验偏心距,V0为撞击速度。

图4 混凝土侧面损伤模拟结果与试验对比Fig.4 Comparison between simulation and experiment of lateral concrete’s failure

图5 混凝土剖面损伤模拟结果与试验对比Fig.5 Comparison between simulation and experiment of cross-sectional concrete’s failure
由图4和图5可知:模拟结果与试验吻合良好,模拟结果(未考虑偏心的影响)的损伤云图基本对称,迎弹面有大量完全损伤的粒子飞离靶体,与试验中迎弹面成坑时混凝土碎片飞溅现象相吻合;混凝土表面损伤云图较好地体现了试验靶体的侧面裂纹分布情况。
表3给出了相关文献中典型工况侵彻深度模拟结果与试验结果的比较,由表3可知,两者吻合较好,最大误差为2.6%。
以上结果表明:本文仿真模型和材料参数合理,可用于研究六边形钢管约束混凝土靶的抗侵彻机理。

表3 彻深度模拟结果与试验比较
2 抗侵彻机理分析
为方便对比分析,正六边形(T161)和圆形(C140)钢管约束混凝土靶取相同的撞击速度820 m/s,弹丸中心正入射。
2.1 侵彻过程分析
图6给出了弹芯(刚性钨芯)的速度和位移时程曲线。可见:弹芯在C140和T161中的运动规律基本相同,当t<0.2 ms时,两条曲线基本重合,即钢管形状的影响很小;当t≈0.2 ms时,两条速度时程曲线开始分离,弹芯阻力大小开始产生较明显差异,但弹芯位移基本相同,约为125 mm,此时弹芯的侵彻深度约为100 mm(扣除弹芯头部至铜皮头部的距离25 mm)。
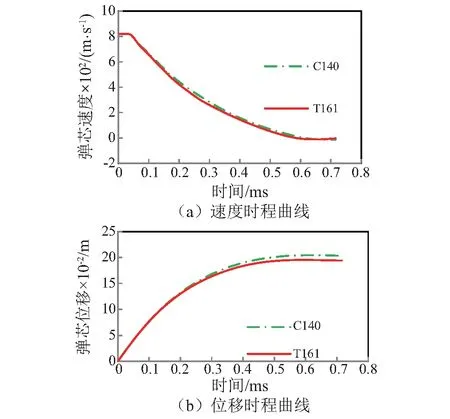
图6 弹芯时程曲线Fig.6 Time-history curve of projectile core
图7给出了C140(左图)和T161(右图)两种钢管约束混凝土靶剖面(T161为过对边中点所在剖面)和距迎弹面100 mm截面处典型时刻的混凝土损伤云图(D值)。

图7 混凝土典型时刻损伤云图(单位:mm)Fig.7 Damage of concrete at typical time(units: mm)
由图7可知,总体上T161和C140的混凝土损伤情况和损伤发展规律相似,均可分为开坑阶段和隧道侵彻阶段,但损伤模式存在差异。如图7(a)所示,当t<0.126 ms时,弹芯侵彻深度小于100 mm,钢管附近混凝土损伤较轻,钢管形状对混凝土损伤影响较小,此时迎弹面处的混凝土损伤基本已经完成,可认为开坑阶段结束。随着弹芯的不断侵入,应力波在钢管壁产生反射,当t≈0.2 ms时,如图7(b)所示,弹芯头部已到达距迎弹面100 mm截面,钢管附近混凝土产生了明显损伤,钢管形状对混凝土的损伤模式影响显著。其中,六边形靶损伤严重区域主要集中在各边的中部附近,这与侵彻试验后混凝土侧面裂纹分布规律相吻合。当t>0.2 ms后,如图7(c)和图7(d)所示,弹芯侵彻深度继续增大,直到侵彻结束;C140靶距迎弹面100 mm截面混凝土的损伤基本无发展,而T161靶距迎弹面100 mm截面的损伤仍有少量增加,即钢管形状对混凝土损伤仍有一定的影响。
综上所述,侵彻过程可分为开坑阶段和隧道侵彻阶段,钢管形状的影响主要发生在隧道侵彻阶段,且以弹芯头部扩孔阶段最为显著。
2.2 约束机理分析
由上述可知,钢管约束效应主要体现在弹芯头部扩孔阶段,这与相关文献的结果相吻合。为了分析粒子区外围混凝土和钢管对弹孔附近混凝土的共同约束作用,取光滑粒子与Lagrange网格界面处、距迎弹面100 mm截面的有限元单元进行分析。图8给出了典型单元的径向应力时程曲线(应力受拉为正,受压为负)。其中:C140为圆形靶对称面上单元;T161-1单元位于六边形靶对角线上,T161-2单元位于六边形靶过两对边中点剖面。
由图8可知,整体上,3条曲线的发展规律相似,但大小存在差异。当t<0.07 ms时,应力波尚未到达单元位置,3条应力时程曲线均呈水平状态;当0.07 ms
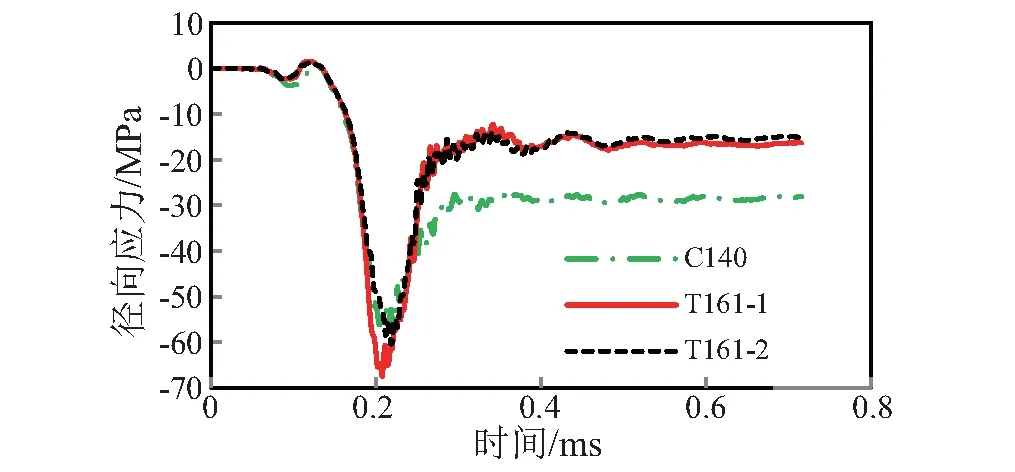
图8 单元径向应力时程曲线Fig.8 Radial stress time-history curve of elements
由上述分析可知,钢管的约束效应可分为应力波效应(弹头未到达前)和弹头扩孔阶段限制径向位移效应。为进一步分析钢管形状对弹头扩孔阶段约束效应的影响,图9给出了弹芯头部通过某一截面时该截面(距迎弹面100 mm截面)的等效应力云图。

图9 弹芯头部位置混凝土等效应力云图Fig.9 Effect stress of concrete at top of projectile
由图9可知,钢管形状显著影响弹芯扩孔阶段混凝土内应力的分布规律,圆形靶的等效应力呈轴对称分布,而六边形靶的等效应力在对角线附近形成了高应力区,小间距的高应力区增大了弹丸头部表面压力,从而增大了侵彻阻力。
为说明T161对角线附近形成高应力区的机理,提取了六边形靶距迎弹面100 mm截面处钢管单元(位置如图10所示)的应力时程曲线,如图11所示。图11(a)和图11(b)分别为钢管内壁单元沿Y方向和X方向的应力时程曲线,图11(c)为钢管外壁单元X方向的应力时程曲线。图10中,X轴与对角线平行,Y轴为过对边中点剖面,单元所在的边与X轴平行;单元T1位于过两对边中点的剖面,单元T6位于对角线上,单元T1~单元T6皆位于钢管内壁,与之相邻的钢管外壁单元编号为单元a~单元f。
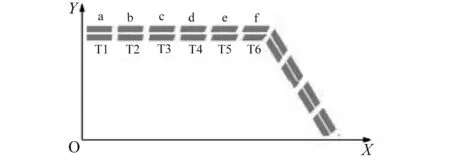
图10 钢管内壁单元示意图Fig.10 Elements of steel tube
由图11可知:①总体上,钢管壁沿边长方向应力分布不均匀,角部大,中间小;②钢管内壁Y向应力均为压应力,如图11(a)所示,应力大小从角部向各边中部逐渐减小;内壁X方向应力均为拉应力,如图11(b)所示,角部明显大于中部,且中部各点差异不大,即面内拉伸变形为主,弯曲应力小于面内拉伸应力;③钢管外壁X方向应力,如图11(c)所示。中部为拉应力,大小差异不大;角部为压应力,绝对值小于中部应拉力,即角部产生了内侧受拉、外侧受压的弯曲变形,这是对角线附近形成高应力区的原因。
综上所述,正六边形钢管约束混凝土靶的抗侵彻性能优于圆形钢管约束混凝土靶,其机理是:钢管壁受挤压作用,同时产生面内拉伸和面外弯曲变形,弯曲变形使角部钢管内侧受拉,角部径向位移小,增大了对混凝土的约束效应,混凝土对角线附近形成高应力区,小间距高应力区增大了弹头表面压力,从而增大了侵彻阻力。此外,应力波在钢管壁产生发射,反射波也会增大侵彻阻力。

图11 正六边形钢管单元应力时程曲线Fig.11 Stress time-history curve of hexagonal steel tube’s elements
3 结 论
本文采用光滑粒子与有限元相结合的方法,分析了12.7 mm钨芯弹侵彻圆形和正六边形钢管约束混凝土靶过程和机理,模拟侵彻深度和损伤模式与侵彻试验吻合较好,得到以下主要结论:
(1) 钢管约束混凝土靶的侵彻过程可分为开坑和隧道侵彻两个阶段,钢管的约束效应和形状的影响主要发生在隧道侵彻阶段,且以限制混凝土径向位移效应为主。
(2) 正六边形钢管约束混凝土靶的抗侵彻性能优于圆形靶,其原因为:弹芯扩孔时混凝土向外膨胀挤压钢管壁使正六边形钢管产生弯曲变形,角部内侧受拉,径向位移小,增加了对角线附近钢管对混凝土的约束效应,使得正六边形钢管约束混凝土对角线附近形成了高应力区,小间距的高应力区增大了侵彻阻力,从而提高了抗侵彻性能。
