基于结构与材料参数的S形薄壁梁抗撞性与轻量化研究

樊璐璐， 吉野辰萌， 林 烨， 刘 欢， 于征磊

(吉林大学 机械科学与工程学院，长春 130022)

汽车被动安全在汽车设计领域占有越来越重要的地位，提高汽车吸能部件抗撞性，尤其是前部主要吸能部件如吸能盒、前纵梁结构的抗撞能力对提高汽车安全性具有重要意义。目前，国内外学者主要通过引入新结构与新材料两种方式[1-2]来提高吸能结构的抗撞特性。一方面降低碰撞产生的峰值碰撞力，另一方面提高结构的吸能量，从而减小发生正面碰撞时汽车前部变形，降低对乘员的伤害。郝亮等[3]研究了薄壁锥形吸能盒结构在引入诱导槽设计后的吸能特性，并采用粒子群算法获得了既符合吸能要求又满足轻量化的简化吸能盒结构；Costas等[4]对钢与玻璃纤维复合材料的吸能结构进行多目标优化设计，大大提高了其抗撞能力。Tanlak等[5]基于几何形状尺寸优化，提高了圆形薄壁管在高速轴向碰撞工况下的抗撞性；Asanjarani等[6]探讨了基于诱导槽设计的变截面锥形结构的截面厚度、锥形角度、诱导槽数量及其半径对其抗撞性的影响。Hussain等[7]对比分析了多种诱导槽形式对玻璃钢圆筒形薄壁结构抗撞性的影响，得到了诱导槽的最佳位置分布。

针对S形薄壁梁结构的抗撞性设计问题，Kim等[8]从理论上推导了截面碰撞力与轴向位移之间的数学关系式，分析了截面的高宽比对碰撞力曲线的影响。Beik等[9]从理论上分析了变截面S锥形薄壁梁的碰撞力与结构尺寸的数学关系，并基于多目标优化算法进行抗撞性优化设计；Zhou等[10]研究了钢铝材料组合的S形前纵梁的抗撞性优化设计优势。Fang等[11]通过将钢制S形薄壁梁的前部材料更换为铝材，提高了抗撞能力，同时降低了结构的质量。从以上研究可见，合理的结构设计与材料选择不仅能够改善结构本身的吸能特性，还可以降低结构整体质量。

现有S形薄壁梁的研究基本针对原模型的结构几何尺寸，缺乏通过合理引入特征结构设计结合调整材料属性达到提高抗撞性与实现轻量化设计的目的。本文针对诱导槽与加强筋设计探讨了诱导槽的位置分布、数目及加强筋板的位置分布对方形截面S形薄壁梁抗撞特性的影响。基于快速多目标优化算法，对带有加强筋板的S形薄壁梁进行抗撞性优化设计，通过对比碰撞力-位移仿真曲线与理论曲线，验证了优化模型的有效性。进而通过改变优化模型的加强筋板材料，获得了满足轻量化设计要求且抗撞性明显提高的S形薄壁结构。

1 基于诱导槽与加强筋设计的薄壁梁结构模型的建立

1.1 方形截面S形薄壁梁空间模型的建立

本文以汽车前纵梁结构中常见的方形截面S形薄壁梁为研究对象，探讨在高速碰撞工况下，特征结构的位置分布及几何参数对其抗撞能力的影响。S形薄壁梁的空间简化模型及其几何形状尺寸，如图1所示。

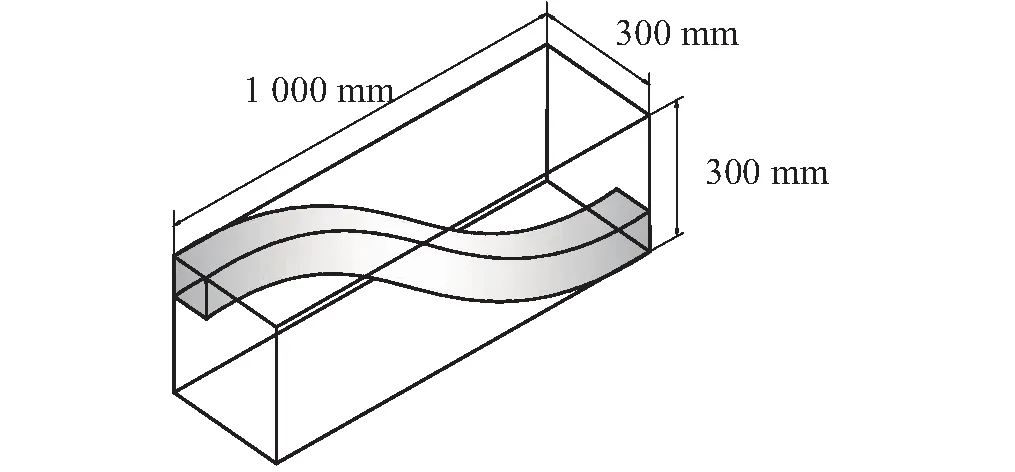
图1 S形薄壁梁的空间框架及尺寸Fig.1 S-shaped thin-walled beam: space-frame and size

前纵梁高速正面碰撞工况，通常采用刚性墙碰撞的方式给定，刚性板质量为1 000 kg，速度为v=10 km/h，如图2所示。前纵梁后端6个自由度全约束，前端约束5个自由度，只允许S形薄壁梁随刚性墙沿X轴方向移动。文中8种薄壁结构都采用同样的方式加载；材料采用低碳钢，材料密度为7 850 kg/m3,泊松比与杨氏模量分别为0.3与210 GPa。首先利用Hypermesh软件建立S形薄壁梁结构的有限元模型；随后，基于显式非线性有限元求解器Ls-dyna进行有限元碰撞仿真求解。

图2 S形薄壁梁的加载方式Fig.2 Impact condition for S-shaped thin-walled beams

1.2 基于诱导槽设计的S形薄壁梁有限元模型建立

按照有、无诱导槽和分布位置及其个数的不同，建立4种S形薄壁梁有限元模型，其局部放大示意图，如图3所示。这里，所有诱导槽尺寸规格相同。

图3 基于诱导槽设计的4种S形薄壁梁模型Fig.3 Four S-shaped models based on inducing grooves

图3(a)的原始方形截面S形薄壁梁结构记为模型O；图3(b)的前端设置一个诱导槽的结构记为模型A1；图3(c)的前后各设置一个诱导槽的结构记为模型A1-1；图3(d)的前端设置两个诱导槽的结构记为模型A11。

1.3 基于加强筋设计的S形薄壁梁模型建立

为了探讨引入加强筋设计对S形薄壁梁抗撞性的影响，在原S形薄壁梁结构的内部，添加了加强筋。根据加强筋位置和尺寸的不同(板厚相同)，建立4种简化模型，分别如图4(a)～图4(d)所示。图4(a)模型从前端～末端1 000 mm均添加了加强筋板，记为模型B；图4(b)模型仅在前端添加300 mm长的加强筋板，记为模型B1；图4(c)模型在中间400 mm部分添加了加强筋板，记为模型B2；图4(d)模型仅在后端添加300 mm长的加强筋板，记为模型B3。

图4 基于加强筋设计的4种S形薄壁梁模型Fig.4 Four S-shaped models based on stiffener

2 8种S形薄壁梁结构的抗撞性分析

在汽车碰撞过程中，通常把降低峰值碰撞力Fmax、 提高吸能量Ein和比吸能(Scale Energy Absorption，SEA)作为吸能部件具有较好抗撞能力的主要评价标准。在通过结构设计提高前纵梁抗撞性的过程中，保证结构强度和抗撞性的同时，期待结构总质量越小越好。本文“1.2”节与“1.3”节建立的8种S形薄壁梁模型，其对应的4种性能指标，如表1所示。为了更清晰地展示8种模型的各性能指标相对于原模型的变化情况，特分析了各性能参数的变化率，如表2所示。

表1 8种S形薄壁结构的性能指标对比

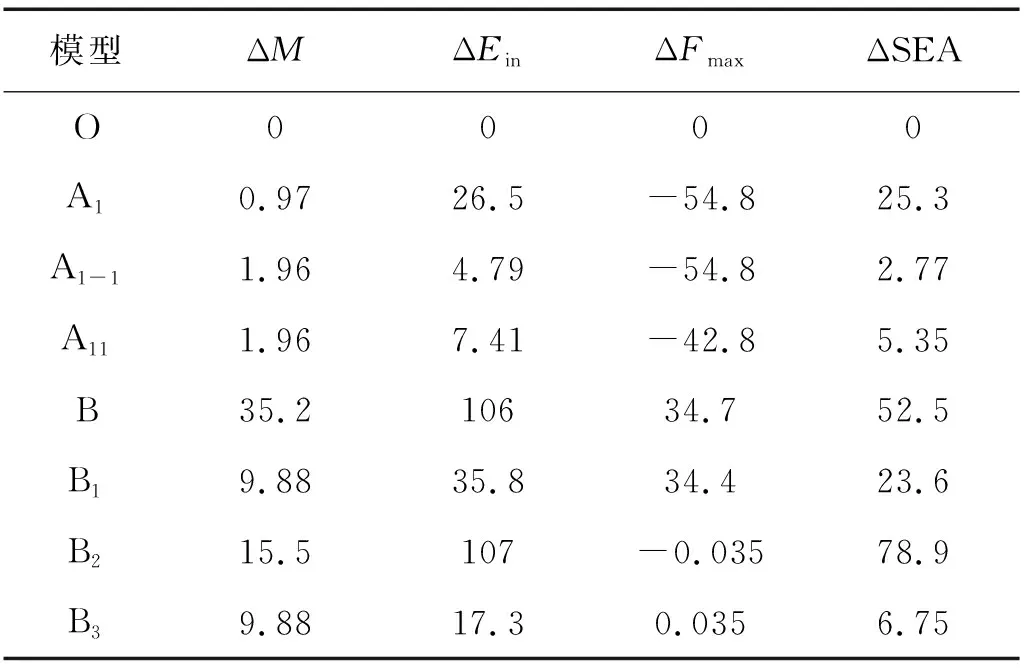
表2 各性能参数的变化率

由表1可知，无论是在薄壁梁上设置诱导槽，还是在其内部添加加强筋均会使结构总质量有所增加。由表2可知，基于诱导槽设计的3种模型A1，A1-1与A11的峰值碰撞力Fmax比原模型O分别降低了54.8%，54.8%与42.8%； 吸能量Ein分别提高了26.5%，4.79%与7.41%； SEA分别提高了25.3%，2.77%与5.35%。 特别是模型A1在总质量仅增加0.97%的情况下，Fmax降低了54.8%，Ein与SEA分别提高26.5%与25.3%。综合分析可知，通过引入诱导槽提高S形薄壁梁抗撞性的3种模型中，在薄壁梁前部设置一个诱导槽的模型A1比其他两种方式更有优势。

由表1、表2可知，在薄壁梁内部添加加强筋的4种结构中，模型B虽然吸能量提高了106%，但其峰值碰撞力增加34.7%，且质量增加35.2%，这不符合提高抗撞性与轻量化设计要求，模型B1亦然。模型B2与B3在保证碰撞力几乎不变的情况下，吸能量和比吸能均有提高，其中模型B2的吸能量提高107%，比吸能提升了78.9%。以上分析可知，引入加强筋设计的4种结构中，仅在薄壁梁中间弯曲部分添加加强筋板的模型B2综合性能最优。

综合考虑峰值碰撞力Fmax、 吸能量Ein与SEA等3个方面， 模型A1与模型B2的抗撞性均优于其他模型，但两者质量均有增加，不符合结构的轻量化设计要求。模型A1与B2在碰撞历程中某时刻的变形情况，如图5所示。两者与原结构O的碰撞力-位移曲线的对比情况，如图6所示。由图5可知，模型B2的变形大于模型A1，即B2的吸能量要大于模型A1； 由图6结合表1、表2可知，模型A1与B2的最大碰撞力Fmax均低于原模型O。因此，本文选取模型B2为下面继续优化的目标，即，基于S形薄壁梁的截面尺寸与加强筋的几何尺寸对模型B2进行多目标优化设计，从而获得既满足轻量化要求，其抗撞性又明显优于原结构O的设计方案。

图5 模型A1与B2的变形图Fig.5 Deformation of the models A1 and B2

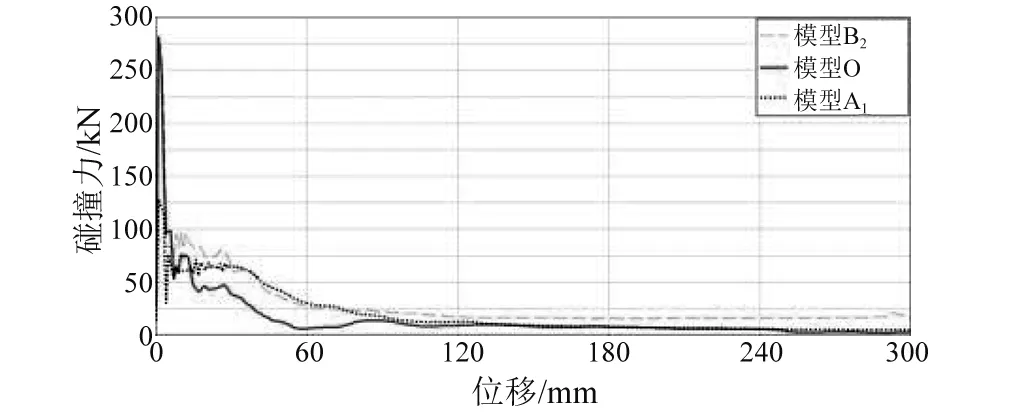
图6 3种模型的碰撞力-位移曲线对比Fig.6 Comparison of three force-displacement curves

3 基于抗撞性的方形截面S形薄壁梁的多目标优化

3.1 方形截面S形薄壁梁多目标优化建模

本部分优化的目的是，在保证模型B2优化后的总质量不大于原模型O的情况下，其抗撞能力明显优于原S形薄壁梁结构。因此本文以质量M(x)为约束，结合结构整体尺寸限制；取S型薄壁梁壁厚t1、 加强筋板厚t2与加强筋板长度l为设计变量； 以提高吸能量Ein和降低峰值碰撞力Fmax为优化目标，建立了不等式约束两目标优化问题的数学模型

(1)

式中：E(x)为碰撞过程中结构的吸能量；F(x)为峰值碰撞力；x为由3个设计变量组成的矢量；D={li≤xi≤ui,i=1,2,3}为设计域，li为设计变量xi的最小值，ui为其最大值； 约束条件M(x)≤Mmax表示结构总质量不能超过原结构模型O的总质量，Mmax=6.67 kg。根据强度和轻量化要求，设置ti∈[1.6,2.2]mm，i=1.2；l∈[380,420] mm。

3.2 代理模型的建立

首先采用正交试验设计[12]，以截面壁厚t1、加强筋板厚度t2及长度l为设计参数，共设置16组试验，通过Ls-dyna软件求解相应的吸能量Ein、峰值碰撞力Fmax和质量Mt； 然后采用多项式响应面法分别建立Ein与Fmax为优化目标函数，Mt为约束函数的代理模型如式(2)～式(4)所示

(2)

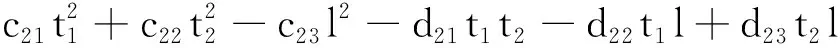
(3)

Mt≈M′(x)=a3+b31t1-b32t2+b33l

(4)

(5)

(6)

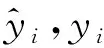
3.3 基于NSWFA算法的多目标优化设计

本文选取牛顿加权和弗里希法(Newton’s Weighted Sum Frisch Algorithm,NSWFA)[14]求解问题式(1)。为执行NSWFA算法，首先将目标函数式(2)、式(3)做归一化预处理，原问题转化为问题式(7)； 其中Emax和Fa分别为16组试验中吸能量Ein的最大值与碰撞力Fmax的平均值。

(7)

运用NSWFA算法求解问题式(7)：

(1) 加权和法对问题式(7)中目标函数等效标量化处理得和函数Fλ(x)， 即

Fλ(x)=λ1F1(x)+λ2F2(x)

(8)

式中： 权因子λ1,λ2>0， 且λ1+λ2=1。

(2) 利用Frisch内点罚函数法处理约束条件，建立罚函数项

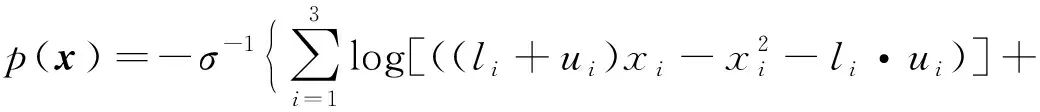
(9)

则问题式(7)等效转化为无约束单目标优化问题式(10)

Gλ(x)=Fλ(x)+p(x)

(10)

(3) 采用牛顿法快速获得问题式(10)的帕累托(Pareto)最优解集及其前端。

3.4 优化结果分析

根据“3.3”节获得的Pareto最优解集及其前端，依据S形薄壁梁抗撞能力的主要评价指标，选取一组最优参数对S形薄壁梁结构进行优化设计，建立有限元模型B4。仿真结果对比模型O与模型B2的性能指标，如表3所示。

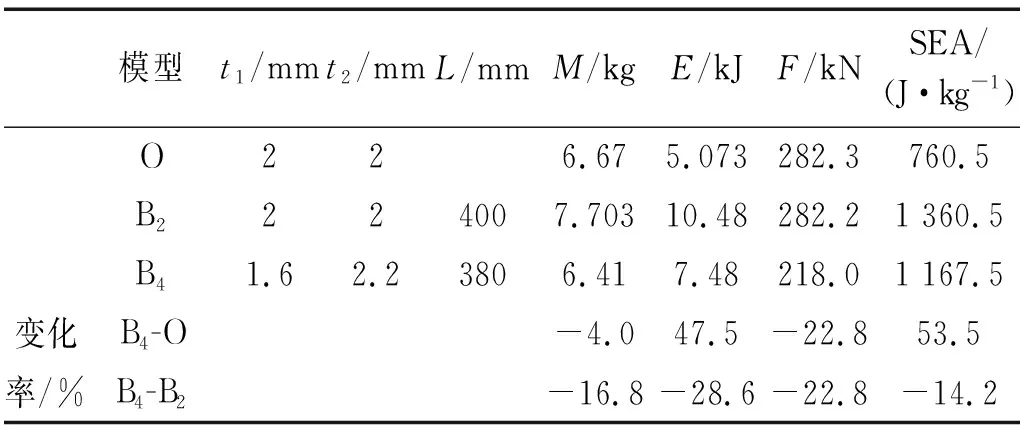
表3 S形薄壁梁结构优化前后性能参数对比

由表3可见，优化后的结构相对于模型B2，虽然吸能量Ein降低28.6%， 但是峰值碰撞力Fmax也降低了22.8%且总质量减少16.8%； 此外，相比原结构模型O，模型B4的Ein与SEA分别提高了47.5%与53.5%， 且Fmax与Mt分别降低22.8%与4.0%。综上可得，通过对模型B2进行多目标优化设计，得到了抗撞性较好且满足轻量化要求的S形前纵梁薄壁结构，即模型B4。

模型B4的碰撞力-位移仿真曲线与理论推导曲线对比，如图7所示。由图7可知，两条曲线吻合较好，与文献[15]结论一致，说明引入加强筋设计不影响原S形薄壁梁结构的截面力与其位移的数学关系且仿真结果与理论推导一致，同时验证了本文模型B4在正面碰撞过程中为有效变形。

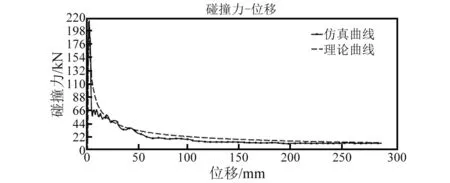
图7 碰撞力-位移曲线对比Fig.7 Comparison of force-displacement curves

3.5 基于加强筋板材料的薄壁梁轻量化设计

在保证S形薄壁梁结构的整体刚度和抗撞能力不降低的情况下，期待质量越小越好，从而提高单位重量的吸能能力。为此，本文在模型B4的基础上，把钢制加强筋板更换为质量更小的镁铝合金材料，建立有限元模型B5。对比原模型O与模型B4，各性能指标，如表4所示。

表4 3种不同模型的性能指标对比

由表4可知，相对于模型B4，模型B5的总质量Mt减少了11.1%； 峰值碰撞力Fmax降低了1.1%； SEA提高了5.18%。此外，与原模型O相比，Mt减少14.5%；Fmax降低23.6%； SEA提高61.5%。综合考虑抗撞性与轻量化要求，在模型B4的基础上将加强筋板材料更换为镁铝合金得到的S形薄壁梁模型B5，更加符合设计要求。

4 结 论

(1) 把诱导槽与加强筋设计，合理引入到S形薄壁梁结构，建立了多种有限元模型。以峰值碰撞力Fmax、吸能量Ein与SEA作为结构抗撞能力的评价指标，分析仿真结果可知：基于诱导槽设计的3种结构中，在S形薄壁梁的前部添加一个诱导槽的模型A1最优；而基于加强筋设计的4种模型中，在薄壁梁中间弯曲部分添加加强筋的模型B2，优于其他3种模型。

(2) 为满足轻量化要求，以模型B2的结构尺寸为设计变量所进行的多目标优化设计，使得优化后的模型B4相对于原模型O的吸能量与比吸能分别提高47.5%与53.5%；峰值碰撞力降低22.8%且结构总质量减少4.0%。

(3) 模型B4的碰撞力-位移的仿真曲线与理论曲线吻合较好，与文献[15]的结论一致，验证了新结构B4的有效性。

(4) 在模型B4的基础上，将加强筋板的材料更换为镁铝合金，建立有限元模型B5。仿真结果显示：相对于原模型O，模型B5的总质量减少14.5%；碰撞力降低23.6%； SEA提高了61.5%。

本文获得的新S形薄壁梁结构，抗撞能力及质量都明显优于原始的结构。