三维水下无线传感器网络覆盖方法*

吴克启， 郑润高， 王忠思

(1.海军士官学校 信息技术系，安徽 蚌埠 233012； 2.海军士官学校 教保处，安徽 蚌埠 233012)

0 引 言

水下无线传感器网络(underwater wireless sensor networks，UWSNs)是当前国内外无线传感器网络(wireless sensor networks，WSNs)领域的前沿技术和研究热点[1,2]。

目前，大多数关于传感器网络覆盖问题的研究都是在二维平面上考虑的，基于二维和陆上环境的WSNs覆盖需将目标监测区域抽象成二维平面多边形，然后分析二维平面上的点覆盖、区域覆盖或栅栏覆盖[3～5]。但随着WSNs在不同应用场景、领域和需求的研究，如在矿井、山岭、水下、太空等三维(3D)的环境下，这种忽略高度的二维平面模型已经不再适用，必须要在三维环境中进行分析和建模，对空间进行拓展以构建三维模型。

本文针对UWSNs节点的覆盖问题提出了三维网络模型与最优部署模型有效提高了网络覆盖率。

1 三维网络模型与最优部署模型

1.1 三维网络模型

本文研究UWSNs的部署和覆盖问题，传感器节点采用水下固定锚节点，节点一旦被部署后不能水平移动，只能在垂直方向上任意沉降，监测区域为某海域水下一个长方体区域F(L×W×H)。节点感知模型为布尔模型，节点感知半径为Rs，通信半径为Rt。在初始阶段，有M个节点随机部署于监测区域二维水面，随后，这些节点会被锚固定在海底，节点所处深度由连接锚与节点间的缆绳长度所决定。节点在随机布放后能通过自身的定位系统获知自身坐标，并传送给中心节点。

1.2 三维覆盖最优部署模型

传感器节点的覆盖模型拓展到三维空间以球形表示，这种覆盖模型与三维空间内的球堆积问题一致。在最密堆积中，许多相同半径球并置，使其空间利用率达到最大。

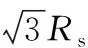
图1 面心立方格

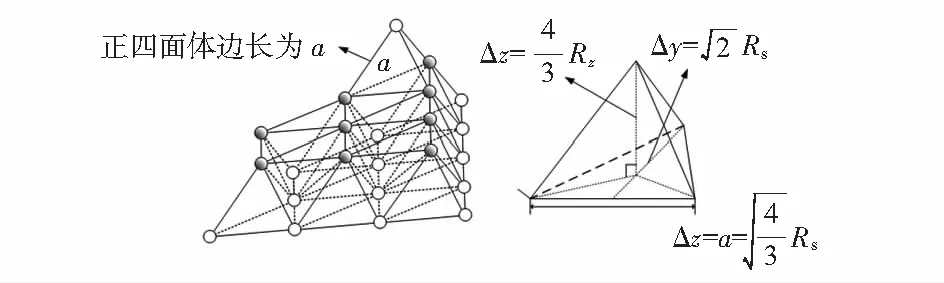
图2 三维覆盖最优部署结构

按照以上空间划分法，推导出节点数目计算公式为

(1)

式中N为实现完全覆盖时需要部署的最少节点个数;L，W，H分别为覆盖区域的长、宽、高;Rs为节点感知半径;[m]为不小于m的最小整数。

2 基于加权二分图完美匹配的节点选择与沉降

2.1 二分图完美匹配模型

本文所述加权二分图完美匹配指的是将水面大量随机部署节点(子集A)基于距离权值一对一的分配给区域内理想部署点(子集B)，从而实现“N项目”与“N目标”的最佳匹配。对该目标分配问题进行建模，现设子集A中随机节点个数为M，子集B中理想部署下实现完全覆盖所需最少节点数为N，则目标分配问题的模型可以描述为

(2)

满足以下条件

(3)

式中D=[dij]M×N为距离评价矩阵，dij为第j个随机节点距离第i个理想部署点的水平欧氏距离。因为锚节点在垂直方向的高度可以根据需要任意调节，因此,节点沉降后其垂直方向上的距离差Δz=0，在距离评价矩阵中只考虑随机部署节点与理想部署位置的水平欧氏距离。令X=[xij](M×N)为节点目标分配的解矩阵，当xij值为1时，表示随机部署节点i指派给理想部署位置j；否则，未指派。且条件限定于解矩阵的每行只能有1个1，每列只能有1个1，即1个理想图案位置只分配1个随机部署节点。

2.2 节点选择与沉降算法

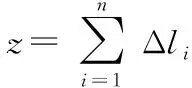
3 基于聚类算法的覆盖空洞检测和修复方法

3.1 覆盖空洞检测

经匈牙利算法进行节点指派和沉降后，由于沉降节点不可能正好在理想图案位置，总会存在一定的距离偏差，影响了整体的覆盖效果，会存在覆盖空洞。一般来说，随机节点个数M大于完全覆盖所需最少节点数N，即存在冗余节点。为提高网络覆盖率，考虑利用冗余节点进行覆盖空洞修复。对于覆盖空洞的检测，本文提出基于三维泰森图(3D-Voronoi)晶胞结构的覆盖空洞检测算法。

按照文献[10]对空间点集Voronoi图的海量构造及生成方法在MATLAB中绘制水下三维区域内由理想部署点形成的三维泰森图如图3所示，在空间内部，晶胞体呈现规则的正十二面体，处于区域边界的晶胞会被边界分割呈现新的形状。

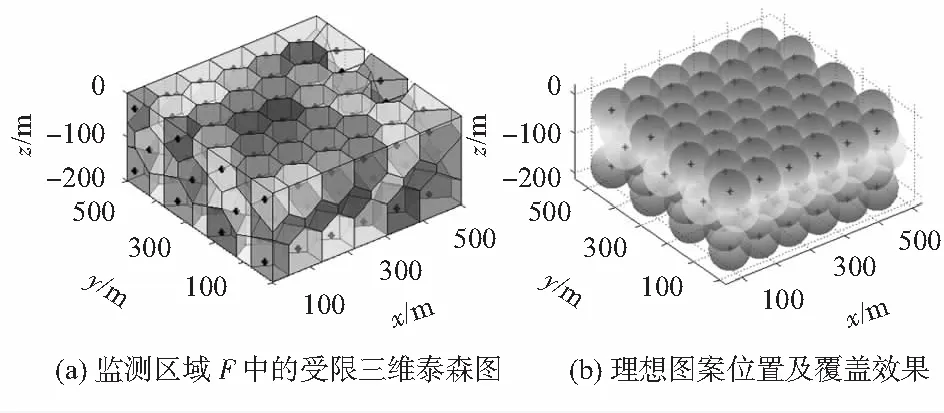
图3 部署节点的三维泰森图与覆盖效果

当节点分配指派算法执行后，由于指派节点水平方向上坐标的偏差导致出现了不规则的晶胞体形状，部分晶胞体顶点远离晶核以及其他节点，则会出现覆盖空洞。本文中覆盖空洞的检测基于三维泰森图晶胞体顶点完成，考察其顶点是否被任一部署节点覆盖，如果没有，则记为空洞点。图4给出了节点覆盖球、泰森晶胞和覆盖空洞点示意，图中球体为节点覆盖球，多面体为节点泰森晶胞体，晶胞上的顶点为覆盖空洞点。

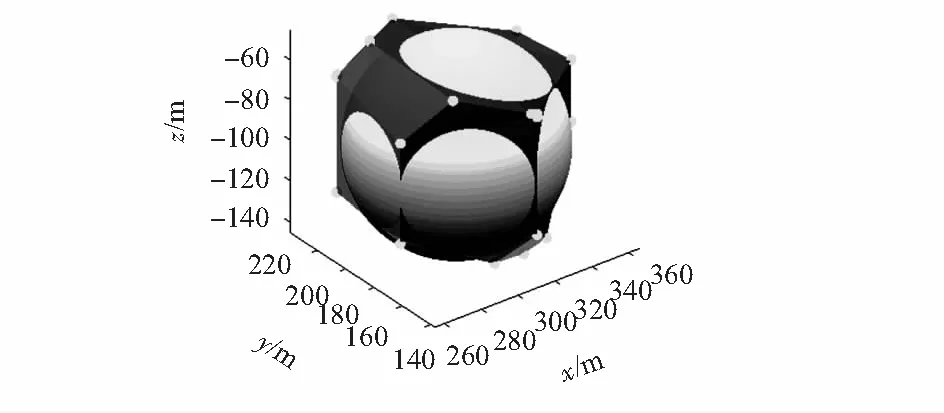
图4 节点覆盖球、泰森晶胞和覆盖空洞点示意

3.2 覆盖空洞修复

要实现对覆盖空洞的修复，需要将冗余节点沉降到覆盖空洞的位置。设节点指派后的冗余节点个数为M-N，令其等于K，则空洞点集H的聚类个数为K，聚类簇的质心位置为冗余节点的沉降位置。由于空洞点集的密集程度与该区域空洞点的大小之间存在一定的相关性，即一般来说空洞点密集的地方覆盖空洞也较大。鉴于以上特征，冗余节点可以指派到覆盖空洞点集的簇心位置，由于部署节点只能在初始部署位置的垂直方向沉降，因此,K个聚类簇的簇心只能是簇成员的z轴质心。使用K-means聚类算法得到K个沉降坐标的步骤如下：

1)随机赋予K个剩余节点一个z坐标，联合其水平坐标，作为K个初始簇心；

2)对所有的空洞点计算其到每个簇心的距离，并聚类到距离最近的簇心；

3)计算K个簇的z轴质心；

4)迭代步骤(2)～步骤(3)直至每个簇中点集成员不再发生变化，算法结束。

得到的K个簇的簇心位置即为冗余节点的沉降位置，冗余节点沉降后能够尽量多地覆盖空洞点，从而实现覆盖空洞的修复。

4 仿真实验与结果分析

4.1 仿真环境及参数设置

仿真实验基于MATLAB 7.10.0(2010a)实现。算法性能评估以网络覆盖率和连通度为主要指标。仿真数据采用20次以上实验计算所得的平均值，实验中所用参数为：网络覆盖区域F为500 m×500 m×200 m,随机部署节点数M为150～500,传感器感知半径Rs为50 m，传感器通信半径Rt为80～100 m，理想部署节点数N由式(1)计算。在仿真实验中，对比文献[11]算法(基于2D-voronoi的节点深度调节算法，记为Voronoi)。本文提出的基于二分图最佳指派的沉降算法记为BipGraph算法，指派后进行覆盖空洞修复的算法记为OptBipGraph算法。

4.2 实验结果与性能分析

图5给出了节点的三维部署，其中左图为3种算法的三维泰森图，右图为3种算法的节点三维覆盖效果，从图中部署节点的分布来看，本文提出的算法节点部署后分布更加均匀，节点空间覆盖效率更高。

图5 传感器节点三维部署

图6(a)给出了3种算法网络覆盖率性能(CovRatio)在不同部署节点数目(the number of nodes)下的变化情况。可以看出，3种算法覆盖率均随部署节点数目的增加而增大，其中Voronoi算法性能最差。但随着部署节点数目的增多，当M>380时，Voronoi算法性能优于BipGraph算法，这是因为BipGraph算法只部署了理想图案位置个数的节点，即只沉降部署了N个节点，部分冗余节点并未参与网络覆盖，故最终其覆盖率曲线趋于平缓。在几种算法中，本文提出的OptBipGraph算法性能最好，覆盖率相较于Voronoi算法提高达15 %。图6(b)、图6(c)比较了随机部署策略(Random)、Voronoi,OptBipGraph 3种算法的网络连通度(GaintTreRatio)性能。从图(b)可以看出，网络连通度随部署节点数目增加而增大，当节点数目大于200时，连通度均能达到95 %以上，当节点数目大于400时，连通度均能达到100 %。从图6(c)可以看出，网络连通度随节点通信半径的增加而增大，当节点通信、感知半径比Rt/Rs≥1.7时，网络连通度均能达到95 %以上。Rt/Rs≥2时，网络连通度均达到100 %。总体上，几种算法的网络连通度性能差异并不大，相比较而言，Voronoi算法在网络连通度性能方面略微优于OptBipGraph算法，而Random随机部署方法性能最差。

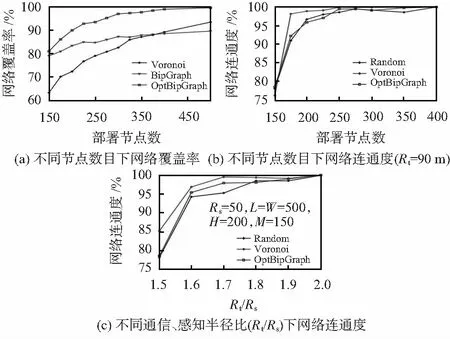
图6 CovRatio和GaintTreRatio性能比较

5 结 论

本文针对水下无线传感器网络节点的覆盖问题，在对覆盖区域进行最优化网格划分的基础上，得出三维空间无线传感器节点部署的理想坐标点，利用二分图最佳指派算法，将水面大量随机节点一对一的分配给理想部署点，并将冗余节点用于覆盖空洞的修复，采用基于三维泰森多面体晶胞结构的覆盖空洞检测算法和空洞点集聚类算法部署冗余节点，以优化水下无线传感器网络的覆盖。仿真结果表明:与已有的水下三维传感器网络部署算法相比，在保证网络连通度性能相当的情况下，本文提出的算法明显提升了传感器网络的覆盖率，性能提升达到15 %以上。