探寻求解通法 呈现最优解法*
——一道不规则四边形赛题的解法探究
2018-09-27
●
(沙坡头区宣和镇张洪学校,宁夏 中卫 755006)
1 试题呈现

( )
A.45° B.60° C.75° D.90°
(2017年全国初中数学邀请赛试题第4题)
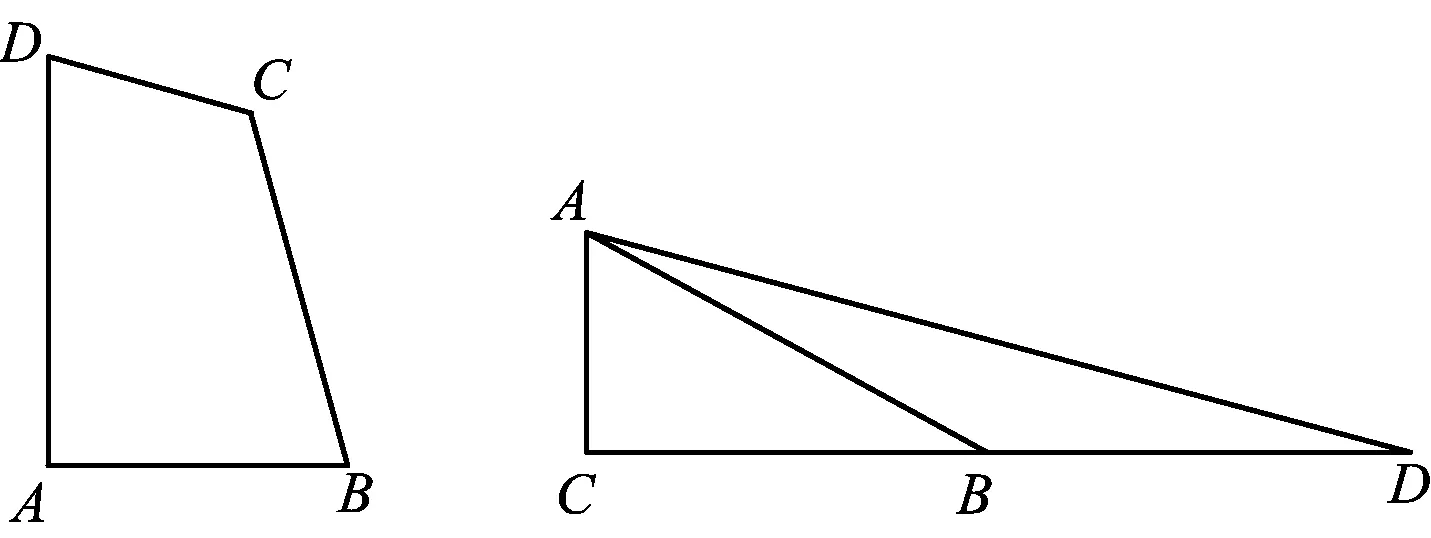
图1 图2
2 解法探究
为方便求解,先求15°和75°角的三角函数值.
如图2,在Rt△ACD中,∠C=90°,∠ABC=30°,AB=BD.令AC=m,则
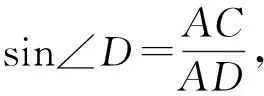

受文献[1]的启发,从图形特征出发,本题有以下两种求解思路.
思路1构造相似三角形求解.
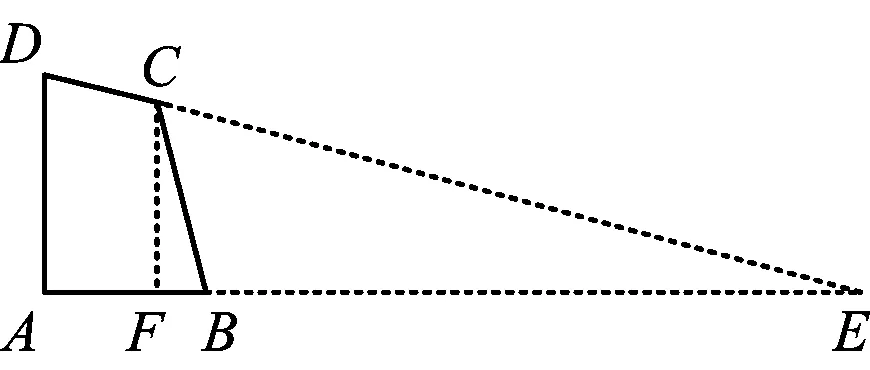
图3
解法1如图3,延长AB,交DC的延长线于点E,过点C作CF⊥AB,垂足为F.
由∠ABC=75°和∠BCD=120°,易知
∠E=∠BCF=15°,
求得

又因为∠AED=∠FEC=15°,所以
△CFE∽△DAE,
从而∠CDA=∠ECF=75°.故选C.

图4
解法2如图4,延长AB,交DC的延长线于点E,过点B作BF⊥DE,垂足为F.
由∠ABC=75°和
∠BCD=120°,易知
∠E=15°, ∠BCF=60°,
从而

又因为∠AED=∠FEB=15°,所以
△BEF∽△DEA,
从而∠CDA=∠EBF=75°.故选C.
点评以上两种解法均是通过构造直角三角形,利用直角三角形的边角关系求得相关线段的长,然后借助于相似三角形的判定和性质求得∠CDA的度数,不妨称这种构造相似三角形的方法为“相似三角形构造法”.这两种解法中,虽然构造的直角三角形不同,但直角三角形中均含有15°和75°角,因此求解相关线段长度的运算较为繁琐,运算量较大.将不规则的四边形转化为三角形,是解决不规则四边形问题的常用方法之一.通过计算可知,∠A=90°,因此本题采用“相似三角形构造法”可以成功解决.若在四边形ABCD中,∠A≠90°,则解法1和解法2对本题而言无能为力.由此可以看出,“相似三角形构造法”不是解决这类问题的通性通法,不具有“普适性”.
思路2构造直角三角形求解.
解法3如图5,联结AC,过点C作CE⊥AB,垂足为E,过点A作AF⊥CD,垂足为F.易知
从而
得
∠ACE=30°,
故
∠ACD=75°.
可知
于是
即
得∠CDA=75°.故选C.
点评解法3将四边形ABCD分割为4个直角三角形,然后利用直角三角形的边角关系求解.这种解法容易想到,但涉及到15°和75°角的三角函数,运算较为繁琐.

图5 图6
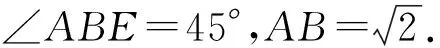
即
从而
AB=AE,
于是
∠AEB=∠ABE=45°.
在△CDE中,CD=CE=1,∠DCE=120°-90°=30°,得
∠CED=∠CDE=75°,
从而
∠CED+∠CEB+∠BEA=180°,
即点E在AD上,于是∠CDA=75°.故选C.
点评解法4通过构造Rt△BCE,将不规则四边形问题转化为两个新问题:一是判断△ABE的形状,这需要利用余弦定理求AE的长;二是判断点E的位置,这需要利用相关角之间的关系说明点A,E,D共线.对学生而言,解决这两个问题有一定的挑战性,况且构造这种非常特殊的直角三角形的方法不易想到,具有一定的难度.
受波利亚“怎样解题表”[2]及文献[3]的影响,笔者联想到这样一类几何计算问题:在网格图中求不规则格点多边形的面积.解决这类问题的常用方法有两种:一是将格点多边形置于某个矩形内,然后借助于直角三角形和矩形的面积求得不规则多边形的面积;二是将不规则四边形沿网格线分割成直角三角形和矩形,然后借助于直角三角形和矩形的面积求得不规则多边形的面积.受这种转化思想的启发,笔者尝试通过构造矩形或分割四边形解决本题.
思路3构造矩形求解.
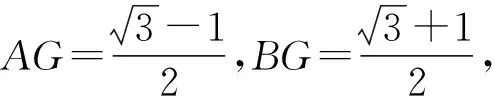
从而
于是
∠ADF=75°,
即
∠CDA=180°-∠ADF-∠CDE=75°.
故选C.
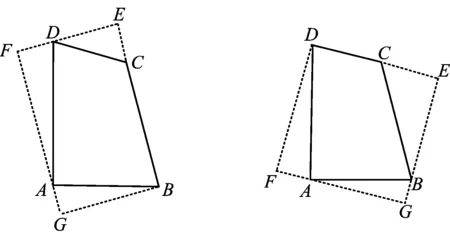
图7 图8
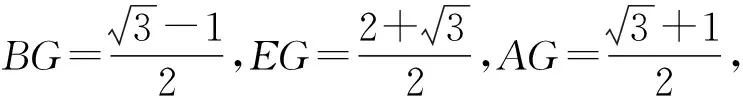
从而
于是
∠ADF=15°,
即
∠CDA=90°-∠ADF=75°.
故选C.
说明:四边形EDFG是正方形.
解法7如图9,过点C在四边形ABCD外作直线EH,使∠DCE=45°,过点B,D分别作直线EH的垂线,垂足分别为H,E,过点A作直线EH的平行线,交DE于点F,交BH于点G,则四边形EFGH是矩形,易知∠BCH=15°,∠CBH=75°,∠ABG=30°,∠BAG=60°,∠CDE=45°.又
由矩形的性质易知
从而
于是
∠ADF=60°,
即
∠CDA=180°-60°-45°=75°.
故选C.

图9 图10
解法8如图10,过点C在四边形ABCD外作直线EH,使∠BCH=45°,过点B,D分别作直线EH的垂线,垂足分别为H,E,过点A作直线EH的平行线,交DE于点F,交BH于点G,则四边形EFGH是矩形,易知∠DCE=15°,∠CDE=75°,∠CBH=45°,∠ABG=60°,∠BAG=30°.又
由矩形的性质易知
从而
于是
∠ADF=30°,
即
∠CDA=180°-30°-75°=75°.
故选C.

图11

从而
tan ∠ADF=1,
于是
∠ADF=45°,
即
∠CDA=180°-45°-60°=75°.
故选C.
点评解法5~9均是通过构造矩形解决问题.这些解法的基本特点是将不规则的四边形ABCD置于某个矩形之内,然后利用矩形及直角三角形的性质求解,不妨称这种方法为“矩形构造法”.从求解过程可以看出,这些解法中构造出了含有15°,30°,45°,60°,75°等特殊角的直角三角形,然后利用三角函数求得相关线段的长,这是学生非常熟悉的解决问题的基本方法.若涉及到15°和75°角的三角函数值,运算过程较为繁琐,对学生而言有一定的难度;若只涉及30°,45°,60°等特殊角的三角函数值,则运算量较小.对于解法9而言,求解过程中只涉及30°,45°,60°等特殊角的三角函数值,求解过程简洁明了,是“矩形构造法”中最为精妙的解法.因此,“矩形构造法”是解决不规则四边形问题的一种通法,具有“普适性”.
思路4分割不规则四边形为直角三角形和矩形.
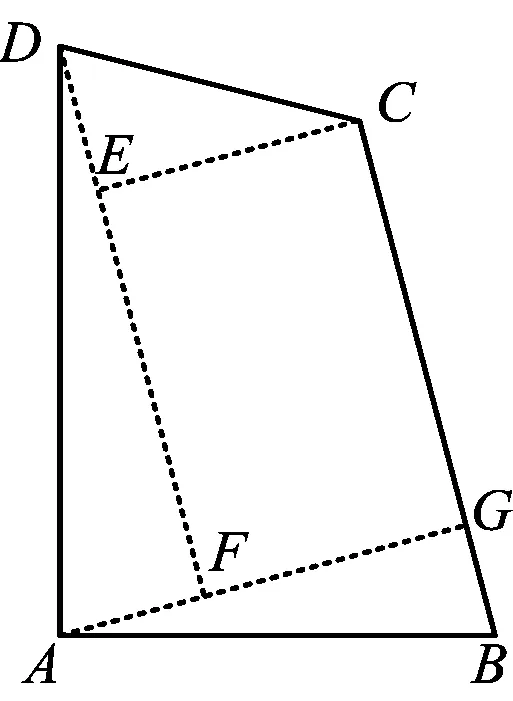
图12

从而
于是
得
∠ADF=15°, ∠CDA=15°+60°=75°.
故选C.

从而
于是
即
∠CDA=75°.
故选C.
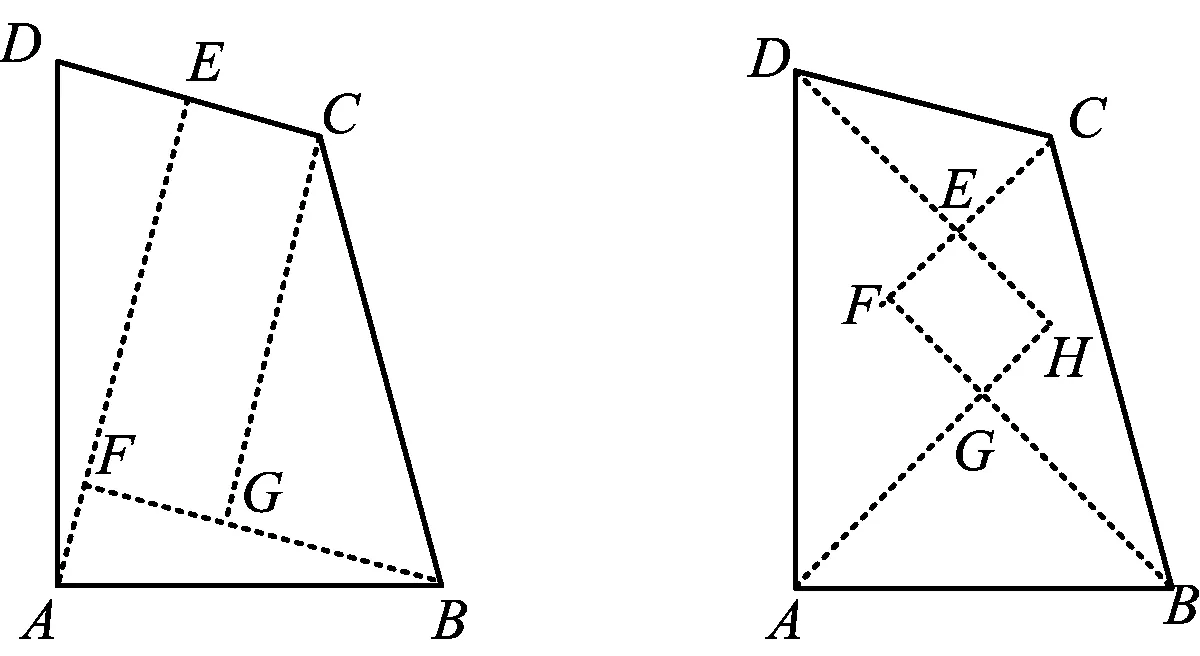
图13 图14
解法12(最优解法2)如图14,作∠C的平分线CF,分别过点B,D作CF的垂线,垂足分别为F,E,过点A作BF的垂线,垂足为G,AG交DE于点H,则四边形EFGH是矩形.易知∠DCE=60°,∠CDE=30°,∠BCF=60°,∠CBF=30°,∠ABG=45°,∠BAG=45°.又
得
从而
于是
tan ∠ADH=1,
即
∠ADH=45°, ∠CDA=45°+30°=75°.
故选C.
点评解法10~12均是将不规则四边形ABCD分割为直角三角形和矩形,借助于直角三角形和矩形的性质解决问题.从求解过程可以看出,这些解法均是从∠BCD入手,将其分为两个特殊角,然后构造直角三角形.以上解法中构造出了含有15°,30°,45°,60°,75°等特殊角的直角三角形,然后利用三角函数求得了相关线段的长.对于解法12而言,求解过程中只涉及30°,45°,60°等特殊角的三角函数值,求解过程简洁明了,是这类求解方法中最为精妙的解法.由此可以看出,将不规则四边形分割为直角三角形和矩形也是解决不规则四边形问题的一种通法,具有“普适性”.
3 类题链接
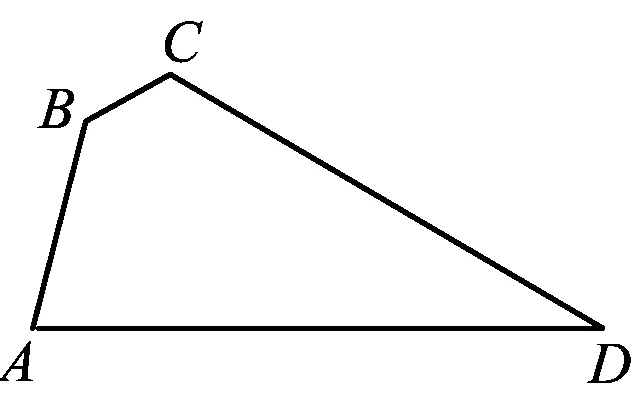
图15
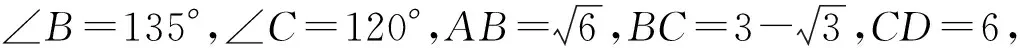
( )

(2013年全国初中数学联赛初三试题第4题)
请有兴趣的读者自行解答,此处从略.
4 结束语
数学学习离不开解题,解题是数学教学中极具创造性的工作.数学解题是一个培养数学思维能力的过程,是一种尝试、探索、联想、发现的过程.在解决某些几何问题的过程中,最先想到的解法可能是满足题目本身特征的特殊解法,不具有“普适性”,不是解决这类问题的通性通法.若联想到数学学习中较为相似的几何问题,则可能会找到通性通法的突破点.回望本题的求解历程,笔者利用几何画板作图时,就已发现了∠CDA=75°,∠A=90°,但要严格证明,并非易事.笔者想到了构造直角三角形,然后说明构造的直角三角形与所在的三角形相似,从而说明∠A=90°,∠CDA=75°,这种特殊的解法对于其他同类问题无能为力.在多次尝试后,仍然不得其法.于是笔者联想到了网格中求解不规则四边形的面积问题,点燃了思维的火花,得到了求解本题的通性通法,并在诸多通法中呈现了两种最优解法.
因此,在数学学习中,要关注求解同一类问题的通性通法,形成解决同一类问题的基本套路,这对提高学生数学解题能力有一定的促进作用.
