靶板厚度对卵形弹丸垂直贯穿中等厚度 混凝土靶的影响*

刘志林,王晓鸣,李文彬,姚文进,宋梅利

(南京理工大学智能弹药技术国防重点学科实验室,江苏 南京 210094)

与深侵彻研究类似，弹丸贯穿有限厚度靶的研究对先进钻地武器的研究和防护设计工程具有重要的意义。弹丸贯穿靶体是一个复杂的过程，当弹丸贯穿混凝土靶后，靶板破坏严重，靶板背面产生大面积崩落的混凝土碎块，从而对掩体内的人员和设备造成严重的次生破坏。现有的ACE、NDRC等经验公式[1]都可以对弹丸侵彻和贯穿混凝土介质的侵彻深度和弹道极限进行较为有效的工程预测，但由于使用范围的限制，很难得到更为广泛的应用。近年来很多方法，包括解析模型和数值分析模型，都可以对各种弹体贯穿薄靶进行预测，Hanchak等[2]、Yankelevsky[3]、Dancygier[4]、葛涛等[5]都对弹丸贯穿混凝土问题做了研究。相对于半无限靶的深侵彻研究，有限靶的贯穿问题主要涉及到靶背效应问题，由于混凝土的拉伸强度远远小于其压缩强度，弹丸侵彻过程中会形成压缩波并向弹丸前进方向传播，当压缩波传播到靶体背面的自由面时，压缩波反射之后变为拉伸波。当应力超过混凝土的抗拉强度时，混凝土会发生断裂，并形成靶背的崩落现象。混凝土介质材料的动态力学性能主要由其状态方程、强度方程和失效准则三个方程表征。侵彻问题中的混凝土本构最常用的是HJC 模型[6]，HJC 模型主要综合考虑了大应变、高应变率、高压效应等因素，较为适合Lagrangian和Euler网格下的计算模拟，其等效屈服强度与静水压力、应变率以及损伤的函数，结合三阶段的状态方程，其模拟弹丸深侵彻问题十分适用，模拟结果精确。但此模型没有考虑第三不变应力张量的影响，且其不能很好地模拟开坑、剥落等现象。

为了研究卵形弹丸的贯穿中等厚度混凝土靶体的靶体厚度对剩余速度的影响规律，本文中利用火炮发射平台，采用次口径发射技术，开展了60 mm直径弹丸贯穿不同厚度混凝土靶的实验研究。结合无网格方法、考虑3个极限面的RHT混凝土本构和多孔介质p-α状态方程，对弹丸贯穿薄靶和厚靶的贯穿效应进行了模拟，分析了弹丸贯穿过程以及其损伤演化，获得了不同厚度靶对贯穿的影响规律。

1 实 验

1.1 实验方案

图1 实验场地布置图Fig.1 Layout of experimental site

图2 弹体装配实物Fig.2 Photograph of assembled projectile

1.2 实验结果

弹丸贯穿混凝土的实验中，撞击速度和贯穿余速是实验中需要测量的重要参数。实验中采用高速摄像机用于弹丸入靶姿态捕捉和入靶前撞击速度的测量，以及弹丸穿透靶板后弹丸出靶姿态和出靶速度的测量。

表1 实验结果Table 1 Experimental results

实验结果如表1所示，结果显示弹丸的撞击速度与设计速度相当，除3号射击外其余5发射击实验的弹丸都贯穿了混凝土靶体，被贯穿后靶体的破坏状态如图3～4所示。

图3 1号工况下靶体破坏图Fig.3 Failure of concrete target after impact under case 1

图4 3号工况下靶体破坏图Fig.4 Failure of concrete target after impact under case 3

从图3～4中可以看出靶体呈整体破坏，且多处径向扩展的宏观裂纹发展到靶体侧面，迎弹面有漏斗形开坑区。靶背有大面的崩落区，崩落区的面积与深度明显大于迎弹面的开坑面积和深度。其他4 种贯穿射击后的靶体破坏与1号射击工况类似。3号射击工况与其他5发射击结果不同，实验后的弹丸停留在靶体背面，靶体的背面有很大崩落区，弹丸的头部裸露在靶体外，如图4(b)所示。靶体的迎弹面和其他靶体的现象类似，有类似于圆形的开坑区。3号射击工况结果显示，此发射击条件下靶板的厚度非常接近此侵彻速度下的靶板的震塌破坏临界厚度。

2 数值模型

2.1 侵彻模型

图5为本文数值模拟采用的侵彻模型，模型尺寸与实验尺寸比为1∶1，弹丸采用Lagrangian网格，见图6；靶板采用SPH粒子单元，粒子间距为2.5 mm，计算模型采用轴对称模型。

图5 侵彻模型Fig.5 Penetration model

图6 弹体网格划分Fig.6 Mesh division of projectile calculation model

2.2 混凝土本构及参数

选用RHT模型[7]作为贯穿模拟的混凝土介质本构，RHT模型最早是由Riedel等提出的混凝土本构模型，其是由3个极限面(弹性极限面、失效面、剩余强度面)来描述混凝土的动态力学性能。该模型考虑了第三不变应力偏张量的影响，在预测混凝土深侵彻方面结果理想，且在描述侵彻过程中的混凝土损伤变化有一定的优势。本文中结合SPH方法和RHT混凝土本构以及多孔介质p-α状态方程，模拟弹丸侵彻贯穿混凝土过程，研究弹丸开坑和崩落现象发生过程，同样为研究贯穿工程模型提供数据支持，混凝土材料的具体参数可参考文献[8-10]。

3 结果与讨论

3.1 贯穿过程分析

数值模拟以复现贯穿实验为目的，主要是研究弹丸在同一速度下撞击不同厚度靶体后的弹丸余速的规律。计算中的靶板厚度在10～30D范围内，速度有650 m/s低速和1 100 m/s高速。此工况下，弹丸的贯穿过程分为3个阶段穿透，分别为开坑段、隧道段和出靶段。

图7显示了弹丸以650 m/s速度撞击0.8 m厚混凝土靶板的数值计算结果的损伤演化过程图，损伤云图中红色代表材料完全损伤，蓝色代表未损伤，在RHT模型中的损伤δ是材料的塑性应变增量的积累与材料失效塑性应变的比值，其值在0到1范围内。取t=2.6 ms时刻的靶板损伤为最终损伤状态，在t=2.6 ms时刻，靶板的开坑区、隧道区和冲切区都非常明显。2号射击工况的弹丸余速比1号射击工况的低，弹丸与冲切区混凝土的相互作用持续的时间较长，冲切区的混凝土冲出的速度较1号射击工况的小，1号射击工况测得的弹丸余速为308 m/s，数值计算弹丸余速结果为379 m/s，弹丸在冲切段与混凝土的响应主要以局部响应为主，弹丸贯穿了损伤后的冲切区的混凝土，弹丸头部会穿透整个靶面，且继续向外飞行，与混凝土完全分离。冲切区混凝土在与弹丸分离后向外飞散，且离隧道区近的碎片速度较大，这一结果与实验结果完全一致。在靶背影响区域内的弹丸消耗的能量情况见表2，结果显示了弹丸余速越小，弹丸在靶背影响区域消耗的动能越大，表明弹丸余速越小，与混凝土作用时间越长，损失的能量越大。

图7 靶被贯穿过程损伤云图Fig.7 Damage contour of target during penetration process

实验编号H/D进入靶背影响区的速度/(m·s-1)弹丸消耗的能量/J110.04601.4×105213.34342.8×105316.74283.8×105423.36302.0×105526.75412.2×105630.05023.2×105

图8 靶被贯穿破坏的数值模拟结果 Fig.8 Simulation results of concrete target damage

在6发射击的贯穿过程中，除3号射击工况外，其余5发贯穿的余速都相对比较高(大于200 m/s)，其贯穿过程与1号射击情况工况类似。将3号发射工况的靶背最终破坏情况的数值模拟结果(图8)与实验结果(图9)进行对比发现，数值模拟结果与实验一致，此工况下的弹丸停留在靶体内部，且靶后有大质量块混凝土被冲切出靶体。弹丸的侵彻深度为74.2 cm(实验值为79.5 cm)，冲切出的靶体的飞溅速度在6 m/s。3号射击工况的弹丸的余速为零，实验中3号射击工况高速录像靶后破坏过程见图9(b)，靶后有大体积混凝土块向外冲出，且混凝土块整体以一速度向外飞出(混凝土块的飞出速度约为17 m/s)，可以判断，混凝土块发生冲切破坏。图9(a)显示了3号射击工况的靶板背面的破坏形态，中间发光物体的为停留在靶体中的弹丸，弹丸头部裸露在空气中，弹身埋没在靶体中。结果表明在弹丸冲击厚靶时，当弹丸在靶背影响区时弹丸速度很小时，冲出靶体的混凝土块与弹丸的响应以整体响应为主。

图9 靶被贯穿破坏的实验结果Fig.9 Experimental results of concrete target damage

3.2 过载分析

图10～11所示分别为在实验条件下的弹丸的速度和过载变化历程数值模拟结果，6条曲线分别代表了实验的6发射击工况。数值模拟中弹丸的撞击速度分为2种，为650和1 100 m/s，靶板厚度有6种，分别为0.6、0.8、1.0、1.4、1.6 和1.8 m。速度变化曲线显示，同一撞击速度下，随着靶板厚度的增加，弹丸的余速呈下降趋势；靶板厚度继续增加时，余速逐渐趋向于零，即弹丸没有贯穿靶板。相同撞击速度撞击不同厚度靶板的速度变化曲线图中，弹丸在撞击靶板后的速度曲线基本重合，在弹丸接近靶板靶背的自由面时，速度变化趋于平缓，直至弹丸贯穿整个靶板，速度趋于恒定值，也就是弹丸的贯穿余速，结果表明计算值与实验值吻合较好。

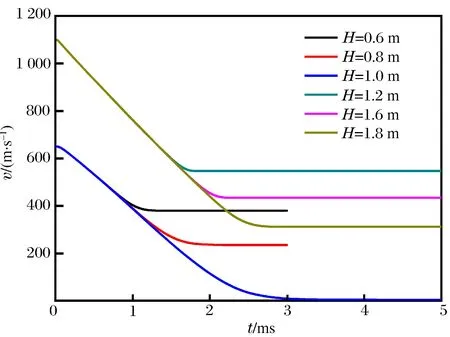
图10 弹丸速度时程曲线 Fig.10 Velocity-time curve of projectile

图11 弹丸过载时程曲线Fig.11 Acceleration-time curve of projectile

图12所示为弹丸撞击不同厚度靶的过载随时间的变化，弹丸撞击靶板后弹丸过载陡然上升直至稳定侵彻阶段，稳定侵彻阶段弹丸过载趋于恒定值，650 m/s速度下弹丸稳定侵彻的过载接近30 000g，1 100 m/s速度下约为35 000g。Rosenberg等[11]和Chen等[12]在对混凝土的常阻力假设的适用的初始撞击速度阈值达到1 200 m/s，本文的数值计算结果也就印证了这一结果。在弹丸继续侵彻，并接近靶背自由面时，弹丸的过载开始降低，并缓慢将至零，表明弹丸停止运动，或是弹丸完全贯穿混凝土靶。图12(a)为弹丸贯穿0.6 m 厚靶的弹丸过载随弹丸位移的曲线图，过载可以分为3个阶段：开坑阶段、隧道阶段(稳定侵彻阶段)和靶背自由面影响阶段。侵彻实验中，弹丸的开坑深度的散布较大，Forrestal等[13]建议开坑区的深度为2D，数值模拟结果显示，弹丸从开坑阶段进入稳定侵彻阶段的过渡区域也在深度2D处附近，本文取2D作为开坑阶段与稳定侵彻阶段的分界线；稳定侵彻阶段的弹丸过载接近为恒定值，稳定侵彻阶段结束的分界线由靶背自由面的影响区域决定，数值模拟中0.6 m的靶板的贯穿的自由面影响区域约在3.1D。自由面影响区域内，弹丸的过载逐渐降低直至为零。特别的，当弹丸头部运动至靶体背面的自由面时(Z=10D)，弹丸的过载还并未降至零，表明被弹丸冲出混凝土靶体的混凝土介质对弹丸还会有作用力。这3个分界时刻的损伤云图见图13，从损伤云图中可以发现，弹丸在开坑段以及稳定侵彻的过程中，离靶背3.1D厚度的区域内损伤积累相对于其他区域较为严重，当弹丸行至此区域时，弹丸过载稳步降低直至为零。

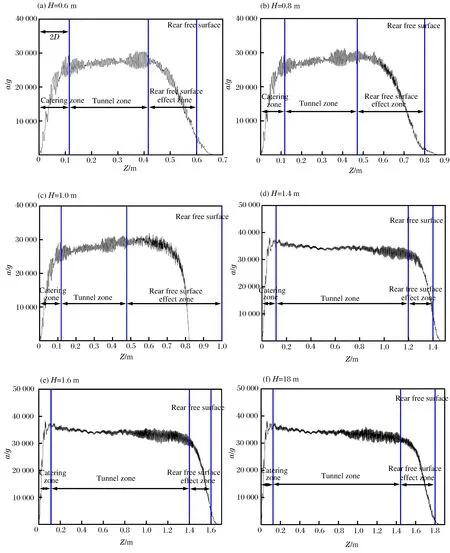
图12 弹丸过载与位移关系Fig.12 Relation between acceleration and displacement

厚度为0.8 m靶被贯穿的3个阶段与厚度为0.6 m靶被贯穿的过程类似，但靶背影响区域较厚度为0.6 m的靶有一定的增加(约5.6D)，弹丸贯穿厚度为1.4、1.6、和1.8 m靶的过载随位移的变化图见图12(d)～(f)，高速贯穿的过载曲线与低速相比，弹丸的开坑区域的厚度相对减小，表明弹丸更快的进入稳定侵彻阶段，但其减小的幅值有限，因开坑段不是本文研究的重点，本文中还是取2D作为开坑区的深度。随着靶板厚度的增加，隧道区域的厚度逐渐增加，靶背影响区的厚度也逐渐增加，弹丸的余速逐渐减小，隧道区的长度与靶背影响区的长度的数值模拟结果见表3。

图13 3个分界时刻的损伤云图Fig.13 Damage contour of different stages in penetration process at three instants of time

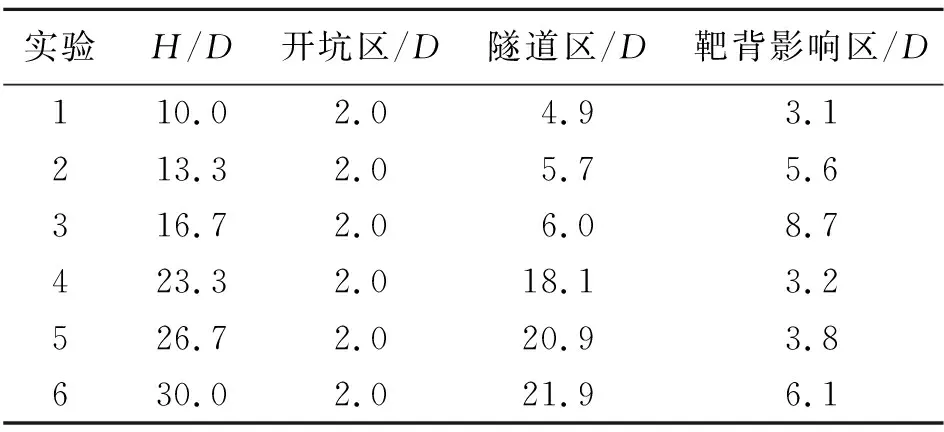
实验H/D开坑区/D隧道区/D靶背影响区/D110.02.04.93.1213.32.05.75.6316.72.06.08.7423.32.018.13.2526.72.020.93.8630.02.021.96.1

4 结 论

开展 60mm直径弹丸的贯穿中等厚度混凝土介质靶实验，靶体厚度在10～30D范围内，撞击速度为650和1 100 m/s，得到弹丸以相同速度撞击不同厚度混凝土介质靶体的弹丸余速变化规律。结合SPH无网格方法以及RHT混凝土本构以及考虑多孔特性的p-α状态方程，对实验工况进行的数值模拟，对实验结果和数值模拟结果进行分析总结，得出以下结论：

(1)采用的SPH无网格法结合RHT混凝土本构和考虑多孔特性的p-α状态方程方法，可以很好地模拟靶板的开坑与崩落失效响应，在弹丸贯穿混凝土介质问题的研究中取得较好的结果。

(2)贯穿实验表明：弹丸的剩余速度随着混凝土靶体厚度的增加而降低；隧道区和靶背影响区的厚度随着靶体整体厚度的增加而增加。

(3)数值模拟结果表明：在弹丸出靶速度低于阈值时，混凝土靶背发生冲塞现象；弹丸余速较大时，弹丸出靶时与冲切区的混凝土继续作用，弹丸在此过程中的过载稳步下降直至弹丸头部穿透靶板，过载降为零。