碎片云SPH方法数值模拟中的材料失效模型*

邸德宁，陈小伟

(1.中国工程物理研究院总体工程研究所，四川 绵阳 621999; 2.北京理工大学前沿交叉科学研究院，北京 100081; 3.北京理工大学爆炸科学与技术国家重点实验室，北京 100081)

光滑粒子流体动力学法(smoothed particle hydrodynamics, SPH)是一种Lagrange无网格粒子算法，超高速撞击中的强冲击波使材料表现出如流体一样的性质，伴随着材料大变形甚至破碎，传统网格方法难以求解，而基于流体动力学控制方程的SPH方法非常适用[1]。在SPH数值模拟前的处理中，必须设定材料模型，包括状态方程、强度模型和失效模型等。材料状态方程不可或缺，描述材料密度、压力和内能之间的关系；材料强度一般不可忽略，引入强度模型可计算材料偏应力张量和材料当前应变、应变率、温度等对屈服强度的影响。薄板超高速撞击中材料破碎形成碎片云的过程，被认为是稀疏波导致的拉应力超过材料断裂应力后材料不断层裂破坏的过程，而状态方程和强度模型均不能表征材料断裂方面的特征，因此需要考虑在计算中引入失效模型。

利用SPH方法对碎片云进行数值模拟，计算结果与实验吻合很好，但同时发现材料模型的选择对计算结果有影响。Groenenboom[2]发现SESAME状态方程在压力和径向速度方面稍小于多项式状态方程；张伟等[3]发现Tillotson和Puff状态方程相比于Shock状态方程，碎片云径向速度稍大，碎片云颗粒更细小且分散，而强度模型的选择对结果影响不大；Higashide等[4]发现不包含材料相变的状态方程计算得到的碎片最大，考虑材料液化和气化的热力学完全状态方程对相态分布计算较准确，其中考虑了亚稳态相态情况的状态方程计算结果最准确；李宝宝等[5]通过比较GRAY三相物态方程与Tillotson物态方程，也发现材料相变对碎片云外形尺寸影响较大。然而，SPH方法失效模型的选择尚无具体结论，有研究者认为SPH方法中不需要材料失效模型，另一些研究者则采用最大拉应力或Grady失效模型。另外，现有对材料模型方案的研究大多针对碎片云外形或运动状态，未能很好地讨论对碎片质量和数量分布的影响，以及影响程度与撞击工况的相关性，难以实际参考应用。

本文中，利用AUTODYN软件中的SPH模块，针对无失效模型、Grady失效模型和最大拉应力失效模型3种方案，考察失效模型对碎片云外形尺寸及速度、粒子点失效表现和碎片数量分布的影响，讨论失效模型的影响程度随撞击工况的变化，并比较Grady失效模型下不同失效阈值导致的碎片云差异。本文旨在补充SPH方法中材料模型的选择，对碎片云数值模拟特别是碎片分布进行深入分析。

1 碎片云几何表现的差异

1.1 计算模型设置

本文中所用算例共2部分，第1部分参照实验情况[6]，取直径为9.53 mm的球形弹丸，材料为2017-T4铝合金，采用Shock状态方程和Johnson-Cook强度模型；薄板材料为6061-T6铝合金，采用Shock状态方程和Steinberg-Guinan强度模型；弹丸正撞击薄板，表1中列出了共3种工况7个算例的薄板厚度、撞击速度及所采用的失效模型方案。

最大拉应力模型即材料拉应力超过设定的失效阈值后材料失效，本文中通过主应力失效实现，设定6061-T6铝合金的失效阈值为2.6 GPa[3]，2017-T4铝合金的失效阈值为2.5 GPa[6]，不考虑最大剪切力失效情况。

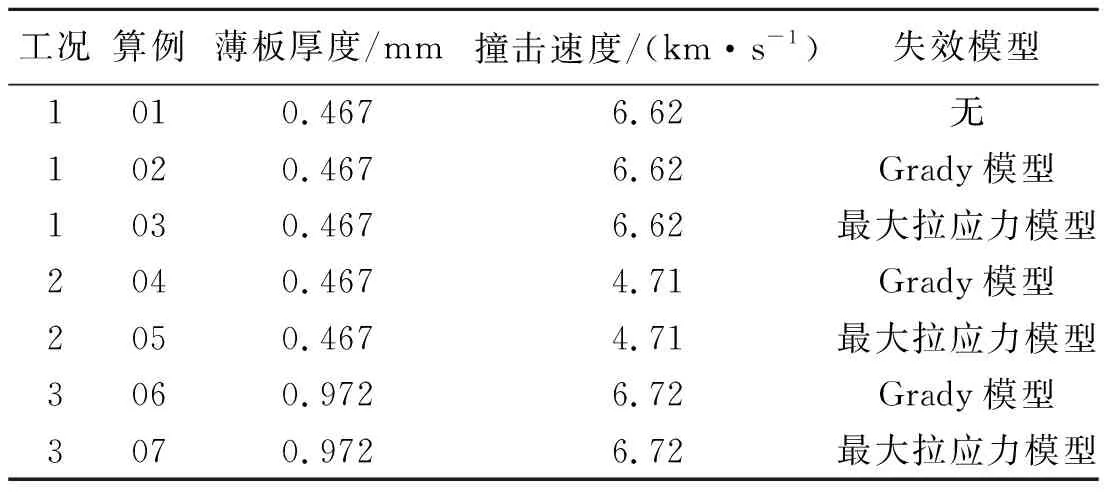
表1 各算例的设置Table 1 Settings of various cases

Grady失效模型同样基于主应力判断失效，即主应力超过失效阈值ps后材料失效，不同的是失效阈值ps非固定值，而由下式计算得到：

式中：ρ为材料密度，由材料连续性方程或核函数更新；Y为屈服强度，由材料强度模型根据材料当前应变、应变率和温度计算更新，变化幅度较大，对ps计算值影响严重；c0为材料体积声速，由材料体积模量和当前密度决定；εc为临界失效应变[7]，材料常数，铝合金材料一般取εc=0.15。可见，在不同区域、不同时刻，ps的取值均可能不同。

1.2 不同失效模型方案下碎片云几何表现的比较

为分析失效准则对碎片云计算结果的影响，设计了算例01～03作对比，算例01不引入失效模型，算例02采用Grady模型，算例03采用最大拉应力模型。另外，文中碎片云图像及分布统计均基于撞击后20 μs时的计算结果。

如图1对照所示，有、无失效模型对碎片云外形影响严重，特别是对弹丸碎片云部分；而Grady失效模型和最大拉应力失效模型的选择并无明显差别。测量碎片云整体尺寸，发现：算例01径向尺寸为算例02的81%，轴向尺寸为算例02的96%；算例03和算例02碎片云整体尺寸相差很小。

图1 算例01～03数值模拟结果Fig.1 Simulation results of cases 01-03

针对弹丸碎片云部分，图2为算例01～07弹丸碎片主体碎片识别结果放大图，其中碎片识别为只显示包含有未失效粒子的碎片。对比各图可见，算例01中粒子聚集紧密形成一个大碎片，包含了弹丸中94.8%的粒子点；算例02和算例03结果相近，碎片孤立并高度分散，但算例02中碎片更多，且最前端平整，更接近实验图像。算例01中碎片云尺寸明显偏小。分析算例02～07碎片云特征速度[6]发现，最大拉应力模型下碎片扩散程度不及Grady模型，即前端和径向速度偏小但后端速度偏大，不过两者相差不大，都和实验很接近。

综上，不引入失效准则的计算结果明显与实验不符，有失效模型的计算结果均与实验符合，但最大拉应力模型下碎片云的扩散程度稍弱于Grady模型下。

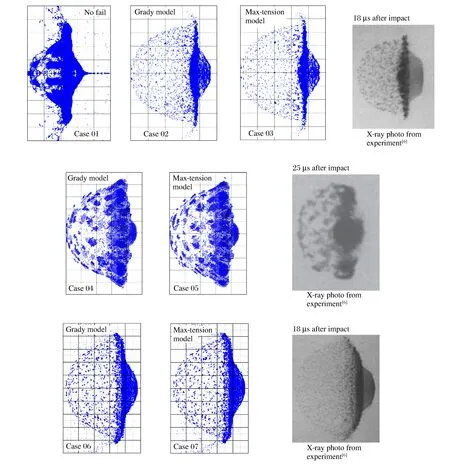
图2 算例01～07弹丸碎片云碎片识别结果与实验对照[6]Fig.2 Main parts of projectile fragments of cases 01-07 compared with experiments[6]

2 材料失效细观表现的差异

失效模型方案不同导致碎片云计算结果有差异，为分析其内在机理，在计算模型中设置测量点，提取粒子点压力-时间历程作对比分析。

2.1 有、无失效模型计算结果的差异

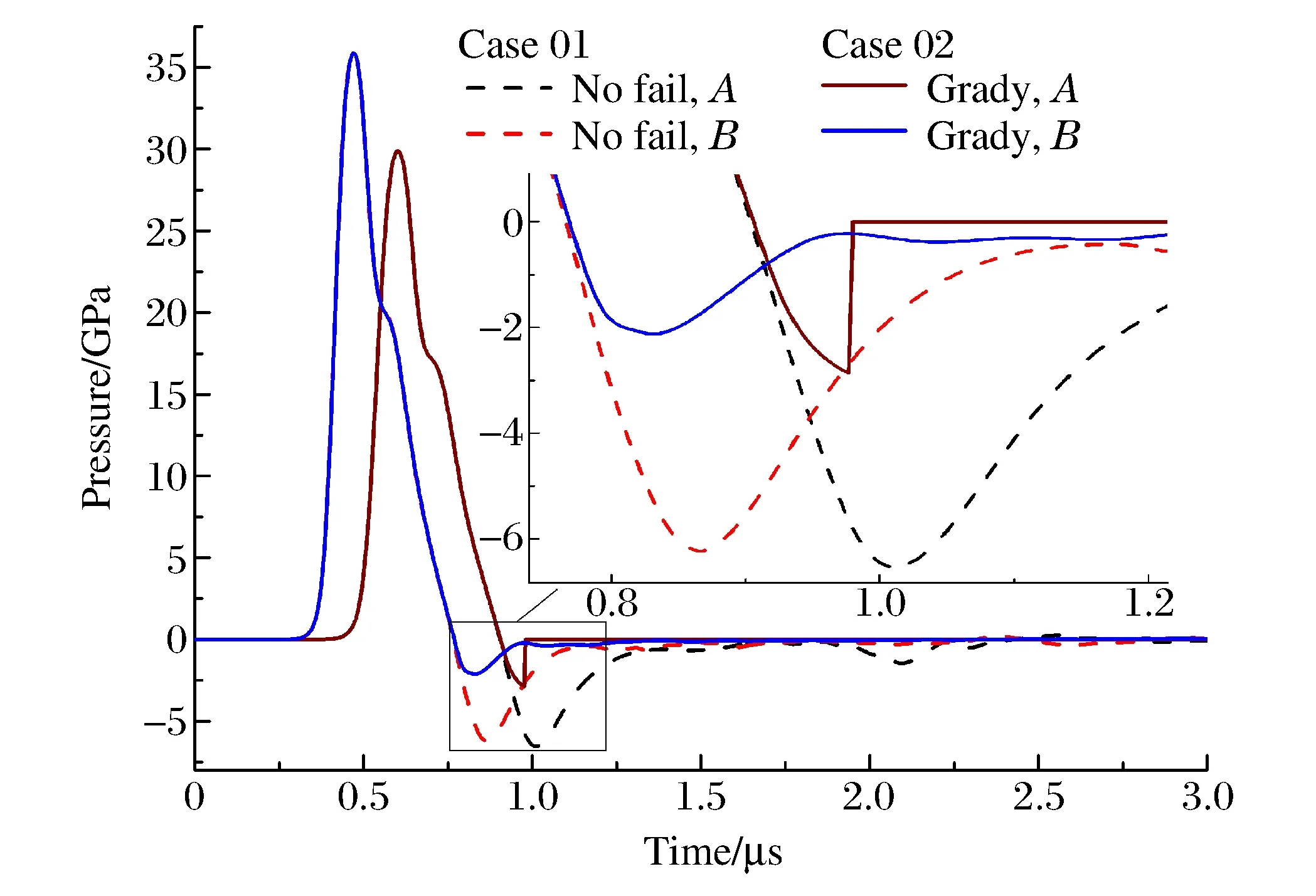
图3 测量点A、B压力时间历程Fig.3 Pressure-time curves of gauge points A and B

首先对比有、无失效模型的情况，在算例01和算例02中设置测量点A和B，图3绘制了测量点压力-时间历程。在冲击波作用段内同一测量点曲线完全重合，表明材料被冲击过程与失效模型无关。稀疏波到达一段时间后开始出现小的分歧，进入负压后曲线出现明显分歧。观察右上的放大图可见，算例01中测量点负压均超过6 GPa，并在达到峰值后圆滑回落；算例02中A点负压在到达2.86 GPa后突然跳到0 GPa并保持，B点负压在到达峰值2.12 GPa后圆滑回落，并在后期继续变化。上述差异正是由失效模型导致的，不引入失效模型时粒子点在强拉力下不会失效，从而完整地传递稀疏波，但这和工程材料拉伸断裂的实际表现明显不符；引入失效模型后，拉伸主应力超过失效阈值即会判为失效，粒子不再能承受拉应力或剪切力，如算例02中A点表现所示，负压跳变为0 GPa。

考虑失效模型对碎片云宏观表现的影响，当粒子点失效后不再承受拉应力，效果即为断裂点，会阻碍稀疏波的传播，从而导致断裂点两侧粒子运动状态差异较大，碎片高度分散。大量失效粒子会构成断裂面，一个孤立碎片的表面即为失效粒子组成的断裂面，碎片内部粒子表现如同算例02中B点，应力波在碎片内部振荡导致其压力值不为零。反之，不引入失效模型，则不会出现断裂点，通过SPH算法核函数近似，近邻粒子之间无障碍地相互影响，导致粒子点速度矢量比较接近从而集中分布，出现图2中算例01所示聚集现象。但核函数近似的影响域有限大，若2个粒子速度差异较大而距离较远，则难以相互影响，也会产生相对孤立的碎片，形式上表现为碎片云。

综上，不引入失效模型也能得到相对孤立的碎片，但只是形式上表现为碎片云，材料表现与实际不符；引入失效模型后粒子点失效表现才符合物理实际，得到的碎片分布符合实验结果。

2.2 最大拉应力及Grady失效模型结果比较

进一步考虑，最大拉应力模型中材料失效阈值恒定，但Grady模型中随着材料当前状态的改变，阈值ps的计算值也会变化。图4示例了2种失效模型下某粒子点处失效阈值变化及主应力失效规则的触发，可见Grady模型下失效阈值在冲击波到达后开始剧烈变化，事实上主要随屈服强度变化，密度和体积声速随时间变化不大，而粒子点在最大主应力超过失效阈值后立即被判为失效，应力值归零。

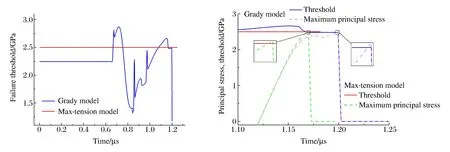
图4 材料失效阈值变化及对应失效规则触发的示例Fig.4 An instance of material failure regulation and its failure threshold-time curve

在算例02和算例03中取不同位置处C、D、E等3个测量点，如图5所示为3个点处压力时间历程，比较2种失效模型下粒子点失效表现的差异。C点粒子在Grady和最大拉应力模型下同时失效，但最大拉应力模型下负压更大；D点粒子在最大拉应力模型下负压也更大，而且比Grady模型下更晚失效；E点粒子在Grady模型下失效，但在最大拉应力模型下未失效。

由图3可见算例02中B点未失效，但其负压峰值远低于无失效模型的算例01下，可见其他粒子的失效导致的压力变化会影响B点压力，失效准则的引入降低了粒子点负压；无失效模型情况可视为粒子最难失效情况(不失效)，结合图5中最大拉应力模型下粒子点负压大于Grady模型下，由此推断：材料更难失效的失效模型下粒子负压更大。从粒子失效时间可得到相近结论，更难失效的模型下粒子更晚失效甚至不会失效。

综上，从粒子点压力表现来看，在本文所采用失效参数下，最大拉应力模型下材料更难失效。

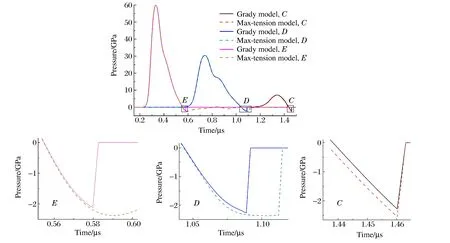
图5 测量点C、D、E压力时间历程Fig.5 Pressure-time curves of gauge points C, D and E

3 碎片数量分布差异

3.1 碎片数量分布的整体比较

粒子失效后成为断裂点，孤立碎片的边界必然全是已失效粒子，AUTODYN软件基于此进行碎片识别，获得SPH粒子和碎片的对应关系及碎片特征。本文中利用AUTODYN碎片识别功能，统计数值模拟结果中正向运动的弹丸碎片数量、质量。由于不引入失效模型的方案明显与实验不符，此处只对算例02～07进行比较，分析最大拉应力模型和Grady模型下结果的差异。

统计模拟结果中所有碎片，发现3个工况中Grady模型下碎片总数分别比最大拉应力模型下多1.78%、4.48%、0.42%，碎片越多意味着失效粒子越多，这说明Grady模型下材料更易失效。因此，从碎片总数来看，在本文所采用失效参数下，最大拉应力模型下材料更难失效。

统计质量大于0.01 mg的弹丸碎片，得图6所示对数坐标下碎片无量纲质量m/M与累计数量Nc的关系，其中Nc为质量不小于m的碎片累计数量，M为0.01 mg以上碎片总质量，3种工况下依次取683、936、340 mg。需要注意，对数坐标下坐标分布非线性，小质量碎片段差异被压缩。不同模型下曲线变化速度有差异，导致不同质量处碎片累计数量相对大小不一，lg(m/M)=-2.9标记线起不同模型下曲线基本一致，直到lgNc=1.1所标记的大碎片段位置。

从曲线整体来看，2种模型下曲线变化趋势一致，各工况中Grady模型下曲线均接近直线，而最大拉应力模型下曲线波动大，偏离直线。不同工况下材料强度及冲击波强度等不同，Grady模型能够很好地与撞击工况自适应，对应的调整失效阈值而在对数坐标下呈现出更好地线性分布，表现更佳。

3.2 大质量碎片分布差异比较

图6中2种模型下曲线lgNc=1.1的大碎片段差异明显，3种工况中均呈现Grady模型下碎片质量先更大后更小的规律。分析碎片位置发现Grady模型下将最大的若干个大碎片的部分材料分给了稍小的大碎片，使大碎片段质量分布更平缓。最大拉应力模型下粒子更聚集，导致最大的个别碎片偏大，其他大碎片偏小。另外，各工况中均为Grady模型下碎片总数更多，但在分界线处碎片数量基本一致，说明最大拉应力模型下是小碎片数量偏少。这同样是最大拉应力模型下材料难失效导致，小碎片附着在大碎片上未剥离，小碎片数量大幅减小，同时增加大碎片质量。

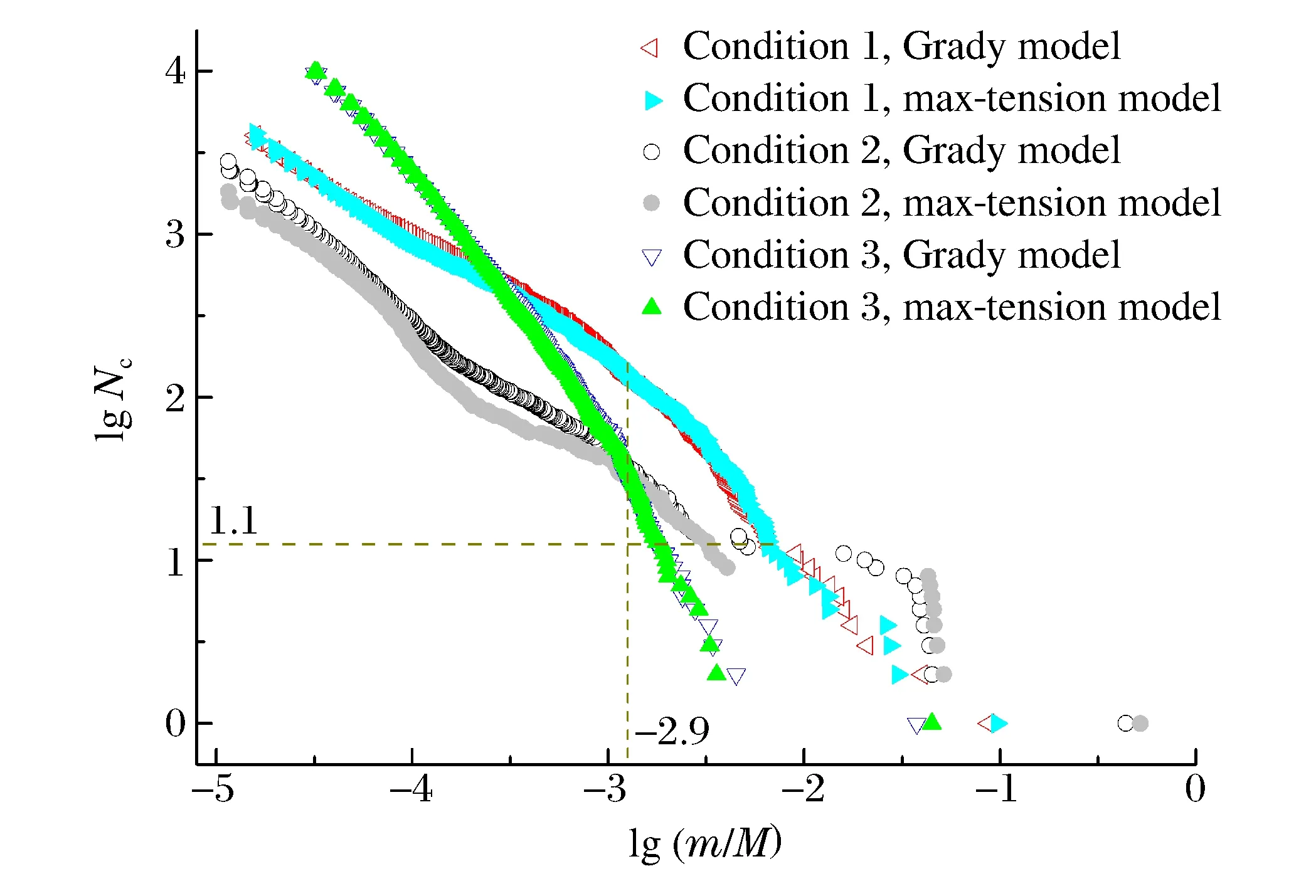
图6 0.01 mg以上碎片累计数量分布Fig.6 Distribution of cumulative number of debris above 0.01 mg

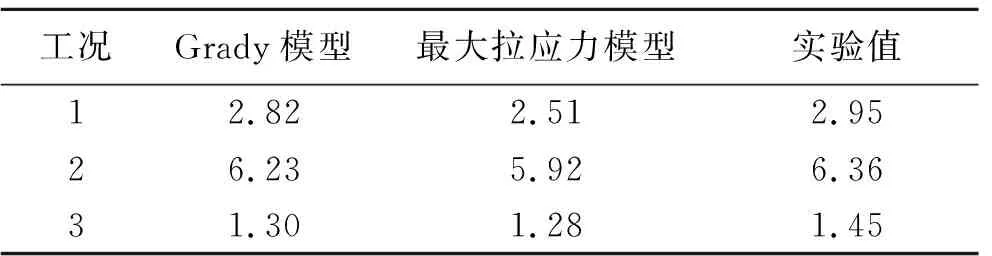
工况Grady模型最大拉应力模型实验值12.822.512.9526.235.926.3631.301.281.45

最大碎片的侵彻性能可代表碎片云的侵彻极限，比较发现：各工况中Grady模型下最大碎片的质量分别比最大拉应力模型下小9.84%、18.5%、19.2%，而轴向速度基本一致。综上可推断：Grady模型下得到的碎片云侵彻极限更小，对后续靶板的损伤更均匀；最大拉应力模型下后续靶板损伤更严重。

测量计算结果中最大碎片在各坐标方向尺寸并计算其球等效直径，如表2所示为最大碎片球等效直径计算值与实验值的对比。虽然最大拉应力模型下最大碎片的质量较大，但由于其粒子聚集度高，碎片等效直径却稍小。不难看到，所有工况中Grady模型下最大碎片等效直径计算值更接近实验值，Grady模型计算结果更符合实验。

4 失效模型影响随撞击工况变化

根据各工况板厚及撞击速度可知，工况1下材料初步破碎，工况3下材料充分破碎，工况2介于前两者之间。观察图6中各工况下两曲线间的差异，材料破碎越充分，曲线间差异越小，失效模型方案对计算结果影响越弱，从碎片总数也能得到此结论。

从材料失效考虑，当材料破碎不充分时，稀疏波强度与失效阈值相当，因此失效阈值上细微的差别就能导致很大的碎片分布差异；材料破碎充分时，稀疏波强度远大于失效阈值，失效模型影响便较弱。另外，Grady模型中失效阈值主要随材料屈服强度改变，撞击较弱时应变、应变率等较小，导致失效阈值计算值偏小。Grady模型下材料本就更易失效，更加偏小的失效阈值就会和最大拉应力模型下恒定的阈值差距更大，加剧两种模型下碎片分布差异。

撞击速度对稀疏波强度影响显著，工况2撞击速度远低于工况1，而工况3的稍大于工况1。因此，工况2相比于工况1和3，不同失效模型下碎片数量曲线之间差异明显，且最大碎片显著减小。板厚主要改变强稀疏波作用时长和作用区域大小，严重影响小碎片数量，但弹丸材料总量不变，导致工况3下碎片总数显著增大，曲线斜率明显变化，但对曲线间差异影响不明显。

从细观上分析失效模型方案对粒子点失效的影响，在弹丸和薄板模型中轴线遍布测量点，图7为只在一种失效模型下失效而在另一种模型下不失效的测量点的轴向坐标Z，0点到弹丸尾端和薄板背面等距。图7中不同模型下失效表现相反的最远粒子的坐标，表征了失效模型对材料失效表现产生明显影响的起始位置。工况2中表现相反的最远粒子坐标最大，工况3中则坐标最小，正是上述的稀疏波强度和失效阈值的比较。工况2下初始稀疏波强度即和失效阈值相当，边缘位置处失效模型的影响已展现出；工况3下需要稀疏波不断衰弱直至中心附近才能表现出失效模型的影响；工况1下最远粒子坐标与工况3接近而与工况2差距较大，主要是由撞击速度的差异导致的。

值得关注的是，图6中大碎片段碎片质量出现明显分歧，但开始分歧位置均在lgNc=1.1标记线附近，说明撞击工况对大碎片段差异大小影响弱。大碎片多靠近弹丸中心，材料不断层裂破碎同时降低稀疏波强度，导致大碎片位置时稀疏波强度均较低，因此撞击工况对大碎片段差异影响不显著。

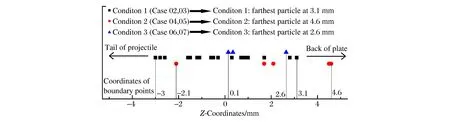
图7 模型中轴线上不同失效模型下失效表现不同的粒子点Fig.7 Particles with different failure performance under Grady and max-tension models

5 失效阈值对碎片云的影响

Grady模型中临界应变常数εc直接影响失效阈值计算值，其对所有材料被建议取值0.15[7]，对于铝合金材料已被验证该取值较为适用。考虑到铜材料实验失效应力为1.0～2.5 GPa，而εc=0.15时Grady模型计算值仅为1.0 GPa[7]，因此本文以OFHC为例，尝试εc=0.15,0.30,0.45和0.60，考察失效阈值对碎片云的影响，同时确认铜材料合适的εc取值。

第2部分算例参照实验[8]取直径7.72 mm、厚2.36 mm的OFHC圆盘正撞击1 mm厚的6061-T6铝薄板，弹速为6.39 km/s，圆盘轴线与速度方向呈4.6°夹角，采用Shock状态方程和Steinberg-Guinan强度模型。

图8为圆盘中心粒子失效时刻压力的变化曲线，随着εc增大，粒子负压增大且更晚失效。临界应变常数εc越大，失效阈值越大，材料越难失效。比较碎片云特征速度发现：随着εc增大，碎片云最前端速度减小1.3%，最外侧径向速度减小3.5%，失效阈值的增大导致碎片云扩散程度下降。但由于边缘位置稀疏波强度很高，失效阈值对碎片云速度影响非常小。事实上，各εc取值下模拟的碎片云扩散程度均不及实验，因此εc=0.15时速度结果最接近实验，但不同取值时碎片云特征速度变化不超过3%，合适的εc取值需要根据具体算例中其他材料参数和人工黏性等确定。

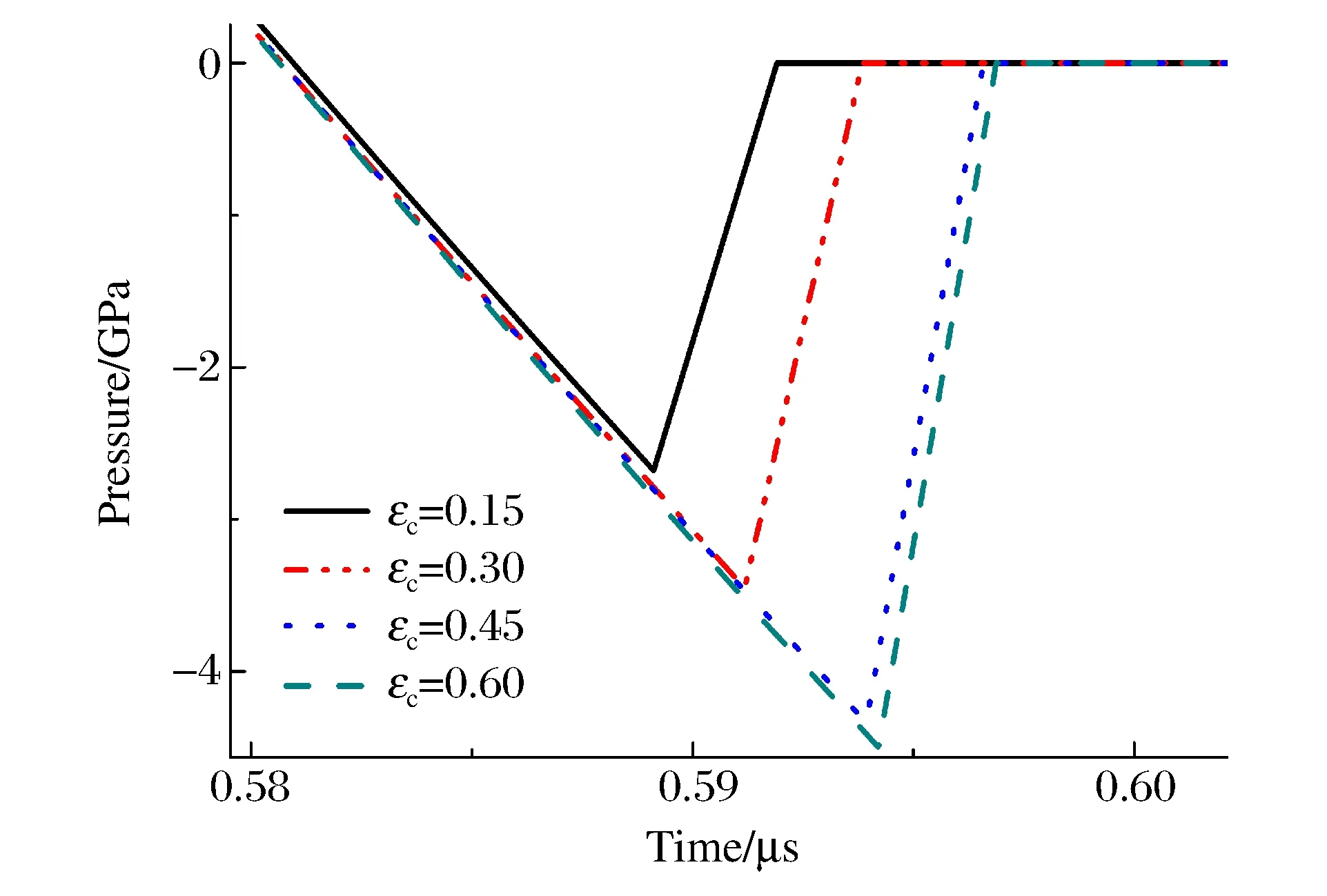
图8 圆盘中心粒子失效时刻压力的变化Fig.8 Pressure-time curves of the center particles of the disc projectile

εc碎片总数最大碎片/mg0.15177 83214.430.30161 61622.230.45152 95631.210.60145 48034.14

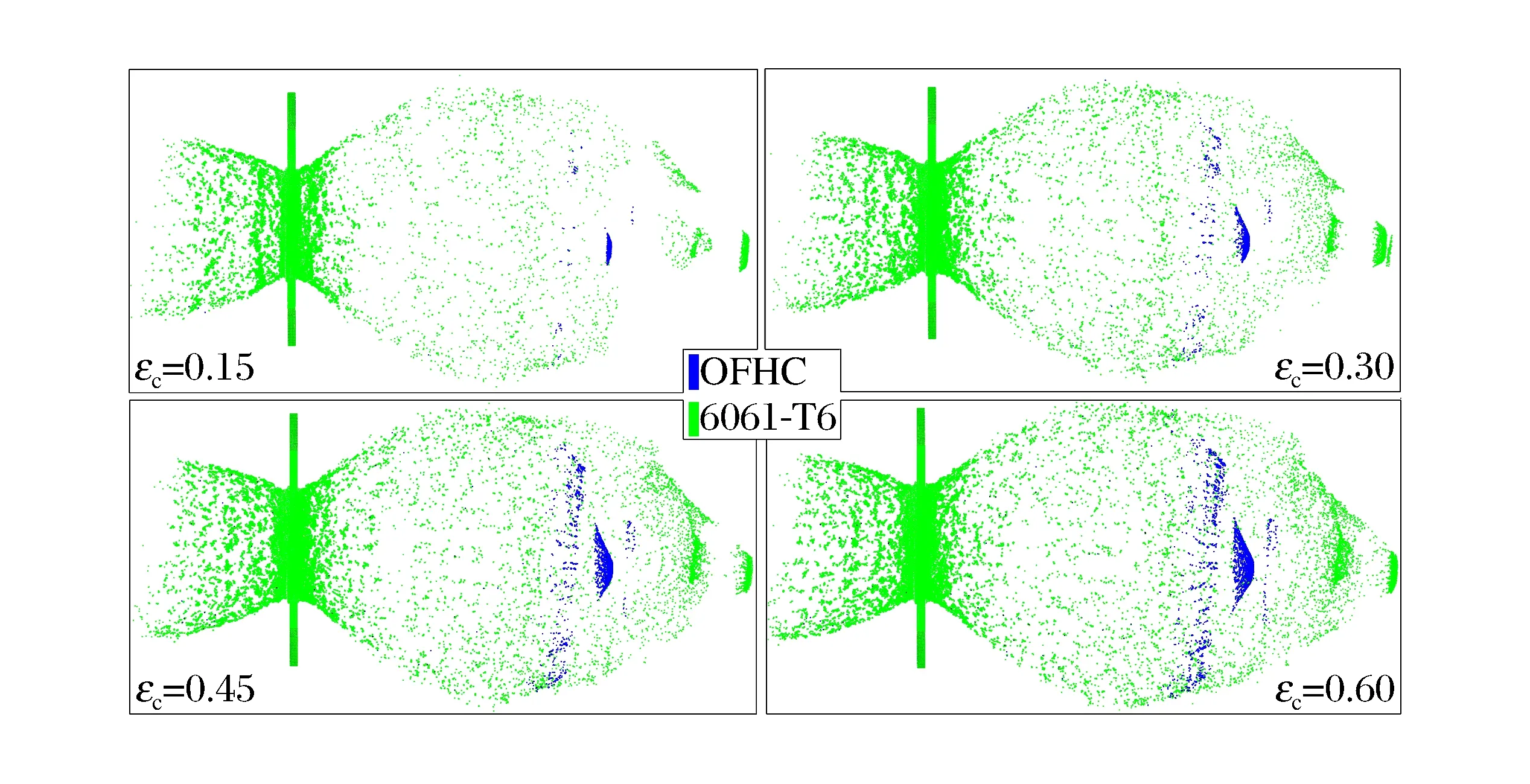
图9 碎片云碎片识别结果侧视图Fig.9 Side view of debris recognition result of debris clouds

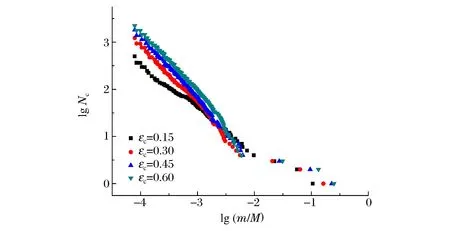
图10 0.01 mg以上碎片累计数量分布Fig.10 Distribution of cumulative number of debris above 0.01 mg

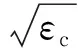
综上，增大Grady模型下临界应变常数εc直接导致材料更难失效，宏观表现为碎片云扩散程度小幅减弱，碎片总数减少但0.01 mg以上碎片增加，最大碎片质量明显增大，和前文中采用最大拉应力模型导致的材料更难失效表现基本一致。

6 结 论

比较发现，不引入失效模型时，材料在强负压下不断裂的表现不符合物理实际，弹丸碎片中粒子高度聚集，与实验结果严重不符。因此，碎片云数值模拟中必须引入材料失效模型。有失效模型时，从碎片识别图像、碎片分布曲线及最大碎片尺寸来看，Grady模型计算结果更符合实验。不过失效模型对碎片云的影响程度与撞击工况相关，材料破碎越充分，不同失效模型下碎片分布曲线之间差异越小。

在本文所用失效参数下，最大拉应力模型下材料更难失效，导致碎片云扩散程度小幅减弱，小碎片聚集为大碎片，大碎片质量变大，碎片云侵彻极限提高。增大失效阈值同样导致材料更难失效，亦有上述表现。