钢化玻璃冲击波毁伤效应测试结果分析*

钟 巍,寿列枫,何 增,李伟昌,雷 鸣,刘 俊,田 宙,浦锡锋,王仲琦

(1.西北核技术研究所,陕西 西安 710024; 2.湘潭大学材料科学与工程学院,湖南 湘潭 411105; 3.北京理工大学爆炸科学与技术国家重点实验室,北京 100081)

现代城市建筑中幕墙类结构(包括玻璃幕墙、陶瓷幕墙、金属幕墙等)的使用率越来越高，玻璃幕墙结构在所有幕墙类结构中又最受青睐。玻璃幕墙装饰作为一种融建筑技术、建筑功能，以及建筑艺术为一体的建筑外维护构件，是建筑物的高级装修，在世界各国的高层标志性建筑中被广为采用[1]。尽管玻璃幕墙有着上述诸多的优点，但面对目前世界各地恐怖主义爆炸袭击和各种意外爆炸事件时有发生的情况[2-4]，玻璃幕墙在各种爆炸荷载下的抗爆性能直接影响着城市人员的人身安全，大量的实地调查及分析发现在各种爆炸事故中建筑玻璃破碎产生的碎片及爆炸冲击波的冲击是造成人员伤亡的主要原因[5]。近年来对玻璃幕墙抗爆性能的研究成为爆炸效应和建筑安全领域的研究热点。例如，Zhang等[6]开展了较大的钢化玻璃在受到爆炸冲击波作用后产生的玻璃碎片特性的实验研究，详细地给出了实验中玻璃碎片的尺寸分布、飞散速度等规律，他们在实验研究中发现钢化玻璃在受到爆炸冲击作用产生的碎片中也会存在较锋利的玻璃碎片，这些碎片在飞散过程中容易对人员或一些设施造成较严重的伤害。Zhang等[7]还针对多层安全玻璃受到爆炸冲击波作用的问题开展了数值模拟研究，通过大量的数值模拟，给出了多层安全玻璃在受到冲击波作用后重要参数的研究结果，并提出了预测玻璃毁伤超压和冲量阈值的p-I曲线[7]。美国的Baker工程与风险研究机构在美国军方的委托下开展了大量的冲击波毁伤玻璃效应实验，他们利用大型激波管产生冲击波作用于钢化玻璃，研究钢化玻璃的响应情况，并通过与专业的玻璃响应研究理论分析软件WINGARD进行对比，分析了不同种类玻璃在实验室严格的安装条件下的毁伤情况[8]。但这些研究大多是针对某种单一的玻璃或者采用便于实验实施的玻璃安装方式开展的偏学术性的研究，可供实际工程应用的规律性的研究结果还比较匮乏，因此，亟需开展更多玻璃种类和更多安装方式的研究。为了研究不同厚度、不同种类(不带夹层/带PVB夹层)的钢化玻璃，在不同安装方式下的冲击波毁伤效应，获取毁伤阈值、毁伤规律和碎片分布规律，我们开展了一系列的钢化玻璃冲击波毁伤效应外场化爆实验。本文将介绍系列实验的全部冲击波参数测试情况，包括冲击波参数测试、测试结果的分析处理、冲击波关键参数(正反射超压、冲击波到时、正压作用时间、正反射冲量等)的实验值及其与CONWEP计算结果的比较。此外，还将比较冲击波正反射参数和负反射参数，分析毁伤钢化玻璃的主要冲击波参数，以期为后续钢化玻璃冲击波毁伤效应的研究提供基础。

1 钢化玻璃冲击波毁伤效应实验简要介绍

历时3年在不同的季节和天气条件下共开展了3轮实验。第1轮和第3轮实验分别在冬季和夏季进行，天气条件都非常理想，没有起风，对冲击波参数测试影响较小；第2轮实验是在春季进行的，实验现场有一定的风，这可能会对冲击波参数测试造成一定的影响,这一点在本文后面的冲击波测试参数分析中将会进一步说明。

实验中使用的爆炸装药是按制药标准灌制而成的柱形TNT裸药，装药密度为1 640 kg/m3，分5 kg和10 kg两种。为了保证爆心与钢化玻璃正中心位于同一水平面，将TNT装药自由放置在高度与钢化玻璃正中心相同的塑料方凳上。实验中使用的钢化玻璃均是按照《玻璃幕墙工程技术规范JGJ102-2003》[9]加工制造的。各发次实验使用的TNT装药及玻璃尺寸等具体信息如表1所示,W为TNT的质量，σc为玻璃的表面压应力，l、w、h分别为玻璃的长度、宽度和厚度。本文中约定实验序号“×-×-×”中第1个数字表示实验轮次，第2个数字表示在当轮实验中实验的发次，第3个数字表示在整个系列实验中的发次。

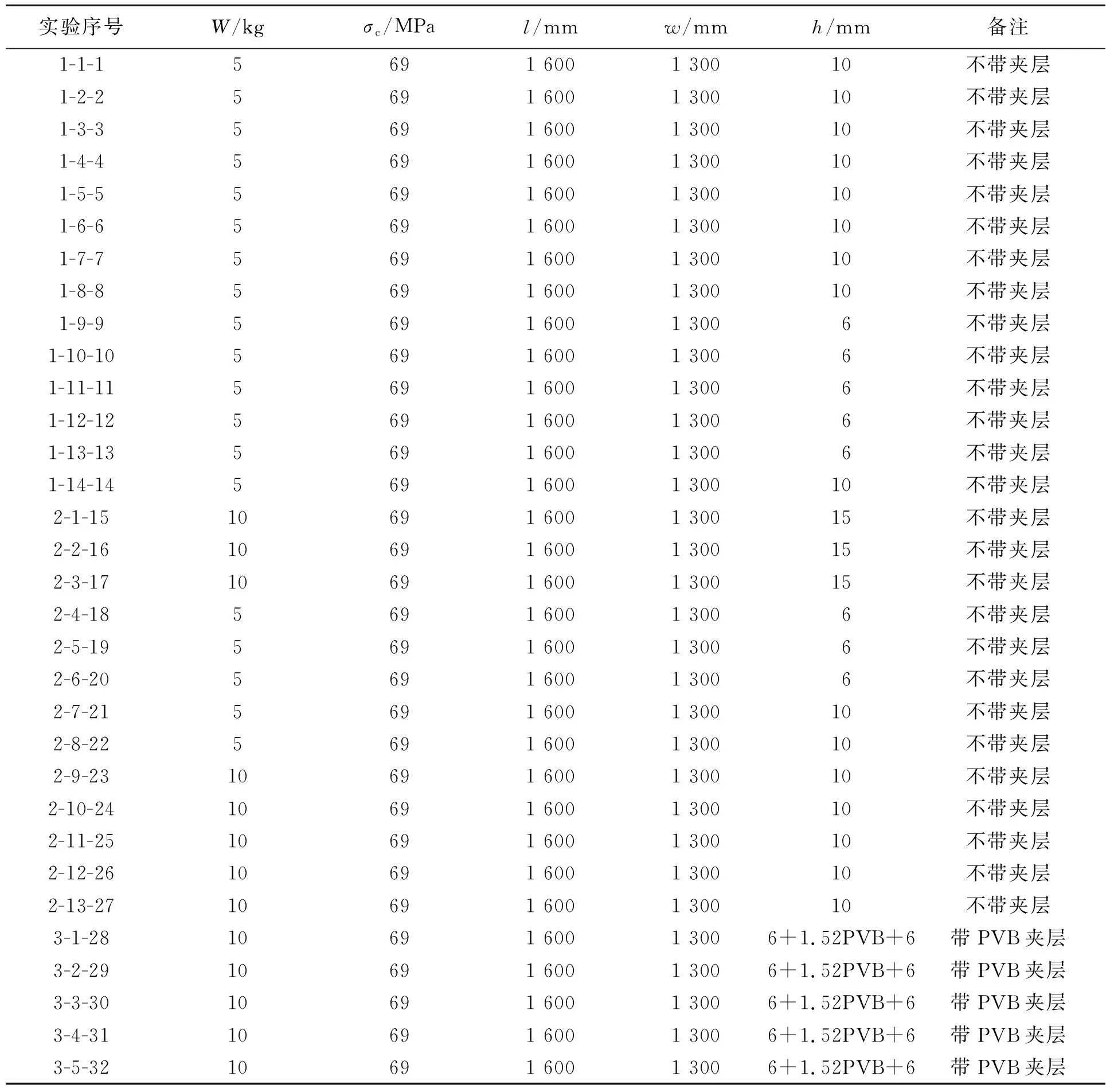
表1 实验中使用的TNT装药和玻璃的基本信息Table 1 Basic information of the TNT charge and glass in each experiment

2 冲击波参数实验测试方法与CONWEP程序计算爆炸参数

为了确保通过实验获得的钢化玻璃冲击波毁伤阈值的准确性，需要对冲击波实验测试结果进行校验，保证实验中测试得到的冲击波参数正确可靠。通过将实验测试结果与CONWEP计算结果进行对比，验证实验测试结果的正确性。

2.1 实验测试方法

实验中安装了PCB压力传感器用于测试冲击波反射超压时间历程。PCB压力传感器的型号为LW27081，其安装在玻璃安装框架旁边，位于同一平面的高强度防爆水泥墙面上，传感器正面对着装药方向，如图1所示，图中所示的防爆水泥墙是按超高防爆性能的标准浇制的，其强度足够保证冲击波测试不会受到来自水泥墙的影响。同时，由上一节中TNT装药的安装方式可知，TNT装药与PCB压力传感器之间存在一个较小的角度，将在后文中证明，这个角度对测试结果造成的误差是可以接受的。

图1 PCB压力传感器的安装Fig.1 Installation of PCB pressure sensor

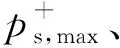
图2 理想爆炸超压时间历程曲线及其三角形简化模型Fig.2 The ideal explosion shock wave overpressure-time curve and the triangle simplification model

根据图示简化模型，可得爆炸超压计算公式：

(1)

由图2和式(1)易得简化模型下正、负反射冲量的计算公式：

(2)

2.2 CONWEP程序计算爆炸参数

CONWEP是一款根据TM5-855-1[10]编写的常规武器重要爆炸参数计算程序，可准确高效地计算各种爆炸荷载，包括TNT装药外场爆炸实验。CONWEP程序计算结果的可靠性得到了爆炸力学领域的高度认可[11-13]，并且已经被内嵌到大型有限元软件LS-DYNA中[14]。

本文中使用CONWEP程序计算得到了每一发实验条件下的主要冲击波参数，包括正反射超压、冲击波到时、正压作用时间和正反射冲量等，并根据CONWEP程序保存的爆炸冲击波超压随时间变化的数据文件绘制了正反射超压时间历程曲线。

2.3 用PCB压力传感器测量得到的结果作为钢化玻璃上冲击波参数合理性的证明

图3 爆炸冲击波传播示意图Fig.3 A diagram of the blast shock propagation

由于所选用的PCB压力传感器无法直接安装在钢化玻璃上，如前所述，将PCB压力传感器安装在与玻璃处于同一竖直平面的水泥墙上。下面将证明，在工程误差允许的范围内，用实验中采用的PCB压力传感器安装方法得到的冲击波参数测量结果作为钢化玻璃上的冲击波参数实验结果是合理的。

实验中TNT装药爆炸产生的爆炸冲击波是一个球面波，图3给出的是位置P处的TNT装药爆炸后产生的冲击波传播到钢化玻璃及PCB压力传播器的示意图。图3中OP为爆心距，O为玻璃的中点，由于玻璃宽度为1.3 m，因此，OB和OC的长度均为0.65 m。实验中测得AB的长度为0.13 m，因此OA的长度为0.78 m。显然，当给定爆心距OP的值，由图中几何关系容易计算得到位置A、B、C处的爆心距。

于是，当知道TNT装药质量的情况下，可以用CONWEP程序计算得到O、A、B、C处的冲击波参数，不同条件下的计算结果如表2所示，其中由于对称关系，位置B和位置C的计算结果相同。

观察表2发现，在不同的装药质量和不同的实验爆心距(图3中的OP)条件下，位置A、B、C处的冲击波参数CONWEP计算结果与位置O处的结果相对误差很小，完全在可以接受的误差范围之内,这里认为在工程上15%～20%的相对误差是可以接受的。对于实验爆心距为4.000 m的情况，由于只进行了一发TNT质量为5 kg的实验，因此，表2中没有给出TNT装药质量为10 kg时的CONWEP计算结果。

表2 位置O、A、B、C处的冲击波参数计算结果Table 2 Calculation results of shock wave parameters for locations O, A, B and C

3 各发实验冲击波参数测试与CONWEP计算结果

3.1 冲击波正反射参数实验结果与CONWEP计算结果的比较

下面将冲击波实验测试结果与CONWEP计算结果进行比较。

3.1.1爆炸冲击波正反射超压时间历程曲线比较

由于总的实验发次较多(共进行了3轮合计32发实验)，这里从每轮实验中选取2发实验，使用CONWEP程序计算各发实验对应的TNT当量和爆心距条件下的爆炸冲击波参数，并与实验结果一起作正反射超压时间历程曲线比较，如图4～6所示。

图4 第1轮实验正反射超压时间历程曲线与相应的CONWEP程序计算结果的比较Fig.4 Comparison of the normally reflected overpressure-time curves obtained in the first round experiments with the corresponding ones computed by CONWEP

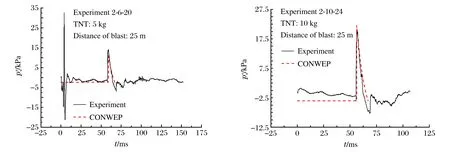
图5 第2轮实验正反射超压时间历程曲线与相应的CONWEP程序计算结果的比较Fig.5 Comparison of the normally reflected overpressure-time curves obtained in the second round experiments with the corresponding ones computed by CONWEP

图6 第3轮实验正反射超压时间历程曲线与相应的CONWEP程序计算结果的比较Fig.6 Comparison of the normally reflected overpressure-time curves obtained in the third round experiments with the corresponding ones computed by CONWEP

3.1.2爆炸冲击波正反射基本参数比较

表3～5详细列出了3轮实验中爆炸冲击波正反射基本参数(包括正反射超压、冲击波到时、正压作用时间和正反射冲量)实验测试结果与CONWEP程序计算结果的比较。

表3中，第1-8-8发实验测量数据与CONWEP程序计算结果误差非常大，结合第1-5-5和第1-7-7发实验可以判断第1-8-8发实验测量结果不准确。考虑到第1-5-5和第1-7-7发实验的冲击波参数已经非常接近，已达到工程上可以接受的误差范围，为了计算方便，根据“以直代曲”的思想，使用线性插值取第1-5-5和第1-7-7这2发实验测量结果的平均值作为第1-8-8发实验的测量结果修正值。从表中还可以发现，第1-14-14发实验正反射冲量实验测量结果与CONWEP程序计算结果误差较大，考虑到该发实验爆心距很小，实验现场观察表明玻璃在爆炸冲击波作用下很快就破碎并往后飞散，即这种情况下对玻璃起毁伤作用的主要是正反射超压，正反射冲量此时对玻璃的毁伤几乎没有影响。因此，对于表中第1-14-14发实验正反射冲量实验测量结果与CONWEP程序计算结果误差较大这个现象可以忽略。另外，表中第1-2-2和第1-12-12发实验条件完全相同，但第1-2-2发实验的冲击波参数测量结果与CONWEP程序计算结果之间的误差明显大于第1-12-12发实验，我们认为第1-2-2发实验的测量可能存在问题，这里取第1-12-12发实验的测量结果作为该比例爆心距的实验结果。

除上述3发实验外，在不考虑正压作用时间的情况下，表3中的结果表明实验测量结果与CONWEP程序计算结果非常吻合。显然，CONWEP程序计算结果表明其正反射冲量与正反射超压和正压作用时间不满足式(2)，即CONWEP程序在处理正反射冲量时可能采用了其他的模型，而该模型对正压作用时间的计算进行了修正，以保证正反射冲量计算的准确性。而本文对实验数据中采用式(2)计算正反射冲量的结果与CONWEP程序结果计算的误差很小，从研究冲击波对钢化玻璃毁伤效应的角度看，主要关心超压和冲量的大小，关于这个结果将在本系列研究后续论文中给出证据，因此，可以忽略表3中正压作用时间存在较大误差这一现象。关于前面所提的“CONWEP程序可能采用了不同的模型来计算正反射冲量”这一点，我们正在进行更深入的分析研究，这里暂不赘述。

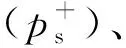
综合表3～5和图7～10的结果，可以认为冲击波压力测试结果与CONWEP程序计算结果是吻合的，即使用实验测量得到的爆炸冲击波参数进行钢化玻璃冲击波毁伤阈值研究是准确可靠的。

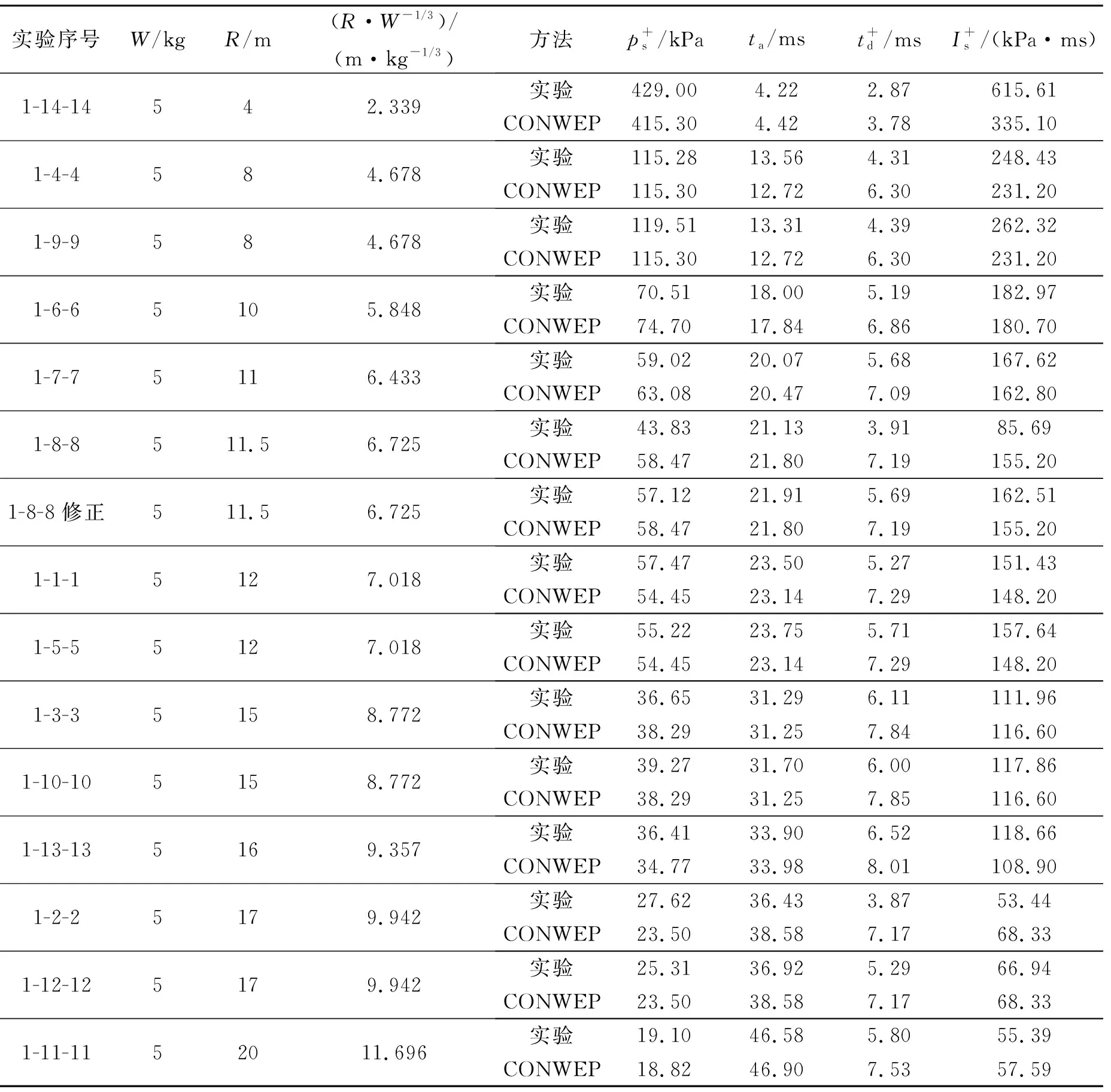
表3 第1轮实验正反射冲击波参数测试结果和CONWEP程序计算结果Table 3 Normally reflected blast parameters obtained in the first round experiments and the corresponding ones computed by CONWEP

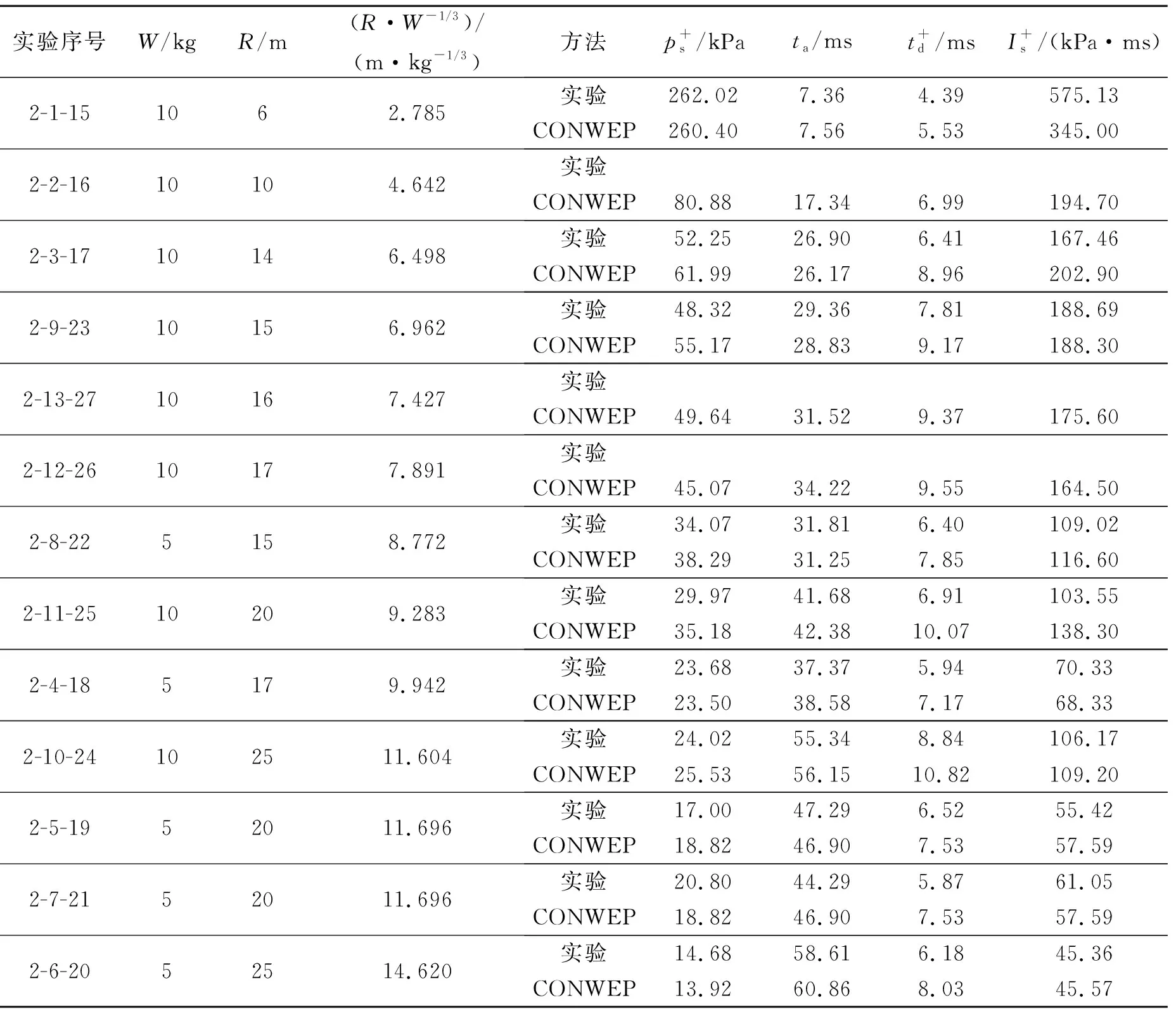
表4 第2轮实验正反射冲击波参数测试结果和CONWEP程序计算结果Table 4 Normally reflected blast parameters obtained in the second round experiments and the corresponding ones computed by CONWEP

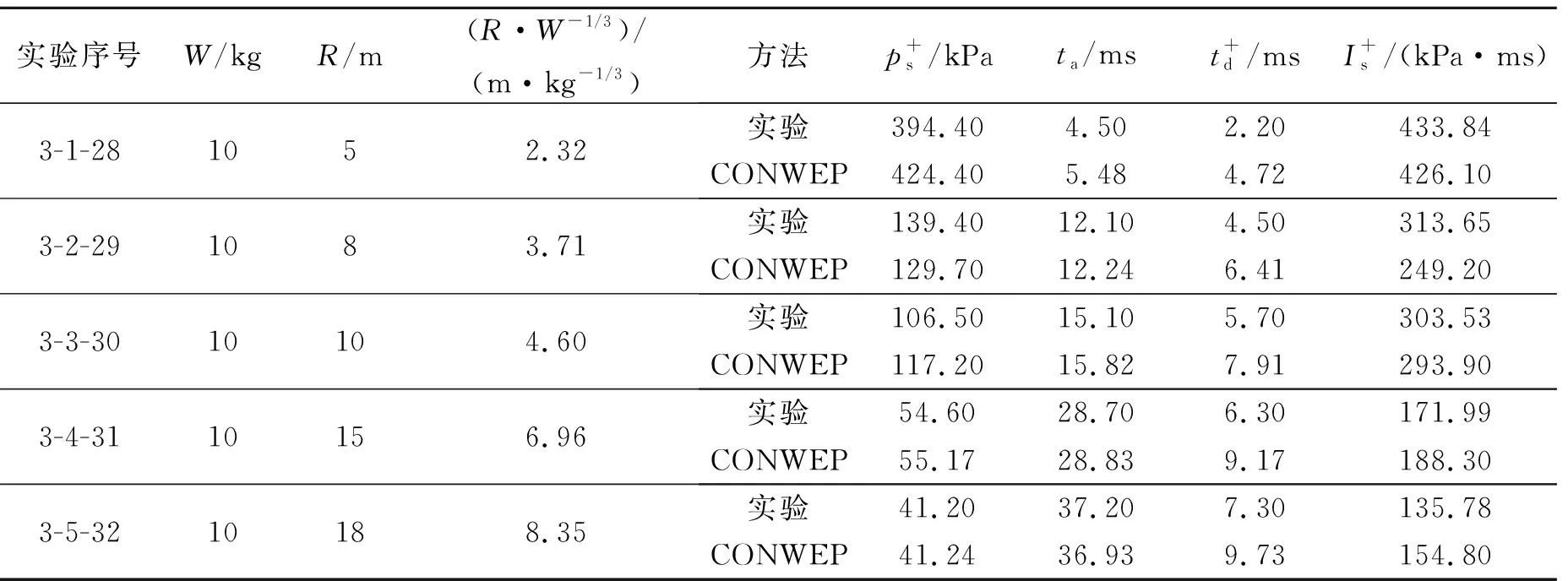
表5 第3轮实验正反射冲击波参数测试结果和CONWEP程序计算结果Table 5 Normally reflected blast parameters obtained in the third round experiments and the corresponding ones computed by CONWEP

图7 正反射超压随比例爆心距的变化Fig.7 Normally reflected overpressure varying with scaled distance of blast

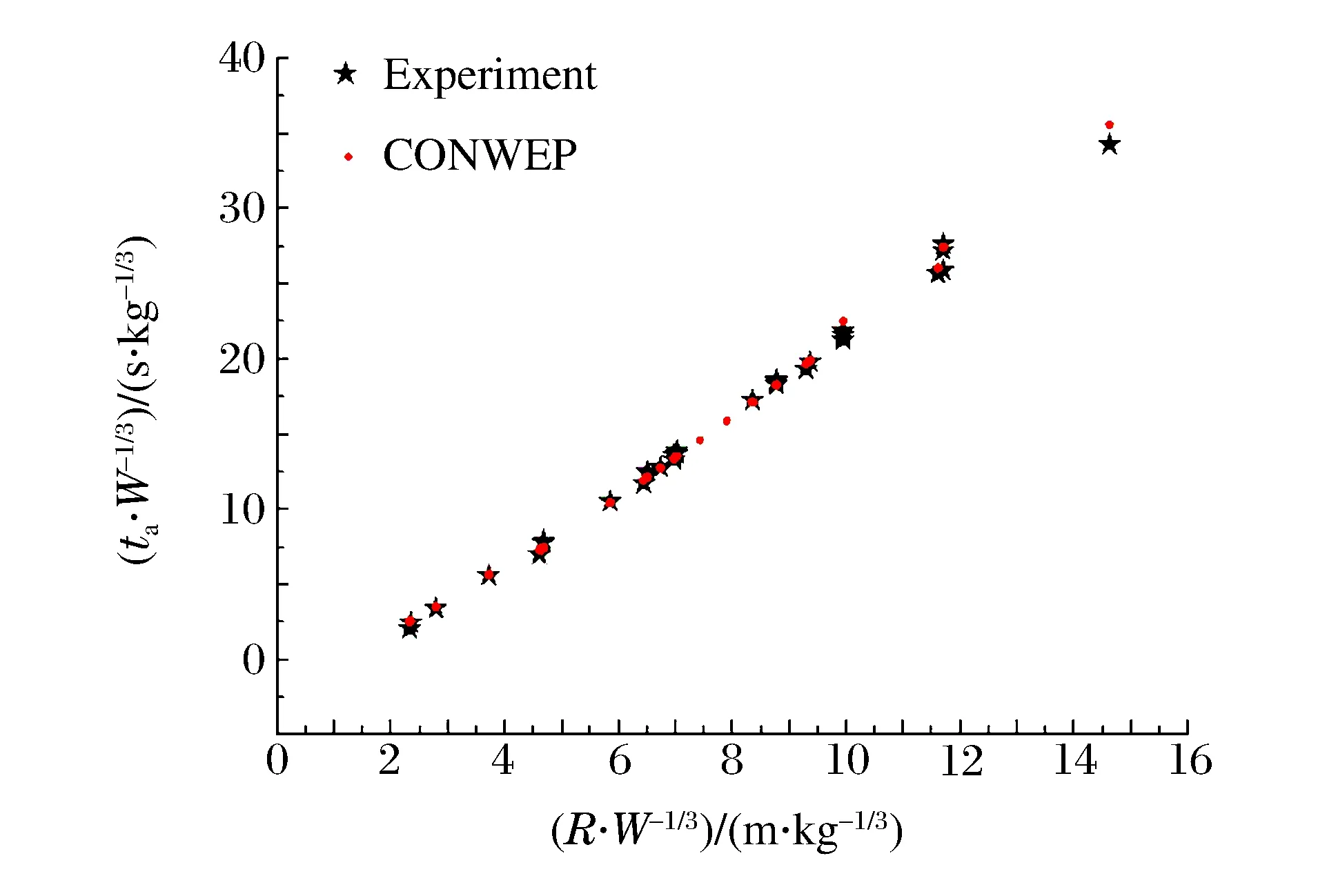
图8 比例冲击波到时随比例爆心距的变化Fig.8 Scaled shock wave arrival time varying with scaled distance of blast

图9 比例正压作用时间随比例爆心距的变化Fig.9 Scaled duration of normally reflected overpressure varying with scaled distance of blast

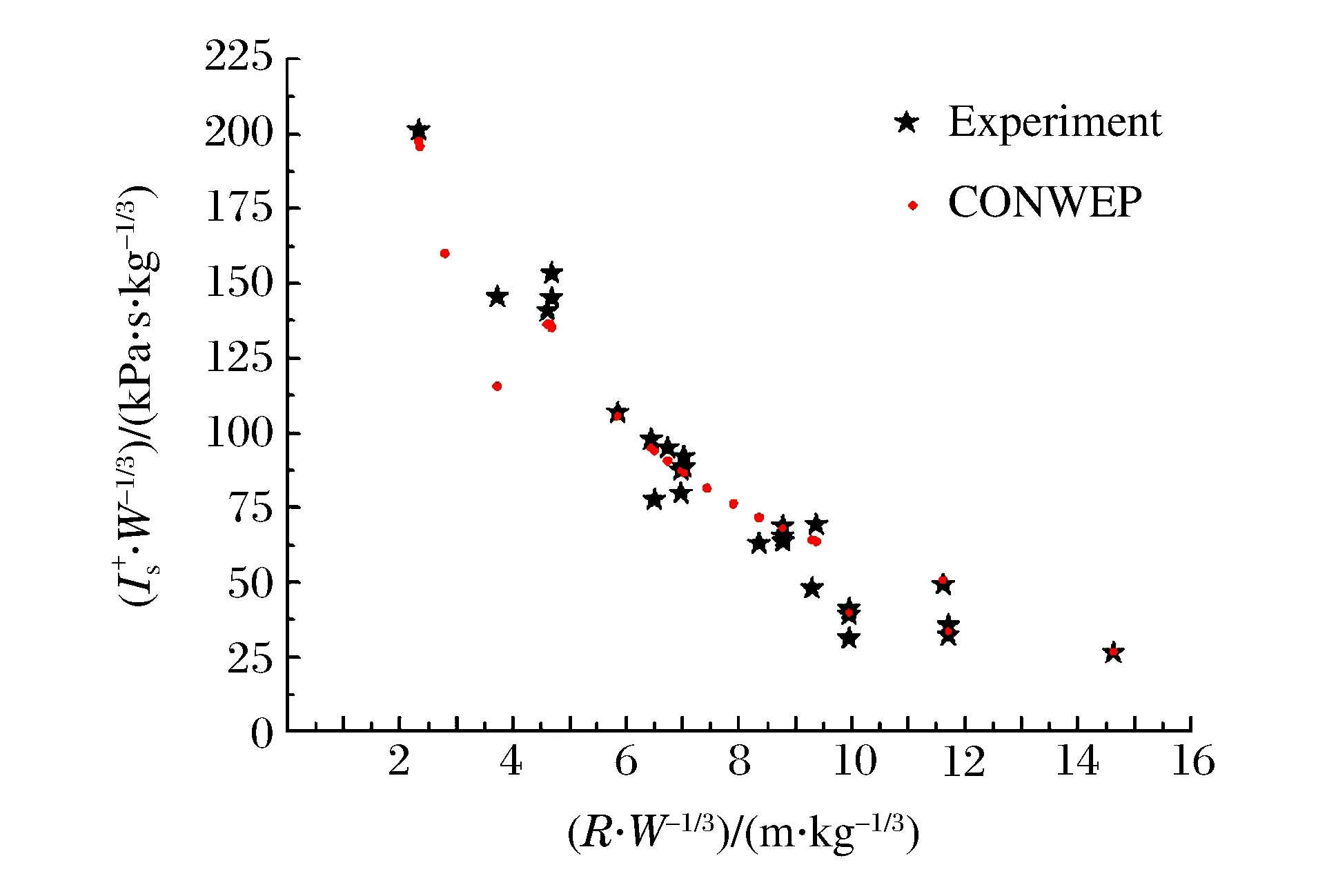
图10 比例正反射冲量随比例爆心距的变化Fig.10 Scaled normally reflected impulse varying with scaled distance of blast

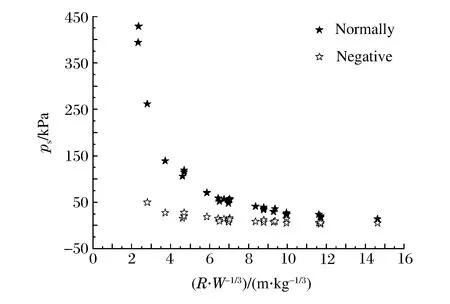
图11 正负反射超压随比例爆心距的变化Fig.11 Normally and negative reflected overpressures varying with scaled distance of blast

3.2 冲击波正负反射参数测试结果对比

取实验测量得到的冲击波超压时间历程曲线上第1个波谷对应的超压值作为负反射超压峰值，负压作用时间取该波谷对应的波脉冲的持续时间，然后按式(2)给出的公式估算负反射冲量。于是，利用实验测量得到的爆炸冲击波超压时间历程曲线(形如图4～6)，估算得到3轮实验的冲击波负反射参数测试结果，如表6～8所示。

根据表3～8，容易作出冲击波正负反射压力测试结果随比例爆心距的变化曲线，如图11～13所示。从图11～13可以看出，爆炸冲击波正反射参数明显高于负反射参数，更重要的是，在高速摄影中清楚地观察到钢化玻璃主要是在受到冲击波正反射作用后产生毁伤的，因此，钢化玻璃的破碎主要是受到爆炸冲击波正反射的作用，与负反射的影响关系不大。同时，结合高速摄影还观察到玻璃在破碎之后碎片的飞散情况，可能会受到冲击波负反射的影响。因此，在后续研究钢化玻璃冲击波毁伤阈值的过程中，主要考虑冲击波正反射，忽略冲击波负反射的影响。

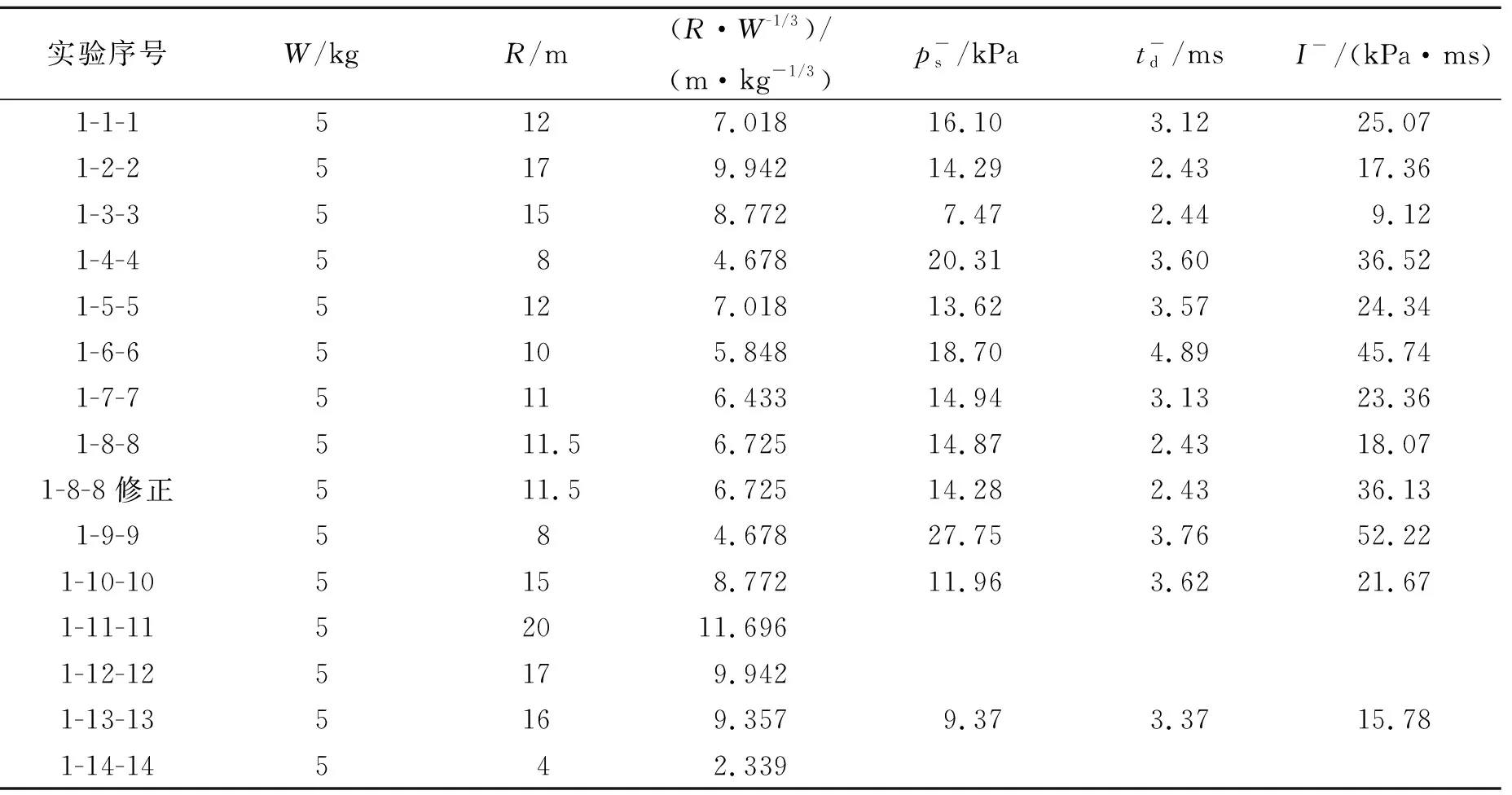
表6 第1轮实验负反射冲击波参数测试结果Table 6 Negative reflected blast parameters obtained in the first round experiments

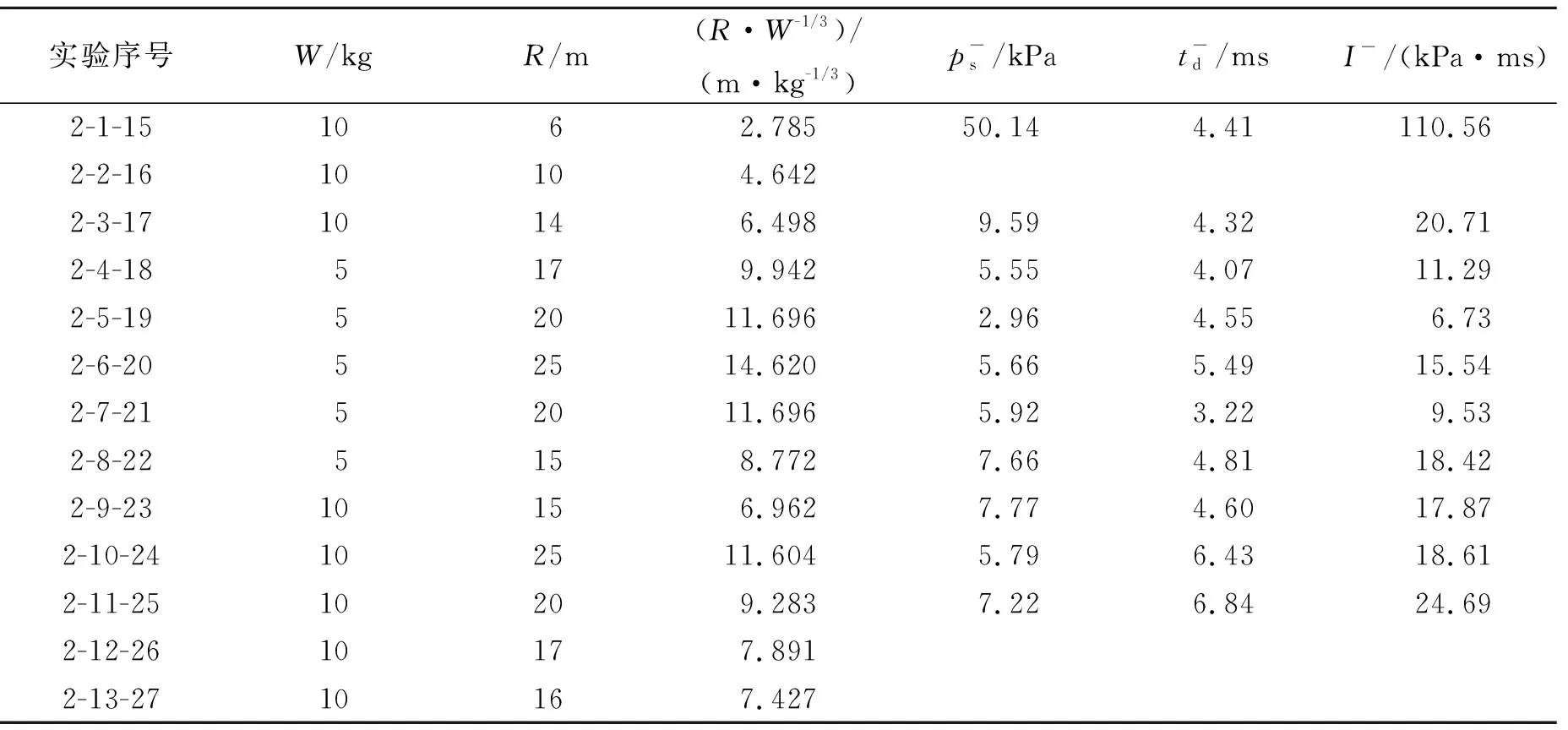
表7 第2轮实验负反射冲击波参数测试结果Table 7 Negative reflected blast parameters obtained in the second round experiments

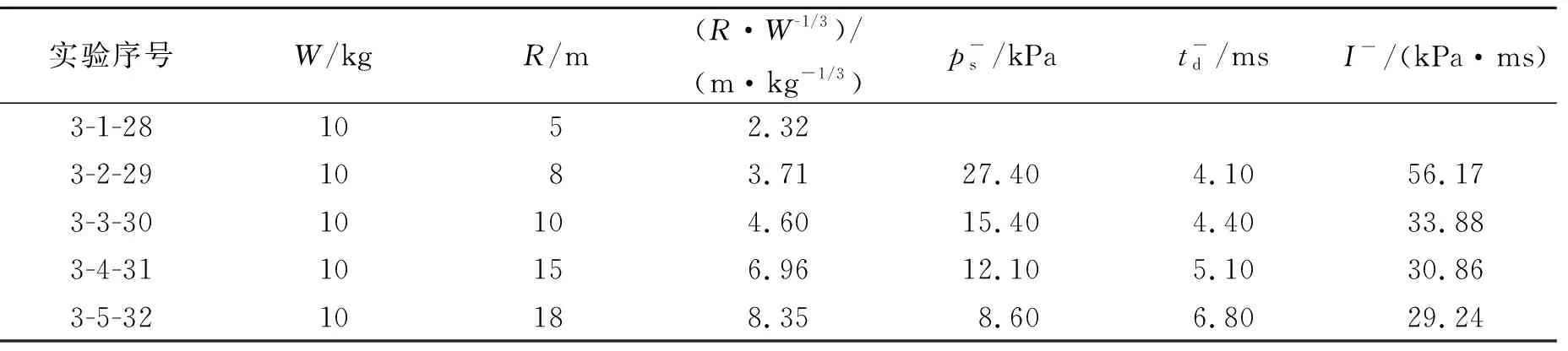
表8 第3轮实验负反射冲击波参数测试结果Table 8 Negative reflected blast parameters obtained in the third round experiments

图12 比例正、负反射超压作用时间 随比例爆心距的变化Fig.12 Scaled duration of normally and negative reflected overpressures varying with scaled distance of blast

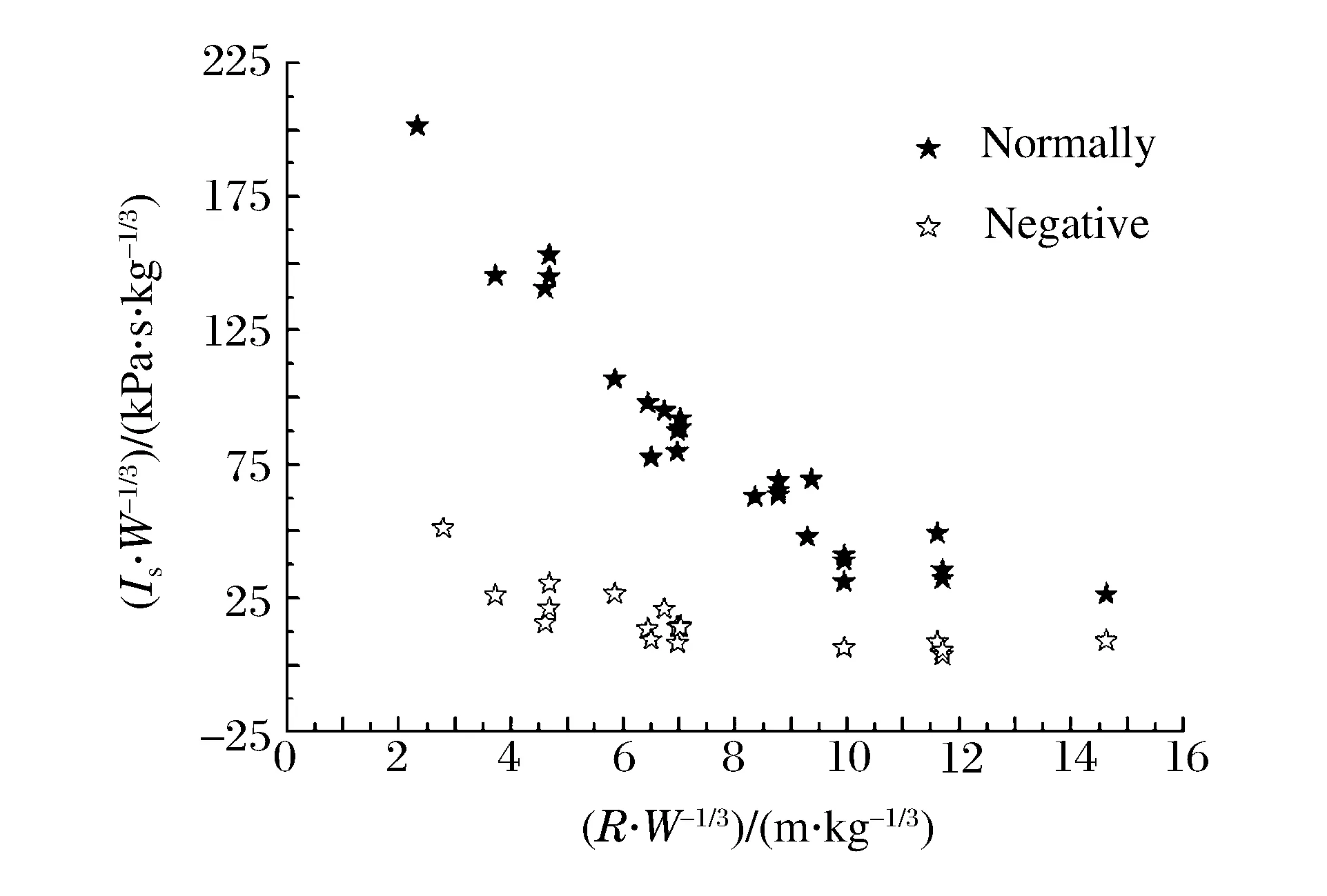
图13 比例正、负反射冲量 随比例爆心距的变化Fig.13 Scaled normally and negative reflected impulses varying with scaled distance of blast

4 结 论

通过对实验中爆炸冲击波参数测试结果的整理，得到了爆炸冲击波基本参数(包括正反射超压、冲击波到时、正压作用时间和正反射冲量等)的实验结果。利用CONWEP程序对每一发实验对应的TNT当量和爆心距进行爆炸冲击波参数计算，将计算结果与实验测量结果作比较，结果表明，实验测量结果与CONWEP计算结果基本吻合，确保了实验测试参数的准确可靠，为后续进行钢化玻璃冲击波毁伤阈值研究奠定了基础。同时，正、负反射冲击波参数对比结果表明，造成钢化玻璃破碎的主要因素是冲击波正反射，冲击波负反射的作用可以忽略。