带环形密闭气囊弹体入水冲击过程的数值分析*

陈 洋，吴 亮，曾国伟，周俊汝

(1.武汉科技大学理学院工程力学系，湖北 武汉 430065； 2.中铁港航-武汉科技大学爆破技术研究中心，湖北 武汉 430065)

缓冲气囊在现代航空航天软着陆技术、重装空投、无人机回收等领域中有着广泛的应用，这些领域的研究成果是缓冲气囊参数设计的重要依据。陈帅等[1]基于热力学和刚体运动学方程，建立了软着陆气囊缓冲过程的理论模型，并结合数值方法分析得出了气囊参数设计的理论依据；温金鹏等[2]在考虑气囊织布弹性势能的基础上，结合能量守恒与热力学基本方程建立了缓冲气囊的简化理论模型，研究发现织物弹性模量、初始充气压力、排气口大小等因素对气囊的缓冲效果均有显著的影响；卫剑征等[3]运用显式有限元软件模拟了气囊展开和缓冲过程，验证了数值模拟方法的准确性。由此可知，关于各类缓冲气囊软着陆过程中冲击特性的研究一直是研究热点问题[4-7]。

入水冲击问题是固、液、气三者相互耦合作用的一种复杂的物理过程[8]。1900年，Worthington[9]利用闪光摄影技术对小球落入不同液体时的飞溅和空泡现象进行了实验观测。最初，研究者主要通过实验研究入水冲击过程，了解入水冲击荷载的规律，随后又逐渐提出了小斜升角模型的近似平板理论、自相似解法等。20世纪中期，各国在航空航天及军事领域开展了大量有关入水冲击的研究，该问题日益受到研究者的关注。

随着数值方法和计算机技术的发展，复杂三维几何结构入水问题也逐渐得到有效解决[10]。近年来，我国学者也对各类结构冲击入水问题中进行了大量的研究工作[11-13]。虽然有关各类结构入水冲击问题的研究成果已经比较多，但是目前针对气囊入水冲击问题的研究仍有欠缺。由于气囊结构的特殊性，气囊入水冲击过程比气囊着陆缓冲过程或者一般结构的入水冲击过程都要复杂的多。例如，在水面对某飞行器进行无动力回收时，在到达水面之前，缓冲气囊迅速充气弹出，飞行器和气囊接触水面缓冲减速，入水之后在浮力的作用下气囊带着飞行器上浮，最终稳定漂浮在水面。以上过程中涉及到囊内气体、气囊壁、囊外液体三者之间复杂的相互作用，对该问题的研究在航空航天、救生、船舶等领域均有重要的实际意义。有鉴于此，本文中基于LS-DYNA，运用控制体积(control volume, CV)法模拟环形密闭气囊，结合流固耦合算法，模拟某飞行器回收入水姿态及减速上浮过程，研究气囊的入水冲击特性并分析囊内气压、气囊壁、囊外液体压力三者之间的相互作用机理，以期为入水回收气囊参数的优化设计提供依据。

1 基本理论

1.1 CV法基本原理

基于理想气体均压模型，CV法认为气囊内压由理想气体状态方程决定，囊内各处压力相等[14]。CV法不拘泥于气囊内部流场细节，在气囊壁围成的气囊体积内，通过质量流量和温度两个与时间相关的参数描述气流变化。当不需要考虑气囊充气过程外形和流场变化时，CV法是一种简单高效的方法。例如本文中假设，环形密闭气囊内部为理想气体，且其热容恒定；气囊入水过程绝热，内部温度与压强均匀。根据以上假设，气囊的控制方程可以写为：

(1)

式中：p为气囊内压；V为气囊体积；n为囊内气体物质的量；R为理想气体常数；T为温度；k=Cp/CV为气体绝热指数，其中Cp和CV分别为定压和定容热容量；U为气囊内气体的内能。

1.2 LS-DYNA的流固耦合算法

采用LS-DYNA进行显式动力分析主要有Lagrange、Euler和ALE 3种算法[15]。其中Lagrange方法主要应用于固体的结构分析，这种方法描述的网格与结构是一体的，单元节点即为物质点，网格的变化与结构变形完全一致。Lagrange方法主要优点是能够精确描述结构边界的运动，但是在处理大变形问题时，会由于单元的严重畸变而导致计算终止。Euler方法以空间坐标为基础，空间网格与物质相分离，单元节点为空间点，物质可以在网格之间流动。这种方法的优点在于网格大小和空间位置不变，计算中具有恒定的计算精度，但难以准确描述物质边界，多用于流体分析中。ALE兼具以上两种方法的优点，首先通过Lagrange方法处理物质边界的运动变形，然后执行ALE时步计算，过程如下：(1) 保持变形后的物体边界条件，重新划分内部网格，网格的拓扑关系保持不变；(2) 将变形网格中的单元变量(密度、能量、应力张量等)和节点速度矢量输运到重分后的新网格中。目前，LS-DYNA主要是通过多物质ALE算法实现流体与结构的耦合，具体参考文献[15]，在此不加赘述。

2 数值模型建立

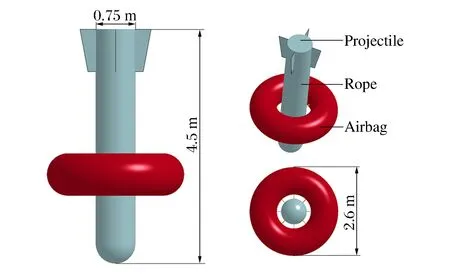
图1 气囊与弹体模型Fig.1 Airbag and projectile model

某实验弹上安装有回收气囊，在水面对其进行无动力回收，当弹体接近水面时，气囊迅速充气弹出，保证弹体落水后能够稳定并长时间漂浮，避免落水后击中水下装备，保障实验弹可靠回收。展开状态下的气囊与弹体模型如图1所示。弹体呈圆柱状，环形气囊展开后体积大约是2.8 m3，气囊壁厚大约是0.5 mm，气囊与弹体之间通过4根连接绳相连，连接绳直径为1.5 cm。模拟计算中将弹体设为刚体，其质量为2 523 kg，当以环形气囊中心为原点，以弹体轴线为z轴时，弹体相对于x、y、z轴的转动惯量Jxc、Jyc、Jzc分别为3 011、3 011、225 kg·m2。气囊壁和连接绳的材料参数见表1，其中ρ为密度，μ为泊松比，E为弹性模量。

表1 气囊和连接绳的材料参数Table 1 Material parameters of the airbag and corresponding rope

2.1 计算模型及边界条件

如图2所示，弹体和气囊在重力作用下，从水域上方以一定初速度坠入水中，计算中涉及到弹体、气囊、连接绳、水和空气的相互作用。运用LS-DYNA进行显式动力学分析时，流体采用 ALE算法，固体采用 Lagrange算法，固体和流体之间的相互作用通过流固耦合关键字定义，气囊与弹体之间通过自动单面接触关键字定义接触，连接绳与气囊之间通过生成节点刚性体的方式连接，与弹体之间采用共节点方式连接。有限元建模时，兼顾计算效率和精度，液体和空气采用 solid 164 单元划分成六面体网格，网格尺寸为0.2 m，气囊材料简化为各向同性的线弹性无弯矩薄膜材料，采用四边形薄膜单元划分网格，网格尺寸为0.1 m。连接绳采用柔性索单元划分网格，网格尺寸为0.1 m。弹体简化成刚性体，采用shell单元划分弹体外壳网格，并定义弹体质量特性。为模拟无限水域环境，取10 m×10 m×10 m水域范围，约束底部竖向自由度，其他水域边界及空气边界均设为无反射边界条件。最终生成的有限元模型如图3所示，一共划分了166 220个单元。

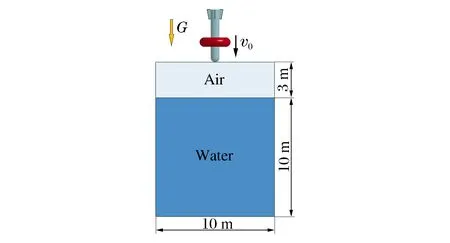
图2 计算模型示意Fig.2 Schematic diagram of calculation model

图3 有限元模型Fig.3 Finite element model

2.2 流体材料和状态方程

水和空气均采用MAT_NULL材料模型，通过Grüneisen状态方程描述，其压力为：

(2)

式中：p为压力；C为声速；S1、S2、S3为系数；γ0和E分别是Grüneisen常数和初始内能，均取为默认值零；a未来一阶体积修正系数；μ=ρ/ρ0-1，ρ和ρ0分别为当前密度和初始密度。水和空气参数设置如表2所示[16]，其中pc为截断压力，一般假定为负值；ν为材料动力黏度。

表2 水和空气参数Table 2 Parameters of water and air

3 仿真结果

3.1 流体压力静平衡

气囊入水过程中，随着深度增加，静水压力呈线性增加。为准确模拟自然环境中在重力作用下水域静压强环境(本文中水域压强、气囊内压等均以相对压强进行分析，即超出大气压的超压值)，在弹体和气囊入水之前，对水域压力进行静平衡处理。在LS-DYNA中用LOAD_BODY关键字模拟重力，结合INITIAL_ALE_HYDROSTATIC关键字对静水压强进行初始化。如图4所示，流体压强在0.05 s以内即达到平衡状态，平衡状态符合静水压强公式[17]：

(3)

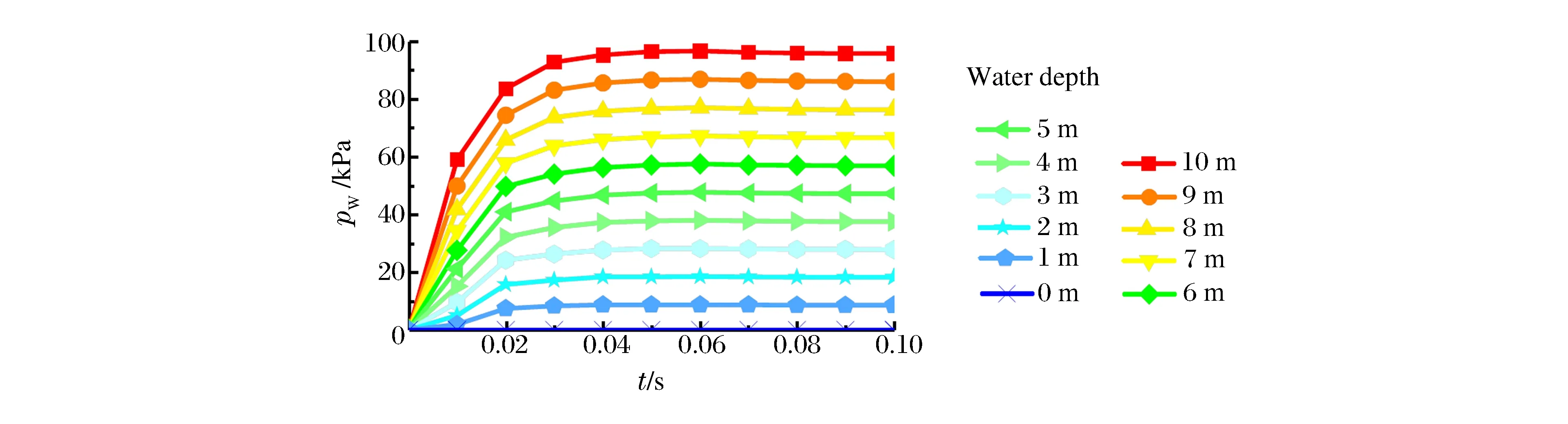
图4 流体压力静平衡状态Fig.4 Static equilibrium state of fluid pressure

3.2 气囊及弹体的入水过程

气囊和弹体的入水过程主要分为弹体砰水、气囊着水、入水减速、水中悬停、缓慢上浮、上浮出水、水面漂浮7个阶段。气囊的缓冲作用主要体现在气囊着水阶段；入水减速阶段主要受流体黏滞阻力、浮力和重力影响；当弹体到达最低点附近，在一段时间内将处于悬停状态(此阶段速度非常小，可以认为是静止状态)；随后，浮力作用使弹体和气囊开始缓慢上浮，并最终稳定漂浮在水面。各阶段的特征受初始条件影响较大，取气囊初始囊压为50 kPa，弹体初始速度为50 m/s，数值模拟弹体从距离水面3 m处垂直入射或从距离水面垂直高度为2.14 m处斜入射(弹体轴线与水面夹角为45°)的入水过程。

3.2.1弹体垂直入射

如图5所示，在0.06 s时刻，弹体头部接触水面，此时为弹体砰水阶段。0.09 s时，气囊接触水面，在冲击挤压及水压作用下，气囊迅速压缩，起到减速与缓冲作用。由于入水速度较快，弹体和气囊周围形成较大范围的空泡现象[13,18-19]。入水之后，在浮力和流体黏滞阻力作用下，气囊和弹体持续减速，直到0.81 s，速度减为零，气囊和弹体在水中基本处于悬停状态；此时周围的空泡逐渐闭合，水面溅起较高的水花。从2.81 s开始，气囊和弹体缓慢加速上浮，上浮最大速度小于2 m/s，最终在6.72 s时浮出并漂浮在水面，整个过程弹体始终保持直立姿态。图5中弹体周围空泡的生成、发展和闭合过程及形态与文献[18]和文献[19]中弹体垂直入水的实验照片基本一致，但图5中弹体带有气囊，形成的空泡范围更大。图6和图7分别为入水过程中弹体头部节点的速度和位移时程曲线，反映出各阶段的速度和位移变化特征。由图6～7可知：弹体从入水到浮出水面历时约为6.7 s，最大入水深度为6.47 m(垂直入射时，零时刻弹体距离水面高度为3 m)。

3.2.2弹体45°角斜入射

“春施千担肥，秋收万石粮”。“供”的是一种分担，“供”的是一份心意。黑龙江销售深处在农业大省的区域，深知肩负的责任和使命，虽然全年“春耕、秋收”保供时间长，黑龙江销售人早已将保供当成常态化的工作来做实、做细。

与图5对应，斜入射时弹体和气囊入水的全过程如图8所示。0.06 s弹体砰水；0.09 s气囊着水；0.14 s气囊完全入水；随后一直到0.56 s为入水减速阶段；0.56 ～1.25 s为水中悬停阶段，此时弹体头部速度极小，主要是尾部在运动，弹体由倾斜转变成直立姿态；1.25 s时刻弹体和气囊开始上浮；2.25 s完全浮出水面。

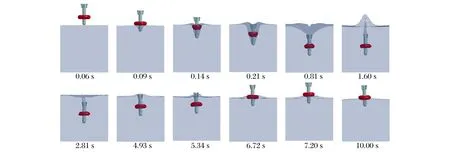
图5 垂直入射全过程Fig.5 Processes of vertical incidence

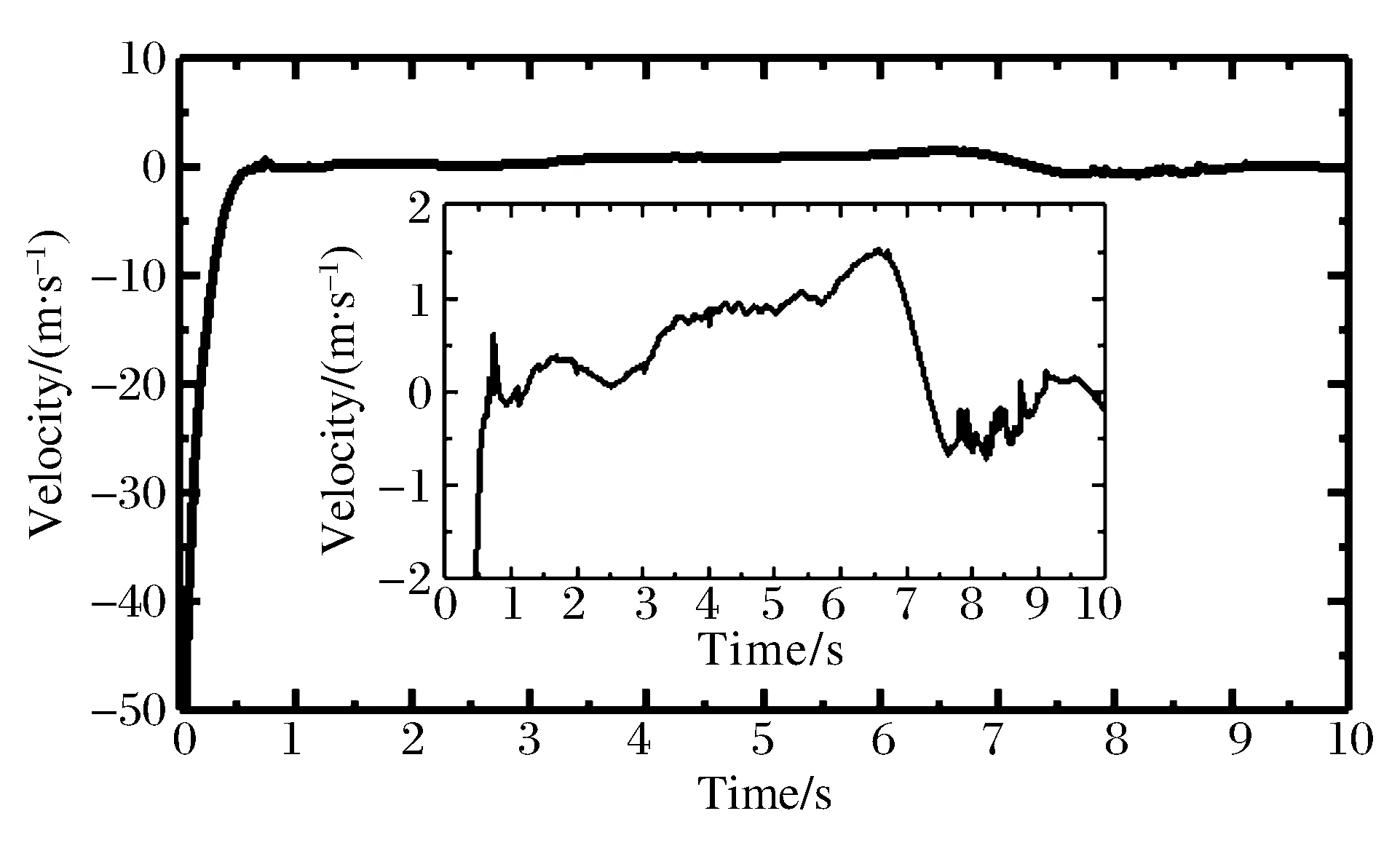
图6 弹体头部节点的竖向速度时程曲线Fig.6 Vertical velocity history curve of projectile’s head node

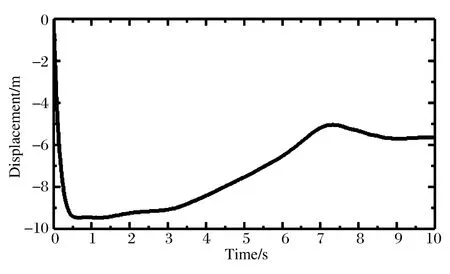
图7 弹体头部节点的竖向位移时程曲线Fig.7 Vertical displacement history curve of projectile’s head node

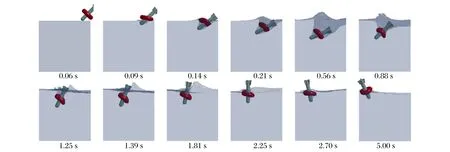
图8 斜入射全过程Fig.8 Process of oblique incidence

斜入射时弹体在水中的姿态与垂直入射有较大差异，以弹体头部节点为基点，图9和图10分别是斜入水过程中弹体的平动速度和平动位移时程曲线，图11和图12分别是弹体的角速度和角位移(顺时针为正，逆时针为负)时程曲线。入水后弹体角速度迅速增大到正向峰值，弹体轴线与水平方向的夹角逐渐减小，这是由于入水减速后弹体头部和尾部速度不一致导致的：头部所受阻力较大，并且受到气囊和连接绳的拉力，所以竖向速度衰减较快，而空泡主要靠近尾部，所以尾部所受阻力较小。这样，入水之后弹体头部竖向速度将小于尾部，弹体将发生顺时针旋转。直到到达最低点，气囊开始上浮，在连接绳拉力作用下，弹体角速度逐渐由正转为负，弹体调整到直立状态，并上浮出水，上浮速度小于1 m/s，最终弹体和气囊一起在水面漂浮。从入水到浮出水面历时约2.3 s，最大入水深度为3.67 m(斜入射时，零时刻弹体距离水面高度垂直高度为2.14 m)。

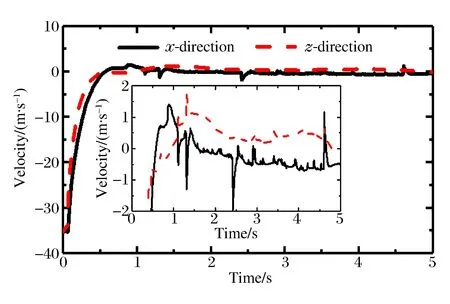
图9 弹体头部节点的竖向和水平速度时程曲线Fig.9 Vertical and horizontal velocity history curves of projectile’s head node

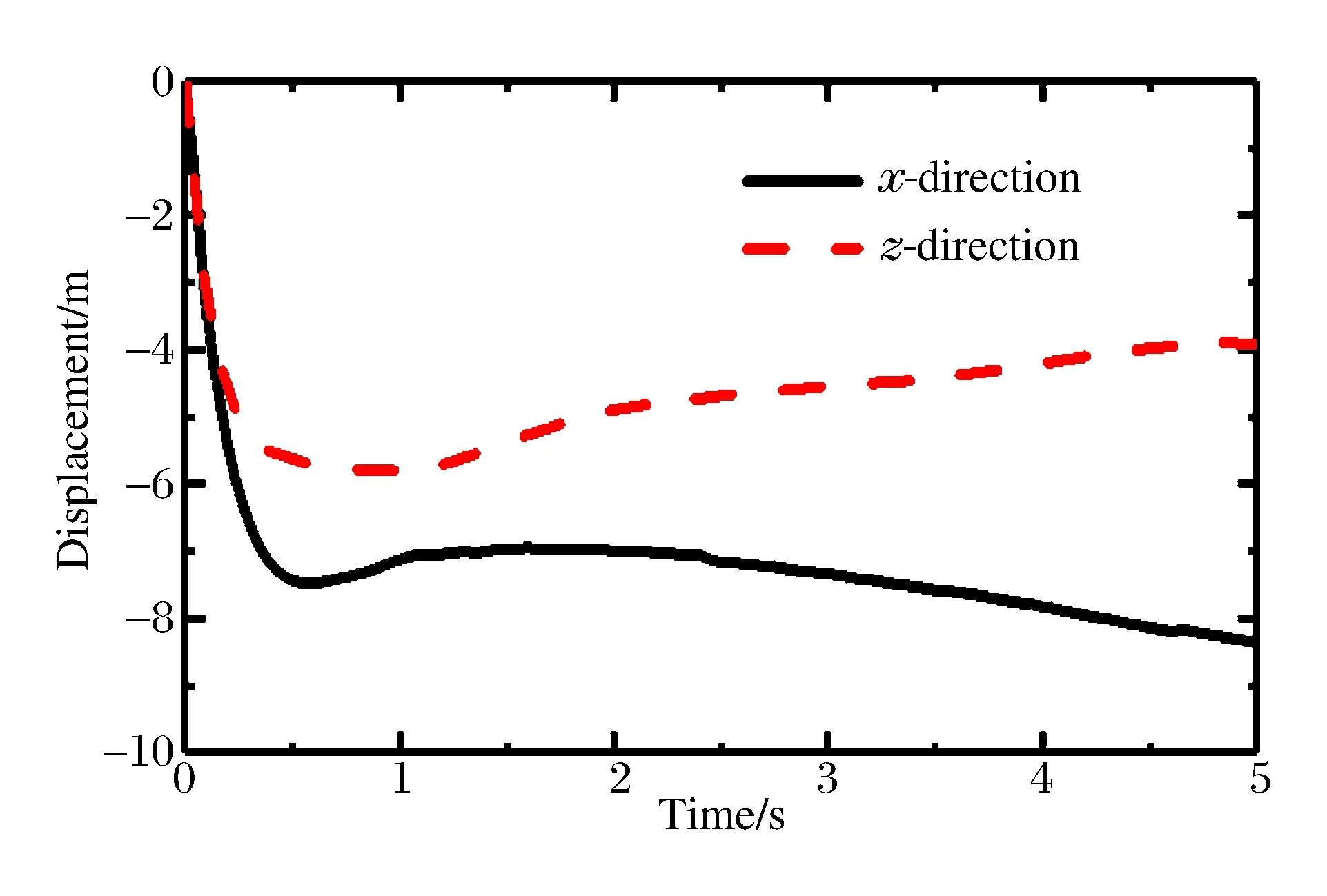
图10 弹体头部节点的竖向和水平位移时程曲线Fig.10 Vertical and horizontal displacement history curves of projectile’s head node

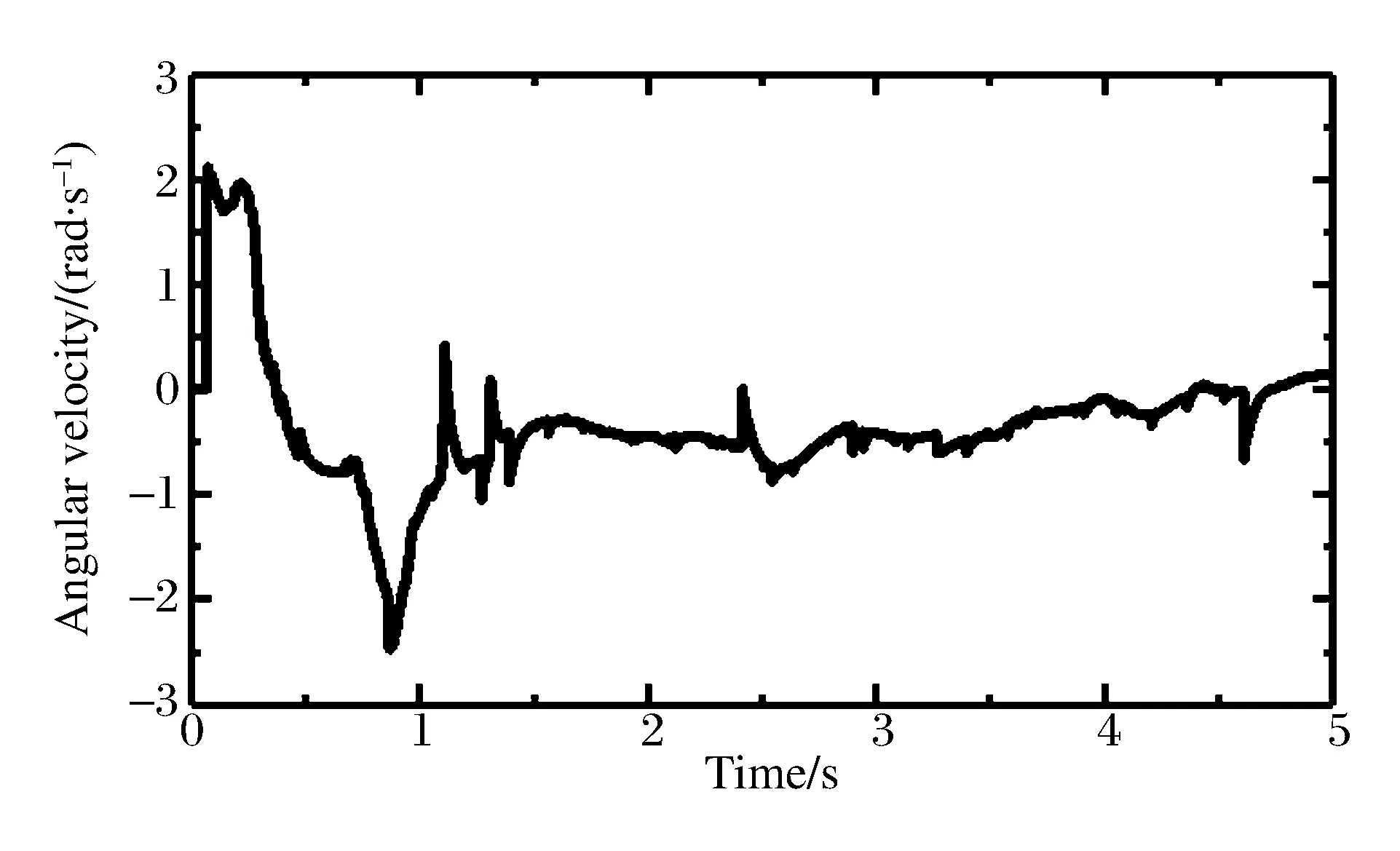
图11 弹体角速度时程曲线Fig.11 Angular velocity history curve of projectile

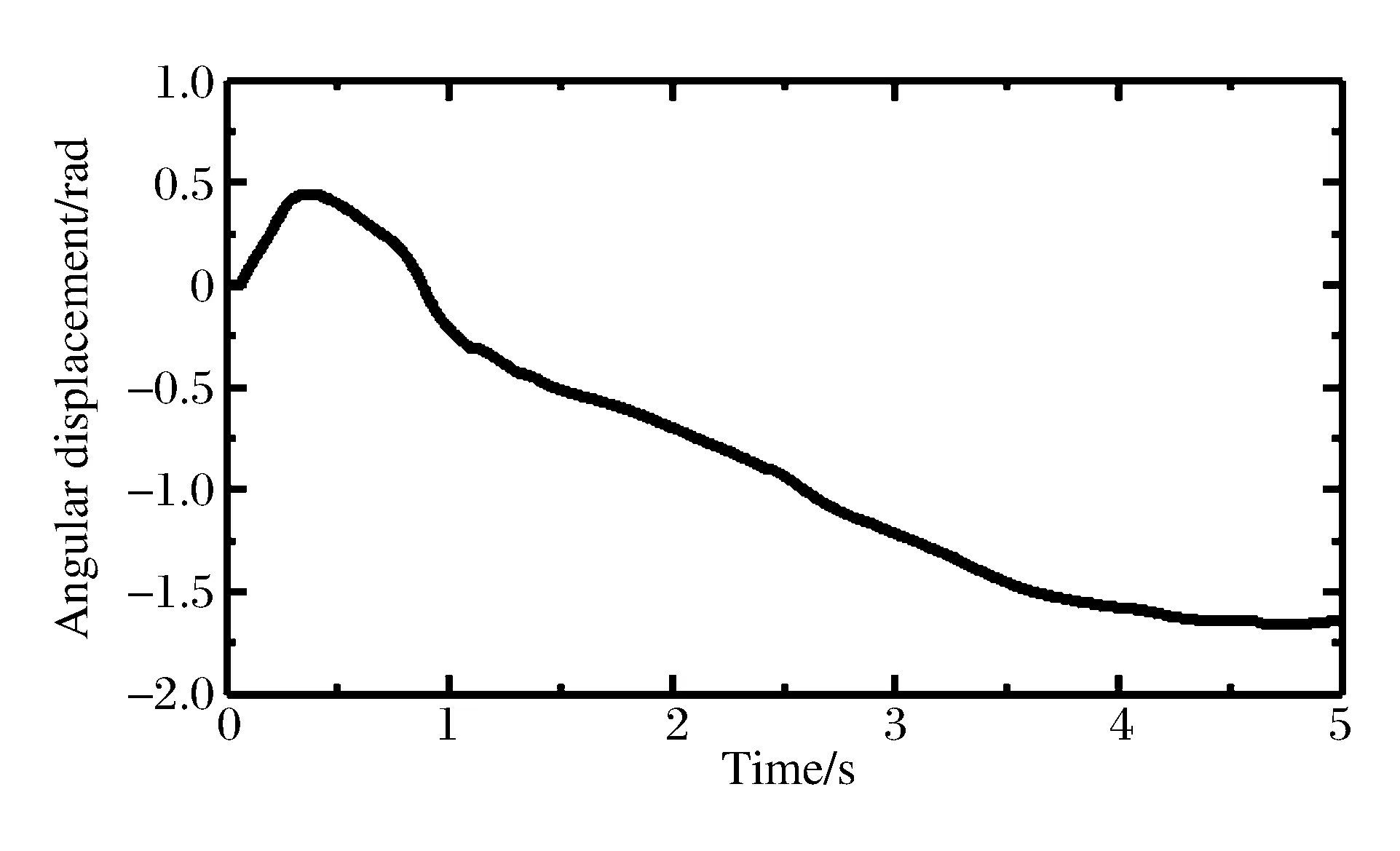
图12 弹体角位移时程曲线Fig.12 Angular displacement curve of projectile

3.3 流体与气囊的相互作用

在着陆过程中，气囊着陆缓冲系统会发生多次弹跳，受摩擦力、气囊结构阻尼和内流阻尼的影响，弹跳速度会逐步降低，着陆动能在与地面碰撞过程中逐步衰减[20]。因此，着陆过程中气囊内压会出现多次波动峰值，并且峰值大小逐步衰减。气囊入水过程与着陆过程有明显差异：(1) 气囊着水阶段是气囊与流体碰撞的流固耦合冲击问题，该过程中流体本身对碰撞有一定的缓冲作用，和气囊与地面碰撞不同，不会出现弹跳现象；(2) 流体的黏滞阻力与速度v呈正比，随着弹体和气囊在水中运动速度的减小，阻力逐渐减小；(3) 随着入水深度h的增加，流体对气囊的压力逐渐增大；(4) 弹体和气囊之间连接绳拉力T也是影响囊压的重要因素。因此，在入水后到上浮过程中，气囊内压可用以下函数表示：

(4)

式中：p0为气囊初始内压，h、v、Trope均是与时间相关的函数，分别表示入水深度、运动速度、连接绳拉力，ρ、μ分别为流体密度和黏滞系数。

图13为气囊内压的变化曲线。初始囊压为50 kPa，弹体以50 m/s的初始速度从水面上方入射，分为垂直入射和45°斜入射两种情况。在气囊着水阶段，气囊与水面猛烈碰撞，气囊急剧变形，囊压迅速升高到峰值，囊压变化曲线与文献[21]一致。随后，由于入水速度较大，气囊和弹体排水形成空泡，水对气囊的压力减小，气囊内压迅速减小。随着空泡的闭合，水猛烈撞击气囊，气囊内压再次迅速上升到峰值，然后随着运动速度的衰减而缓慢衰减。可以看到，垂直入射时，在1.5～3.0 s时间段内，气囊内压基本稳定在约68 kPa，此时间段对应于气囊和弹体到达最低点，处于悬停阶段。此后，随着气囊上浮，静水压力减小，气囊内压逐渐减小。无论是斜入射还是垂直入射，浮出水面后，漂浮状态下，气囊的内压都稳定在约52.5 kPa。

图14为流体对气囊的作用力合力的时程曲线，垂直入射时，合力主要沿z方向，另外两个方向基本为零；而斜入射主时合力主要沿z方向和x方向，且z方向合力略大于x方向。结合弹体的速度变化进行分析可以发现：流体合力峰值出现的区间正是气囊着水和水中减速阶段，并且与囊压峰值出现的时间段一致；当初始速度衰减到零之后，流体对气囊的作用合力主要是向上的浮力。

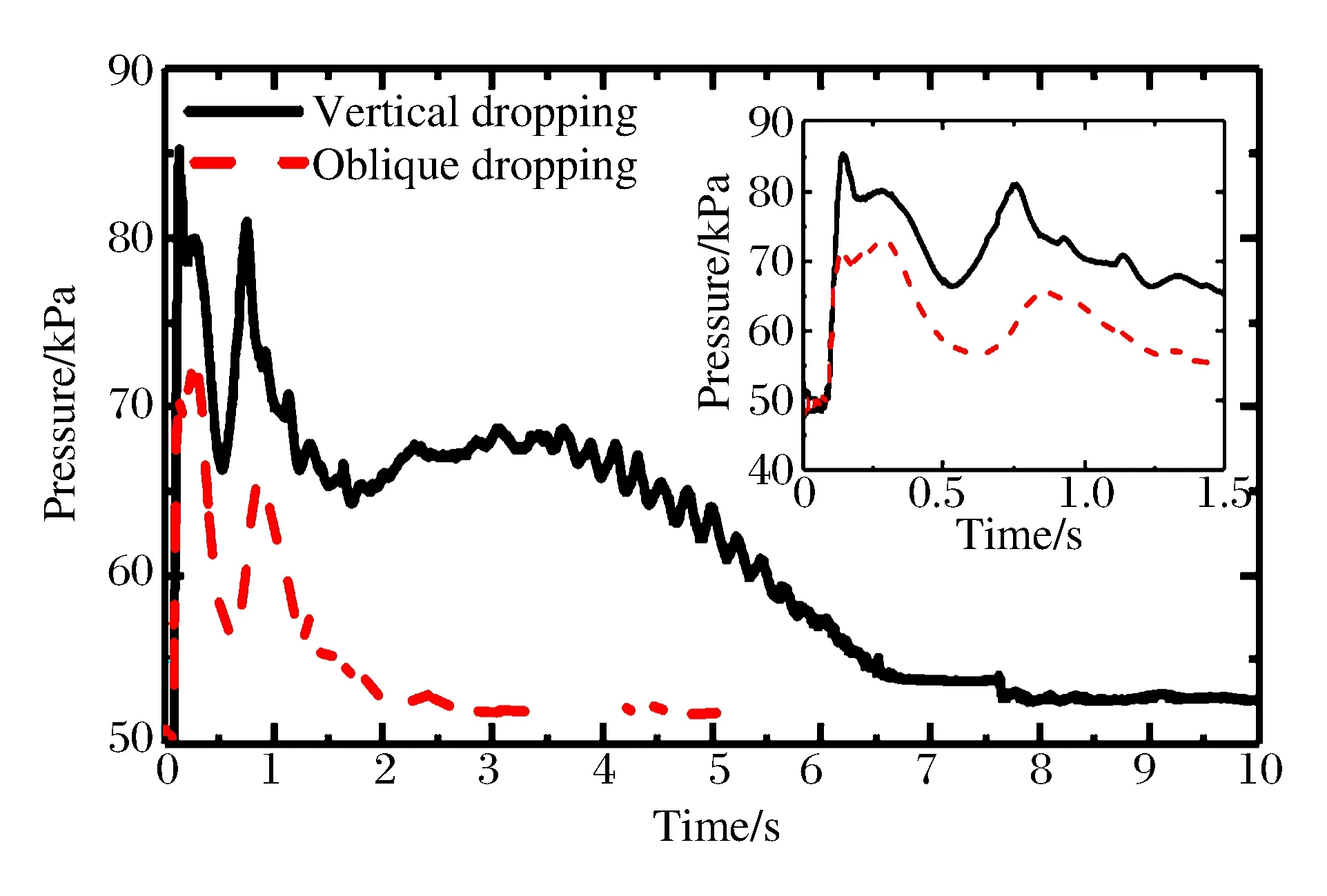
图13 气囊内压变化曲线Fig.13 Internal pressure change curve of airbag

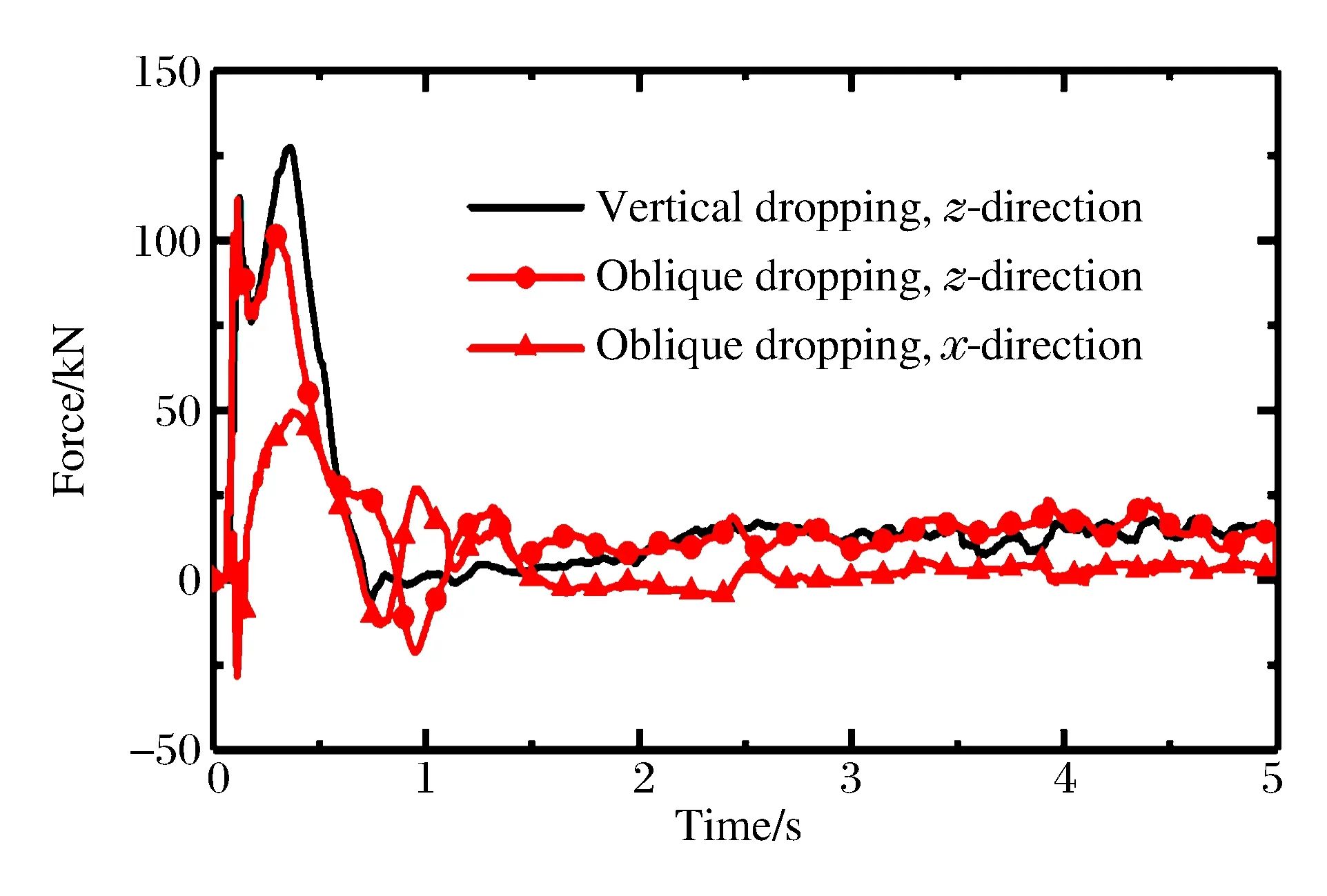
图14 流体对气囊的作用力合力时程曲线Fig.14 Time history curve of fluid force on airbag

由以上分析可知，入射速度对气囊压力峰值的大小有很大影响。设气囊初始内压为50 kPa，弹体以不同初速度垂直入射到水中，在此条件下计算得到气囊内压峰值与初始速度之间的关系曲线，如图15所示。可以看出：初始速度越大，囊压峰值越高，即气囊受水的冲击力越大。

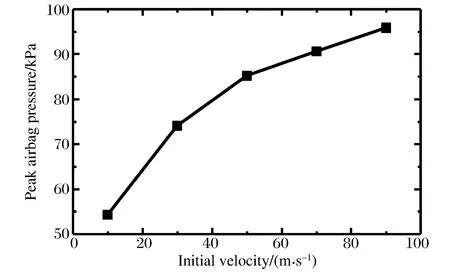
图15 囊压峰值与初始速度的关系曲线Fig.15 Relationship between peak value of airbag internal pressure and initial velocity

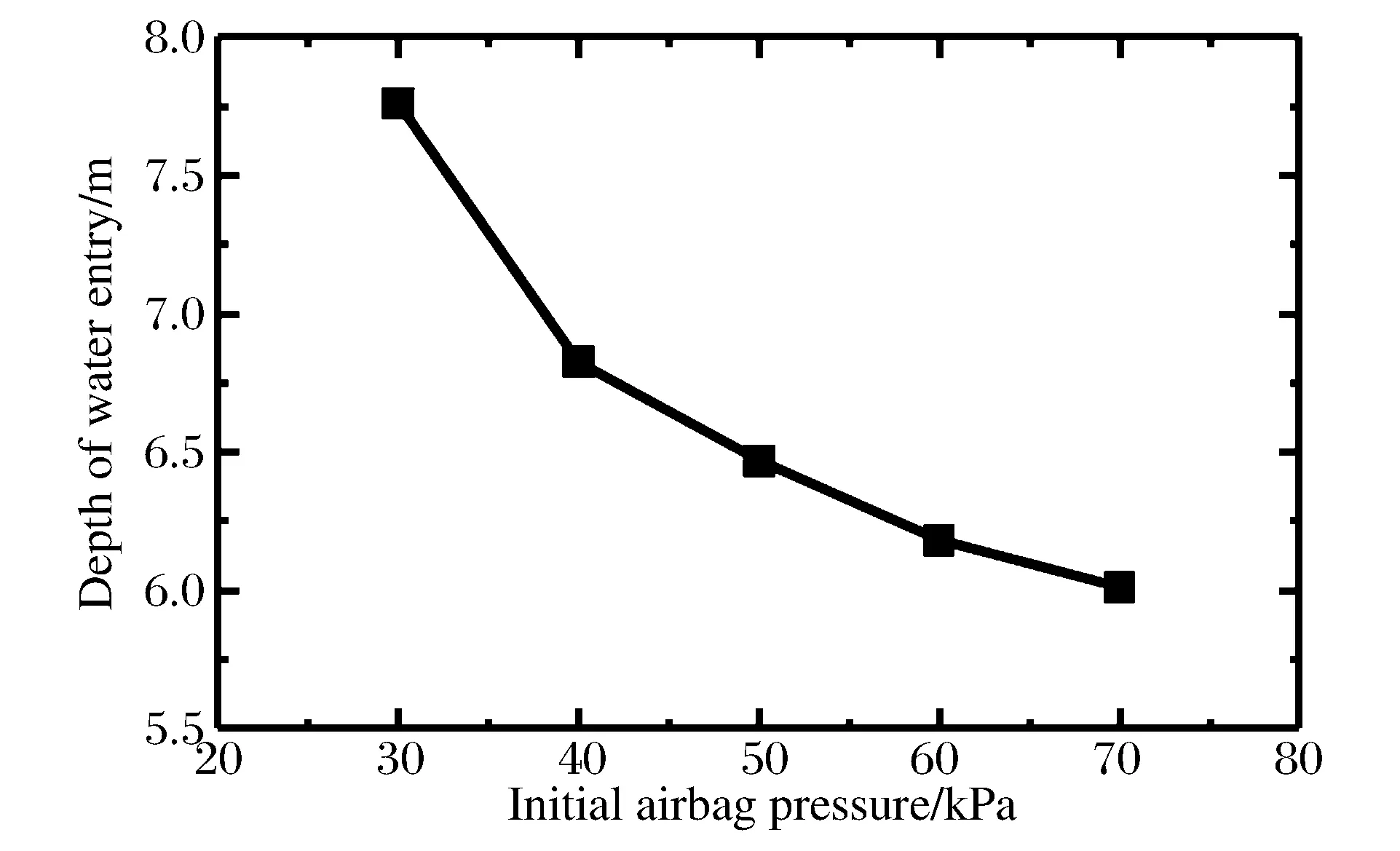
图16 入水深度与初始囊压的关系曲线Fig.16 Relationship between water entry depth and initial airbag internal pressure

3.4 气囊的缓冲作用

气囊内压是进行缓冲气囊优化设计的重要参数。在软着陆气囊设计中，囊压太低容易引起气囊变形过大，从而导致“硬着陆”而损坏结构；气压太高又会导致缓冲加速度上升，缓冲效果不佳[22]。在气囊入水问题中，随着入水深度的增加，气囊内压在流体压力作用下会升高。根据CV法原理，密闭气囊体积与内压呈反比，因此，若气囊初始囊压过低，入水压缩后气囊体积偏小，所产生的浮力和阻力不够，则会导致入水过深无法短时间内浮出水面，甚至沉入水底。

图16为弹体以50 m/s的速度垂直入水时入水深度与初始囊压之间的关系曲线。可以看出，入水深度随着囊压的降低而增大。充气完成后，气囊体积约为2.8 m3，弹体本身的排水体积约为1.9 m3，根据浮力计算公式[17]，所能产生的浮力大于弹体及结构重力。但是当气囊囊压过低时，随着入水深度的增大，气囊体积持续被压缩，最终所能产生的浮力将不足以抵消重力，气囊将无法上浮甚至沉入水底。在压力为20～30 kPa区间内按照二分法选取囊压进行计算，可以确定气囊的临界压力大约为23.75 kPa，低于此压力，弹体将沉没。

图17为初始囊压与弹体速度减到零所耗时间的关系曲线。可以看出：初始囊压越高，减速时间越短，减速效果越好。但是囊压的设计值并不是越高越好。一方面，囊压过高可能导致回收过程中气囊破裂，影响整个弹体回收过程的安全性与可靠性；另一方面，气囊与弹体之间连接绳的拉力峰值随着囊压的升高而增大，即囊压越高，连接绳对弹体的冲击力越大，这样极有可能导致回收过程中弹体外壳被拉坏，影响回收效果，如图18所示。因此，在进行入水回收气囊参数设计时，有必要根据实际情况综合考虑缓冲效果、减速效果以及气囊安全性等因素。

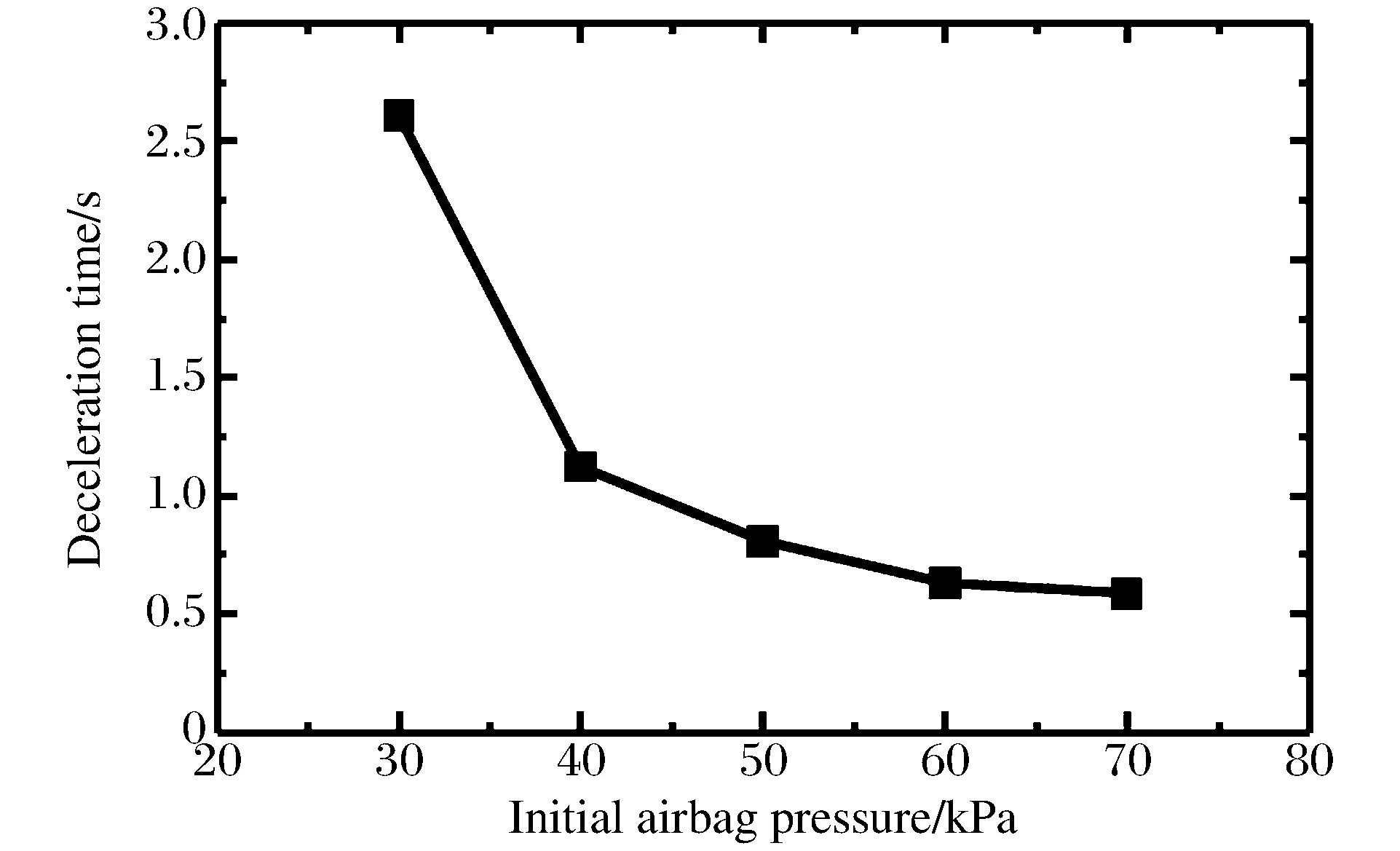
图17 减速时间与初始囊压的关系曲线Fig.17 Relationship between deceleration time and initial airbag internal pressure

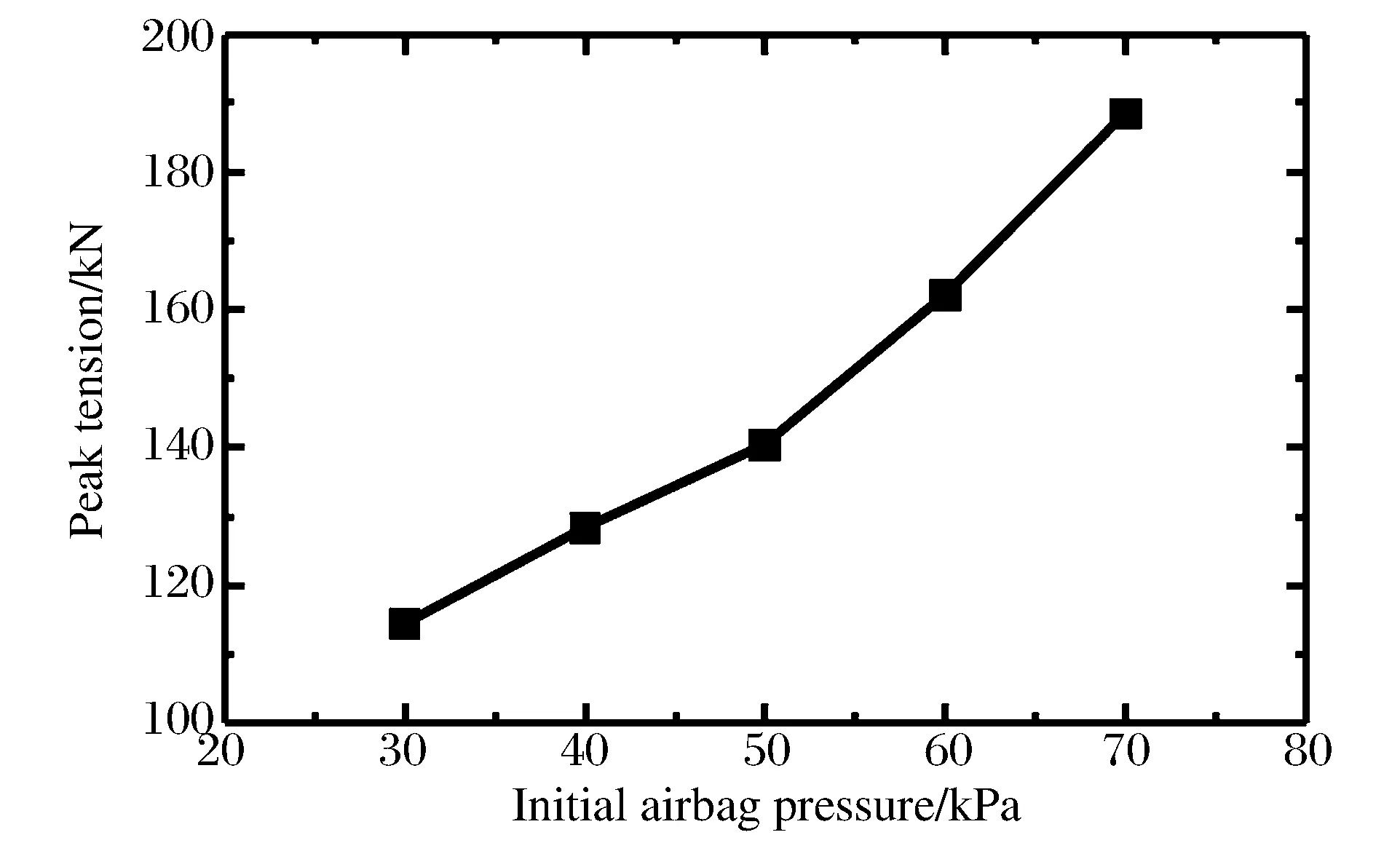
图18 连接绳拉力峰值与初始囊压的关系曲线Fig.18 Relationship between peak tension of connecting rope and initial airbag internal pressure

4 结 论

基于LS-DYNA，运用CV法模拟环形密闭气囊，结合流固耦合算法，模拟了某弹体及附带环形密闭气囊在展开状态下的入水过程，分析了多种工况下气囊和弹体入水姿态，探讨了影响气囊和弹体入水回收效果的多种因素，可得到以下结论。

(1) 气囊和弹体的入水过程分为弹体砰水、气囊着水、入水减速、水中悬停、缓慢上浮、上浮出水、水面漂浮7个阶段。弹体垂直入水后能始终保持直立姿态；斜入水初期，弹体轴线与水平方向夹角会有所减小，但随着运动速度的衰减，弹体在悬停阶段开始逐渐调整姿态，并在上浮阶段中逐渐转变成直立姿态，浮出水面后弹体能保持直立姿态漂浮在水面。

(2) 气囊入水过程中囊压的变化主要受入水深度、运动速度、连接绳拉力等因素影响。囊压峰值出现在气囊着水阶段，此时气囊与水面猛烈碰撞，水对气囊的冲击力较大。在上浮阶段随着入水深度减小，气囊内压也逐渐减小。另外，入水冲击过程中气囊内压峰值随着入水速度的增大而升高。

(3) 弹体入水深度随着气囊初始内压的降低而增大。初始内压过低可能导致气囊减速时间过长，或气囊入水后产生的浮力不足以抵消弹体重力而沉入水底。气囊内压越高，入水冲击过程中连接绳对弹体的拉力峰值越大。当囊压过高时，连接绳可能会拉坏弹体外壳，从而影响回收效果。因此，在进行入水回收气囊参数设计时，需要综合考虑缓冲效果、减速效果及气囊安全性等因素。