低值可回收物管理机制的演化博弈分析

张爽，孙绍荣，马慧民

（1. 上海理工大学 管理学院 上海 200093；2. 上海电机学院 商学院 上海 201306）

再生资源是城市固体废弃物的重要组成部分，回收利用就成为资源，不能有效回收利用则成为垃圾[1]。比如生活中的废玻璃，欧洲的回收率高达90%，而在我国，85%都被混在垃圾中丢弃。我国再生资源利用率偏低，尤其废玻璃、废纺织物、废包装纸等低值可回收物被大量废弃，既加剧了垃圾围城趋势，又造成了环境污染[2]。我国环保部发布的《2017 年全国大、中城市固体废物污染环境防治年报》[3]显示，2016年，我国214个大、中城市生活垃圾产生量18 850.5万t，其中上海年生活垃圾产生量最大，达879.9万t，同比增长11.4%，大中城市垃圾减量化形势依然严峻。

提高低值可回收物的资源化利用率可以防止其混入生活垃圾，从源头上减少生活垃圾产生量，降低政府的垃圾处理成本，减少环境污染。然而由于低值可回收物回收成本高、利润薄，单靠市场机制难以调动企业对其进行回收处理，因此，政府需要进一步加强政策支持和制度创新[4]。国外采取诸如押金制等政策措施[5-6]来提高可回收物的再循环利用。国内，广州2015年出台了《广州市购买低值物回收处理服务管理试行办法》，通过政府购买服务的方式补贴低值可回收物处理，取得了不错的效果[7]。南京于2017年出台了《南京市低价值可回收物回收处理暂行办法》，该办法于2017年11月20日开始执行，成为继广州之后，又一个出台有关低值可回收物管理规定的城市。

近年来，国内在垃圾管理研究方面取得了一定的成果，但这些成果主要集中在垃圾分类管理方面[8-14]，低值可回收物管理方面的研究成果较少，且主要以定性分析为主[1,4,7]。演化博弈论[15]作为一种定量研究方法在经济管理领域[16-20]已经有了广泛应用，但在垃圾管理领域目前应用较少，仅在高校垃圾分类回收监管机制[21]和城市垃圾分类回收逆向物流监管机制[22]方面有一些成果，再生资源回收管理方面还鲜有研究。

鉴于此，本文在现有研究成果基础上，根据演化博弈的基本理论，选择有限理性的地方政府、企业这两个低值可回收物资源化利用涉及的最主要利益相关者进行演化博弈分析，同时运用Matlab对演化过程进行仿真，以弥补国内在低值可回收物管理机制领域研究的不足，揭示低值可回收物资源化处理中利益主体决策行为的演化特征，试图提出相应的政策措施，为政府有效进行垃圾减量提供理论上的支持。

1 演化博弈模型假设与建立

模型构建涉及两类参与主体：政府、企业。政府的行为策略集为（鼓励，不鼓励），企业的行为策略集为（回收，不回收）。

假设1 由于低值可回收物的回收成本高、利润薄，单靠市场机制难以调动企业积极性，需要政府进一步加强政策支持和制度创新。设政府对低值可回收物的回收企业予以一定的补贴， 鼓励企业回收低值可回收物并进行资源化利用；通过回收企业对低值可回收物回收以及资源化利用，有效进行垃圾减量，减少直接填埋或焚烧的垃圾量，一定程度上改善生活环境，设地方政府得到的环境正效益为。

假设2 地方政府采取鼓励政策，将垃圾处理与再生资源利用“两网融合”，提高资源回收利用率，有效促进污染减排。设地方政府采取鼓励政策并进行两网融合时，低值可回收物的收运成本为C1，处理成本为C3；地方政府采取不鼓励政策，将低值可回收物与生活垃圾混合运输时，低值可回收物的收运成本为C2，处理成本为C4。

假设3 地方政府采取积极鼓励政策，促使企业对低值可回收物的回收，使得生活垃圾减量效果明显，此时上级政府给予的奖励和在社会公众间享有公众认可或社会声望之和为；同时，如果地方政府的积极主动作为，虽没有促成回收企业的回收行为，但在社会公众间也会享有一定的公众认可或社会声望，该值记为S。

假设4 企业将低值可回收物资源化利用获得的经济收益记为Q。企业对低值可回收物回收的成本既包含收运成本，也包含资源化处理成本。那么在地方政府采取不鼓励政策下，企业将低值可回收物资源化利用的全部成本记为R1；在地方政府采取积极鼓励政策下，企业将低值可回收物资源化利用的全部成本记为R2。可知R1＞R2。

假设5 假设政府群体中选择鼓励策略的比例为x，选择不鼓励策略的比例为（1−x）；企业群体中选择回收策略的比例为y，选择不回收策略的比例为（1−y）。

通过以上的概念界定和模型假设，可以构建政府、企业博弈双方的收益矩阵如图1所示。

图1 博弈双方的收益矩阵Fig.1 Revenue matrix between government and enterprises

2 演化博弈均衡分析

2.1 演化博弈的复制动态方程

设政府选择“ 鼓励”和“不鼓励”策略的期望收益为E1和E2，政府混合策略的平均期望收益为。

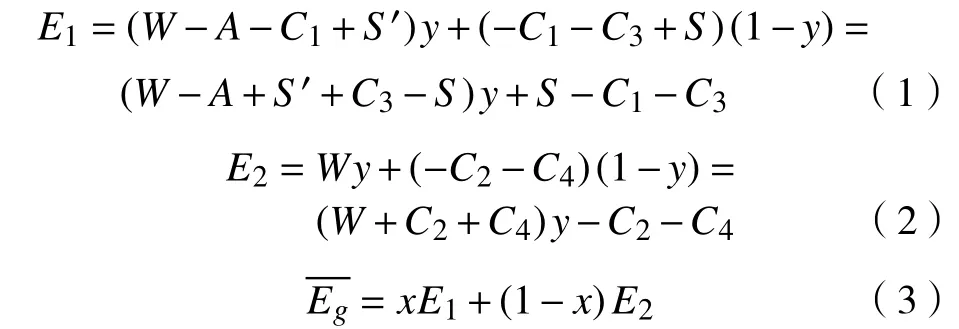
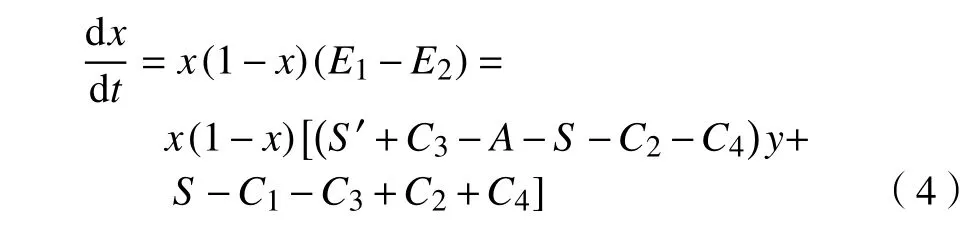
设企业选择“回收”和“不回收”策略的期望收益为E3和E4，企业混合策略的平均期望收益为 。

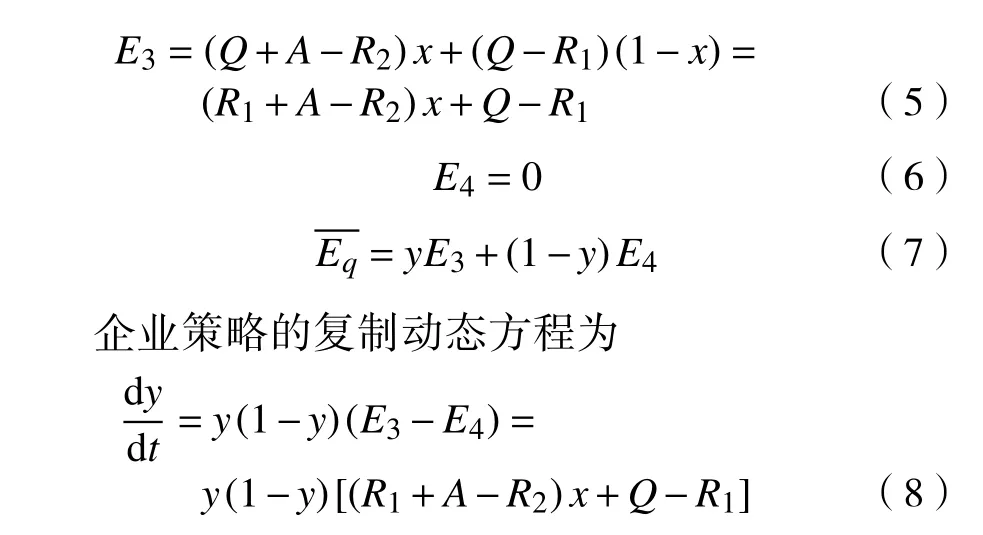
2.2 政府和企业策略的演化博弈均衡分析

联合复制动态方程式（4）和式（8），得到一个二维动力系统，得到如下联立方程组：

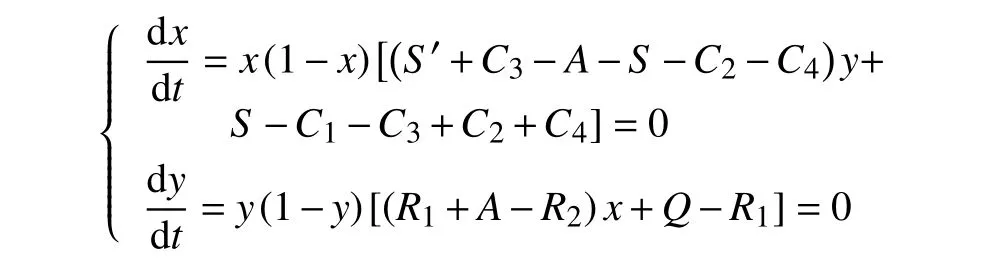
由如上方程组可求得系统5个平衡点，分别为（0，0），（0，1），（1，0），（1，1）和（m，n），时成立。

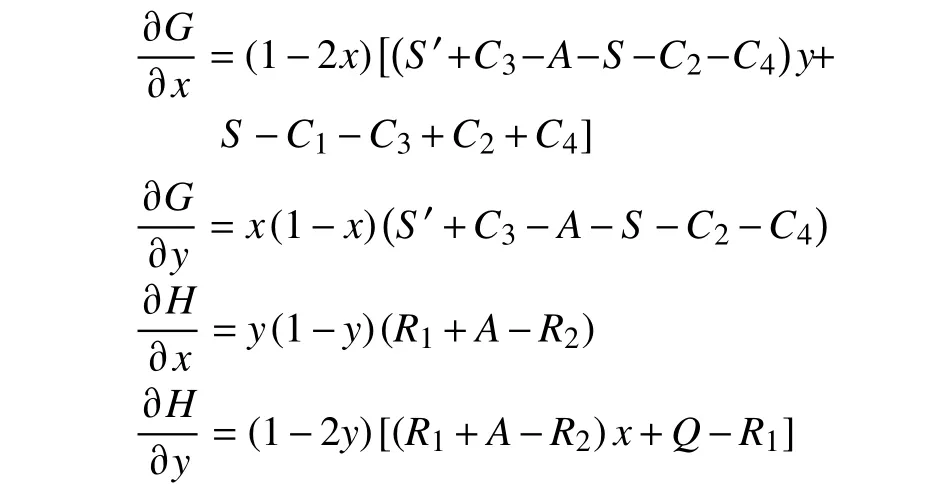
表1 平衡点对应的雅可比矩阵行列式和迹的表达式Tab.1 Jacobian matrix’s determinant and trac corresponding to equilibrium points

经上述计算易知，平衡点（m，n）处迹的值为0，不满足tr J＜0，因此该局部均衡点肯定不是演化稳定策略（evolutionarily stable strategy，ESS）。故以下将分析4个系统平衡点成为ESS的可能性。S′−A−C1＞0Q+A−R2＞0 S−C1−C3+C2+C4＜0Q−R1＜0

结论1 若满足 ， ，且不满足 ， ，则系统的演化稳定策略为（1，1）。

证明 根据演化博弈论的性质可知，上述4个平衡点的局部稳定性可由该系统相应的雅可比矩阵行列式和迹的值来判定。当且仅当det J＞0，且tr J＜0时，该均衡点具有稳定性。

下面分3种情况进行讨论。S′−A−C1＞0Q+A−R2＞0S−C1−C3+C2+C4＞0Q−R1＞0

情况1 当 ， ，， 时，平衡点分析如表2所示。此时系统存在唯一演化稳定策略（1，1），（0，1）和（1，0）为系统的鞍点，（0，0）为不稳定点。这种情况下，政府的行为最终趋向于选择鼓励策略，企业最终趋向于选择回收策略。

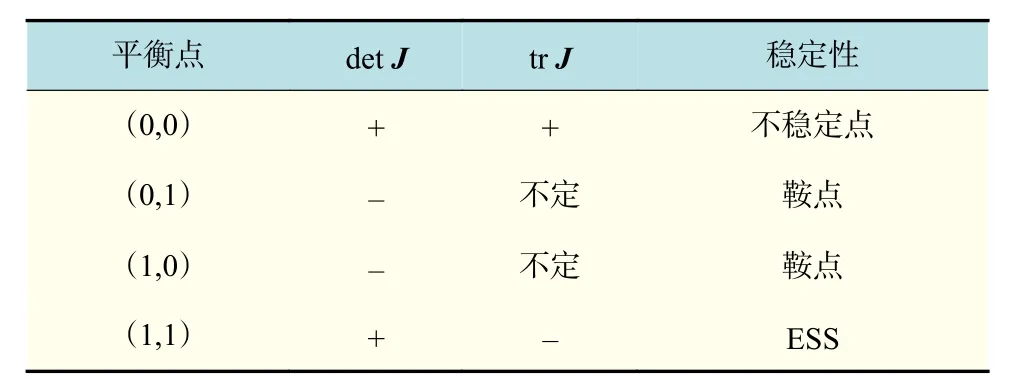
表2 结论1情况1的平衡点局部稳定性Tab.2 Local stability of the equilibrium point in case 1 of conclusion 1

情况2 当 S′−A−C1＞0， Q +A−R2＞0， S−C1−C3+C2+C4＞0，Q−R1＜0时，平衡点分析如表 3所示。此时系统存在（0，0）和（1，0）两个鞍点，（0，1）一个不稳定点，以及唯一的演化稳定策略（1，1）。 S′−A−C1＞0Q+A−R2＞0S−C1−C3+C2+C4＜0Q−R1＞0

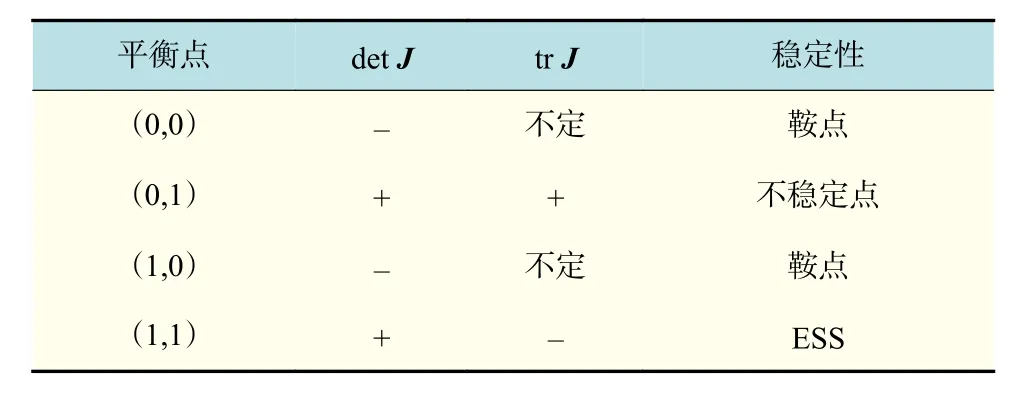
表3 结论1情况2的平衡点局部稳定性Tab.3 Local stability of the equilibrium point in case 2 of conclusion 1

情况3 当 ， ， ，

时，平衡点分析如表 4所示。此时系统存在（0，0）和（0，1）两个鞍点，（1，0）一个不稳定点，系统的演化稳定策略仍为（1，1）。

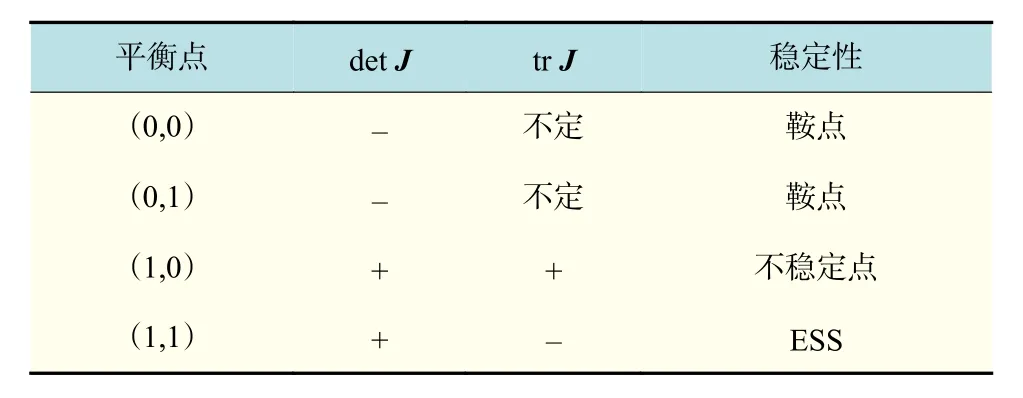
表4 结论1情况3的平衡点局部稳定性Tab.4 Local stability of the equilibrium point in case 3 of conclusion 1

通过以上3种不同情况的分析，易知结论1成立。结论1说明：当地方政府的积极作为得到的上级政府奖励以及享有公众认可或社会声望之和，大于地方政府对回收企业的补贴和低值可回收物的收运成本两者之和；企业资源化利用的经济收益和地方政府给予的补贴两者之和，大于地方政府采取鼓励政策下企业资源化利用的全部成本；且不同时满足地方政府的积极作为虽未促成企业的回收行为，但仍得到的公众认可或社会声望，与地方政府不鼓励政策下低值可回收物的收运成本、处理成本三者之和，小于地方政府采取鼓励政策时低值可回收物的收运成本和处理成本两者之和；也不满足企业资源化利用的经济收益小于地方政府采取不鼓励政策下企业资源化利用的全部成本时，企业的行为选择将全部趋向于回收，政府的行为选择将趋向于鼓励。

结论2 若满足 S −C1−C3+C2+C4＜0， Q−R1＜0且不满足 S′−A−C1＞0， Q +A−R2＞0，则系统的演化稳定策略为（0，0）。

证明 同理，分3种情况讨论：

情况1 当 S −C1−C3+C2+C4＜0， Q −R1＜0，S′−A−C1＜0，Q+A−R2＜0时，平衡点分析如表5所示。此时系统存在唯一演化稳定策略（0，0），（0，1）和（1，0）为系统的鞍点，（1，1）为不稳定点。这种情况下，政府的行为选择将最终演化为不鼓励策略，企业的行为选择将最终演化为不回收策略。S−C1−C3+C2+C4＜0Q−R1＜0 S′−A−C1＜0Q+A−R2＞0

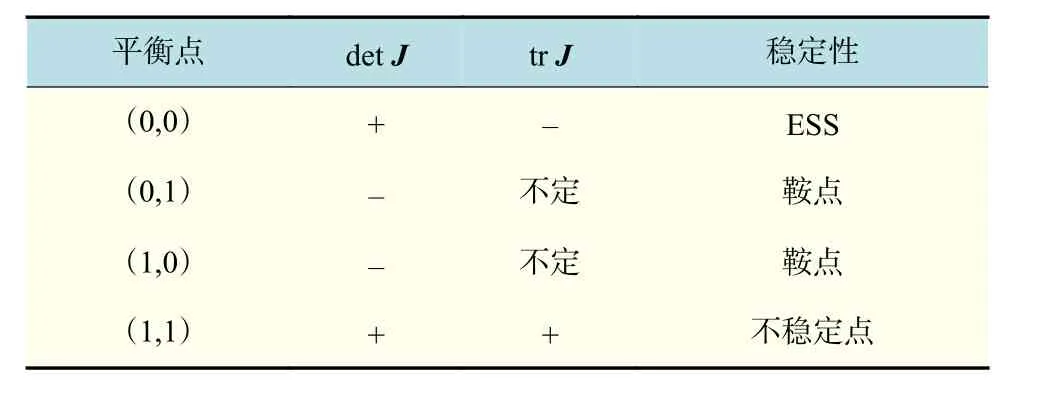
表5 结论2情况1的平衡点局部稳定性Tab.5 Local stability of the equilibrium point in case 1 of conclusion 2

情况2 当 ， ，，时，平衡点分析如表6所示。此时系统存在唯一演化稳定策略（0，0），（0，1）和（1，1）为系统的鞍点，（1，0）为不稳定点。这种情况下，政府的行为选择将最终演化为不鼓励策略，企业的行为选择将最终演化为不回收策略。

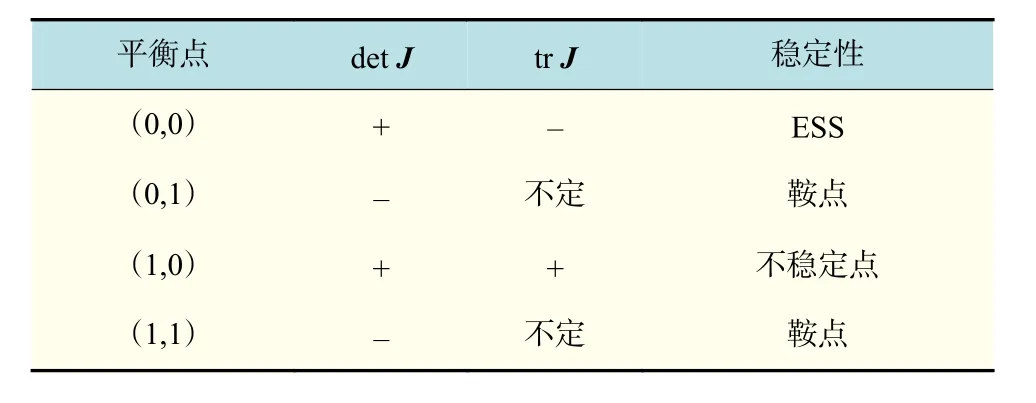
表6 结论2情况2的平衡点局部稳定性Tab.6 Local stability of the equilibrium point in case 2 of conclusion 2

通过以上3种不同情况的分析，归纳得到结论2。结论2说明：当地方政府的积极作为虽未促成企业的回收行为，但仍得到的公众认可或社会声望，与地方政府不鼓励政策下低值可回收物的收运成本、处理成本三者之和，小于地方政府采取鼓励政策时低值可回收物的收运成本和处理成本两者之和；企业资源化利用的经济收益小于地方政府采取不鼓励政策下企业资源化利用的全部成本；且不同时满足地方政府的积极作为得到上级政府的奖励以及享有公众认可或社会声望之和，大于地方政府对回收企业的补贴和低值可回收物的收运成本两者之和；也不满足企业资源化利用的经济收益和地方政府给予的补贴两者之和，大于地方政府采取鼓励政策下企业资源化利用的全部成本时，企业的行为选择将全部趋向于不回收，政府的行为选择将趋向于不鼓励。

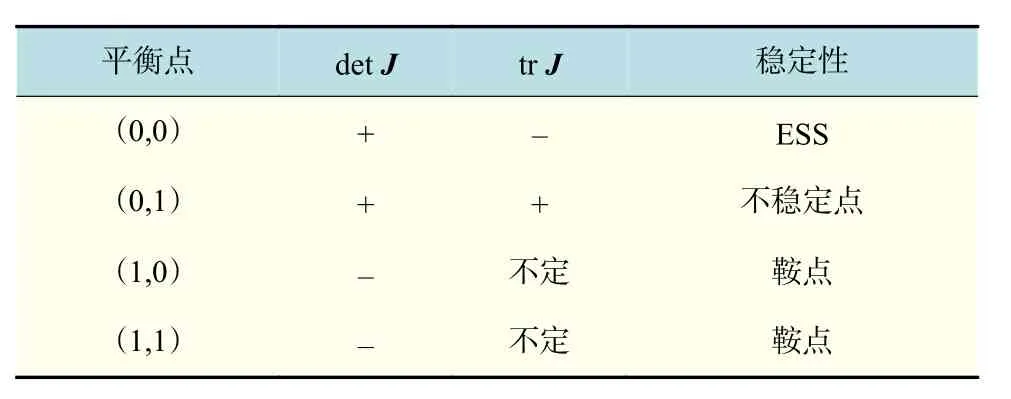
表7 结论2情况3的平衡点局部稳定性Tab.7 Local stability of the equilibrium point in case 3 of conclusion 2

证明 同理，分两种情况讨论。

情况1 当 S− C1−C3+C2+C4＜0， Q −R1＞0，S′−A−C1＜0时，平衡点分析如表8所示。此时系统存在唯一演化稳定策略（0，1），（0，0）和（1，1）为系统的鞍点，（1，0）为不稳定点。这种情况下，政府的行为选择将最终演化为不鼓励策略，企业的行为选择将最终演化为回收策略。

表8 结论3情况1的平衡点局部稳定性Tab.8 Local stability of the equilibrium point in case 1 of conclusion 3

S−C1−C3+C2+C4＞0Q−R1＞0

情况2 当 ， ，S′−A−C1＜0时，平衡点分析如下页表9所示。此时系统存在（1，0）和（1，1）两个鞍点，（0，0）一个不稳定点，系统的演化稳定策略仍为（0，1）。

通过以上两种不同情况的分析，归纳得到结论3。结论3说明：当企业资源化利用的经济收益大于地方政府采取不鼓励政策下企业资源化利用的全部成本；地方政府的积极作为得到上级政府的奖励以及享有公众认可或社会声望之和，小于地方政府对回收企业的补贴和低值可回收物的收运成本两者之和时，企业的行为选择将全部趋向于回收，政府的行为选择将趋向于不鼓励。S−C1−C3+C2+C4＞0Q+A−R2＜0

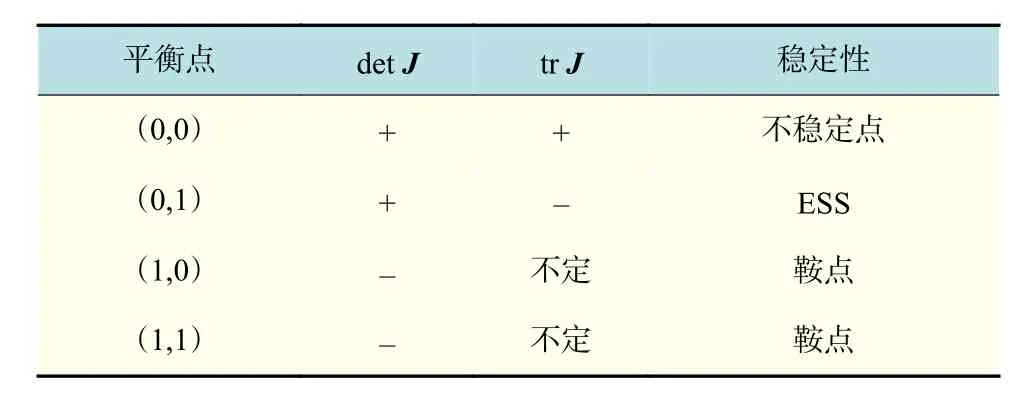
表9 结论3情况2的平衡点局部稳定性Tab.9 Local stability of the equilibrium point in case 2 of conclusion 3

结论4 若满足 ，，则系统的演化稳定策略为（1，0）。

证明 同理，分两种情况讨论。

情况1 当 S −C1−C3+C2+C4＞0， S′−A−C1＜0，Q+A−R2＜0时，平衡点分析如表10所示。此时系统存在唯一演化稳定策略（1，0），（0，0）和（0，1）为系统的鞍点，（1，1）为不稳定点。这种情况下，政府的行为选择将最终趋向于鼓励策略，企业的行为选择将最终趋向于不回收策略。

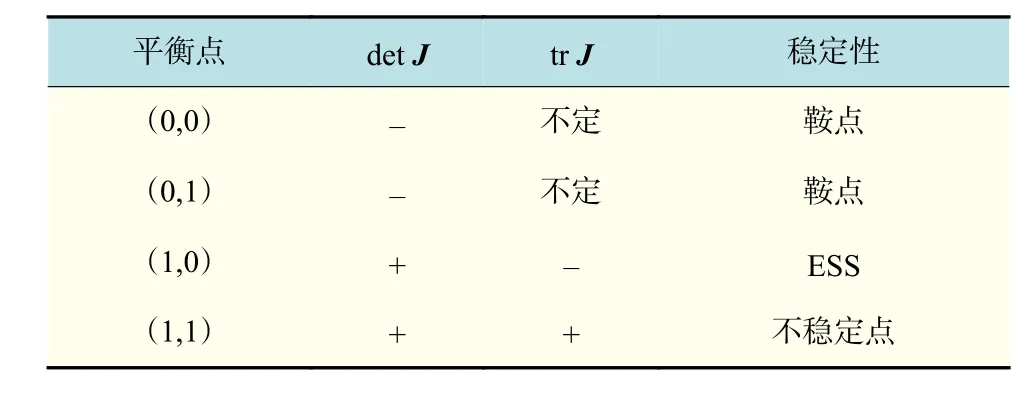
表10 结论4情况1的平衡点局部稳定性Tab.10 Local stability of the equilibrium point in case 1 of conclusion 4

情 况 2 当 S − C1−C3+C2+C4＞0， S′−A−C1＞0Q+A−R2＜0， 时，平衡点分析如表11所示。此时系统存在（0，0）和（1，1）两个鞍点，（0，）一个不稳定点，系统的演化稳定策略仍为（1，0）。

通过以上两种不同情况的分析，归纳易得结论4。结论4说明：当地方政府的积极作为虽未促成企业的回收行为，但仍得到的公众认可或社会声望，与地方政府不鼓励政策下低值可回收物的收运成本、处理成本三者之和，大于地方政府采取鼓励政策时低值可回收物的收运成本和处理成本两者之和；企业资源化利用的经济收益和地方政府给予的补贴两者之和，小于地方政府采取鼓励政策下企业资源化利用的全部成本时，企业的行为选择将全部趋向于不回收，政府的行为选择将趋向于鼓励。

表11 结论4情况2的平衡点局部稳定性Tab.11 Local stability of the equilibrium point in case 2 of conclusion 4

结 论5 若 满 足 S − C1−C3+C2+C4＜0，Q−R1＜0，S′−A−C1＞0 ， Q +A−R2＞0，则系统的演化稳定策略为（1，1）和（0，0）。

证明 同理，平衡点分析如表12所示。此时系统存在两个演化稳定策略（1，1）和（0，0），以及两个不稳定点（0，1）和（1，0）。这种情况下，政府和企业的行为选择或者最终趋向于（不鼓励，不回收），或者最终趋向于（鼓励，回收）。

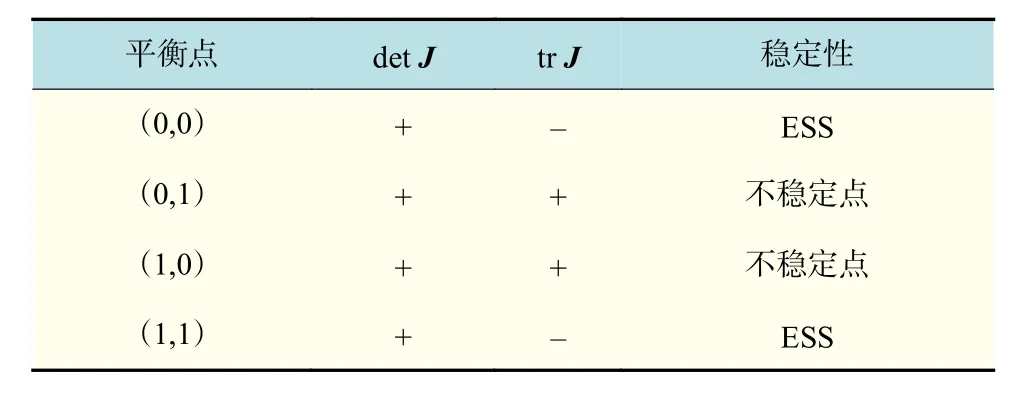
表12 结论5平衡点局部稳定性Tab.12 Local stability of the equilibrium point of conclusion 5

结论5说明，此种情况下政府和企业的演化稳定策略与各自策略的初始概率有关，如图2所示，当政府和企业策略的初始概率值落在由E2（0，1），E5（m，n），E3（1，0），E4（1，1）连成的折线所围成的区域A时，系统的演化稳定策略为（1，1），即政府的行为将最终演化为鼓励策略，企业的行为最终演化为回收策略。与之相对应，当政府和企业的策略初始概率值落在由E2（0，1），E5（m，n），E3（1，0），E1（0，0）连成的折线所围成的区域B时，系统的演化稳定策略为（0，0），即此时政府和企业的行为选择将最终趋向于（不鼓励，不回收）。同时，可以通过调整不同参数的取值，使E5（m，n）的坐标位置发生变化，从而改变区域A，B的面积大小，使系统初始状态落在相应区域的概率增大或减小，促使系统更容易达到预期的均衡状态。

图2 结论5的演化趋势分析图Fig.2 Evolutionary trend analysis diagram of conclusion 5

结论6 若满足 S − C1−C3+C2+C4＞0， Q−R1＜0，S′−A−C1＜0，Q+A−R2＞0 ，所有的平衡点都不能同时满足 det J＞0，tr J＜0 的条件，故不存在系统演化稳定策略。此时平衡点分析如表3所示。

表13 结论6的平衡点局部稳定性Tab.13 Local stability of the equilibrium point of conclusion 6

结论6说明，当满足上述条件时，政府和企业的行为选择都无法趋向于一个稳定点，整个系统处于周期震荡状态。

综合上述6个结论，将6个结论各种条件下的ESS归纳如表14所示。

表14 不同条件下的ESS总结Tab.14 ESS under different conditions

3 仿真分析

本文对地方政府和低值可回收物资源化企业的博弈过程进行了理论上的建模和演化稳定性分析，为了更加直观地理解政府与企业博弈的演化路径和最终的稳定状态，本文用Matlab软件对该演化博弈模型进行仿真，对前述模型作进一步分析。

根据表14的总结结果，本文选取了以下6组数据来验证上述博弈过程的演化稳定策略。

图3描述了各参数满足表14中条件1的演化 趋 势。设定参数值 S=2， S′=6，C1=3，W=3，分别取 x ， y 的初始值为（0.3，0.7），（0.6，时系统C2=2， C3=2， C4=3， R1=4， R2=3， A=2， Q=3，0.4），（0.8，0.2），（0.9，0.1）。结果表明，无论政府和企业选择各自策略的初始概率如何，政府的行为最终演化为选择鼓励策略，企业最终演化为选择回收策略。

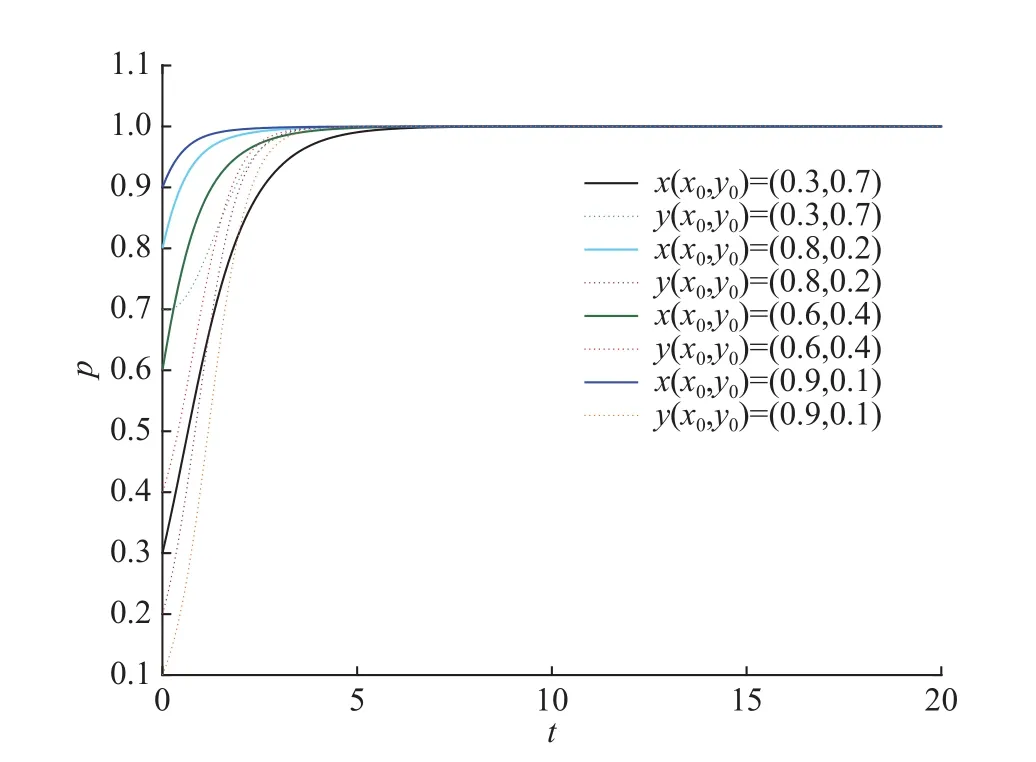
图3 条件1时的演化结果Fig.3 System evolution results when condition 1 is met

图4描述了各参数满足表14中条件2时系统的演化趋势。设定参数值 S=1，=3，C1=4，C2=1， C3=3， C4=4， R1=4， R2=3， A=2， Q=3，W=3，分别取，的初始值为（0.3，0.7），（0.6，0.4），（0.8，0.2），（0.9，0.1）。结果表明，无论政府和企业选择各自策略的初始概率如何，都将最终演化为政府选择不鼓励策略，企业选择不回收策略。

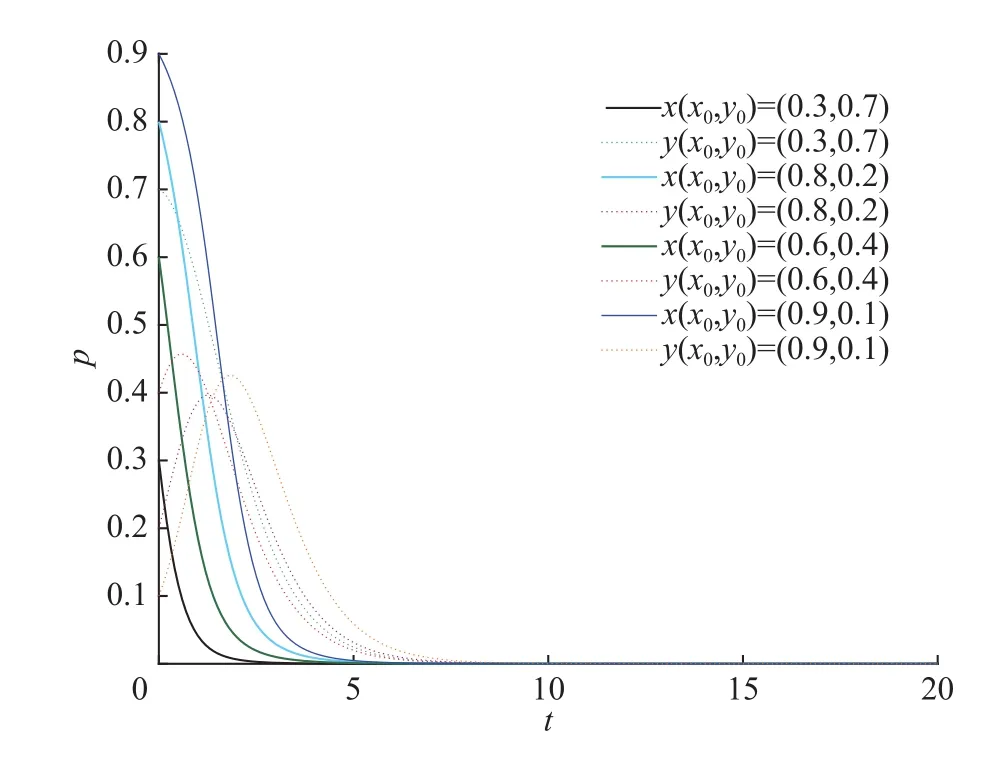
图4 条件2时的演化结果Fig.4 System evolution results when condition 2 is met

图5 描述了各参数满足表14中条件3时系统的演化趋势。设定参数值 S=2，=3，C1=4，C2=2， C3=3， C4=4， R1=4， R2=3， A=2， Q=5，W=3，分别取，的初始值为（0.3，0.7），（0.6，0.4），（0.8，0.2），（0.9，0.1）。结果表明，无论政府和企业选择各自策略的初始概率如何，都将最终演化为政府选择不鼓励策略，但企业选择回收策略。

图5 条件3时的演化结果Fig.5 System evolution results when condition 3 is met

图6 描述了各参数满足表14中条件4时系统的演化趋势。设定参数值 S=2，=3，C1=3，C2=2， C3=2， C4=3， R1=5， R2=4， A=1， Q=2，W=3，分别取，的初始值为（0.3，0.7），（0.6，0.4），（0.8，0.2），（0.9，0.1）。结果表明，无论政府和企业选择各自策略的初始概率如何，都将最终演化为政府选择鼓励策略，企业选择不回收策略。

图6 条件4时的演化结果Fig.6 System evolution results when condition 4 is met

图7 描述了各参数满足表14中条件5时系统的演化趋势。设定参数值 S=1，=8，C1=5，C2=2， C3=5， C4=6， R1=4， R2=3， A=2， Q=3，W=3，分别取，的初始值为（0.1，0.8），（0.2，0.2） ， （0.5， 0.3） ， （0.3， 0.7） ， （0.8， 0.2） ，（0.6，0.7）。结果表明，政府和企业的演化稳定策略与政府和企业选择各自策略的初始概率有关。前三组初始值落在图2的B区域，系统最终演化稳定在（0，0），后三组初始值落在图2的A区域，系统最终演化稳定在（1，1）。

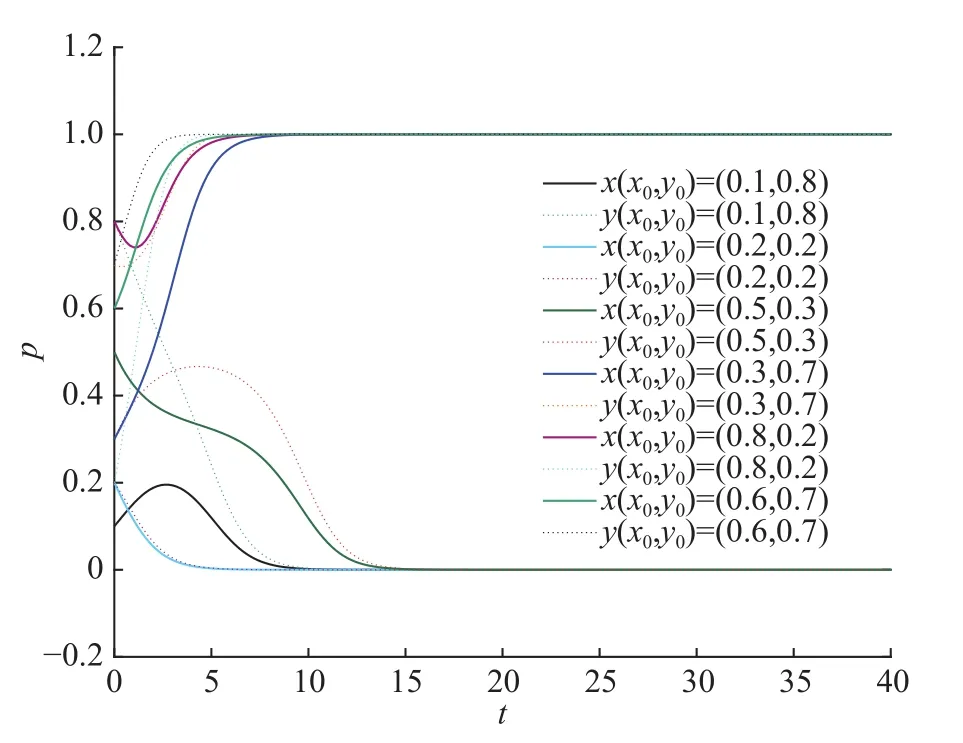
图7 条件5时的演化结果Fig.7 System evolution results when condition 5 is met

图8描述了各参数满足表14中条件6时系统的演化趋势。设定参数值 S=2，=3，C1=4，C2=2， C3=3， C4=4， R1=4， R2=3， A=2， Q=3，W=3，分别取，的初始值为（0.3，0.7），（0.6，0.4），（0.8，0.2），（0.9，0.1）。结果表明，政府和企业的行为选择均无法趋于某一稳定点，整个系统处于周期震荡状态。

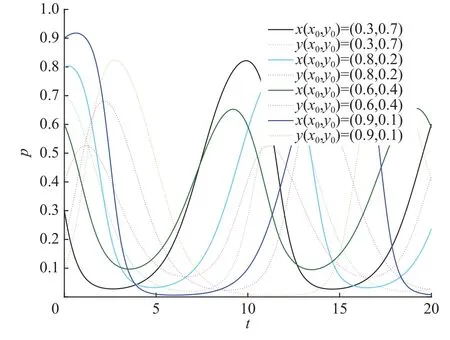
图8 条件6时的演化结果Fig.8 System evolution results when condition 6 is met

4 结论与展望

本文利用演化博弈工具构建了政府、企业为博弈主体的低值可回收物治理的演化博弈模型，并进行了系统演化均衡状态的理论分析和仿真模拟。结果表明：单一群体的均衡点稳定性除了与自身策略有关，还受其他群体的策略影响；当低值可回收物价值较高且回收成本较低时，回收企业有利可图，可回收物的资源化可以靠市场机制调节；随着低值可回收物资源化成本升高和资源化利用价值降低，单靠市场机制难以调动低值可回收物处理企业积极性，难以有效回收处理。以上结论较好地揭示了近些年造成我国低值可回收物回收利用率低，生活垃圾减量形势日益严峻的主要原因在于低值可回收物资源化缺乏引导机制，造成其回收利用收益小于回收利用的成本，最终形成企业不参与低值可回收物治理的行为。基于以上分析，本文给出相关对策如下：

a. 加强政府在低值可回收物处理中的主体地位。在低值可回收物处理中，政府的引导十分重要，政府可建立低值可回收物目录并设立专项补贴资金，加大对低值可回收物市场运行情况的监测，建立综合效益评估机制，根据评估结果动态调整补贴品种和金额。

b. 通过“两网融合”降低低值可回收物收运物流成本。低值可回收物收运成本在资源化利用总成本中占比较大，政府可以通过垃圾回收与再生资源回收两网融合来降低低值可回收物收运企业物流成本，实现低值可回收物有效回收利用。

c. 通过鼓励再生材料和产品应用来提高再生产品的价格。政府可以将再生资源产品纳入政府采购目录，同时加强舆论宣传引导，提高公众环保意识和对再生材料、产品的认可度。