改进的粒子群算法的小波支持向量机预警模型

苗旭东，魏连鑫

（上海理工大学 理学院，上海 200093）

企业财务困境预警是以企业财务信息为基础，通过分析一些敏感性财务指标的变化，对可能面临财务危机的企业进行预测。最早的财务困境预警模型是1932年文献[1]提出的单变量破产模型，该研究表明，净利润/股东权益和股东权益/负债这两项财务指标具有较高的判别能力。1966年Beaver最早提出用统计方法研究财务困境[2]，发现具有良好预测性的财务指标分别为：现金流量、负债总额、资产收益和资产负债率。同年，Altman利用5个财务指标得到财务预警判别方程[3]，得到企业产生财务风险的临界值Z=1.8。1996年文献[4]建立了分数模型，对上市公司财务风险状况进行研究，结果显示，我国上市公司的值的临界点为0.024 7，值低于0.024 7的公司将逐步陷入困境，直至破产；相反，高于0.024 7的公司将健康发展。1980年Ohlson利用Logistic模型进行财务风险预测[5]，模型预测准确率高达96.12%，但是，此模型计算复杂，且众多参数需要取近似值。近年来，神经网络模型[6]得到广泛使用，它具有自学习能力、容错能力和高度并行计算能力，数据间的自相关性以及个别数据的缺失对预测结果影响不大，且自学习性可以对反馈出的错误进行调整。2004年刘洪等使用BP神经网络建立了预测模型[7]，取得了非常高的预测精度，但是，该方法的通用性不强，应用不方便，预测过程中结构难以确定。20世纪90年代Vapnik 提出了支持向量机（SVM）[8]，它以统计学习理论、VC维理论和结构风险最小为基础，在非线性、小样本和高维模式识别中具有独特优势，有效地克服了维数灾难、过学习等问题，比神经网络具有更大的优越性。

在支持向量机模式识别[9]中，SVM的非线性能力可以通过核映射来实现，支持向量机核函数必须满足Mercer定理[10]。在实际应用中，高斯核函数（RBF核函数）应用广泛，然而，由于核函数并非完全正交基，所以，不能任意逼近空间中的曲线，从而SVM不能逼近空间中的任意函数，使得在SVM分类中，不能逼近任意函数。由于小波函数可以通过伸缩和平移建立正交基，并且在空间中有任意逼近的能力，本文在此基础上引入了小波核函数，小波核函数在空间中逼近任意函数，使得SVM具有较强的泛化能力。

1 小波支持向量机

1.1 小波核函数

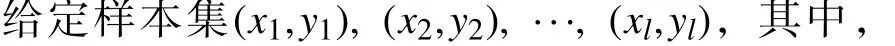
构建平移不变小波核函数

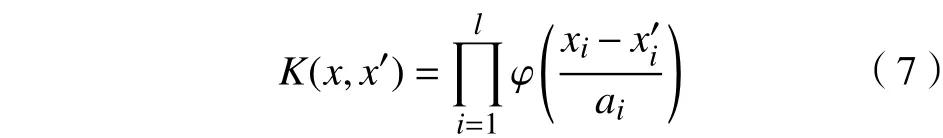
由于很难将这种函数分解成2个不同函数的点积形式，因此，可采用定理2的允许条件，判断小波函数是否为核函数。现给出一个具体的小波函数：Morlet小波核函数，其表达式为

推论1 Morlet小波核函数

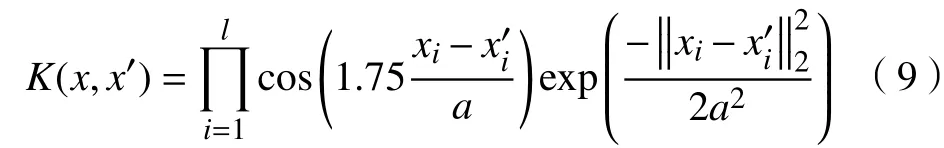
为可允许的支持向量核函数，其中， x ∈ Rl×d,xi∈Rd。

现证明推论1。

证明 由定理2的允许条件a≠0F(ω)≥ 0

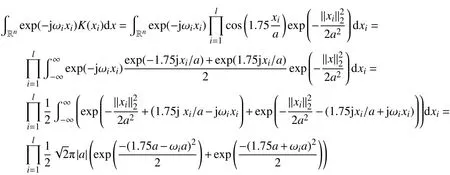
而a ≠ 0，故F(ω) ≥ 0。

1.2 小波支持向量机

小波函数与支持向量机组合，构成小波支持向量机。对于给定的训练集 {(x1,y1),···,(xl,yl)}∈ {1,−1},i=1,2,···,l l n为样本数， 为输入维数，得到WSVM算法。原始问题：

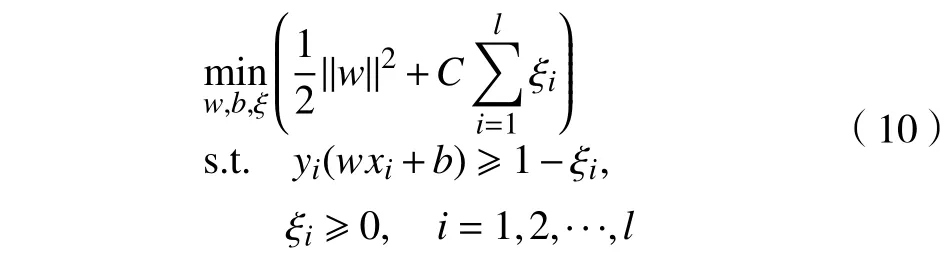
式中，C为惩罚参数。

为了得到原始问题（10）的对偶问题，引出Lagrangian函数。

则原始问题（10）的对偶问题为

选择适当的参数 和核函数参数 ，得到WSVM决策函数

2 改进的粒子群优化算法

WSVM模型中存在2个需要确定的参数：惩罚参数 ，小波核函数参数 。它们的取值与预测精度有很大关系，合适的参数能提高模型的泛化能力，因此，选择一个优化算法对参数进行优化很有必要。

粒子群算法（PSO）在组合优化问题中具有突出的性能，是一种基于速度−位置搜索的智能优化算法，在每一次迭代中，粒子不仅考虑到自己搜索的历史最优点best，还考虑到群体内其他粒子的历史最优点 Gbest，以便找到问题最优解.在标准PSO算法中，粒子的速度、位置更新的迭代公式为W

惯性权重 的大小决定了粒子对当前速度继承的多少，惯性权重较大，粒子在原方向上具有较大速度，则在原方向上飞行更远，具有较好的探索能力；惯性权重较小，粒子在原方向上具有较小速度，则在原方向上飞行较近，具有较好的开发能力，以扩展搜索空间[11]。随着迭代次数的增加，希望有较好的开发能力，使粒子在搜索的最优区域内进行局部搜索，找到最优解.

为了平衡全局与局部搜索能力，通常采用线性时变权重对惯性权重进行调整，即第k次迭代时的惯性权重

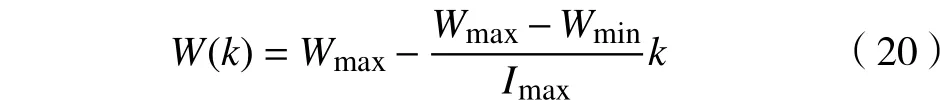
线性时变权重中权重值线性减小、最大迭代次数选取不当，易使惯性权重减小过快，陷入局部极优解，为避免这种情况，本文提出非线性递减惯性权重

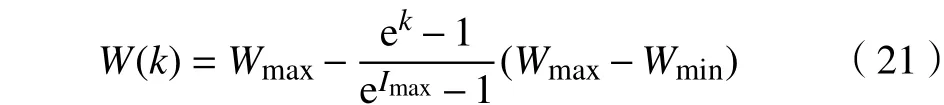
3 基于改进的PSO优化WSVM算法（PSO-WSVM）的预测模型

b. 计算粒子适应度值 f (x)。设置每个粒子个体极值 Pbest为当前位置，由式（18）和式（19）计算粒子适应度值，取最优的个体极值作为最初的全局极值best ；

c. 根据式（18）和式（19）更新粒子速度、位置，若更新速度＞Vmax， Vmax为设定最大更新速度，则取max， 若 V ＜Vmax，则取 V ，并由式（21）更新惯性权重,同时比较粒子个体极值 Pbest与适应度值，若优则更新，否则取原值；

e. 判断寻优是否达到最大迭代次数或评价值小于给定精度，若满足，则将数， a赋给SVM进行训练，否则转步骤b；

f. 利用步骤e优化的参数数 C ， a进行SVM预测，判断预测误差是否达到精度要求，若在精度要求内，则结束预测，否则转步骤a。

4 基于PSO-WSVM的预测实例分析

4.1 数据的处理

现以上市公司因连续两年亏损而被证券交易所特别处理（ST）作为公司发生财务困境的标志，选取了2014，2015两年被ST的上市公司以及正常公司，共367家，为了降低模型被高估的可能性[12]，本文训练和预测数据倒推前两年，即以这些公司2012，2013年的年度财务报表数据作为训练、测试样本，以公司的盈利能力、偿债能力、经营能力、成长能力及现金能力等共12项作为预警财务指标，如表1所示。

由于预选的12个财务指标之间可能存在较强的相关性，利用主成分分析法对这些指标进行筛选，达到降维的效果.借助SPSS软件，得到12个财务指标的成分得分系数，如表2所示。

因此，将 Y1， Y2， Y3， Y4， Y5这5个成分作为模型的自变量，即可得到Y1，Y2，Y3，Y4，Y5的表达式

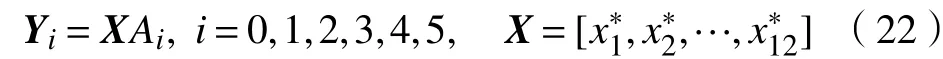
标准化公式为

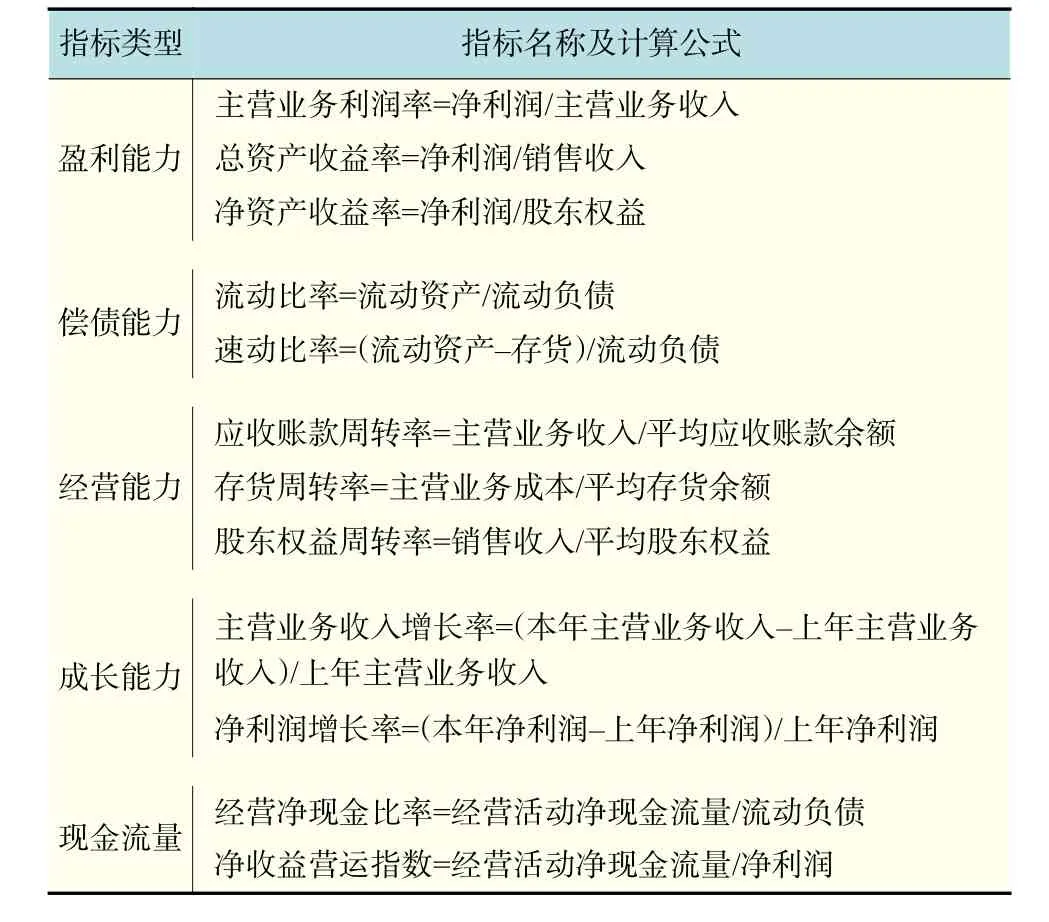
表1 预警财务指标Tab.1 Early warning financial indicators

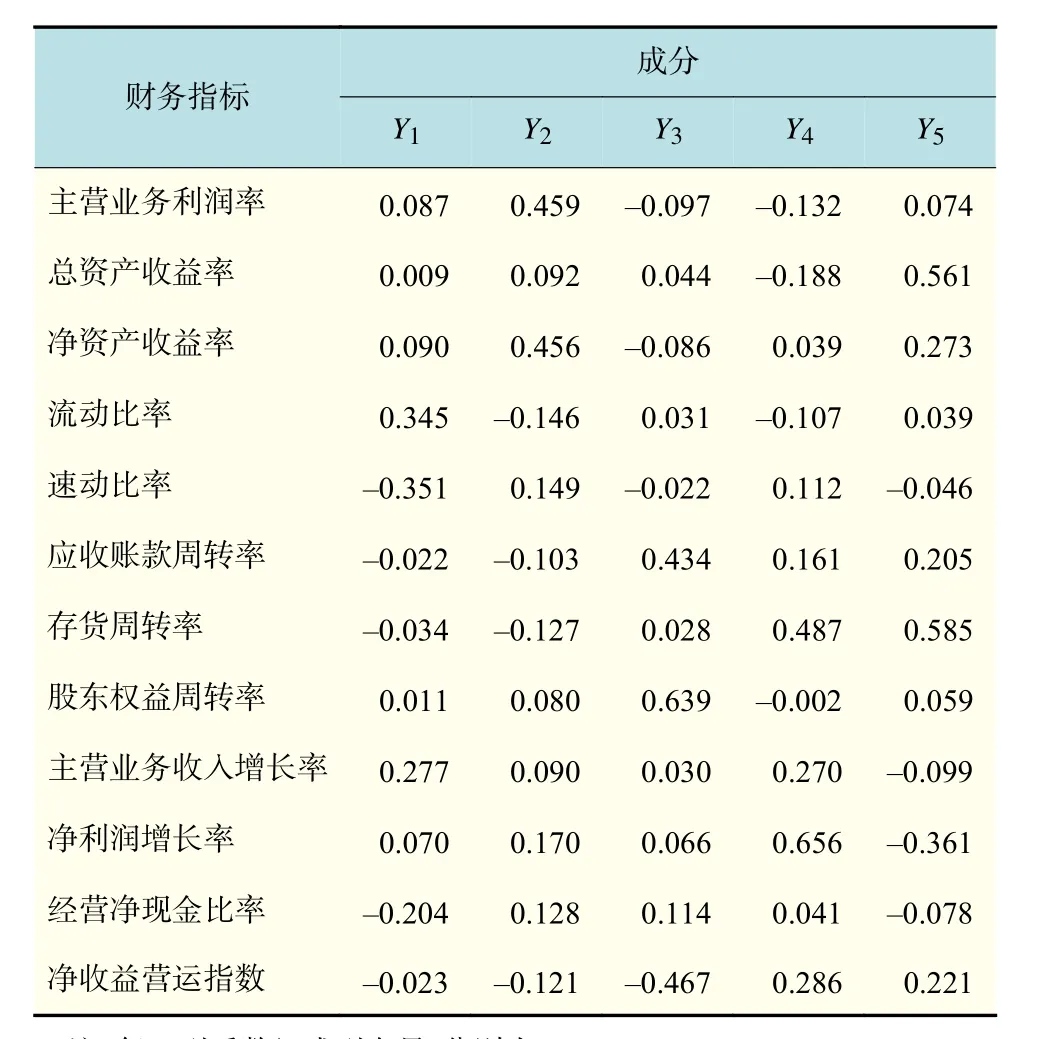
表2 成分得分系数矩阵Tab.2 Component score coefficient matrix

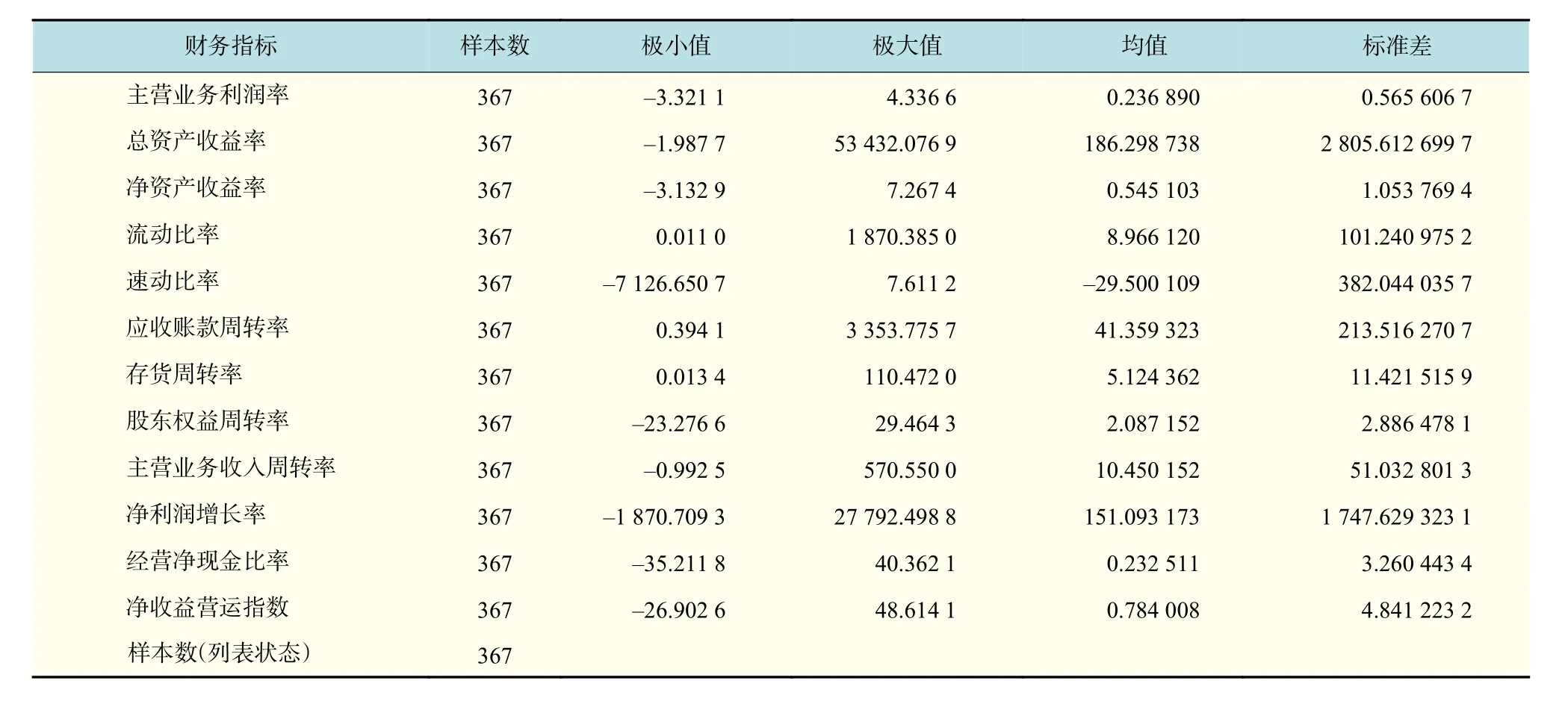
表3 财务指标均值、标准差Tab.3 Means and standard deviations of financial indicators

4.2 模型的建立与预测

现介绍本文模型参数的训练结果以及优化后参数的预测结果。

a. PSO算法初始参数的设置：最大迭代次数20，种群规模20，学习因子=c2=1.3，最小、最大惯性权重min,max分别为0.1，0.9，适应精度为 0.000 1；

b. 利用改进的PSO算法、PSO算法分别对惩罚参数C，核函数参数a进行优化，利用计算机软件对模型进行训练（取367家上市公司的财务数据作为模型的仿真数据（其中有285家公司为健康公司，82家为被ST的公司），并取前347个数据作为训练集，后20个数据作为测试集（11家健康公司，9家被ST公司），为了进行对比，分别选Morlet小波核函数、RBF核函数、线性核函数、Sigmiod核函数对模型进行训练），通过改进的PSO确定的最优参数C=9.819 4，a=0.6.

c. 预测结果：预测样本的实际值、RBF核函数预测值、线性核函数预测值、Morlet小波核函数预测值、PSO优化的Morlet小波核函数预测值、改进的PSO优化的Morlet小波核函数预测值等的对比结果如表4所示。

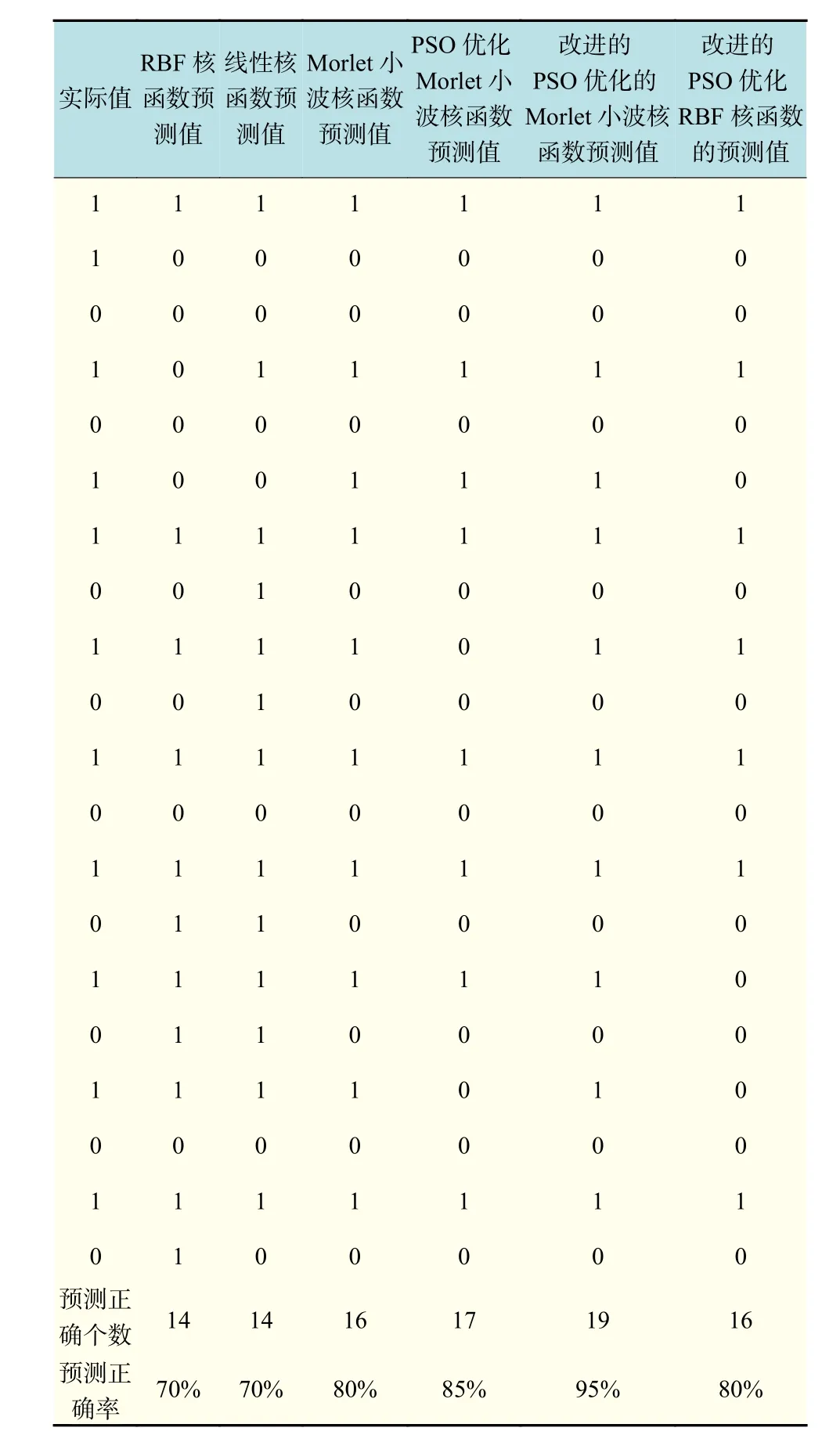
表4 实际、预测值（1表示健康公司，0表示被ST公司）Tab.4 Actual and predicted value (1 for health company, 0 for ST company)

由表4可知，WSVM模型正确分类个数为16个，预测准确率为80%，而核函数分别为RBF、线性核函数的SVC模型正确分类个数都为14个，预测正确率均为70%，而改进的PSO优化核函数为RBF核函数的SVM模型，正确分类的个数为16个，预测准确率为80%，与未利用PSO改进的模型相比较，准确率有所提高；未改进的PSOWSVM正确分类个数为17个，预测准确率为85%，较之前面方法准确率有一定提升，这与小波函数具有任意逼近能力是有关的；而本文改进的PSO-WSVM模型在分类方面具有良好的性能，模型正确分类的个数为19个，预测准确率高达95%，说明惩罚参数C、核函数参数a的正确选择能够大大提高预测准确率。综上所述，本文构建的改进的PSO优化WSVM模型对企业财务困境进行预测的准确率是较高的，能够运用于实际分析中。

5 结束语

提出了基于WSVM的公司财务预警预测方法，并用一种改进的PSO优化算法对模型参数进行寻优，将本文的预测结果分别与PSO优化Morlet小波核函数的预测值和改进的PSO优化RBF核函数的预测值进行了对比，实验结果表明：WSVM是一种有效的建模方法，模型的预测结果与实际结果基本相似，是财务预警分析的有效工具。改进的PSO优化算法更有效果，参数优化后的模型预测准确率提高，表明本文提出的模型具有更好的预测性能。