混合分数阶p-Laplace算子方程积分边值问题的多解性

张潇涵，刘锡平，贾梅，陈豪亮

（上海理工大学 理学院，上海 200093）

1 问题的提出

随着自然科学和社会科学的发展，复杂工程应用需求的增加，分数阶微积分理论及其应用开始受到广泛关注[1-4]。非线性分数阶微分方程起源于核物理、流体力学及非线性光学等应用领域，其理论研究在目前微分方程领域中较为活跃[5-9]。具有 p-Laplace算子的分数阶微分方程边值问题是非线性微分方程的一个重要研究课题，许多学者对不同类型的分数阶微分方程边值问题解或正解的存在性与多重性进行了大量研究[10-17]。由于Riemann-Stieltjes积分边值问题是经典Riemann积分边值问题的推广，两点边值问题、多点边值问题及一般Riemann积分边值问题可视为Riemann-Stieltjes积分边值问题的特例，因此，Riemann-Stieltjes积分边值问题具有更宽广的应用背景[12]。

本文研究一类同时具有Riemann-Liouville导数和Caputo导数的混合型分数阶 p-Laplace算子方程在 Riemann-Stieltjes积分边界条件下的正解的存在性。

2 预备知识及引理

分数阶微积分的相关定义及其结论见文献[2-3]。这里给出几个与本文密切相关的结论。

引理1[3]假设 u ∈C(0,1)∩L(0,1)，则分数阶微分方程(t)=0的解为f Q={(x,y):a≤x≤b,c≤y≤d}(x,y)B [a,b]

引理4[18]设 在矩形区域

的每个点 处连续， 在 上单调递增，那么，

在[c,d] 上连续。

现假设

引理5 令 ξ ∈C[0,1]，则函数 u ∈E 是下面的边值问题的解。

根据引理1和引理2分别得到边值问题（8）和（9）的解为

对式（11）的两边进行Riemann-Stieltjes积分，

将其代入式（11），可得

证明 由函数 G (s,τ)和 Λ (t,s)的表达式容易证得性质a和b。下面证明性质c。

当0≤s≤t≤1时，

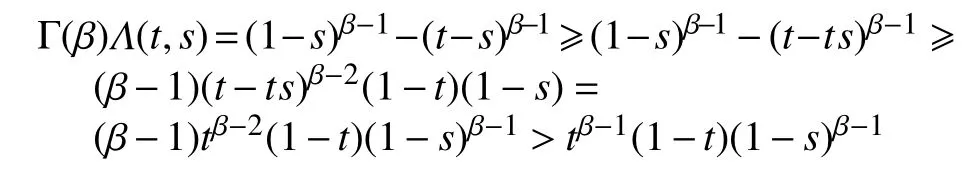
另一方面，有

由引理3可得

证毕。

3 边值问题正解的多重性

因此， A等度连续。

由Arzela-Ascoli定理可知， A :P→P全连续。

证毕。

现作如下记号：

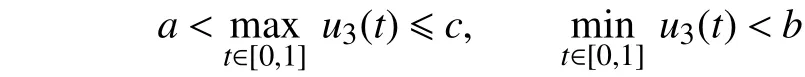
证明 由引理5可知，边值问题（1）等价于积分方程

显然， u =u(t)是边值问题（1）的正解当且仅当u满 足算子方程 u =Au(t)。

首先，证明 A :Pc→Pc全连续。对任意的u∈Pc，由定理1的c，有

最后，证明 µk(t)＜ ωk(t),t∈ [0,1],k=0,1,2,···。

因为， µ0(t)＜ ω0(t),t∈[0,1]，则

µk(t)＜ ωk(t),t∈[0,1],k=0,1,2,···

类似地，可以推出 。证毕。

4 应用举例

现运用所得结论解决几个具体的混合型分数阶p -Laplace算子方程边值问题。

例1 若取

例2 考虑混合分数阶微分方程边值问题