基于格子玻尔兹曼方法的二维T型微通道内液滴生成
2018-09-23王昭君杨帆郭雪岩
王昭君,杨帆,2,郭雪岩,2
(1. 上海理工大学 能源与动力工程学院,上海 200093;2. 上海理工大学 上海市动力工程多相流与传热重点实验室,上海 200093)
微流控技术兴起于20世纪80年代,是一种对微尺度下多相流进行精确操控的技术。自从瑞士Ciba Geigy 公司的 Manz等[1]于 1990 年 首次提 出后,各国的研究人员先后对这一领域进行了研究,并不断与生物、化学及医药等学科相互交叉,产生了大量的革新性成果,在2003年被Forbes杂志评为影响人类未来的15项发明之一。其中,微流控芯片在各个领域中都有着特别的优势,其作为微流控技术的一大应用不仅具有良好的集成性,可以同时平行处理大量样品,而且具有试剂消耗量少、分析速度快、廉价、安全及污染小等优点。尤其是在生物医学研究、环境监测保护及药品合成等领域具有广泛的应用前景。
在Thorsen等[2]首次采用T型微通道生成液滴后,T型微通道便成为微流控装置中液滴生成的一种最常用的方式之一。刘志鹏等[3]发现了射流模态和滴流模态后,分析出液滴生成的主要原因是界面失稳,并可以由较大的黏性剪切力提前激发。Li等[4]通过数值模拟的结果得出T型微通道中的表面张力和黏性力交替支配着液滴的生成,周期性的压力和局部的速度确保均匀的液滴的产生;通过连续相对分散相的剪切力的作用可以生成稳定的液滴,通过改变流量以及能主导微尺度流体运动状态的黏性力和表面张力可以获得不同长度和间隙的液滴。Nunes等[5]研究了T型微通道下液滴的长度和通道直径的比值所得的液滴的相对长度与连续相的毛细数成反比。当增大连续相的流量时,流态会从挤压模态转换成滴流模态,最终变为射流模态。董立春等[6]采用Fluent软件模拟T型微通道中液滴的生成,提出了通道壁浸润性是产生液滴的基本条件,并且进一步论述了液滴的长度与毛细数的倒数之间的正比关系。王澎等[7]应用VOF模型研究了三维T型微通道内毛细数、黏性比对微液滴的破裂过程的影响,得出了一定轴向长度的微液滴对应着液滴破裂的一个临界毛细数。Christopher等[8]认为只有两相黏度相近时,黏度比才会对液滴产生影响,更改黏度比不会影响到模态的转变。
综上所述,T型微通道作为微流控元件生成液滴的基本方式,对液滴生成的尺寸和频率的有效控制是微流控元件能否有效投入生产和使用的基础。通过大量的实验和模拟数据可以得出T型微通道中液滴的尺寸和间距主要受壁面的浸润性、连续相的毛细数、两相流量比、两相的黏性以及表面张力的影响,其中,壁面的浸润性为液滴产生的前提,连续相的毛细数、两相流量比则与液滴尺寸呈明显的函数关系,为主要的影响因素,而调整两相的黏性及表面张力不足以显著改变液滴的尺寸。本文验证了格子玻尔兹曼方法中的伪势模型可以很好地模拟T型微通道内的两相流动,并且得到了几个因素对液滴尺寸影响的数值关系,分析了在模态转变时两相流量比对液滴尺寸的影响。
1 数值方法与模型验证
1.1 数值方法
采用Shan等[9]提出的多组分多相伪势格子玻尔兹曼模型,研究了T型微通道内的液滴形成过程,通过引入固体壁面与流体各组分之间的相互作用来实现壁面的润湿条件(接触角)[10],通过引入流体各组分之间的相互作用来实现对表面张力的控制。对于二维微通道,采用D2Q9模型[11]。根据格子玻尔兹曼方法的伪势模型,每个成分的分布函数由下式决定:

上述方程中格子的离散速度


根据伪势模型,作用于流体间的相互作用力

式中: ψσ(x)表示流体组分 σ的有效密度,同组分的密度有关;σσ¯为格林函数,控制着两组分之间的相互作用强度,当 Gσσ¯为正值时,表示两组分相互排斥,因此,可以选择适当的 Gσσ¯的值来分离不同的组分;,σ分别表示不同的流体组分。
类似地,流体–固体之间的相互作用力
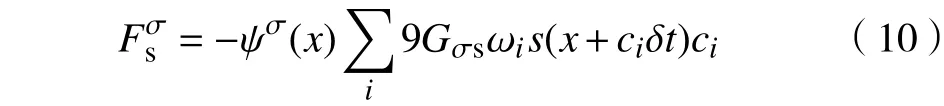
1.2 模型验证
1.2.1 杨–拉普拉斯定律的验证
根据毛细管的拉普拉斯方程可知液滴平衡半径为 的界面内外压差
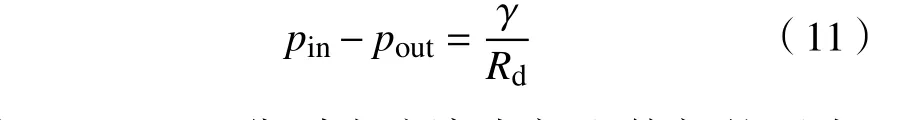
在伪势模型中,表面张力 γ由相互作用强度Gσσ¯决定,为了验证模型并且获得表面张力的具体数值,将不同半径的液滴悬浮在 5 0×50的其他流体空间内,模拟了上下左右都为周期性边界条件的格子区域。在这里选用11=22=−0.15,G12=G21=0.2(1表示连续相,2表示分散相)。模拟结果中液滴界面处的内外压差 pin−pout与液滴平衡半径的倒数/的关系如图1所示,两者的关系可以用斜率=0.122的直线拟合, γ即两组分之间的表面张力。这验证了杨–拉普拉斯定律,在本文接下来的模拟中也采用这些已被验证了的参数。
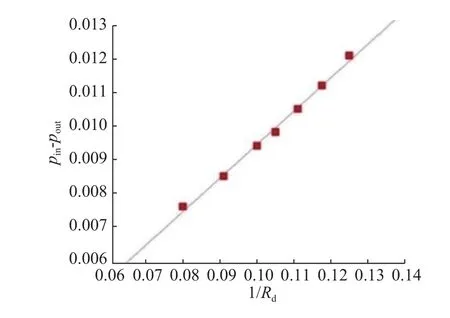
图1 杨−拉普拉斯定律的验证Fig. 1 Validation of the law of Yang Laplace
1.2.2 浸润角验证
通过调节两种不混融的流体与壁面的相互作用强度,即式(10)中的1s和 G2s的数值,可以调节微通道内浸润角的大小。为了验证浸润角和2s之间的关系,同样选择将液滴贴近于下壁面并悬浮在 5 0×50的其他流体空间内,左右为周期性边界条件,上下边界为固壁。控制其他量不变,只改变s的大小,得到接触角 θ和 G2s的关系可以由一条直线来拟合,如图2所示,可以看出,在 G1s=0的情况下,当 G2s=0.15时,液滴对壁面的接触角大于140°,即液滴在墙壁上几乎不润湿,本文接下来的研究即采用上述参数。
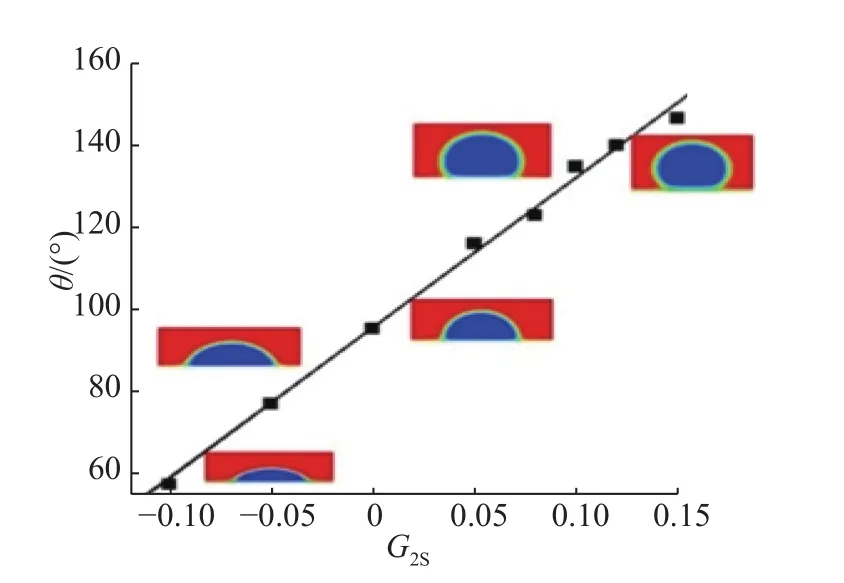
图2 浸润角的验证Fig.2 Validation of the infiltration angle
2 模拟结果
2.1 物理模型
图3(见下页)是本文采用的二维T型微通道示意图,长度L=600,网格总数为12 600,其中,壁面采用标准反弹格式,为疏水性壁面;T型微通道有两个相互垂直的入口,两入口均采用非平衡反弹格式[12],为速度入口,入口与交叉口的间距=y2=30,两入口宽度 W1=W2=20,连续相通过与出口平行的入口通道流入,分散相则通过垂直于连续相入口的通道流入;出口采用非平衡反弹格式,为压力出口。
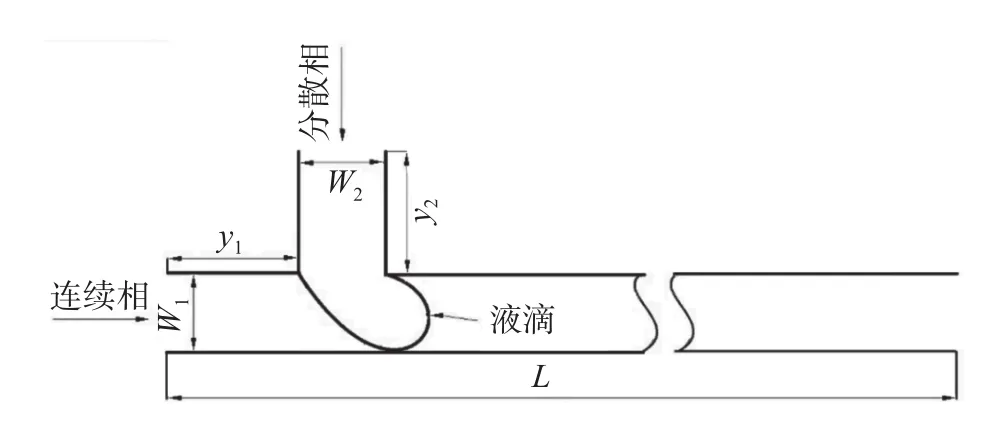
图3 物理模型Fig.3 Physical model
非平衡反弹格式由Zou等[13]1997年首次提出,即假设分布函数的非平衡部分在出入口的边界垂直方向上也满足反弹格式,可以很好地应用于压力和速度的出口条件,图3中分散相的速度
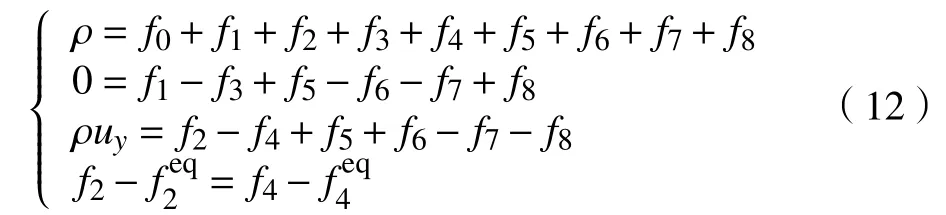
联立求解方程组(12),即可求出在入口边界层上的未知量。

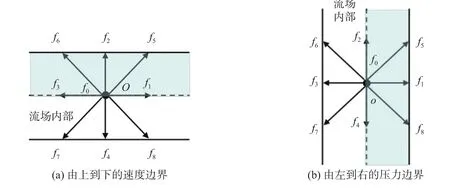
图4 非平衡反弹格式边界Fig.4 Non-equilibrium rebound format boundaries
联立求解方程组(13),即可获得出口处边界层的密度分布函数。用 L1表示液滴长度, L2表示液滴间距,则液滴的相对长度为 L1/W1,液滴的相对间距为 L2/W1。在T型交叉口处,连续相对分散相会产生一个剪切力的作用,当这个剪切力大到足以扰动分散相的界面张力使之失稳时,连续相即突破分散相的界面张力,切断分散相,形成液滴。
2.2 模型正确性验证
魏丽娟等[14]根据实验结果将液滴生成两相流动分为弹状流、过度流和滴状流这3种流态,如图5(a)所示。图5(b)为本文在同一T型微通道模型下采用伪势模型模拟的结果,与实验结果作定性对比,结果表明,本文采用的计算方法和模型基本正确。

图5 3种模态模拟结果与实验结果的对比Fig.5 Comparison of three modal simulation results and experimental results
在同样的模型下,将本文的模拟结果与魏丽娟等[14]的实验结果作定量对比,图6为通过实验获得的连续相的毛细数 C a 和液滴的相对长度L1/W1之间的关系,通过液滴的长宽比来划分3种不同的模态。若L1/W1>1.5,即为弹状流;若1.5>L1/W1>,为过渡流;若 L1/W1<1,即液滴不能占满通道的宽度,此时为滴状流。图7为本文的模拟结果,可以看出,本文的模拟结果和实验结果基本相吻合。可以认定本文采用的计算模型的正确性,即格子玻尔兹曼伪势模型可以很好地模拟型微通道中液滴的生成。vd为分散相入口速度。
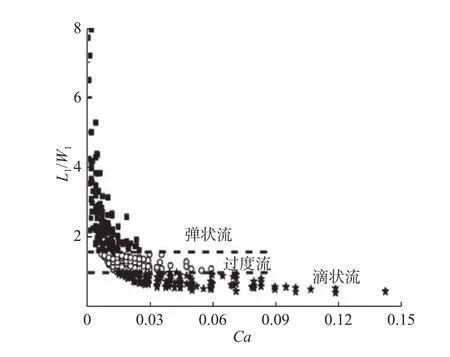
图6 实验中毛细数与液滴的相对长度的关系Fig.6 Relationship between the capillary number and the relative length of droplet in the experiment
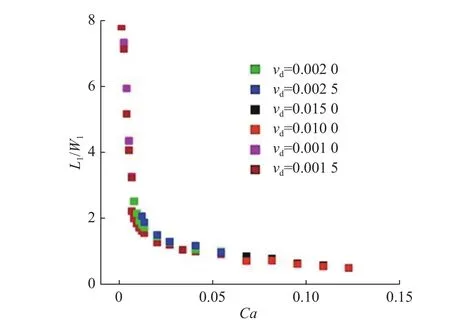
图7 模拟结果所得毛细数与液滴的相对长度的关系Fig.7 Simulation of the relationship between the capillary number and the relative length of droplet
2.3 毛细数对分散相生成的影响
Ca
毛细数Ca是一个无因次数,同黏性和表面张力成正比,反映了表面张力和黏性对液体流动的影响,本文中的Ca均指连续相的毛细数。本文的研究主要是在微尺度下进行的,故液滴的惯性力可以忽略不计,即表面张力和黏性对液体的流动起着至关重要的作用。液滴生成的长度主要受毛细数 的影响。本文在固定3种不同的分散相入口速度下探讨连续相的毛细数与液滴的相对长度L1/W1之间的关系,得到如图8所示的结果。
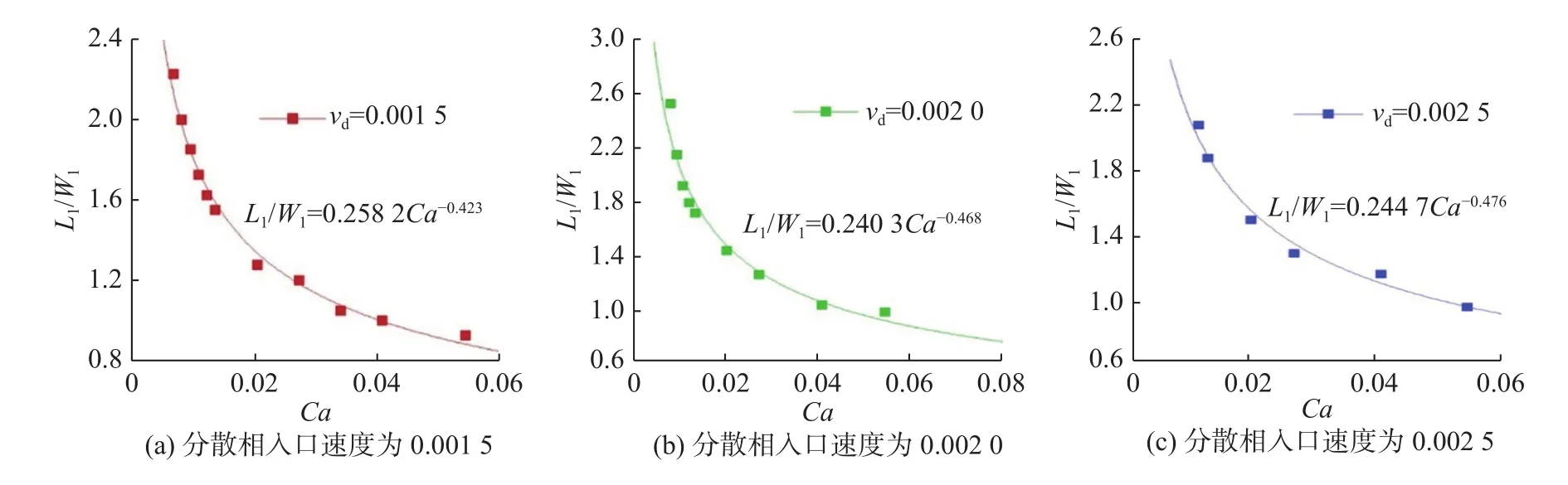
图8 不同分散相速度下毛细数与液滴的相对长度的关系Fig.8 Relationship between capillary number and the relative length of droplet at different disperse phase velocities
在不同的分散相入口速度下,连续相的毛细数与液滴的相对长度 L1/W1之间存在幂律关系,即通式:

式中,参数A,B由两相的物性、通道的尺寸等决定,分散相的速度对A,B两参数几乎没有影响。
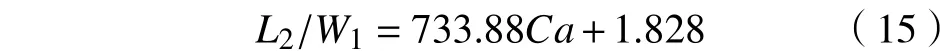
2.4 两相流量比对分散相生成的影响
液滴尺寸随两相流量比 β 的增大而增大,β=qd/qc, 其中, qc为连续相的流量, qd为分散相的流量。由图10(见下页)可以看出,当L1/W1<1.8时, L1/W1和 β成正比关系,符合前人总结的液滴的相对长度与流量比关系的一般通式:

式中,参数PQ和 由两相的物性、通道的尺寸等决定。
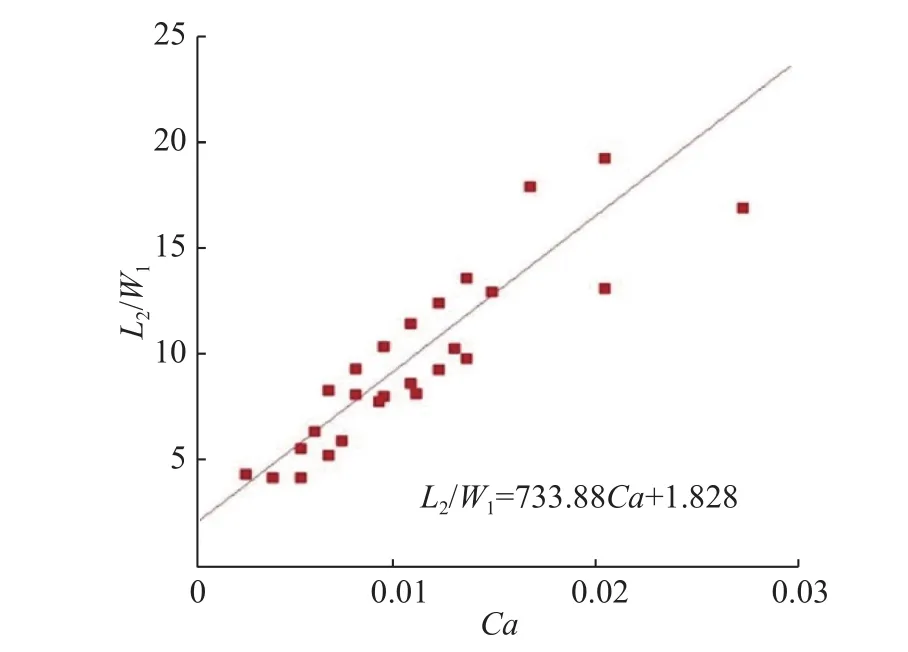
图9 毛细数与液滴的相对间距的关系Fig. 9 Relationship between the capillary mumber and relative spacing of droplet

图10 两相流量比与液滴的相对长度的关系Fig.10 Relationship between the flow ratio and relative length of droplet
由本文的模拟结果得到参数值 P =4.557 4,Q =0.784 5。但是,当 L1/W1>1.8时,即在挤压模态下,液滴的尺寸和两相流量比就没有明显的逻辑关系了。
两相流量比对液滴间距的影响如图11所示,可以看出,两相流量比和液滴的相对间距之间存在幂律关系:

2.5 连续相的黏性对分散相生成的影响
液滴的尺寸随着连续相黏性的增大而减小。连续相黏度变大,使得连续相对分散相的剪切力变大,导致分散相的界面张力很快失稳,分散相提前断裂,生成的液滴的长度变短,当连续相速度为0.02,分散相的速度为0.000 2时,改变连续相黏度 µ,可以看出,液滴的尺寸随着 µ的增大而略微变短,两者呈现出负相关关系,如图12所示。对于连续相黏度对间距的影响,从图13可以直观地看出,增大连续相的黏度,液滴的间距也在逐步变大,连续相黏度和液滴间距呈正比例关系,但其产生的影响幅度较小。
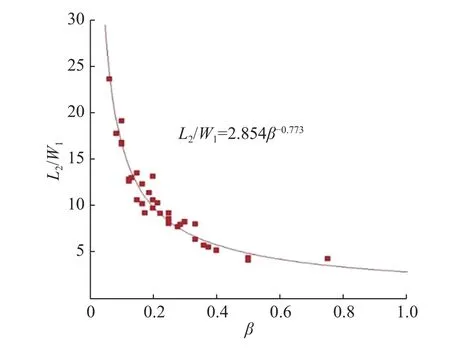
图11 两相流量比与液滴的相对间距的关系Fig. 11 Relationship between the flow ratio and relative spacing of droplet
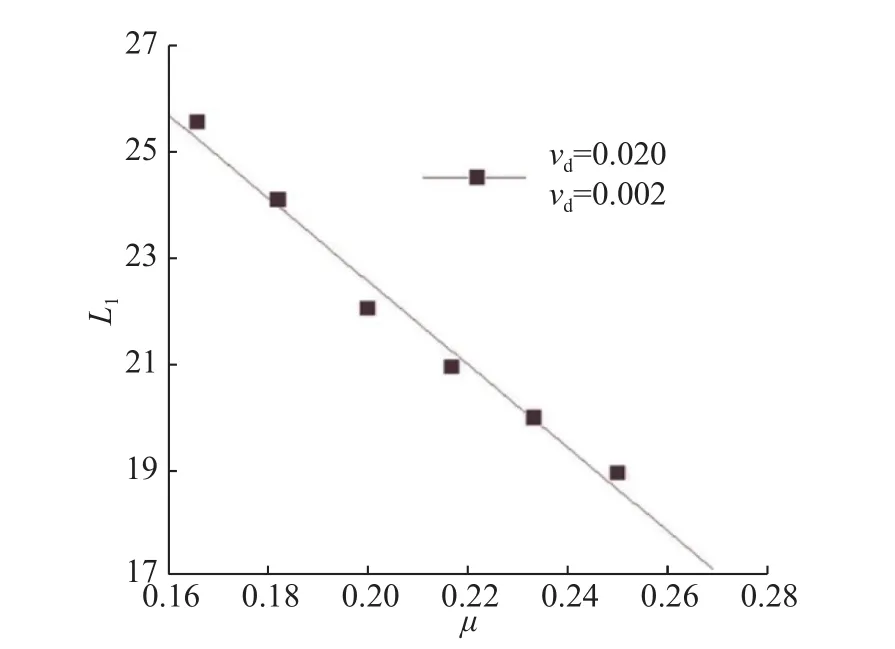
图12 黏度与液滴长度的关系Fig. 12 Relationship between the viscosity and droplet length
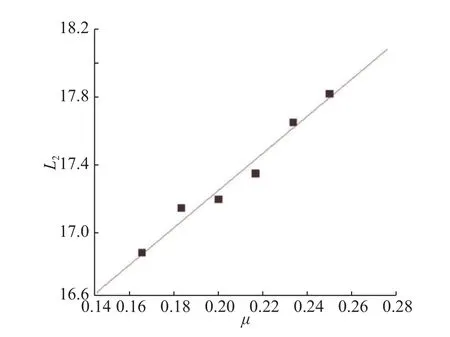
图13 黏度与液滴间距的关系Fig. 13 Relationship between the viscosity and droplet spacing
3 结 论
采用多组分多相伪势格子玻尔兹曼模型对T型微通道内液滴的生成进行数值模拟,探讨了毛细数、两相流量比、黏度这3个因素对液滴长度的影响,可得结论:
a. 毛细数与液滴的相对长度确实存在着幂律关系,且与液滴的相对间距呈正比关系;
b. 两相流量比在滴状流和过渡流与液滴的相对长度呈正比关系,但是,在弹状流下其影响却变得不太明显,即当两相的流量大小越来越相近时,流量比对液滴尺寸的影响幅度越小。流量比对液滴间距的影响不受两相流型转变的影响,它们之间呈现出一种幂律关系,当流量比变大时,间距变小。
c. 当两相的黏度比较接近时,连续相的黏度对液滴尺寸影响较小;在连续相黏度变大时,液滴尺寸会相应地减小,同时液滴间距会略微变大。
采用的T型微通道模型为二维模型,而真实的实验是三维的,因此,模拟所得的结果与实验略有差距,为进一步提高精度,将来应采用三维模型模拟,使其更加符合真实情况。
