具有学习退化效应的TFT-LCD面板成盒多目标调度问题研究

吴思思，叶春明，李瑞婷

（上海理工大学 管理学院，上海 200093）

薄膜晶体管液晶显示器（thin-film transistorliquid crystal display，TFT-LCD）是液晶显示器领域中最重要的一种显示器，被广泛应用于手机、平板电脑、彩电等显示领域。TFT-LCD产品生命周期短，制造流程复杂，快速满足消费者不同需求是企业核心竞争的关键要素。这需要生产企业合理安排不同类产品同时进行加工，保障交货期的前提下，有效利用机器，缩短生产周期。本文以最小化最大完成时间、机器等待时间、工件加权延期时间为优化目标，通过多目标布谷鸟算法（multiobjective cuckoo algorithm， MOCS） 求 得 该 问题帕累托非劣解集，为TFT-LCD生产企业更有效地安排生产资源、提高企业竞争力提供理论基础。

1 研究现状

在TFT-LCD调度优化领域，国内外学者主要侧重于对下游TFT-LCD制造中模块组装（Module）制程的研究[1-3]，上游阵列制造（Array）制程的研究文献相对较少[4-5]，中间制程面板成盒（Cell）制程的研究文献也相对匮乏。Lin等[6]通过改进加工物品单位Lot的发放时间及派发规则，提高Cell阶段生产效率。徐峰等[7]提出改进遗传算法，解决Cell阶段具有设备准备时间的工件调度问题。Wu等[8]提出基于约束理论的“鼓—缓冲—绳”系统，应用于Cell阶段的定制模型，通过平衡生产线工作负荷水平，提高Cell阶段生产效率。Yang等[9]通过对Cell后半段贴偏光板到COG(Chip-on-Glass)工站进行Arena仿真建模，并结合神经网络方法，实现多目标动态调度优化。目前，在Cell制程部分，TFT-LCD研究较为薄弱，缺少对Cell制程整个生产工艺流程的多目标调度研究，且传统求解方法计算复杂，结果单一，也很少见到将行为效应应用在TFT-LCD调度问题中。

在实际生产过程中，随着加工时间增加，工人或机器的单个工件加工时间逐渐缩短；但当机器被安排加工的工件还未完成前道工序，或更换不同产品簇而产生等待时间时，累计的学习效应将减弱，再加工工件的实际加工时间增加。前者称为学习效应，由Wright[10]提出，后者称为退化效应。Biskup[11]和Yang等[12]分别将学习效应和遗忘效应引入生产调度领域。赵静等[13]应用改进萤火虫算法求解具有学习退化效应的阻塞流水车间调度问题，研究表明最大完工时间随学习效应的增强而缩短，随退化效应的增强而延长。Chiu[14]建立了具有学习退化效应的批处理加工模型，研究表明了大批量加工的必要性。侯丰龙等[15]运用布谷鸟算法，求解同时具有学习遗忘效应的TFTLCD模块组装调度问题，结果表明设备调整时间在大批量生产过程中将严重影响工件加工效率。目前学者在生产调度研究中较少综合考虑退化效应。

本文将学习退化效应引入TFT-LCD面板成盒调度问题，研究具有学习退化效应的TFT-LCD面板成盒多目标调度问题中，运用新型智能算法求得帕累托非劣解集，分析不同学习率和退化因子对调度结果的影响，使研究对象的模拟生产环境更为贴近现实。

2 模型描述

2.1 TFT-LCD单元装配过程描述

TFT-LCD生产包括3大制程：阵列制造（Array）、面板成盒（Cell）和模块组装（Module）。在 Array 阶段，玻璃基板经过几轮洗净、成膜、光阻剂涂敷、曝光、显影、刻蚀和去光阻的多重入操作，形成TFT和电极阵列，检验合格后，进入下一个加工阶段。在Cell阶段，将不同规格的TFT玻璃基板与彩色滤光片（C/F）进行贴合，切割成为面板后，加上偏光板，现场生产情况如图1所示。在Module阶段，将LCD与客户定制的部件，包括集成电路（IC）、印刷电路板（PCB）、驱动板、背光源和底盘组装为最终产品。

图1 TFT-LCD cell阶段生产实况Fig.1 TFT-LCD cell stage production actual scene

TFT-LCD的Cell阶段属于并联式的混合流水装配作业。两组清洗后的零件在完成各自固定加工流程后进行组装。Cell阶段工艺流程如图2 所示。

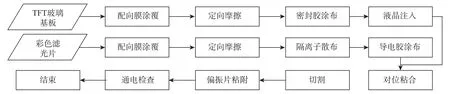
图2 Cell阶段工艺流程图Fig.2 Cell stage process flow chart

2.2 具有学习退化效应的面板成盒多目标调度模型

加工等待时间相关的学习退化效应模型，工序Oij在机器m的第v个位置上的实际加工时间为pirm，如式（1）所示。

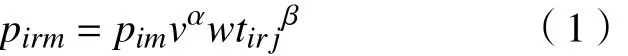
面板成盒调度是在约束条件的限制下，通过分配工件工序的加工机器及加工机器上待加工工件的加工顺序，达到优化调度各目标的目的。在调度中满足如下假设：

a. 每台机器某一时刻只能加工一批工件（装配工序中，零件A，B合并为一批工件C）；

b. 每批工件某一时刻只能被一台机器加工；

c. 零件A，B及装配后工件的加工路径确定；

d. 每批工序加工时间由产品类型及加工机器性能预先确定；

e. 工序一旦开始加工，加工过程中不允许中断。

2.2.3 数学模型建立

本文设立3个以最小化为优化方向的目标函数：最大完成时间Cmax、总机器空闲时间Twait和工件加权延期时间Ttard-w。其函数公式为

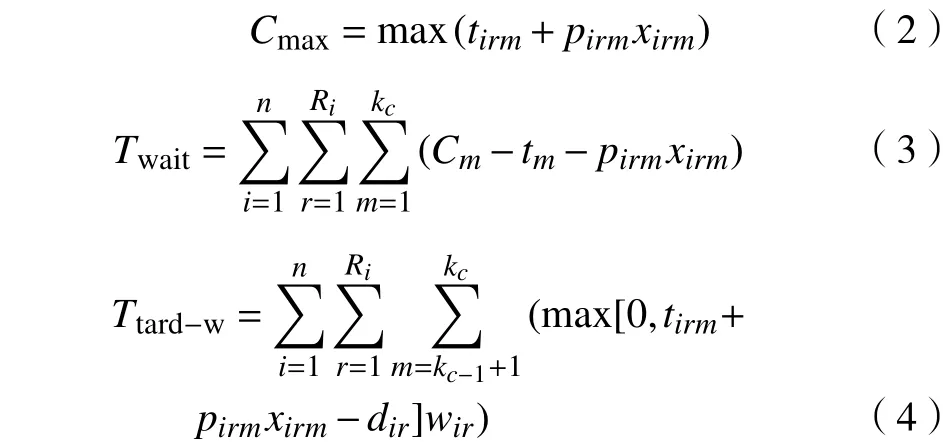
式（3）中，Cm表示机器m完成加工最后一个工件的时间，tm表示机器m开始加工第一个工件的时间。

约束条件为

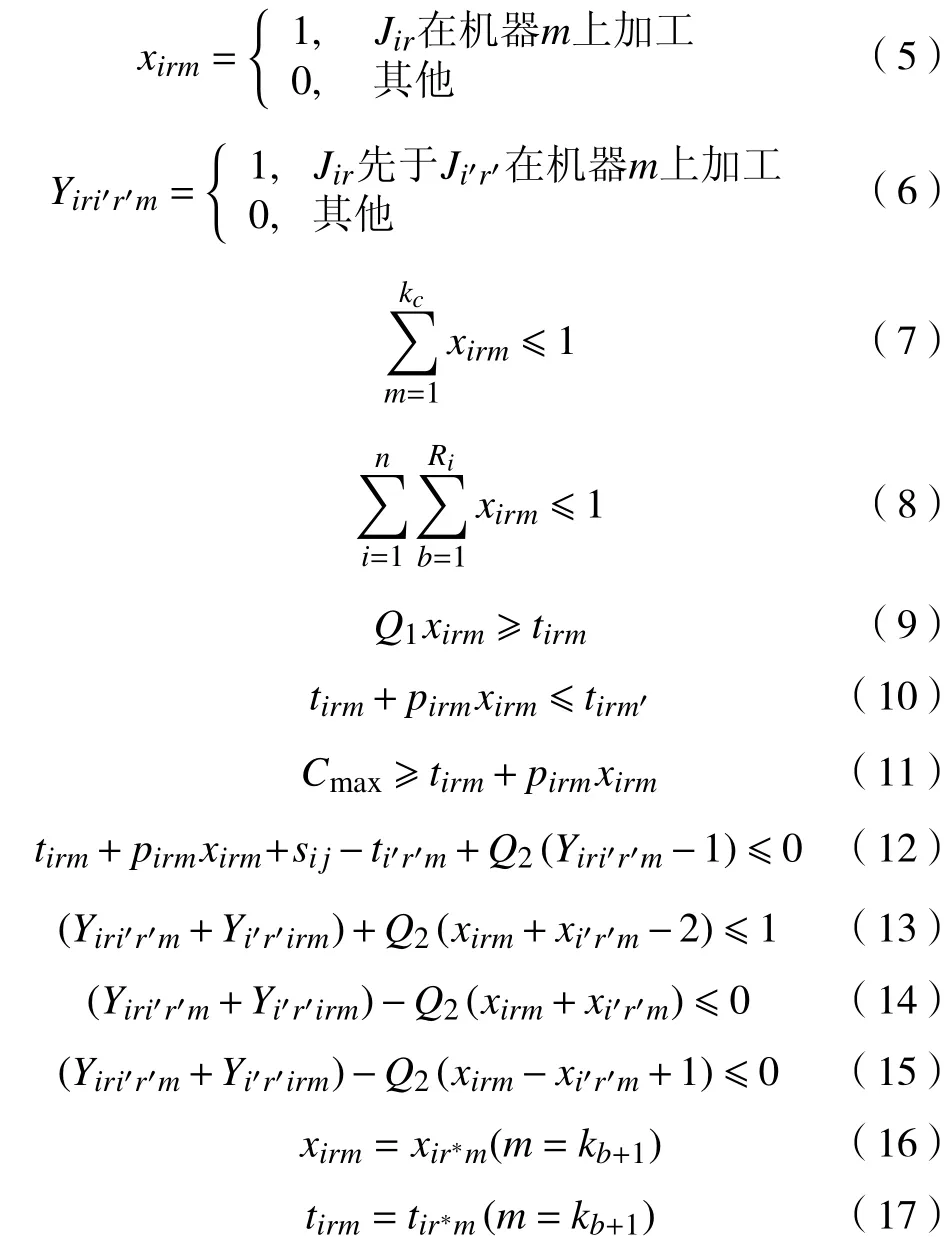
式中，Q1，Q2为无穷大正数，xirm与为决策变量。式（7）表示一批工件同一时刻至多只能在一台机器上加工；式（8）表示一台机器同一时刻至多只能加工一批工件；式（9）中，当xirm=0时，tirm0，即工件在该台机器上加工时，具有对应开始加工时间；式（10）表示工件严格按照工序加工路径进行加工，式中的m，m'表示一批工件前后两个工序的加工机器；式（11）表示最大完工时间约束；式（12）表示一台机器上先后邻加工工件批的开始加工时间约束；式（13）～(15)表示同一台机器上加工的工件批序列关系约束；式（16）～（17）表示装配工序中，原料A，B在同一台机器上同时开始加工。

3 多目标布谷鸟算法

3.1 算法仿生原理

布谷鸟搜索算法（cuckoo search，CS）由模拟布谷鸟寻窝寄生育雏的方式启发而来。布谷鸟自身不筑巢不孵卵，而由宿主鸟代为孵化。为了增加自身鸟蛋的存活概率，布谷鸟选择与自身孵化过程相似的宿主鸟巢，趁宿主外出时，在其鸟巢中产一枚蛋，并移除一枚宿主的鸟蛋。在此过程中，若宿主发现被占巢，会选择扔掉布谷鸟蛋或放弃被占鸟巢另筑新巢。

3.2 算法描述

为了通过模拟布谷鸟寻窝过程，解决多维空间寻优问题，需要设立以下3点理想假设：a. 一只布谷鸟每次只产一枚蛋，并随机选择宿主鸟巢；b.最好的鸟巢将直接保留到下一代；c. 可用宿主鸟巢数量n固定，宿主发现布谷鸟蛋的概率为[0，1]，而被发现的布谷鸟需要寻找新的宿主巢。在以上假设基础上，布谷鸟寻窝的路径和位置更新公式为

3.3 构建帕累托非劣解集

在多目标规划问题中，需要同时考虑多个目标的最优化，当各目标之间存在冲突时，通过构建帕累托非劣解集，解决多目标规划问题在寻优过程中个体目标值的分配问题[16]。帕累托非劣解是指：在方案集合K中，对于某一方案x，存在另一个方案y，使得方案x对应的所有目标函数值皆不劣于方案y对应的目标函数值，且存在至少一个y对应的目标函数值劣于x对应的目标函数值，则称x支配y，记为， 若集合K中不存在其他方案支配x，则x为此问题的一个帕累托非劣解。

本文通过结合双元锦标赛与动态淘汰制方法，构建帕累托非劣解集。实现过程为：选择当代鸟巢集合K中的第一个方案x，将其与剩余方案集Q中的各方案进行第一轮比较；若剩余方案集Q中存在方案被x支配，则从K中删除该被支配方案；第一轮比较完成时，若Q中方案均不支配x，则添加x至帕累托非劣解集P，从集合K中删除x；若Q中存在方案支配x，则从集合K中删除x，依此类推，直至K为空集；若解集P规模超过预定数，则依据聚集距离进行筛选；若已有集合P，则需将两代帕累托非劣解集合并，进行第二轮比较。通过在每轮循环中淘汰被支配解，缩小方案集合K的规模，可有效降低算法复杂度。算法具体步骤如下：

a. 选定集合K中的比较方案x；

b. 令剩余集合Q=K-x，被支配解集Rx=ϕ，支配解集Zx=ϕ；

c. 依次比较x与Q中各方案，判断支配关系，求出解集Rx，Zx；

d. 令 K=K-Rx， 若 Zx=ϕ， 则 令 P=P∪{x}，K=K-x；若 Zx≠ϕ，则令 K=K-x；

e. 当|K|＞1，转步骤 a，否则令 P=P∪K；

f. 若集合P规模大于预定数，依据聚焦距离降序选取，否则转步骤g；

g. 若不存在已有P，则退出，否则K=P*，返回执行步骤a～f。

3.4 多目标布谷鸟算法步骤描述

布谷鸟算法迭代步长采用莱维飞行，行走步长满足一个重尾（heavy-tailed）的稳定分布，兼具短距离探索和偶尔较长距离行走，能有效扩大搜索范围，增加种群多样性，更容易跳出局部最优点。结合双元锦标赛、动态淘汰制与聚焦距离筛选方法，多目标布谷鸟算法流程如图3所示。

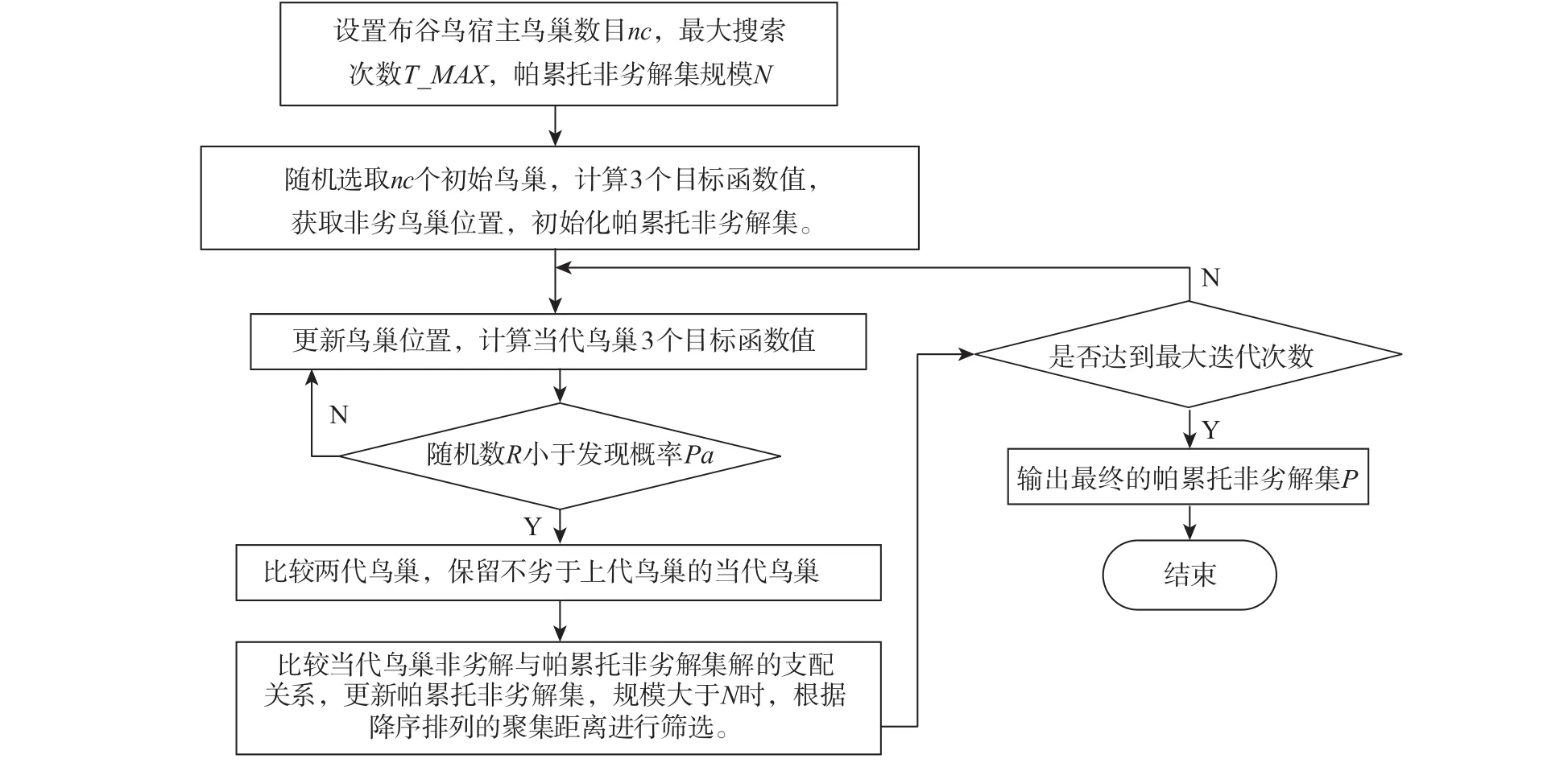
图3 多目标布谷鸟算法流程图Fig.3 Multi-objective cuckoo algorithm flow chart

4 基于多目标布谷鸟算法的TFT-LCD面板成盒多目标调度研究

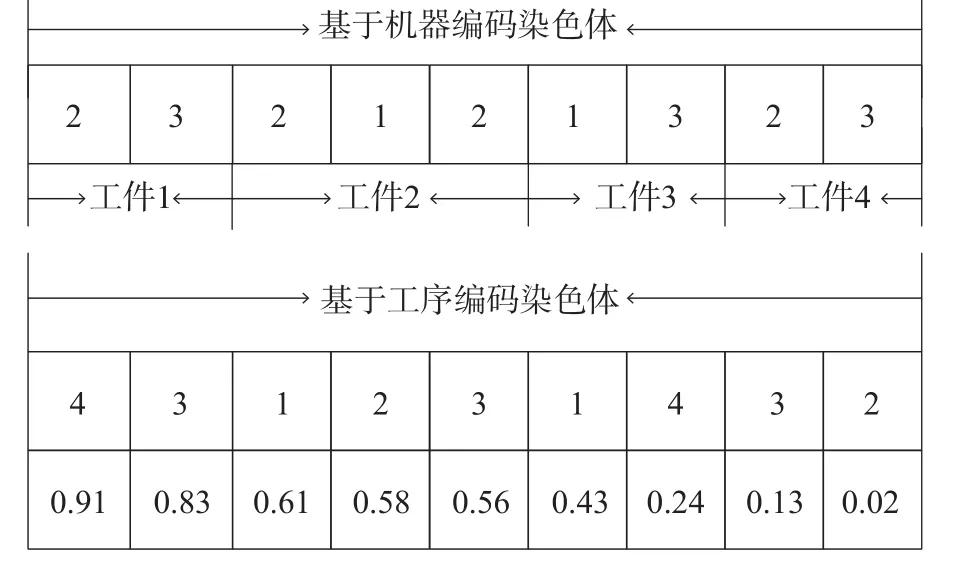
图4 两段式编码方式Fig. 4 Two segment encoding method

4.1 TFT-LCD面板成盒问题编码

TFT-LCD面板成盒调度需要同时分配加工工件每道工序的机器和工件在机器上加工的顺序。针对TFT-LCD模块组装调度的这一特性，本文设计基于工序和机器相结合的两段式编码方式。同时，鉴于算法的迭代求解特性，基于工序编码染色体采用李永林等[17]提出的IMM编码方式，如图4所示。

图4中，基于机器编码的染色体中，表示的机器依次为{M12,M13,M22,M21,M22,M31,M33,M42,M43}。基于工序编码染色体中，上行为工件编号，框中的数字表示工件的标号，出现频次表示工件的工序数，下行为降序排列的随机数或布谷鸟迭代后数据，表示的工序依次为{O41,O31,O11,O21,O32,O12,O42,O33,O22}。第一条染色体由工序对应加工机器数确定工件工序的加工机器，第二条染色体借由随机实数序列降序排列，确定工件工序的加工顺序，确保调度解可行。

4.2 多目标布谷鸟算法实验论证

为了验证上文算法在解决TFT-LCD面板成盒多目标调度问题时的有效性，现以文献[7]中某车间的实际生产数据为例，对具有加工准备时间的TFTLCD面板成盒调度问题（11道工序）进行实验对比。工件类型及批量数如 表1所示，各工序机器数如 表2所示，工件类型批次对应交货期、加权延迟如表3所示；加工类型变换时，工序所需准备时间如表4所示；工序对应的机器加工时间如表5所示。

表1 工件类型及批量数Tab.1 Work-piece type and lot size

表2 各工序机器数Tab.2 Machine numbers in each process

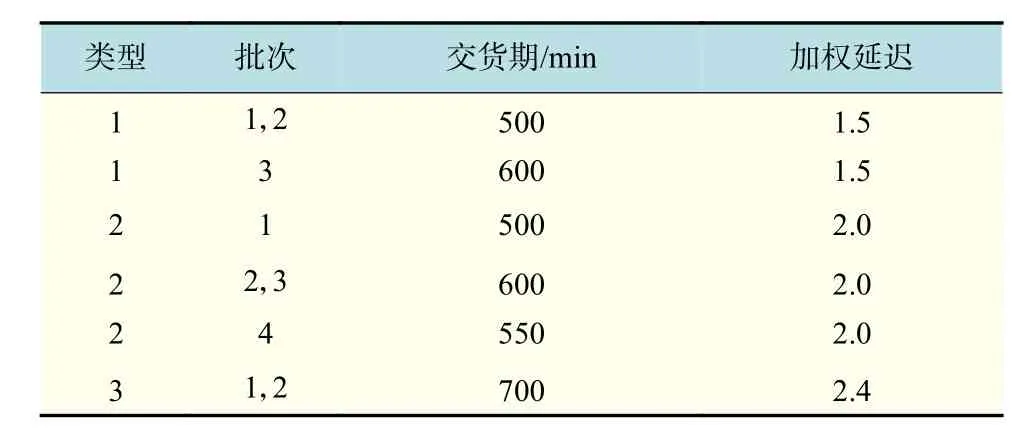
表3 工件基本信息Tab.3 Work-piece basic information

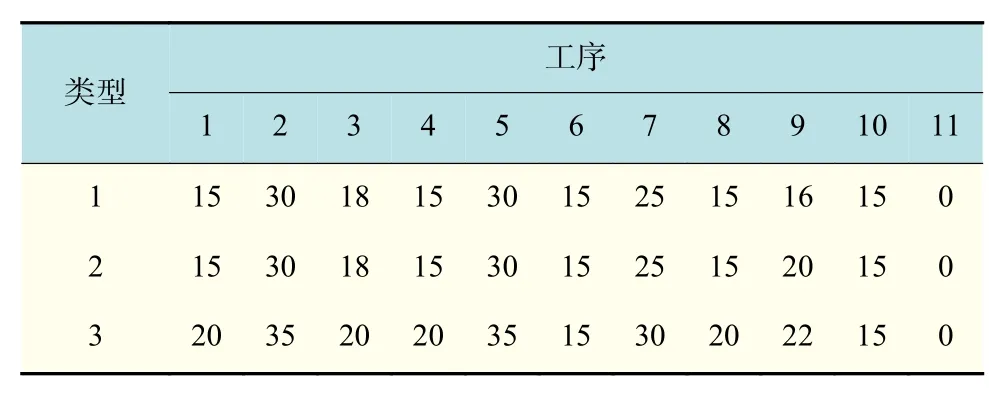
表4 加工工件类型更换时所处工序准备时间Tab.4 Process setup time when the work-piece type is changed min

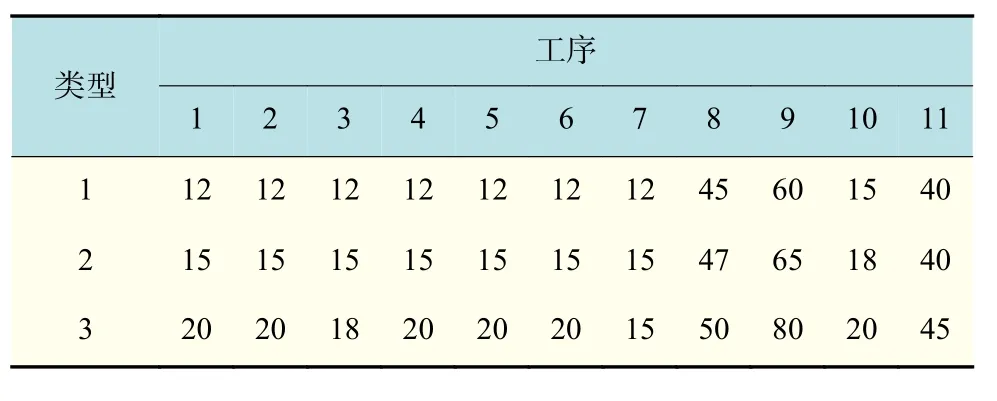
表5 工序对应机器加工时间Tab.5 Machine processing time min

面板成盒调度问题算法仿真实验环境为：Windows 8 操 作 系 统 ，CPU 为 Intel(R) Core(TM)i7-4720HQ，处理器主频为 2.60 GHz，8 G 内存，编程环境为 Matlab R2014b。

应用本文的多目标布谷鸟算法，对问题进行求解。初始设置与文献[7 ]匹配，初始种群规模、迭代次数分别为50，100，算法中步长因子前系数取值0.1（源代码解决连续函数问题时，取值0.01），以最大完成时间与f=0.5Cmax+0.5Ttard−w为目标函数。独立运行10次，与文献[7]中静态解码（SD）、静态解码–精英保留（SD-ES）、贪婪解码（GD）、贪婪解码–精英保留（GD-ES）4种遗传算法及文献[18]中ELFT（工序期望最短完成时间）规则进行比较，结果如表6和下页表7所示。

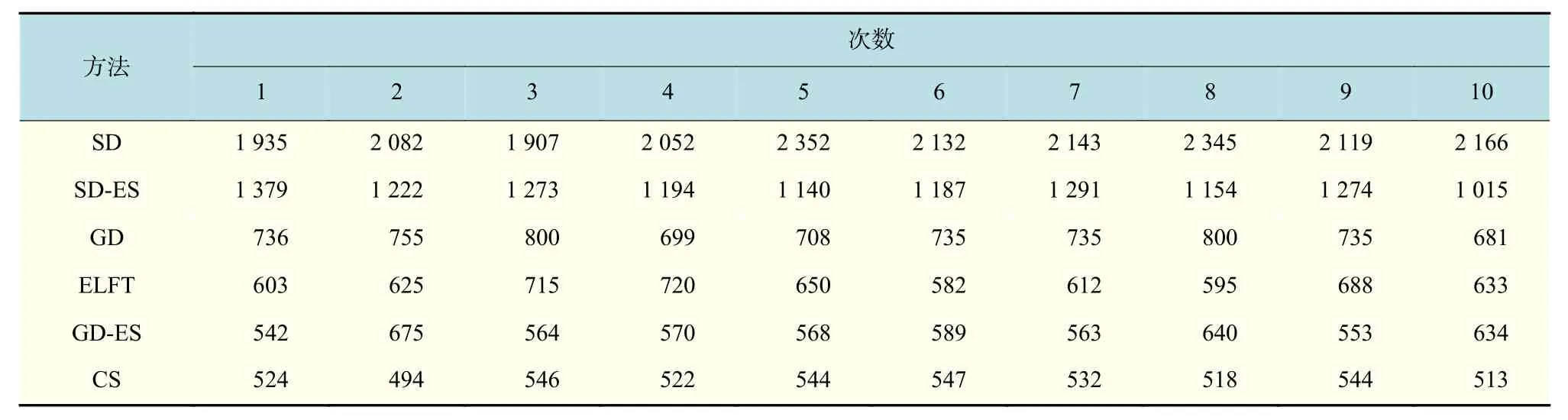
表6 6种方法得到的最大完成时间Tab.6 Cmax obtained by six methods min

表7 6种方法得到的两项加权目标函数最优值Tab.7 Min f obtained by six methods min

从表6和表7可知，在Cell阶段整体调度问题中，布谷鸟算法优于其他5种算法。取其中结果较优的3种算法，10次结果取平均值、最小值，并计算标准差，结果如表8所示。

多目标布谷鸟算法相比较其他5种算法中最优的贪婪解码–精英保留遗传算法，求解出的最大完成时间及加权目标函数平均值优异性分别提升10.4%，6.5%，最大完成时间及加权目标函数最小值也各自降低了8.6%，11.2%，且求得解的平均标准差最小，算法稳定性较高。

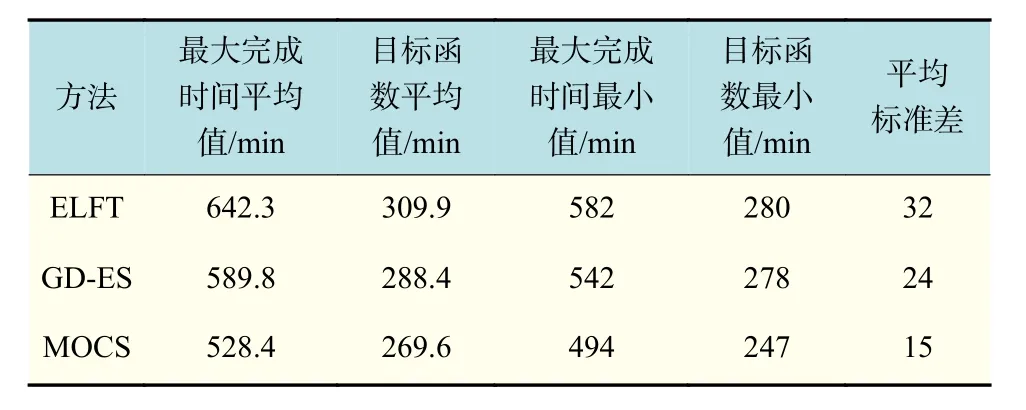
表8 3种方法结果对比Tab.8 Comparison of three methods results

4.3 TFT-LCD面板成盒多目标调度实验应用

在实际生产过程中，机器加工时间除了与加工工件类型有关，也常由机器本身性能决定。针对这一生产特性，结合前文提出的具有12道工序的Cell阶段制程，对前节实例作出部分修改。工序机器数如表9所示，加工类型变换时，工序准备时间如表10所示，工序对应的机器具体加工时间如表11所示。

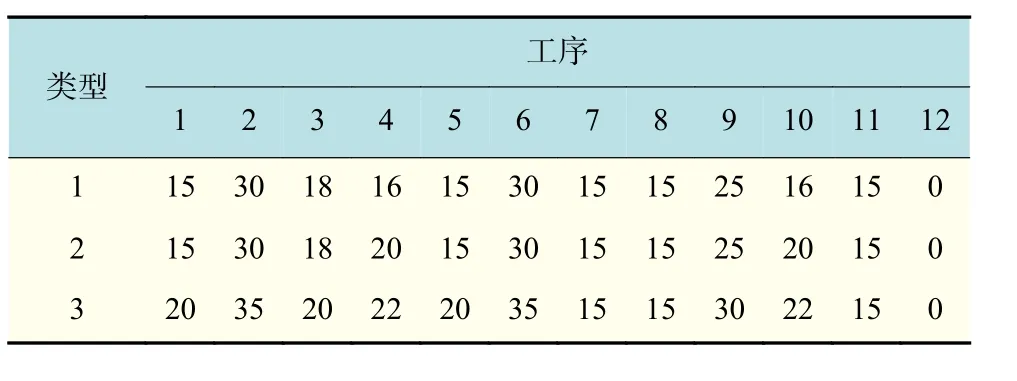
表10 加工工件类型更换时所处工序对应准备时间Tab.10 Process setup time when the work-piece type is changed min

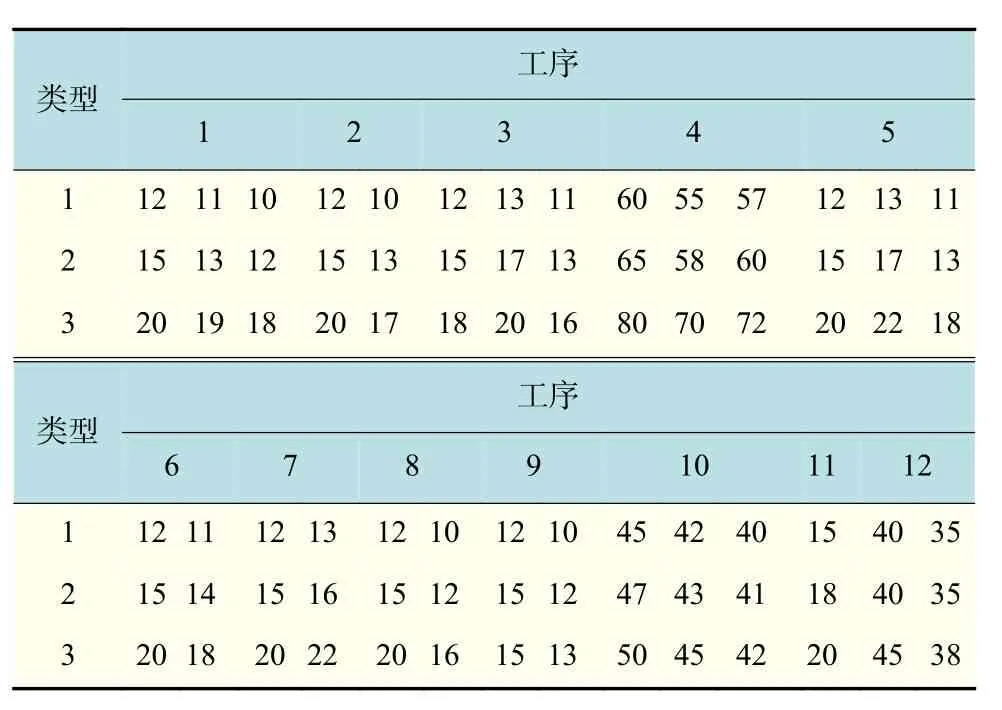
表11 工序对应机器加工时间Tab.11 Machine processing time min

运用多目标布谷鸟算法求解该问题，独立运行10次后，得到的帕累托非劣解集的3个目标函数均值分别为598，71，154。每组帕累托非劣解中皆包含加权延期时间最小值0，且可求得不大于10的机器空闲时间。表12是独立运行3次，多目标布谷鸟算法在求解该问题时得到的帕累托非劣解集。

本文3个目标值均以最小化为方向。对比第一次运行第一、第八组解，可以发现Cmax不到1%的降低，升高了37.5%的Twait。虽然离第一目标的值很接近，但由于两个解3个目标值的总距离较大，依据聚集距离密度评价指标筛选时，择其一的发生概率较小。由此可见，人工决策在最终多目标方案决策中的重要性。图5是3组非劣解集绘制成的三维图及其3张拆分二维图。

从图5二维图中可以发现，最大完工时间与加权延迟时间正相关，而机器空闲时间与最大完工时间、加权延迟时间负相关。独立运行10次，取得95个帕累托非劣解，通过数值统计得到：最大完工时间与加权延迟时间相关系数为0.88，机器空闲时间与最大完工时间、加权延迟时间相关系数分别为–0.78，–0.53，呈高度相关及显著性相关关系。显著性（双侧）皆为0.00，通过Pearson相关性检验。

表12 多目标布谷鸟算法求出的3组帕累托非劣解集Tab.12 Three Pareto sets obtained by the multiobjective cuckoo algorithm min

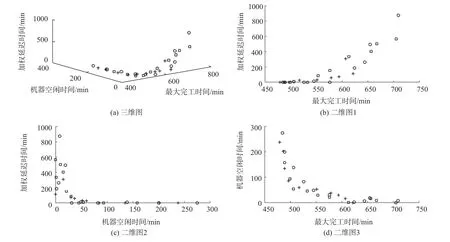
图5 3组帕累托非劣解集的三维图及二维图Fig.5 3D graph and 2D graphs of three Pareto sets

5 具有学习退化效应的TFT-LCD面板成盒调度研究

根据前文提出的学习退化效应模型，建立具有学习退化效应的面板成盒多目标调度模型。以最小化最大完成时间Cmax、机器空闲时间Twait、加权延误时间Ttard-w为目标函数，采用上文描述的多目标布谷鸟算法求解前文实际生产数据。不同学习率及退化因子下独立运行40次，分别得到的帕累托非劣解集3目标函数平均值如表13和下页表14～15所示，解的个数情况如下页表16所示。

表13 不同学习率及退化因子影响下帕累托非劣解集的最大完成时间平均值Tab.13 Cmax mean of Pareto sets under different learning rates and degradation factors min

表14 不同学习率及退化因子影响下帕累托非劣解集的机器空闲时间平均值Tab.14 Twait mean of Pareto sets under different learning rates and degradation factors min

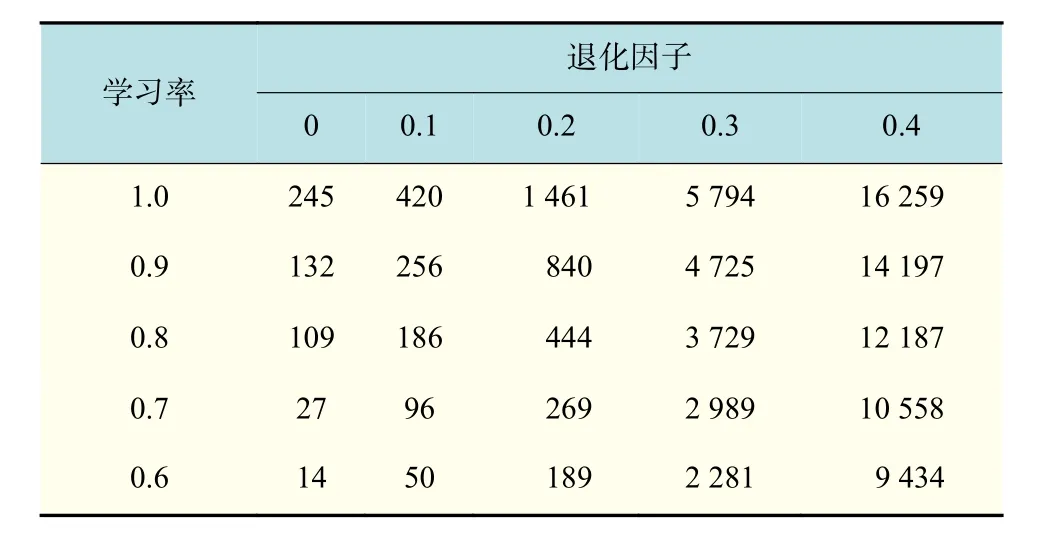
表15 不同学习率及退化因子影响下帕累托非劣解集的加权延迟时间平均值Tab.15 Ttard-w mean of Pareto sets under different learning rates and degradation factors min

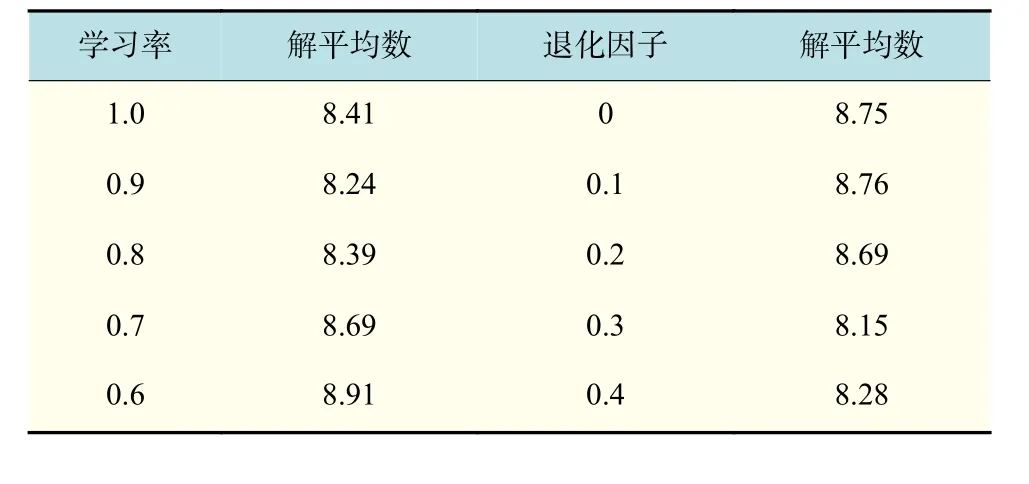
表16 不同学习率及退化因子影响下帕累托非劣解集平均个数Tab.16 Average number of Pareto sets under different learning rates and degradation factors

从表16可以看到，学习率及退化因子的变化对解个数影响不显著。为便于直观分析，不同学习率及退化因子下的帕累托非劣解集目标函数平均值如图6～8所示。

图8中，因数值跨度较大，仅展示部分数值点。表13～15数据表明：同一学习率l条件下，最大完成时间及加权延迟时间平均值随退化因子b的变大而升高，且b=0.2为该两项目标平均值退化效应的临界点，当b＞0.2时，该两项平均值增幅明显变大（加权延误时间平均值在b＞0.2时，呈指数型增长，数值较大，为清晰显示趋势，图中省略）。而当b相同时，最大完成时间及加权延误时间平均值将随着l的减小，即学习效应因子的变大而降低。以上数据与实际生产情况相符，工人或机器的学习能力越强，完成一批工件的时间将被缩短，按时交货能力提高。而b的增加意味着退化效应的增强会削弱工件加工的效率，拉长生产周期，削弱按时交货能力。机器空闲时间在b＞0.2时，随学习效应增强，目标值上升较为显著，b=0.2时，上升缓慢。而在b＜0.2的情况下，目标值下降后现回升或持平趋势。

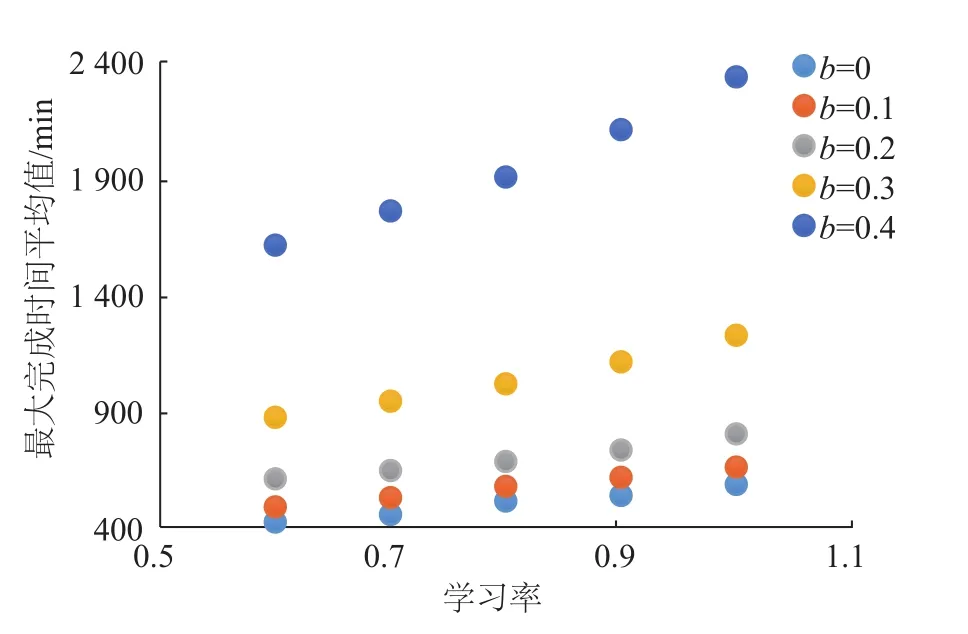
图6 不同学习率及退化因子影响下帕累托非劣解集的最大完成时间平均值Fig.6 Cmax mean of Pareto sets under different learning rates and degradation factors

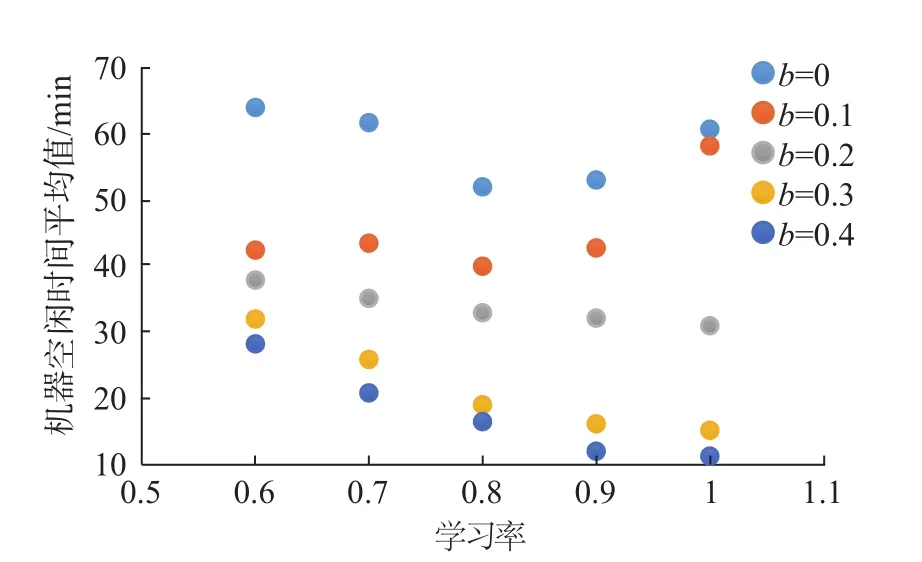
图7 不同学习率及退化因子影响下帕累托非劣解集的机器空闲时间平均值Fig.7 Twait mean of Pareto sets under different learning rates and degradation factors

下面引入敏感性分析，研究不同学习率和退化因子变化下，工件最大完工时间、机器空闲时间和交货加权延误时间3个目标值的变化情况，用敏感度系数表示，如式（20）[19]所示。

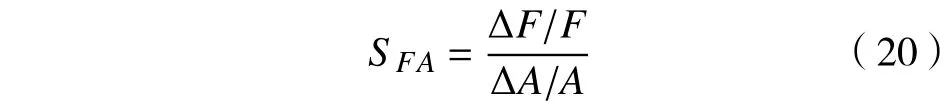
式中：SFA代表模型目标值F对于因素变量A的敏感程度；∆A/A表示因素变量变化率；∆F/F表示不同因素变化量情况下，目标值的变化率。不同学习效应及退化因子影响下，最大完成时间及加权延误时间、机器空闲时间平均值敏感度系数如表17所示。

图8 不同学习率及退化因子影响下帕累托非劣解集的加权延迟时间平均值Fig.8 Ttard-w mean of Pareto sets under different learning rates and degradation factors

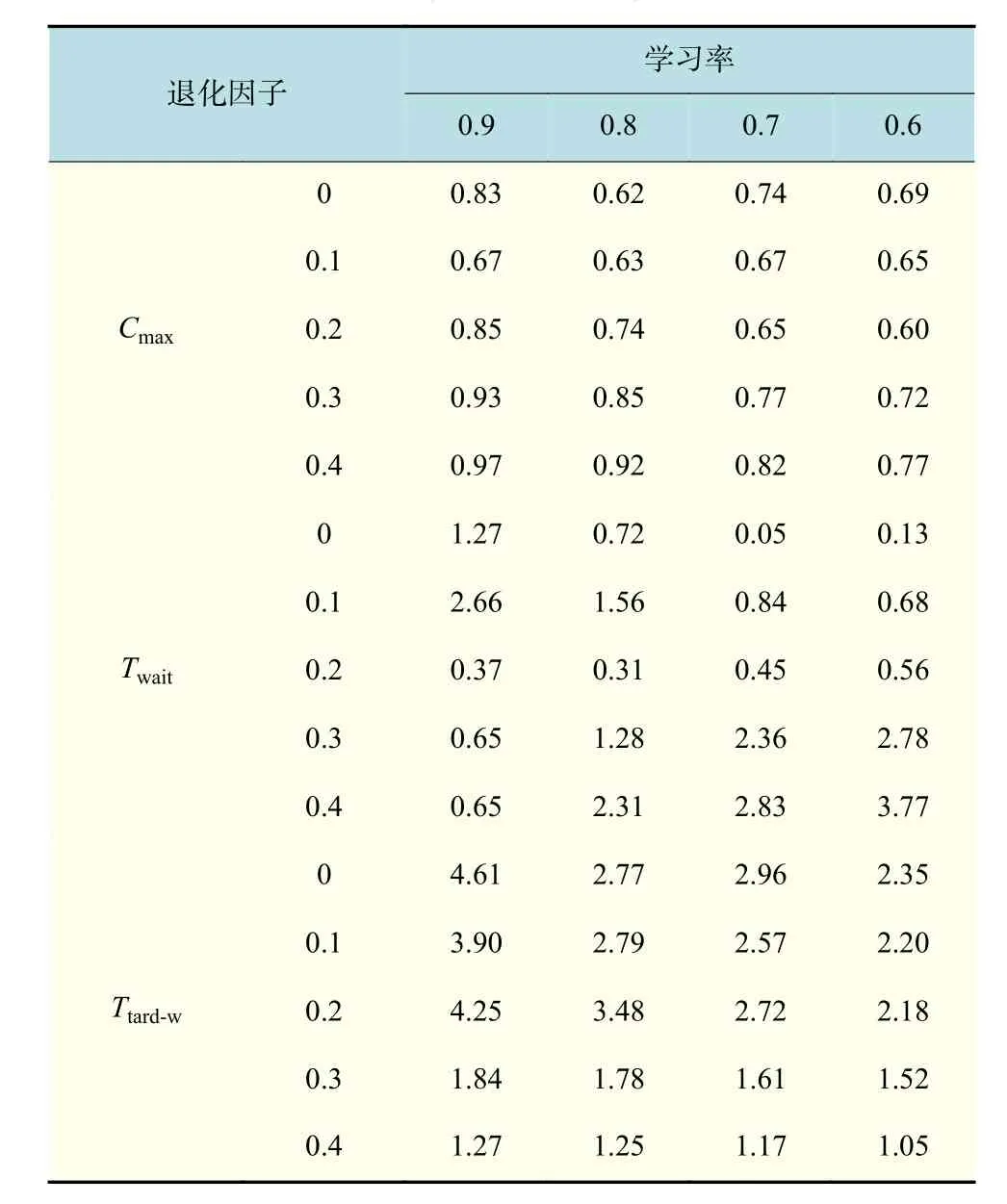
表17 不同学习率及退化因子影响下目标平均值敏感度系数Tab.17 Sensitivity coefficient of the target mean under different learning rates and degradation factors

由表17可知，从数值来看，Cmax对学习及退化因子的敏感度较低，另两项敏感度较高。从横向趋势来看，Cmax及Ttard-w敏感度随学习效应的增强而降低，Twait敏感度则相反。从纵向趋势来看，Cmax的敏感度系数随退化效应的增强小幅度下降后上升，Twait的敏感度系数上升回落后再大幅上升，Ttard-w敏感度系数小幅跌落回升后大幅度下降。学习效应对目标值的影响较为平稳，而退化效应在不同学习效应情况下，对不同目标的作用力大小不尽相同。在实际生产活动中，要严格控制退化因素，合理安排规模调度，定期检查和维护机器设备。

6 结论与展望

TFT-LCD 行业竞争环境激烈，产品寿命周期较短，通过合理优化调度，缩短工件加工时间，充分利用机器，提高按时交货率，将对生产实践产生积极影响。本文从具有学习退化效应的多目标优化角度切入，建立TFT-LCD面板成盒调度模型，并应用改进后的多目标布谷鸟算法进行求解，实验结果发现，最大完成时间与加权延迟时间正相关，与机器空闲时间负相关。加入不同学习及退化效应后，分析目标值的敏感度系数发现，学习效应对生产活动的影响平稳，而退化效应应被重视，尽力降到最低。关于具有学习退化效应的TFT-LCD多目标优化研究才刚刚起步，本文的研究在理论和现实中都具有一定的意义。但是，相关研究也需要立足于实际生产、服务于实际生产，这也将是一个需要不断努力和探索的漫长过程。作者将继续研究具有不同行为效应的TFT-LCD调度问题，使研究内容更贴近实际生产情况。