基于EFAST的在线极限学习机节点剪枝方法

（福州理工学院，福建 福州，350002）

极限学习机（extreme learning machine，ELM）[1-3]是在单隐藏层网络结构基础上新近发展的机器学习技术，有处理快速、泛化精度高、结构简单等优点，但这种标准的极限学习机并不能在学习的同时也能对自身的网络结构进行自适应调整，给极限学习机带来了一定的局限性，并且当隐藏节点过多时会导致ELM的过拟合的问题，反之过少的时候，则会导致ELM泛化精度降低。目前极限学习机的网络结构自适应调整方法总体上分为3类：剪枝方法，增长方法，混合方法。P-ELM[4]、OP-ELM[5]、ImSAP-ELM[6]和SVM-ELM[7]是属于剪枝的方法，一般会初始化一个较大的单隐藏层网络结构，再按照一定的标准，对隐藏层中各个节点的重要性进行分析，最后舍去非重要的节点从而达到对网络结构的优化，但这些方法只能是单纯对节点个数进行优化，并且无法应用于在线的极限学习机（OSELM）。I-ELM[8]和CEOS-ELM[9]。是属于增长的方法，会从一个初始较小的网络，然后逐步添加节点，一直到网络的精度满足期望的要求，在训练时，一般需要指定最高的训练精度与最大的网络规模，但这两个参数在实际当中是难以预先估计。EOS-ELM[10]、VS-OSELM[11]和HOS-ELM[12]是属于混合的方法，这类方法既有添加节点功能也包含节点删除的功能，在实际中实现相对复杂，所需设置参数较多，因而增加了ELM的使用难度。

本文的方法属于一种剪枝类方法，首先通过使用扩展的傅里叶振幅敏感度测试（EFAST）[13-15]对OS-ELM的隐藏层各节点进行敏感度分析，能更加准确的分析各个隐藏节点对网络输出的重要性，从而能准确的去除网络中非必要的节点，并且设计了一种基于迭代最小二乘法的参数调整方法，可以对剪枝后的OS-ELM参数进行调整，从而达到优化网络结构的目的，最终在公开的数据集上验证了方法的有效性。

1 OS-ELM与EFAST

1.1 OS-ELM

在线极限学习机是一种单隐藏层神经网络结构，它利用迭代的最小二乘法 （recursive least square，RLS）能实时的调整网络的权值。如图 1所示的OS-ELM有h个隐藏层节点和m个输出层节点。对于OS-ELM它有一个初始化的过程，需要使用N0个输入样本对输出层的权值进行初始化，之后当有新的训练样本到时，OSELM会通过新来的训练样本计算输出层的参数，它的算法具体的实现如下：

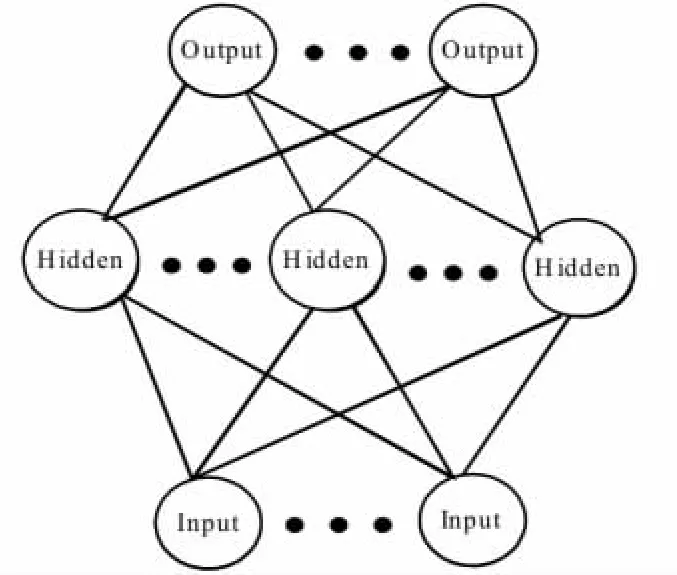
图1 OS-ELM基本结构

（1）选取激励函数f，采用随机过程生成h个输入层的映射向量W和偏置值B。

（2）OS-ELM网络的初始化过程，需要利用输入的N0个样本得到隐藏层输出矩阵H0和标记矩阵T0，求解初始化的迭代更新量k0=H0TH0和输出层β0=k0H0TT0。

（3）对于第i批次输入的训练样本，通过f、W和B可计算得相应的隐藏层输出矩阵Hi和标记矩阵Ti，那么第i次训练得到的输出层参数βi与迭代更新量ki可递归地表示为：

1.2 OS-ELM的傅立叶振幅敏感度测试

EFAS是用来检测系统各个输入量对系统的总体输出方差的影响，其本质的思想是当一个输入量对系统总体输出方差产生的影响越大，那么输入量对整个输出的影响就越大，该输入在系统中的重要性就越大。如果把OS-ELM结构分成输入层到隐藏层和隐藏层到输出层两个部分。第一部分使用随机映射方式，把输入空间的向量随机映射到OS-ELM的特征空间。第二部分由于隐藏层的输出与系统输出的关系可以描述为函数：

该函数可以用傅里叶级数展开如式（4）：

其中Aj和Bj可以如下表示：

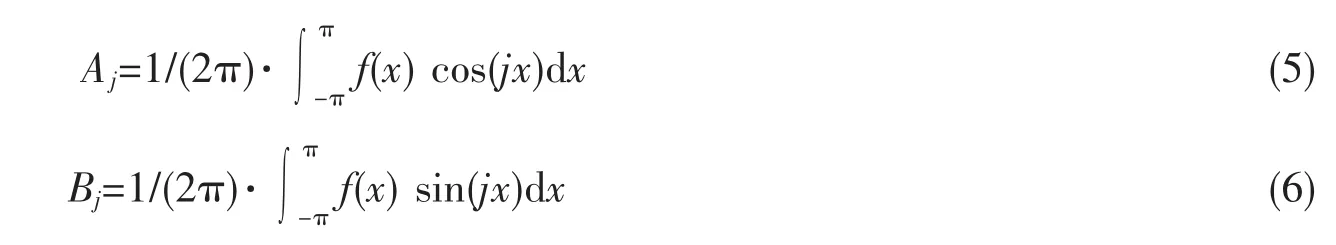
对于准确衡量输入zi对总体输出的影响，EFAST通过计算公式 (7)描述输入zi对总体输出的影响。

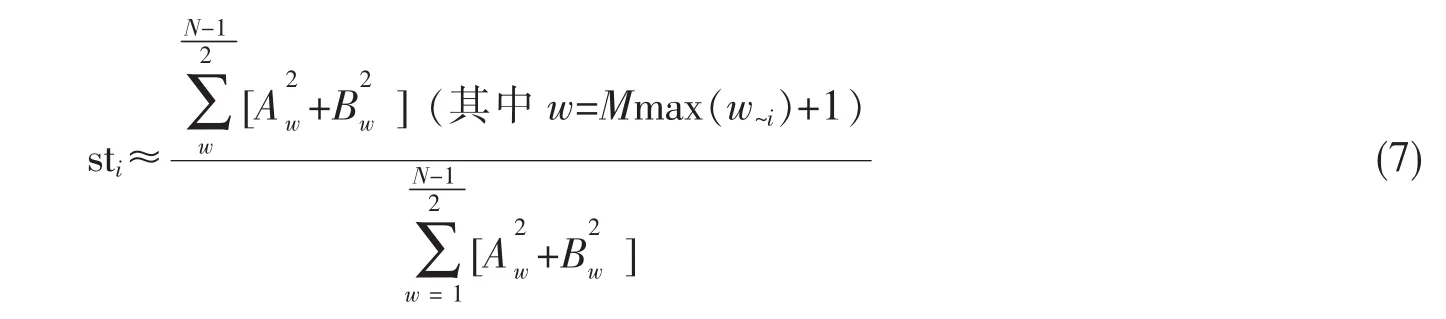
这里M为敏感分析系统的干扰因素（一般设为4或6）。其中w～i表示输入z～i=zi,z2，…zi-1,zi+1,…,zh的频率值，当要计算sti时，就把zi频率设置为wi=max(wk=1,2,…，h)。同时也需要满足下面的两个等式：

2 FOS-ELM模型

2.1 FOS-ELM的网络参数调整方法

当利用FAST算法对OS-ELM的节点敏感度分析，对网络结构进行剪枝优化后，需要重新调整OSELM权值，基于标准的OS-ELM算法，本文设计了一种对剪枝后权值进行调整的算法。假设OS-ELM通过第n-1批样本训练，得到的输出层参数为β0，迭代更新量为k0。对于第n批的训练样本，通过EFAST敏感度测对各个隐藏层节点进行分析，删除网络中敏感度低于指定阈值的节点(不失一般性，假设被删除节点编号是{1,2,3..，t})，并且定义为隐藏层输出矩阵H0删除第{1,2,3,t}列向量得到的矩阵：

与OS-ELM一样，需要求解剪枝后的输出权值β1和迭代更新量k1，对于在线的OS-ELM学习算法，需要将 β1表示为的函数：

在式(12)中，

其中k1和β1分别可以表示为：

2.2 FOS-ELM的隐藏节点剪枝方法

选取一个含足够多个隐藏层节点的单隐藏层神经网络作为FOS-ELM的初始结构，选取隐藏层节点激活函数f，并随机生成输入层的权值W和隐藏层节点的偏置值B来进行初始化网络，并且计算输出层的初始化权值β0和 k0，对于接下来每一批次的样本数据，首先利用傅里叶振幅测试，对隐藏层节点的敏感度进行计算，当节点的敏感度小于阈值δ时，就从当前的网络中移除该节点，然后并通过本文中设计的权值调整方法来调整结构优化后的OS-ELM的输出层权值βi与迭代更新量ki。具体的FOS-ELM剪枝的流程。

3 实验结果分析

为了验证设计的FOS-ELM算法在优化网络结构上的有效性，在以下5组数据进行对比实验比较。

（1）论文[13]实验数据：5000个训练样本，5000个测试样本，每个样本有4个输入属性和1个输出属性。（2）Concrete compressive strength数据：来自于UCI数据库，730条训练样本，300条测试样本。每条样本有8个输入属性和一个输出属性。（3）Diabetes数据：来自于ELM官网提供的数据。576条训练样本，192条测试样本，8个输入属性，2个输出类别。（4）Landsat satellite image数据：来自于ELM官网提供的数据。4435条训练样本，2000条测试样本，36个输入属性，6个输出类别。（5）Segment数据：数据来自于ELM官网提供的数据。1500条训练样本，810条测试样本，19个输入属性,7个输出类别。

实验结果见表1～6。

表1 函数16的测试结果

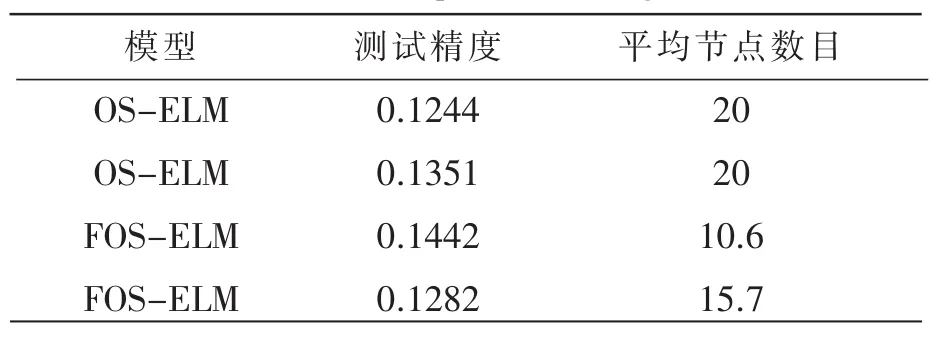
表2 Concrete compressive strength的测试结果

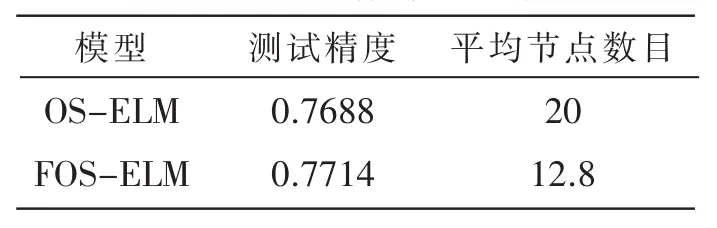
表3 Diabetes数据测试结果

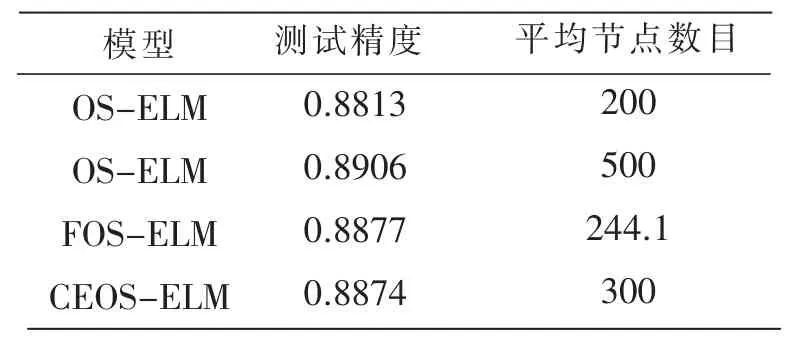
表4 Satellite Image数据测试结果

由表 1～2的数据，提出的FOS-ELM方法在保证回归精度的条件下，所使用的节点的数目均少于标准OS-ELM和HOS-ELM。同样在表 3～5中，在保证泛化精度的条件下，FOS-ELM的使用的隐藏节点数目均少于CEOS-ELM和OS-ELM，

4 结论

由于OS-ELM不能自适应调整网络结构的问题，设计了一种基于EFAST的隐藏层节点剪枝算法（FOS-ELM），利用傅里叶敏感度测试方法对OS-ELM的隐藏节点分析，能适用于剪枝后的网络参数调整算法，最后也通过实验验证了所设计算法的有效性。目前，本文的剪枝方法只应用于单隐藏层的在线极限学习机上，后续的研究工作可以从多隐藏层极限学习机的剪枝方法上展开；在模型复杂度欠缺情况下，极限学习模型如何有效的增长也是个有待解决的问题。