基于模糊综合评价的新型折叠自行车优化设计

（三明学院 机电工程学院，福建 三明 365004）

由于国民经济的发展，摩托车、小汽车等交通工具急剧增加，导致环境污染与交通拥挤等问题的出现。目前，环保问题是国家和人们非常关注的焦点，因此自行车出行不仅低碳环保，而且有益身心健康，是人们短途出行的重要交通工具[1-3]。

但是目前普通自行车都具有体积大、质量大等缺点，不方便骑行者使用与停放[4-5]，因此折叠自行车成为了人们青睐的对象。国内外有些学者已对折叠自行车展开了相关研究，蒋旻昱[6]设计了一款带链条的折叠自行车，但是并未对其关键零件进行受力分析；程宪春等[7]提出了设计一款可对半折叠的自行车，但是折叠之后自行车的前、后轮并排分布，体积仍然较为庞大；文献[8]设计了一种自行车折叠车架并利用有限元软件对其进行了受力分析，但是并问对设计变量的敏感性进行分析，影响优化分析速度。

因此，本文提出了设计一款新型的无轮毂折叠自行车，折叠后后轮能套入前轮中，有效的减小了自行车的体积，使其方便搬运与携带。本设计已获国家授权专利 “一种可折叠电动自行车（ZL201621162254.4）”，表明本设计具有一定的创新性。本文主要以质量最轻、高固有频率、位移量小和等效应力低为优化目标函数对自行车车身进行可靠性的轻量化分析，基于灵敏度分析理论，提出了静力学和模态分析的多学科优化时设计变量选择的模糊综合评价方法，有效减少了设计变量数量，提高轻量化优化速度。

1 新型折叠自行车机械结构设计

针对传统的自行车结构简单、体积庞大以及重量大的特点，而设计一款新型轻便的可折叠自行车。本文设计的可折叠自行车，具有无轮毂等特点，能折叠成与一个小汽车车轮大小的体积、质量轻便、可单手提起、方便携带，整车折叠前、后模型图，如图1所示。

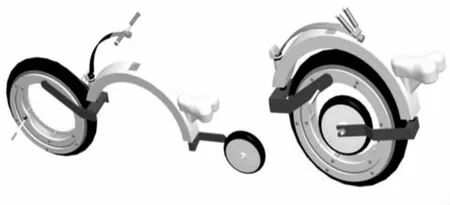
图1 折叠前后的整车模型

1.1 无轮毂前轮设计

前车轮装配图如图2所示，包括环形钢圈以及环形钢圈两侧的环形板，环形板的周部间隔设置有依次穿过环形圈板、环形侧板和环形钢圈，使环形圈板与环形侧板及环形钢圈形成可拆连接的连接螺栓，并且环形侧板与环形钢圈的外圈配合形成与橡胶轮胎的内圈凸部相连接的环形凹槽，与前支撑架上的8个轴承配合。

图2 无轮毂前轮

为了减小自行车折叠后的体积，使得折叠后后轮能恰好放入前车轮中间的位置，将前车轮的外径设计为小于弧形车架的直径，使得折叠后前车轮能置于弧形车架之下，大大减小了自行车的体积。环形侧板的内圈还设置有通过脚踏驱动无轮毂前车轮转动的棘轮机构，方便骑行。

1.2 前轮与后轮支撑架设计

由于本文设计的折叠自行车没有传动链条，因此前支撑架两侧各有4个轴承与前车轮两侧的内外凹槽圈配合，实现前车轮的滚动与支撑作用，如图3所示。为了折叠之后后轮能刚好放入前轮的中间空位，后轮的直径小于前轮的内径，并且后支撑架设计成拐状，如图3所示。

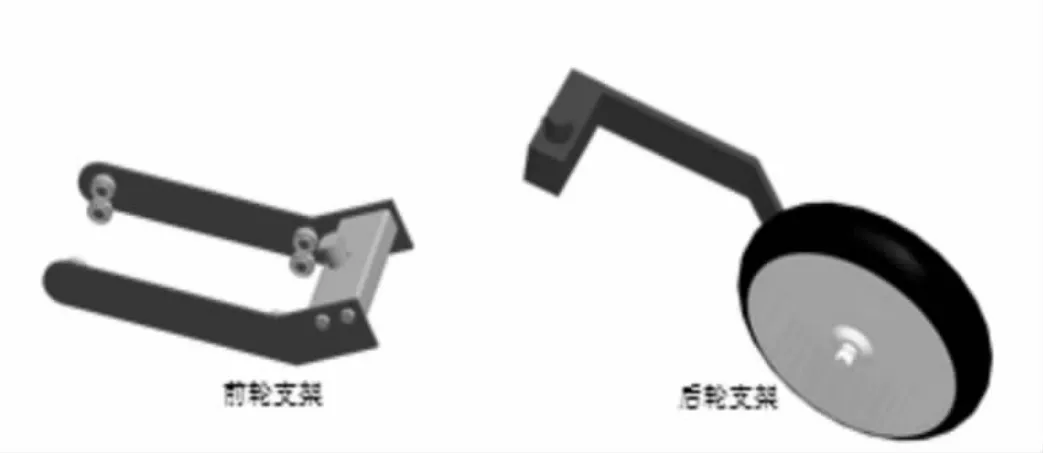
图3 前轮与后轮支撑架

2 多学科响应的分析

2.1 静力学灵敏度分析

根据静力平衡方程有：

式中 [K]、{Y}和{F}分别为刚度矩阵、位移和载荷向量。通常在静力学分析时，载荷向量为恒定值，将式(1)等号两边同时对设计变量求偏导数xn，即有：

式中[Kn]与{Yn}分别为刚度矩阵[K]和位移向量{Y}对xn设计变量所求得的偏导数，且刚度矩阵和位移向量能利用有限元软件分析得到，因此通过式（2）能求得设计变量对其一阶位移的灵敏度，同理可求得应力灵敏度函数。

2.2 模态特征灵敏度分析

根据模态特征方程有：

式中λi、[M]和{ui}分别为结构的特征值、质量矩阵以及节点的位移。将式（3）等号两边同时对xn设计变量求偏导数，然后等号两边同时左乘又因为即特征灵敏度可以表示为：

式中 λi，n、[Mi，n]和{ui，n}分别为特征值 λi、质量矩阵[M]以及节点的位移{ui}对 xn设计变量所求得的偏导数。

通过设计变量的增量Δ{x}可得到质量矩阵与刚度矩阵相应的增量，即Δ[M]和Δ[K]，即可得：

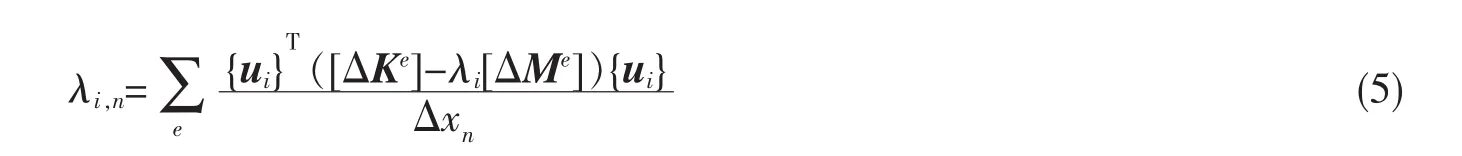
式中Δ[Me]和Δ[Ke]为Δ[M]和Δ[K]在有限元分析中相对应的单元质量矩阵与单元刚度矩阵。

2.3 多学科响应的综合分析

多学科优化设计综合了各个子学科对目标响应的影响，可以采用模糊综合评判法对其进行分析[9-10]。模糊综合评判法是一种在考察被评判事物的隶属等级时，综合了各个因素对其影响的评判方法。

2.3.1 因素集

在模糊综合评判中，建立因素集与评判集的模糊关系矩阵是至关重要的。通常，综合评判向量由所有的设计变量组成，因此因素集U与评判集V的模糊关系矩阵可以表示为：

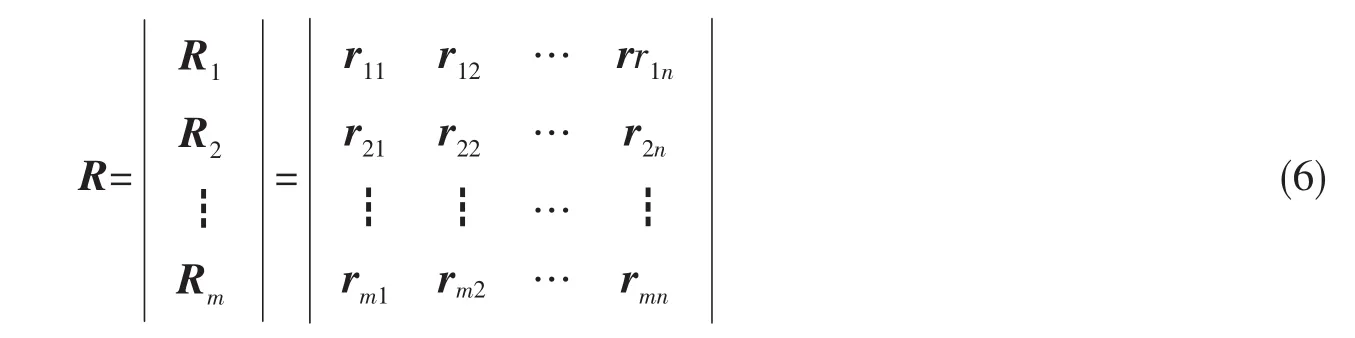
式中m和n分别表示设计变量与目标函数的个数；rmn为对应的灵敏度。

2.3.2 权重分配

权重是用来评价各个因素重要性的量值，权重的确定是否合理对评判结果的准确性具有直接的影响。目前，通常采用专家估测法和主分量分析等方法来确定权重值，各种方法都有各自的优缺点，本文利用专家估测法来确定权重值[16]。

2.3.3 评判集设定

评判集V是表示评判对象所有结果的集合，通过设计人员选取截断水平来确定。当灵敏度rmn大于截断水平时，表示相对应的设计变量对目标函数具有较大的影响，反之对目标函数没有影响。因此，在优化分析时可以通过评判集来减少设计变量的个数，从而提高优化效率。

3 满足可靠性的轻量化设计

为了使设计的新型自行车能方便搬运，要求其应在满足可靠性的前提下质量最轻，因此需要对各个关键零部件进行轻量化的优化设计。由于自行车在行驶过程中因路面不平导致使用者颠簸，所以前、后轮支架所承受的载荷会发生变化。选取后轮支架为研究对象，对其进行可靠性的轻量化设计[11]。

3.1 多学科灵敏度分析

图4 各个参数分布

充分考虑后轮支架各个结构参数对目标函数的影响，对其进行灵敏度分析[12-13]，各个参数的分布情况如图4所示。

3.1.1 静力学灵敏度分析

图5为后轮支架机构最大应力δmax、位移d与等效应力δv对各个参数的灵敏度分析，因为3个响应的敏度值数量级不一致，所以需要其进行归一化处理，以便后续操作。

3.1.2 固有频率灵敏度分析

模态分析时的固有频率能反应出结构的动刚度，图6为支架机构的前四阶固有频率对8个设计变量的灵敏度分析情况，同理对其进行了归一化处理。

3.2 选取优化设计变量

通过模糊综合评价方法选取优化设计变量，不仅可以减少灵敏度小的设计变量，而且能使优化以更快的速度朝着最优解前进。

图5 静力学灵敏度分析

图6 固有频率灵敏度分析

3.2.1 建立模糊关系矩阵

通过以上所求得的各学科灵敏度，利用式(6)建立以下模糊关系矩阵：

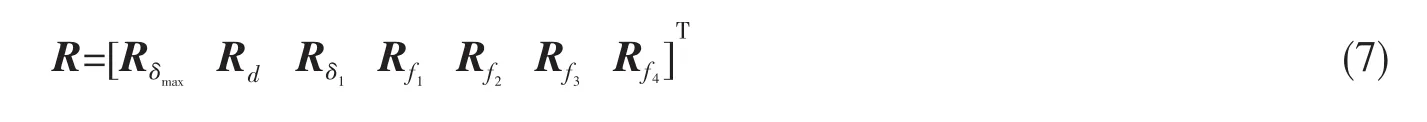
3.2.2 权重的确定

采用专家估测法来确定权重，首先请各个学科的知名专家对静力学结构分析中的最大应力δmax、位移d与等效应力δv与模态分析中的f1,f2,f3，f4确定的权重分别为：

在整个系统的优化分析时，综合静力学与模态分析的影响，确定其权重系数为：

则整个系统的权重为：

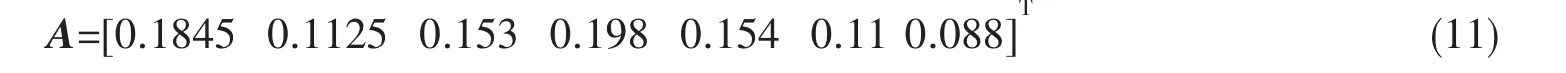
3.2.3 综合评判选取设计变量

因此模糊综合评价为：

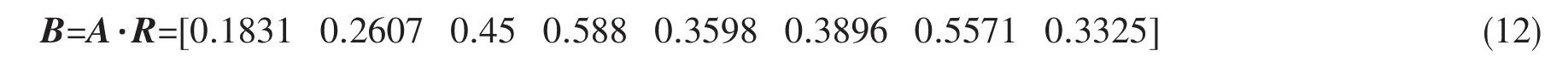
如果截断水平设定为0.2，则选取x2，x3，x4，x5，x6，x7，x8为设计变量进行多学科优化分析；如果截断水平设定为0.3则选取x3，x4，x5，x6，x7，x8为设计变量进行多学科优化分析。本文的截断水平设定为0.3，设计变量的范围如表1所示。虽然只减少了两个设计变量，但是在有限元优化分析时，实验设计组数由81减少为45，优化速度提高了将近1倍，如果设计变量更多的话，优化速度将会有更加明显的提高。

表1 设计变量

3.3 多目标轻量化优化设计

以满载情况下的载荷F、材料的性能为约束条件，以动刚度f2、最大位移量d、最大等效应力δv和质量m为目标函数，以x3，x4，x5，x6，x7，x8为设计变量进行多目标优化设计，即多目标优化问题可以表示为：

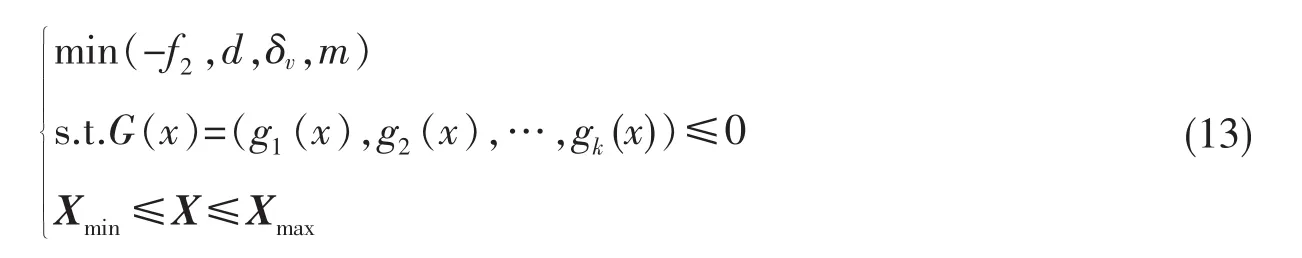
利用workbench建立后轮支架的有限元模型，为提高计算效率，对一些与运输无关的倒角等进行了简化，其中总的单元数目为4598，节点为8661,材料参数为：弹性模量71.7 GPa,泊松比0.33，密度2810 kg/m3，抗压强度455 MPa。在后支架U型槽的3个面施加全约束，在圆柱顶面施加载荷，对其进行轻量化分析优化分析。选取一组优化结果与优化前进行对比，如表2所示。同时图7～8给出了优化前后的位移云图和等效应力云图对比情况。

分析表2可得，优化后支架的质量比原来减少了41.6%，虽然二阶固有频率有所降低、等效应力与最大位移都有相应的提高，但是都在其安全范围以内，安全系数也为2.241，表明经过优化之后可有效的减少后轮支架的重量且能保证其安全的工作。同理，可以对前轮支架与弧形车架等关键受力零部件进行轻量化分析，使整车的质量得到下降。

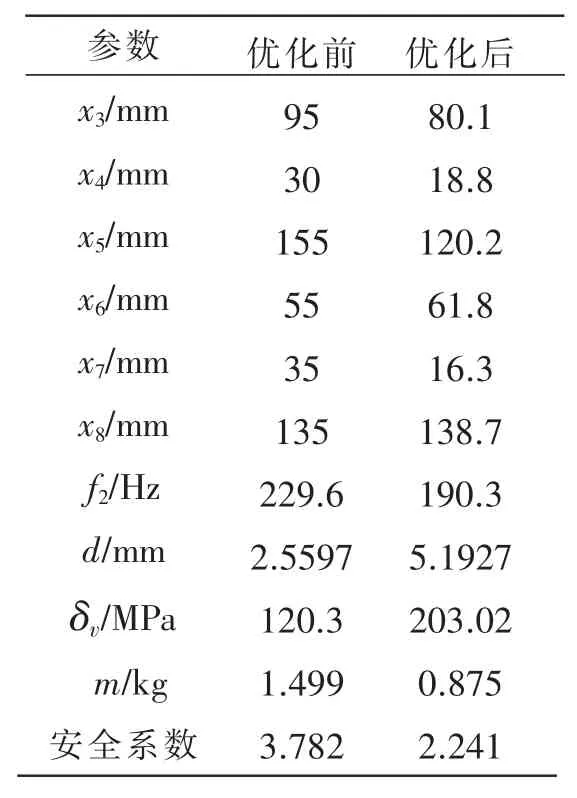
表2 优化前后结果对比

图7 优化前后位移

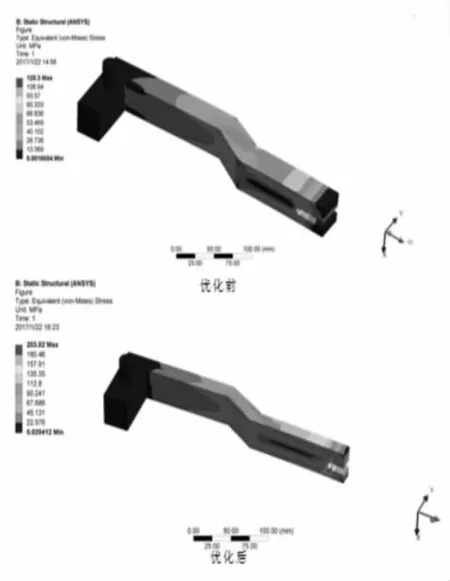
图8 优化前后等效应力

4 结论

基于折叠自行车是当前研究热点，设计了一款新型的无轮毂折叠自行车。建立了静力学和模态分析的多学科优化时设计变量选择的模糊综合评价方法，减少优化的设计变量，提高优化效率。建立自行车关键零件参数化的有限元模型，利用Workbench软件对其进行多目标轻量化优化设计，结果表明所提出的方法能快速、有效的进行满足可靠性的轻量化设计。