MURC 视域下圆形面积求解方法的教学程序设计陆有海

陆有海

一、激活方形面积问题的求解经验，引出圆形面积的求解问题

1．什么是面积？

物体表面或几何图形的大小。

2．长方形面积问题是怎样求解的？

面积问题求解的基本途径就是用面积单位进行直接测量。但是，在实际测量过程中，会遇到不可直接测量的情况，从而，促使人们去探索直接测量面积以外的可行方法。除了直接测量面积以外，人们发现了长方形长与宽的乘积与面积的关系，因此，人们通过测量长方形的长与宽来求解长方形的面积问题。如，长方形的水塘就必须通过测量水塘的长与宽来求水塘的面积。

（1）用面积单位直接测量长方形的面积（测量）。

（2）通过测量长与宽间接测量长方形的面积（测量+计算）。

3．其他方形面积问题是怎样求的？

在长方形面积求解基础上，其他图形面积问题的求解途径，除了直接测量和直接探索解决以外，还可以借助事物之间的关系来求解。

（1）第一种求解思路：（直接测量）直接用面积单位进行测量。显然，长方形面积的直接测量，只要面积单位适当，测量比较方便。但是，其他图形并没有长方形这种方方正正的规范性，因此，直接测量会或多或少遇到“不完整”的问题。

（2）第二种求解思路：（局部割补）局部割补化解直接测量问题，完成直接测量任务。尽管直接测量不能直接解决其他图形的面积测量问题，但是在问题求解过程中，这是必需的过程。只有经历这个过程，才能自然地发现解决问题的办法（局部割补）。显然，这种局部割补方法具有多样性，在问题的求解过程中，我们还必须充分展示这种“充分性”。

（3）第三种求解思路：（整体割补）整体割补是局部割补的一种特殊割补方法，为其他图形面积问题的转化提供重要的手段。整体割补方法的出现基于充分的局部割补，但是它为超越局部割补创新方法奠定了基础。局部割补解决直接测量的问题，整体割补提高了直接测量问题解决的效率，并且，直接将图形转化成了已知求解问题方法的图形。显然，不同的图形，整体割补法具有多样性与差异性。

（4）第四种求解思路：（割补化归）整体割补的成功（事实上）就是问题化归的成功。这种成功为化归前后进行观察比较提供了材料与对象，为发现图形面积的本质问题奠定了基础。

如，平行四边形面积与平行四边形的底与高的乘积相联系；三角形面积与三角形的底与高的乘积的一半相联系；梯形面积与梯形的上底、下底、高之间存在直接的联系。

从视觉上看，面积大小与物体表面（图形）的大小有关。从本质上看，面积大小与物体表面的特征量数及相互之间的联系直接相关。因此，图形（方形）面积由其自身图形的特征量数及其相互关系所决定。因此，在探索未知图形面积问题时，我们需要探寻与面积相关的特征量数，以及它们与面积之间的关系。这是面积问题教学的核心与目标，也是方形面积教学活动需要积累的基本活动经验。圆形面积问题求解的教学活动就是在这种数学经验的引领下起步的。

（5）第五种求解思路：（直接计算）直接计算公式来自于图形的割补化归与推导。直接计算的公式包括：这些图形面积的计算，必须基于图形自身特征量数。

二、探寻图形面积问题的求解方法

1．数学实验途径。

实验是指实际验证图形（面积）自身具有的各种特征量数之间关系的存在性的操作、观察、猜测、发现等数学活动。

圆形面积的数学实验，首先要理清相关的特征量数（圆的周长、圆的半径、圆的直径），事实上，决定圆的面积大小的特征量数就是圆的半径。因为，在圆的认识中，已经知道圆的半径决定圆的大小（半径决定了直径，半径决定了周长）。也就是说，影响圆形面积的关键因素事实上就只有一个，那就是圆形的半径。因此，我们只需研究圆形面积与圆形半径之间的关系。

表1：半径分别为1、2、3、4的圆的面积的实验数据（测量结果）

?

研究圆的面积的实验，我们总是选取可以测量面积与半径的圆形进行研究，而圆形的面积用直接测量来获得准确的数值似乎是不可能的，因此，关于圆形面积与圆形半径的关系的实验似乎存在着较大的困难。事实上，我们也只能发现一个近似的关系。尽管发现的是近似关系，但是也不能否定这种实验的数学价值。

通过实验我们借助估计分别获得了不同半径下的圆形面积的估计值，如表1所示，估计结果与半径的关系，在教师的引导下，可以发现一个大致的关系：S圆形≈3r2。

圆形的特征决定了我们的实验不可能获得完全准确的圆形面积与圆形半径之间的关系。

类似于圆的周长的实验方法来解决圆的面积问题，当然，也可以用更小的单位（方格）来计量，会使估计值更逼近精确值，但是，这种实验结果的误差还是不能忽略。

2．问题化归途径。

将圆形面积的求解当作一个问题，解决问题的总体策略，或为直接求解（实验法就是一种直接求解的方法），或为化归求解（将未知问题转化为可求解的问题）。

化归策略求解圆形面积问题，需要理清两件事：一是求解的问题是什么？二是求解问题可以化归的对象问题是什么？

在圆面积求解问题中，求解的问题：一个直径（半径）为d的圆形面积是多少？求解问题可以化归的对象问题：已知长与宽的长方形面积、已知边长的正方形面积、已知底与高的平行四边形面积或三角形面积、已知上底与下底及高的梯形面积。

因此，问题化归求一个已知直径或半径的圆形面积问题，重要的事情在于：确定化归的基本对象与探寻化归的有效方法。

怎样才能确定化归的基本对象？怎样才能探寻化归的有效方法？思路与逻辑主要还是产生于方形面积的求解经验。

方形面积求解经验主要有：用最基本的测量方法直接度量；局部割补再进行直接度量；将图形割补化归。因此，圆形面积问题的求解将在这些经验的基础上来展开。

图1：度量圆形面积

（1）到定义，尝试度量求解——积聚探索动力。

面积是指平面图形的大小，即含有多少个面积单位。根据图形的实际情况，我们可以选定适当大小的面积单位来测量平面图形的面积。圆形不是方形，无法直接度量面积，如图1所示，要进行割补也具有一定的困难。当然，我们也可以尝试取更小的面积单位，但是，面积单位太小，操作就显得十分繁琐。因此，我们已经不太可能通过割补获得准确的圆形面积。但是，在这个直接度量的过程中，我们可以发现，如图1（右）所示，圆形面积与圆形的外切正方形面积之间的大致关系：圆形面积大约是圆形外接正方形面积的四分之三，即显然，3r2＜S圆＜4r2。

根据圆形直径与圆形周长之间的关系的探索经验，我们也曾经获得到一个类似的关系，即3d＜l＜4d，最后，根据实验结果，我们有l圆=dπ。因此，我们也必然会获得一个有趣的猜测性结果：S圆=r2π。

（2）向科学，尝试实验求解——体验无奈现实。

有了完美的猜想，需要有客观实践的支持。在科学研究中，“实验”是一种科学的研究方法。但是，实验就是要真实地通过测量获得相关数据，来发现与验证相关的猜测。因此，我们会进一步去审视圆形面积与半径之间的关系：S圆÷r2=？，进一步去探寻圆形面积的有效测量方法。但是，鉴于曲直之间难以通过有效割补的方法来实现转换，我们已经处于山前无路的窘境了。

（3）主回家，尝试方法创新——体验奇妙数学。

“窘境”在于用较大的面积单位测量精确度不高，“窘境”也在于用较小的面积单位测量数量太多，“窘境”还在于较大与较小面积单位混合测量的结果没有什么规律，而且大小不等的面积单位还不可以直接相加！也是说，“窘境”窘在无法逼近，无法叠加！

图2：可逼近可叠加的面积分割方法

在圆形中，我们尝试着进行不同的分割。显然，将其分割成平行四边形与梯形不太可能（圆形是轴对称图形，平行四边形不是轴对称图形）；将其分割成长方形与正方形也不能分割成若干个相同的长方形与正方形。不过，让我们意想不到的惊喜却是三角形，我们往往没有想到，圆形可以分割成若干个相同的等腰三角形；当分割的份数不断地增多时，若干个三角形的面积之和可以不断地接近圆形面积。这样，完全满足可以逼近，还可以叠加求和的要求。这样，等腰三角形就成为一种测量圆形面积的“专用”单位。

设三角形△B1B2O 的高为 hi，底为 ai，则

设将圆形平均分割成n份，则可以构造出n个等腰三角形，则n个等腰三角形面积的和为

显然，当圆形分割的份数不断增多时，三角形底边长与其对应的圆弧长就会不断地接近，三角形的高就越来越接近圆形半径的长度。

因此，我们假设把圆形平均分割成无限多个近似的三角形，这时，所有等腰三角形底边之和正好就是圆形的周长（nai=l），等腰三角形底上的高正好就是圆形的半径（hi=r）。因此，圆形面积就是这些三角形面积的和，

（4）助经验，化归解决问题——感知多样方法。

图形面积化归的基本思路，主要有三种情况：一是多个图形拼成一个可以求解的图形；二是将一个图形分割成多个可以求解的图形；三是将一个图形割补（分割拼接）成一个可以求解的图形。显然，多个圆形是无法拼成一个可以求解的图形的；一个图形分割成多个可以求解的图形，而且是多个相同的小三角形，这是一种很奇妙的思路；如图3（左）所示，将圆形分割成8个相同的小三角形（小扇形），那么，理论上，它可以拼成长方形、三角形、平行四边形、梯形等多种图形。

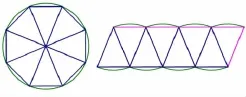
图3：圆形割拼成（类似）平行四边形

如图3所示，圆形割拼成了类似平行四边形，当分割的份数不断地增多时，三角形底边长与对应的圆弧长就不断接近。因此，圆形面积求解问题可以转化为平行四边形面积的求解问题。

因此，我们可以知道：圆的面积与半径的大小直接相关，测量圆形面积的问题可以通过测量圆形半径来解决。

三、重复训练巩固数学知识，概括总结积累活动经验

关于圆形面积的数学学习，就数学知识而言，圆形面积公式是一个重要的基础知识；根据相应的条件求解面积公式中的相关的特征值是一个重要的基本技能；探索圆形面积公式所需的分割拼补、想象推理等化归思想与推理思想是重要的数学思想；在圆形面积求解过程中，运用测量、分割、拼摆、想象等数学方法求圆形面积问题，这种回家式思维、化归式思想、无限式想象是重要的数学活动经验。

1．形式化训练。

说一说面积的计算公式：S圆=r2π，其中，S表示圆的面积，r表示圆的半径。

用一用面积的计算公式：已知圆的直径或半径或周长，求圆的面积。

2．实践性训练。

（1）测量给定图形的直径（或半径）长度，计算圆形的面积。

（2）测量给定圆形事物（柱子等）的周长，计算圆形的面积。

（3）解决日常生活中圆形建筑与圆形装饰的用料面积。

3．发展性训练。

说一说圆形面积计算公式是怎样的（数学知识）？说一说圆形面积计算公式是如何获得的（数学过程）？说一说获得圆形面积计算公式的体会是什么（数学体验、数学经验）？关于圆及圆的面积你还知道了什么（数学文化层面的拓展）？