Effect of hydrophobicity on the water flow in carbon nanotube—A molecular dynamics study

Hamed Esmaeilzadeh, Junwei Su, Majid Charmchi, Hongwei Sun*

Department of Mechanical Engineering, University of Massachusetts Lowell, Lowell, MA 01854, USA

Keywords:Molecular dynamics Contact angle Interaction-energy-coefficient Water flow Carbon nanotube

ABSTRACT This work focuses on the study of the effect of hydrophobicity on the water flow in carbon nanotubes (CNTs) using a molecular dynamics (MD) approach for a wide range of potential applications such as water purification and high efficiency of nanofluid energy absorption systems(NEAS). The hydrophobicity between liquid water and surface of CNTs was characterized by interaction-energy-coefficient (IEC)—a parameter describing the energy interaction strength between water molecules and carbon atoms. It is shown that the static contact angles between water and carbon surface decrease from 155° to 44° when the values of IEC increase from 0.042 kJ/mol to 2.196 kJ/mol. In addition, the pressure drops in CNT became independent of IEC when the IEC value was higher than 1.192 kJ/mol for a given flow rate. It was found that the hydrophobicity of CNT surface has a significant impact on the pressure drop of water flow in the CNTs and MD method provides a quantitative evaluation of the impact.

Carbon nanotube (CNT) is one of the most promising nanomaterials due to its high thermal and electrical conductivities and low thermal expansion coefficient that make them well suitable candidates for various applications such as water purification [1], biomolecular sensors [2], drug delivery systems [3], hydrogen storage medium in fuel cells [4], carbon nanopipettes [5],and high efficiency of nanofluid energy absorption systems(NEAS) [6]. For example, CNT membrane has been studied as the filter materials for water purification or desalination system[7]. Also, some researchers proposed to use CNT membrane as nanosyringes to deliver drugs in which the drug is released through cellular membrane [8]. Therefore, it is very critical to understand the water flow behavior in CNTs for a better design of nanofluidic-based systems for the stated applications.

As the effect of surface forces in the nanoscale becomes significant, the continuum assumption breaks down and the water flow in nanoscale channels exhibits significantly different behavior from the flow in the macroscale and/or microscale channels [9]. The hypothesis of nonslip boundary condition, applied in large-scale analyses, may not be valid in nanoscale systems[10, 11]. As a result, the slip velocity at the wall could lead to higher flux of flow in comparison to nonslip continuum condition [12-15].

Considering the experimental study in nanoscales is still a great challenge, theoretical and numerical models are widely used for understanding the behaviors of fluid flow in CNTs under various situations [16-19]. As an experimental computation method in simulating kinetic behavior of substance at molecular and atomic scales, molecular dynamics (MD) has been widely utilized to simulate fluid behaviors at nanoscale channels, enabling prediction of behavior of fluid flows and observation of the fluid/wall interface effects [20-22]. Briefly, MD is a deterministic simulation method, in which the atomic trajectories of fluid particles are tracked by numerically solving Newton's equation of motion based on a specific interatomic potential and certain initial and boundary conditions [23, 24]. For the simulation of water molecules in CNT, the pairwise interaction between water molecules and carbon atoms (Uwc), was generally modeled by the so-called Lennard–Jones (LJ) potential energy [25].

Hummer et al. [26] employed two different values for the interaction parameters between water molecules and carbon atoms in their MD simulation. The results showed that small changes in these parameters caused different occupancy of water molecules in CNT—two state transitions between empty and filled states. Thomas and McGaughey investigated the pressure driven water flows through CNTs with diameters ranging from 1.66 nm to 4.99 nm using MD simulation. Their results revealed that the ratio of the observed flow rate from MD simulation to that predicted from the nonslip Hagen–Poiseuille relation decreased with increasing CNT diameter and varied from 433 to 47[27]. Joly [28] studied the effect of liquid/wall slip on dynamic of capillary tube filling in nanometric pores where it was found that for water flow in CNT, there was no shear stresses inside the liquid. Therefore, viscous term is only based on the friction coefficient of liquid at the wall and the liquid viscosity does not play a role. Nichollas et al. [29] employed the non-equilibrium molecular dynamic (NEMD) method to study the water flow in CNT to examine the length effect on the internal flow dynamics. Their results showed that under similar applied pressure difference,an increase in CNT length had no effect on the mass flow rate and fluid flow velocity. Liu et al. [30] investigated the pressuredriven water transport inside the nanotube formed by graphene bilayers through molecular dynamics simulation. Their results showed the water flow rate increases linearly as the applied pressure gradient increases. The weak viscous effect and therefore the very low friction at the channel walls is the key factor for achieving fast flow rates in nanotubes. Recently, Ganjiani and Hossein Nezhad [31] used MD simulation to study the effect of carbon/water interaction parameters on NEAS. It was found that the contact angle was reduced by increasing values of the energy and distance parameters of LJ potential. As mentioned earlier, these parameters are related to interaction’s strength and distance between water molecules and carbon atoms, respectively. Cao and Liu [32, 33] studied the working mechanism of energy absorption in NEAS under impact load using MD simulation. Their results confirmed that NEAS can be a promising tool to protect against high speed load rate. All of simulations performed so far employed different values of interaction parameters for MD simulation which heavily rely on the methods which were used to determine these interaction parameters [34].These methods include Moller-plesset perturbation theory of the second order (MP2) [35], random phase approximation (RPA)[36], diffusion Monte Carlo (DMC) [36], density functional theory-symmetry-adapted perturbation theory (DFT-SAPT) [37],density functional theory/coupled cluster (DFT/CC) [38], density functional theory with dispersion correction (DFT-D) [39],and coupled cluster treatment with single and double excitations and perturbative triples (CCSD(T)) [40]. These interactionenergy-coefficients (IECs) values leads to different surface hydrophobicities of CNT from hydrophilic [28] to hydrophobic ones [41, 42]. In addition, a review of the previous works showed that CNT can be modified to form different surface hydrophobicities [43-45] and a different surface property can be achieved for a desired application by selecting specific functional groups coated onto the CNT surface [46-48].

The focus of this research is to explore the hydrodynamic behavior of water flow in a CNT connected between two reservoirs,where water is driven by two moving pistons. First, the relationship between IEC and hydrophobicity of water molecules on carbon atoms was quantified through the change of contact angles of a water drop on carbon surface. Then the effect of the hydrophobicity on the water flow in the nanotubes was investigated in terms of pressure drop, axial density and axial velocity distributions.

The MD model system consists of a CNT, two reservoirs at the two ends of CNT, two moving pistons of graphene, and water molecules confined in CNT and reservoirs, as shown in Fig. 1.

The simple point charge (SPC) model for water molecules was utilized in this research since it reproduces the transport properties of water close to experimental results [49]. The integration of equations of motions were performed using Verlet algorithm in the canonical network virtual terminal (NVT) ensemble by using LAMMPS software [50]. The time step of simulation was set to be 1 fs (1 fs = 1 × 10–15s) and the cut-off radius of LJ potential energy was 8 Å (1 Å = 1 × 10–10m). The energy and distance scales between water molecules and carbon atoms were= 0.389 kJ/mol and= 3.283 Å, respectively [51]. The long range Columbic interaction was computed with Ewald technique to consider the electrostatic charge between water molecules [52]. The boundary conditions were periodic in all of directions.

The CNT has different atomic arrangements including armchair, zigzag, and chiral [53]. The zigzag CNT was used in this study with radius of 5.45 Å and length of 25.3 Å. Based on dimensions of CNT and density of water at 298 K (1 g/cm3), the number of water molecules contained in the zigzag CNT was about 80 [51]. The water reservoirs with the dimensions of 29.82 Å ×27.69 Å × 10.2 Å contains 297 water molecules assuming the density of the water 1 g/cm3. Two pistons are moving downward with constant velocity of 10 m/s. The initial locations of the water molecules and carbon atoms were built using the opensource MOLTEMPLATE software, a general text-based molecule builder [54].

Fig. 1. Schematic of the water flow system in a CNT including water molecules, two moving pistons of graphene and CNT atoms.

To validate the MD model, the simulation result performed in this study by LAMMPS software [55] was compared with the data reported by Liu et al. [51] and the comparison is presented in Fig. 2. The CNT radius of 7.85 Å was used in the simulation. It can be seen that the density profile obtained from MD simulation is in a good agreement with Liu’s result.

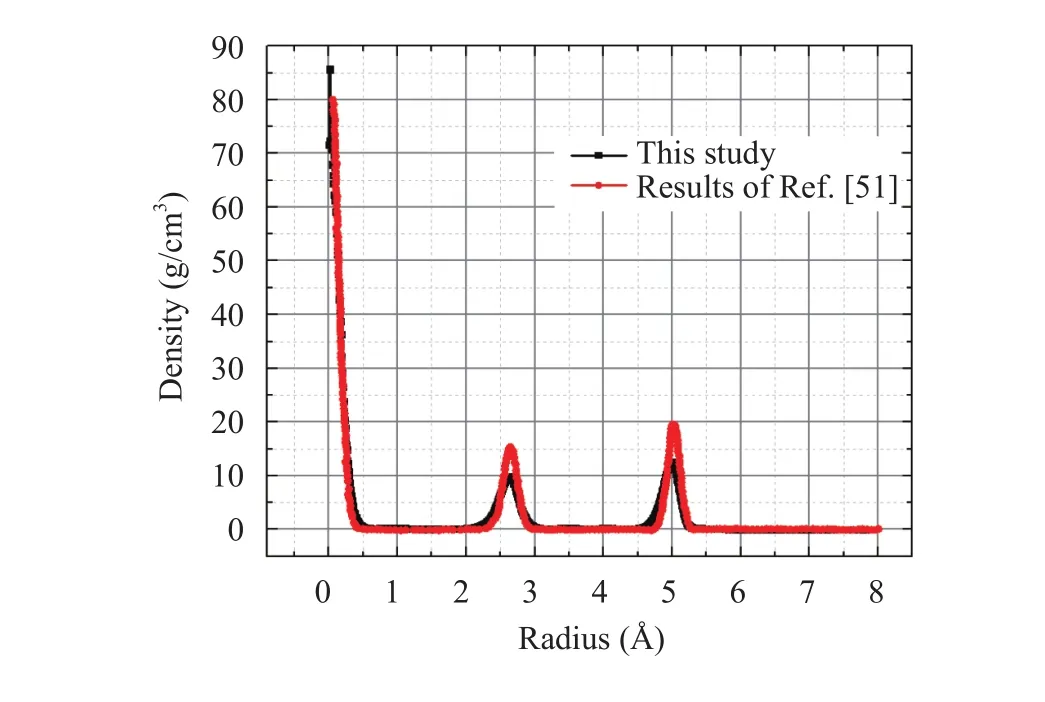
Fig. 2. Comparison of the simulation results of water flow in a CNT(radius = 7.85 Å) without the presense of reservoirs and pistons with the data published by Liu et al. [51] at 298 K and water density of 1 g/cm3.

The MD simulation results shows that there is almost no molecule in the region near the wall of the CNT. The reason is that the carbon atoms and water molecules tend to keep a distance of approximately= 3.283 Å from each other [56]. There are two density peaks appearing at radius ofrof 2.5 Å and 5.0 Å.Wang et al. [57] proposed an equation to calculate the number of layers n that are formed completely in the CNT with radius of Rnas follows:

Based on values of σO-O= 3.166 Å, σC-O= 3.283 Å and radius of Rn= 7.85 Å, two layers of water were formed completely which is consistent with the results shown in Fig. 2. Equation (1) indicates that with increasing the CNT diameter, the number of layers will increase and the ordered structure of water molecules in CNT will be disappearing to the bulk condition. The similar layered structure and solid-like distribution of water molecules in CNT with various diameters was described in our previous work [58]. Alexiadis and Kassinos [56] proposed a correlation between the overall density of water and CNT diameter as follows:

where ρ0is the density of bulk water. The values of ρ*and d*are caluclated by:

As Eq. (2) shows, with increasing CNT diameter, the density of the water molecule is approaching to that of bulk water condition. Our previous results also showed that by increasing the diameter of CNT, the results of density approached to the bulk condition (1 g/cm3) [58] as predicted by Eq. (2).

The effect of various IEC on the hydrophobicity was inspected as the IEC is directly related to the interaction force and energy between water molecules and carbon atoms [25] and the values of IEC were changed from 0.042 kJ/mol to 2.196 kJ/mol[45, 59].

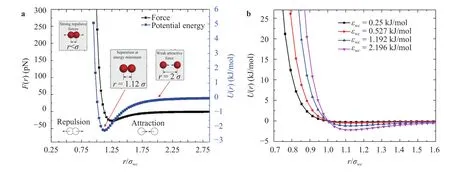
Fig. 3. a Force vs. distance between water molecules and carbon atoms for IEC of 2.196 kJ/mol (1 pN = 1×10-12 N). b Interaction energy vs. distances for different values of IECs.

Figure 3(a) describes the interaction force and energy between water molecules and carbon atoms versus particle distances for IEC at εwc= 2.196 kJ/mol. It can be seen that at equi-librium distancero=the interaction force vanished and the interaction energy reached the minimum value (− εwc). When the distances between particles is less thanro, the particles will repel each other while when the distance is greater than 1.12σ,the interaction force between particles became attractive. Figure 3(b) shows the interaction energy between water molecules and carbon atoms versus different values of εwc. As can be seen, with increasing values of the IEC, the interaction energyUwcincreases and the equilibrium distance, wheredU/dr|r=requilibrium=0 becomes larger.

The effect of IEC on the hydrophobicity was identified by measuring the static contact angle of a water droplet on carbon surface using MD model where the value of IEC was varied from 0.042 kJ/mol to 2.196 kJ/mol [60-63]. For this purpose, 2000 water molecules and a graphene surface consisting of 5408 carbon atoms were employed. The total simulation time was 0.045 ns(1 ns = 1×10–9s) so that a stable contact angle was reached between the water drop and graphene surface. Then, using the curve fitting toolbar in MATLAB software, the droplet contact angle was determined. The change of static contact angle with IEC for a simulation duration of 0.045 ns is presented in Fig. 4.

Fig. 4. The dependence of static contact angles of water droplets on a graphene sheet vs. IECs at t = 0.045 ns.

The MD results show that the contact angle as high as 155°can be reached representing a superhydrophobic state when the value of IEC is low (= 0.042 kJ/mol). With the increasing,the contact angle decreased from 155° down to as low as 40°demonstrating the transition from hydrophobic to hydrophilic states. In addition, after the value of IEC reached about 1.192 kJ/mol, the further increase of IEC values could not reduce the contact angle value any further and the graphene surface displayed a hydrophilic state. Further study is underway to explore this phenomenon.

The water flows in CNTs were simulated using the MD model under different IEC values to quantify the effect of hydrophobicity. Figure 5(a) shows the solid/liquid interaction energy per unit area of the CNT as function of IEC () at the simulation time of 0.04 ns (tsimulation= 0.04 ns). The results show that the interaction energy (Uwc) increases almost linearly with the increasing of the IEC value as predicted by LJ potential energy [25].

Then the water flow in a CNT described in Fig. 1 was simulated under different IEC values and the pressure drops along the CNT are presented in Fig. 5(b). It can be seen that at the low IEC values the pressure drops along the CNT are low due to the weak interactions between the water molecules and carbon surface. As the interaction between water molecules and carbon atoms become stronger, as indicated by larger IEC values, the pressure drops increased sharply due to the increased friction forces caused by strong interactions between water molecules and carbon surface. The pressure drop reached a stable value when the IEC reached 1.192 kJ/mol, where the surface became hydrophilic. The trend of the pressure drop increase is consistent with the decrease of the contact angle presented in Fig. 4.

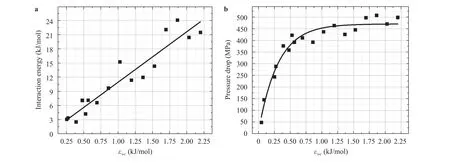
Fig. 5. a Interaction energy between water molecules and CNT atoms. b Pressure drop along CNT vs. IECs at tsimulation = 0.04 ns for the water flow at 298 K and density of 1 g/cm3 in the presense of two reservoirs and two moving pistons with the constant velocity of 10 m/s.

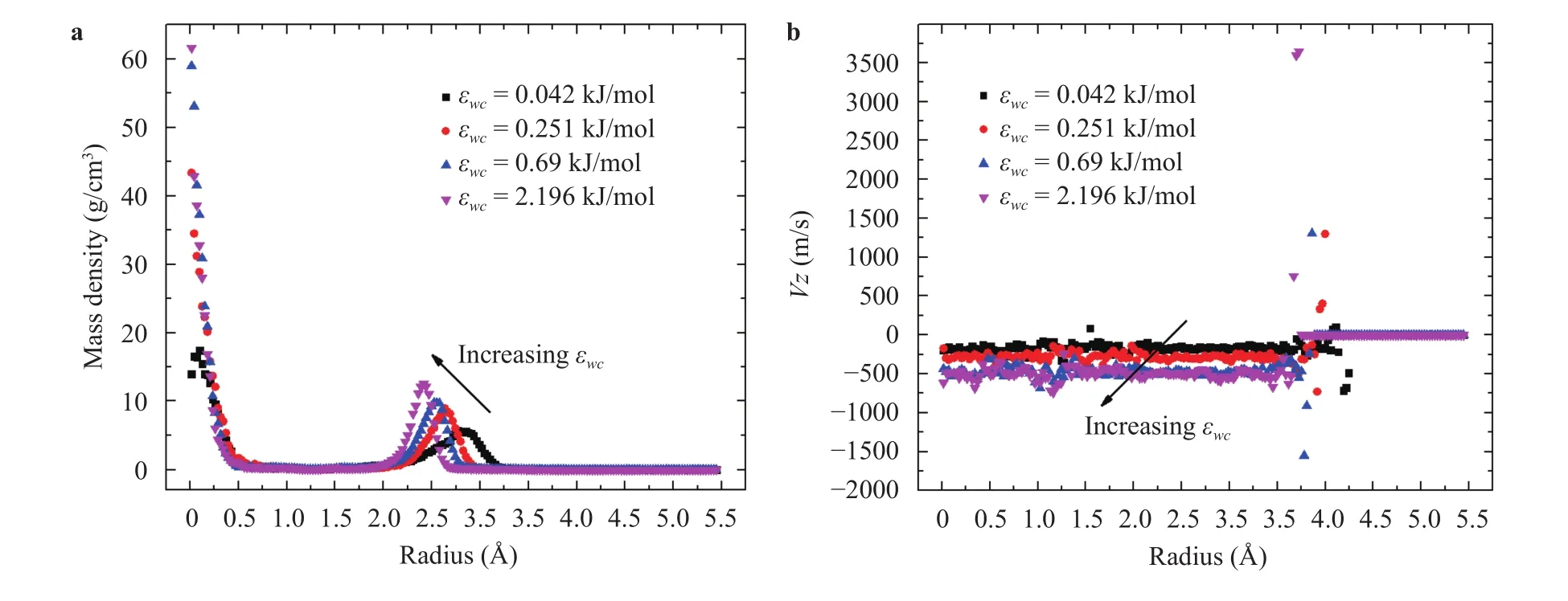
Fig. 6. a Mass density and b velocity distribution in axial direction inside CNT for different values of IECs for the water flow at 298 K and density of 1 g/cm3 in presense of two reservoirs and two moving pistons with constant velocity of 10 m/s.

Figure 6(a) presents the mass density distribution in the axial direction of the water molecules under different IECs. As the IEC increase, the mass density peaks of water molecules tends to move to the centerline of CNT. It is believed that the redistribution of the water molecules in CNT was due to the change of the ordered configuration of the hydrogen bond network between molecules. The hydrogen bonding is an attractive interaction between a hydrogen atom of one water molecule and a negative oxygen atom of another water molecule [64]. As a result, the water molecule can make four hydrogen bonds such that the average number of hydrogen bonds per molecule for the bulk water varies between 2.4 to 3.9 for different water models [65, 66].However, for the water molecules in the CNT, the average number of hydrogen bonds per molecule decreases to 0.9, where only one single chain is allowed to move due to the space limitation[67, 68]. In the meantime, the layered structures of water molecules in a CNT behave as a spring with a resonant frequency of vibration due to the hydrogen bonds. The transport of layered structures in confined systems proceed as a wave motion with Eigen frequencies which can be determined by the CNT size [69,70]. As can be seen in Fig. 6(a), two mass density peaks were formed in the CNT—one at the center of the CNT and the other at the radius of. With the increasing value of IEC from 0.250 kJ/mol to 2.196 kJ/mol, the values of mass densities at the two peaks increased which is consistent with the results reported by Köhler et al. [71]. Furthermore, the location of the second peak moved closer to the CNT center. It is believed this movement is due to the stronger interaction between the carbon wall and the water molecules which is less favored energetically. This is consistent with the results of pressure drop in Fig. 5(b) which realved that for larger values of IECs a higher pressure (energy)was required to push water molecules through the CNT. Therefore, the water molecules preferred to move toward the center with increasing value of IEC. Figure 6(b) presents the results for velocity distribution of water molecules in axial direction through the CNT for different values of IECs. As can be seen there, the water flow in the CNT was similar to a plug-like flow which was reported in Refs. [72-74]. The friction force between water molecules and the CNT atoms resulted in a stepwise variation of velocity profile which was consistent with those results of Hanasaki and Nakatani [72]. With the increasing IEC, the friction force became larger leading to a larger jump in the streaming velocity profile near the wall. In addition, the increasing values of IEC caused the increases of the axial velocity in the CNT.This is because with the increasing value of IEC, higher pressure(energy) was transferred on water molecules as shown in Fig. 5b leading to increases of axial velocity.

In this research, the effect of wall hydrophobicity of CNTs on the hydrodynamic behavior of water flow was studied through MD simulation. The hydrophobicity of CNT was changed by selecting various values of IEC from 0.042 kJ/mol to 2.196 kJ/mol while the contact angle decreased from 155° to 40° indicating the transition from hydrophobic to hydrophilic states. When the values of IEC were higher than 1.192 kJ/mol, the static contact angle didn’t reduce anymore and the graphene surface displays hydrophilic states. The results for pressure drop, axial density and axial velocity of water flow in CNT in presence of two reservoirs were presented. Based on the MD numerical simulation, plug flows were observed in CNTs compared to the parabolic profile for a water flow under continuum flow condition. More importantly, the results showed that with the increasing of IEC and stronger interactions between water molecules and wall carbon atoms, pressure drops quickly increased due to the increased friction forces. However, when the IEC reached 1.192 kJ/mol, the CNT surface became hydrophilic and the pressure drop reached to a maximum and stable value. The results were consistent with the minimum contact angle obtained by the MD simulation for a water drop on the graphene surface.