Principal and internal resonance of rectangular conductive thin plate in transverse magnetic field

Jing Li, Yuda Hu*

a Key Laboratory of Mechanical Reliability for Heavy Equipment and Large Structures of Hebei Province, Qinhuangdao 066000, China

b School of Civil Engineering and Mechanics, Yanshan University, Qinhuangdao 066000, China

c Department of Basic Teaching Tangshan University, Tangshan 063000, China

Keywords:Magneto elastic Conductive thin plate Principle-internal resonance Multiple scales Galerkin method

ABSTRACT The principle and 1:3 internal resonance of a rectangular thin plate in a transverse magnetic field is investigated. Based on the magneto-elastic vibration equation and electromagnetic force expressions of the thin plates, the nonlinear magneto-elastic vibration differential equations of rectangular plates under external excitation in a transverse magnetic field are derived. For a rectangular plate with one side fixed and three other sides simply supported, the two-degree-offreedom nonlinear Duffing vibration differen-tial equations are proposed by the method of Galerkin. The method of multiple scales is adopted to solve the model equations and obtain four first-order ordinary differential equations governing modulation of the amplitudes and phase angles involved via the first-order or the second-order primary-internal reso-nances. With a numerical example, the amplitude frequency response curves, time history responses, phase portraits and Poincare maps of the first two order vibration modes via principle-internal resonance are respectively captured. And the effects of external excitation amplitudes, magnetic field intensities and thicknesses on the vibration of system are discussed. The results show that the response is dominated by the low mode when principle-internal resonance occurs. The internal resonance provides a mechanism for transferring energy from a high mode to a low mode.

The rectangular thin plate structures are widely used in aerospace, space station and other fields. It has important theoretical and engineering significance in the research on complex mechanical behaviors of conductors under electromagnetic field and mechanical field. Many researchers have done many studies on the theory and application of electro-magneto-elastic mechanics. Moon and Pao [1] investigated theoretically and experimentally the regions of instability of cantilever beam plate in a transverse magnetic field. A set of basic equations for free vibration of ferromagnetic conducting plates in a transverse magnetic field were presented, in which the coupled effects of magnetization and eddy current on the mechanical behavior of the plate were included in Ref. [2]. Zhu et al. [3] studied the multifield coupling mechanical behavior of the simply-supported conductive rectangular thin plate under the condition of an ex-ternally lateral strong impulsive magnetic field. A stability analysis was conducted for sub-harmonic resonance and simultaneous resonance conditions of a magneto-elastic translating beam having prismatic joint for higher resonance conditions is studied in Ref. [4]. Based on Kirchhoff hypothesis the problem of vibrations of conductive plate in a longitudinal magnetic field was brought to the solution of the singular integral-differential equation with ordinary boundary conditions. Baghdasaryan et al. [5] solved the formulated boundary-value problem and investigated the influence of magnetic field on the characteristics of vibration process of the examined magneto-elastic system.The parametric instability regions of a cantilever beam with tip mass subjected to time-varying magnetic field and axial force was studied and the influence of magnetic field, axial load,damping constant and mass ratio on the parametric instability regions were investigated by Pratiher and Dwivedy [6]. The nonlinear magneto elastic vibration equations of a conductive thin plate in transverse magnetic field [7] were given and the complex dynamics of the system under sub harmonic resonance [8]and strongly nonlinear sub-harmonic resonance [9] were analyzed. Considering geometric nonlinearity and thermal effect,Hu and Zhang [10] investigated the magneto-thermo-elastic coupled dynamics modeling for axially moving carry current plate in magnetic field. The nonlinear force-electro-magnetothermo-elastic coupled vibration equations were deduced for the first time by using Hamilton principle.

With the development of modern nonlinear dynamic theory and the continuous improvement of numerical methods and techniques for nonlinear vibrations, many scholars have studied the nonlinear vibration problem of the system with new analytical methods [11].

Internal resonance is one of the unique phenomena in nonlinear vibration which are distinct from linear vibration. For multiple-degrees-of-freedom (MDOF) system, when the parameters of the system change to make some natural frequencies of the system commensurable or nearly commensurable, there will have mutual interference between different modals which lead to energy exchange between the interferential modes. The internal resonance can exist independently in free vibration system, and can also occur simultaneously with external resonances which excited by external excitation. Many researchers have investigated the dynamics of the system under internal resonance. Vitt and Gorelik [12] were among the first to show theoretically and experimentally the two-to-one internal resonance with the energy exchange from one subsystem to another using the simplest two-degree-of- freedom mechanical system as an example, research interest to the problem of the internal resonance in mechanical systems has always been strong. The nonlinear response of rectangular and square metallic plates subject to transverse harmonic excitations was studied, also the stability of steady-state solutions and Bifurcation points and their types were investigated in Ref. [13]. The vibrations with three-to-one internal resonance of multiple stepped beams with cubic nonlinearities were analyzed under different boundary conditions by Tekin et al. [14]. Stability and bifurcation behaviors for a model of simply supported functionally graded materials rectangular plate subjected to the transversal and in-plane excitations are studied by means of combination of analytical and numerical methods under the case of 1:1 internal resonances and primary parametric resonance [15]. A two-degree-of-freedom nonlinear nonautonomous system governing equations of motion for the rectangular thin plate with 1:1 internal resonance was derived by the von Karman type equation and the method of Galerkin and restrictions on the damping, excitation, and detuning parameters are obtained, under which the multi-pulse chaotic dynamics was also expected [16]. The method of multiple scales was utilized to investigate nonlinear vibration of a composite laminated cantilever rectangular plate under 1:1 internal resonance [17] or a buckling beam under 1:1 and 1:3 internal resonance conditions [18]. Nonlinear dynamics of a viscoelastic buckled beam subjected to primary resonance in the presence of 2:1 internal resonance was investigated for the first time. And the influence of external excitation amplitude and viscoelastic damping on vibration was discussed [19]. In the presence of 2:1 internal resonance Chen et al. [20] investigated the forced vibration for two elastically connected cantilevers, under harmonic base excitation. Sahoo et al. [21, 22] analyzed the dynamic response of an axially accelerating viscoelastic beam subject to two-frequency parametric excitation under the condition of combined resonance, primary parametric resonance and internal resonance.From the review of literature, it is found that there are many studies only about the magneto elastic vibration or only on internal resonance of the beam, plate and shell, but the investigation of the conductive plate in the magnetic field via forced excitation and internal resonance has not been explored yet.

The objective of this study is to investigate the nonlinear dynamics characteristics of a rectangular conductive thin plate via primary resonance and internal resonance under the suitable boundary condition. The nonlinear magneto elastic vibration equation is derived for rectangular thin conductive plate with one side fixed and three other sides simply supported in a constant magnetic field. Four non-linear ordinary-differential equations governing modulation of the amplitudes and phase angles of the interacting modes under 1:3 internal resonance conditions are obtained by the method of multiple scales. And we also analyze the effects of parameters such as magnetic field, excitation amplitude on primary and internal resonance.

Considering the thin rectangular conductive plate in an external transverse magnetic field0(0,0,B0z), we establish the Cartesian coordinate systemOxyzin magnetic field (is the middle plane of the plate andzis along the normal direction of the middle plane as shown in Fig. 1.

Based on Kirchhoff’s fundamental assumption and accounting for the coupling effect of mechanical field and electromagnetic field, we can obtain the nonlinear magneto-elastic vibration equation of a conductive thin plate according to the principle of virtual work while ignoring the effect of inertia force in middle surface as follows [7]

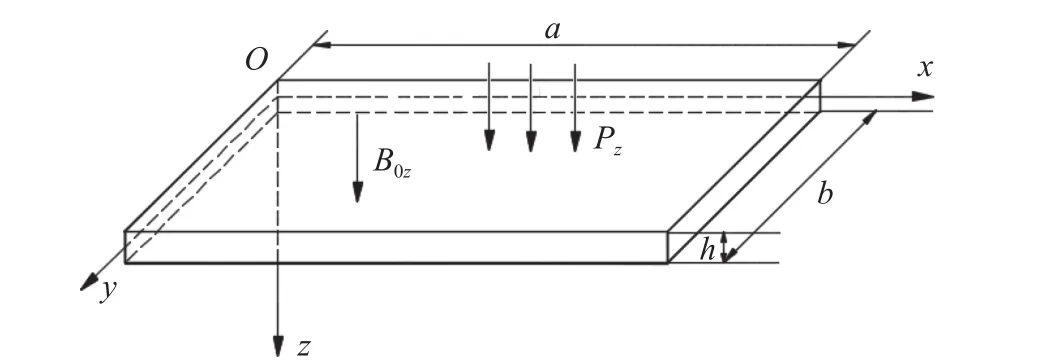
Fig. 1. The model of the rectangular thin plate in transverse magnetic field.

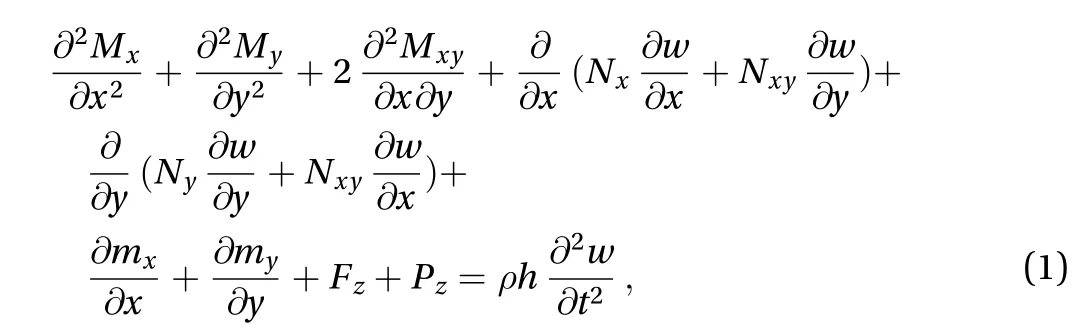
where Nx, Ny, Nxyare in-plane forces, Mx, My, Mxyare bending moments, Pzis mechanical load, Fzis electromagnetic force,mx,myare electromagnetic moments, ρ is the density of the material, h is the thickness of thin plate and t is time variable.

The vector expression of the Lorenz force of thin plate under electro-magnetic field is [24]

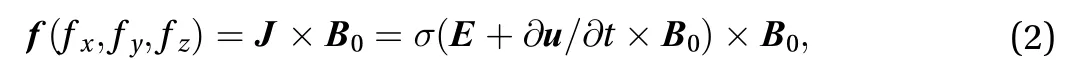
where (Jx,Jy,Jz) is the conduction current-density vector,

(Ex,Ey,Ez)is the electric field vector,0(Bx,By,Bz) is the magnetic induction vector, (ux,uy,uz) is the displacement vector of each internal point of the conductor and σ is the electrical conductivity.

For a rectangular conducting plate subjected to a mechanic dynamic loadPZ=F0cosΩ0t(F0is the amplitude of the exciting force, Ω0is the exciting frequency). Substituting the geometric equations, physical equations and electrodynamics equations [7] into vibration equation Eq. (1), the nonlinear magneto elastic vibration differential equation while ignoring, and the effect of inertia force in middle surface is derived

whereDN=Eh/（1-ν2) is the tensile stiffness,DM=Eh3/[12(1-ν2)]is the flexural stiffness, E is the Young’s modulus, ν is the Poisson’s ratio and the differential operator is

The internal resonance may exist while a rectangular plate satisfies a specific boundary condition. For the rectangular thin plate with one side fixed and the other three sides simply supported, the boundary conditions are x=0, w= ∂w/∂x=0;x=a,w= ∂2w/∂x2=0;y=0,y=b,w= ∂2w/∂x2=0.

Considering the first two modals of system, the displacement solutions which satisfy the boundary conditions can be expressed as follows [25]

Substituting Eq. (4) into Eq. (3), by using the Galerkin method and dimensionless method, the non-dimensional vibration differential equations of rectangular thin plate can be derived as

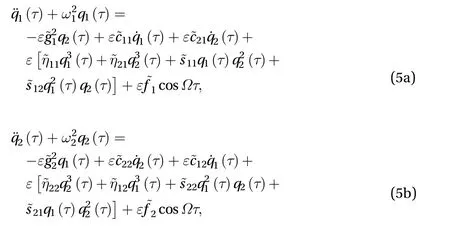
where, ε is a non-dimensional small parameter.

andSji,Kji(i=1,2;j=1,6) have been given in Ref. [23].

Solving the above equation by the method of multiple scales[26] and expressing the approximate solution as

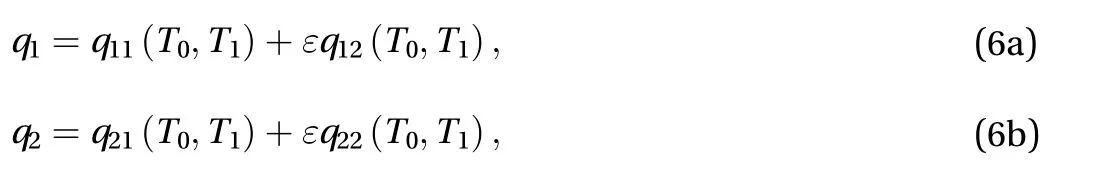
where the time scalesT0=τ andT1=ετ.

Then substituting Eq. (6a) and (6b) into Eq. (5a) and (5b) and equating the coefficients of like powers of ε, the linear partial differential equations of each order are obtained

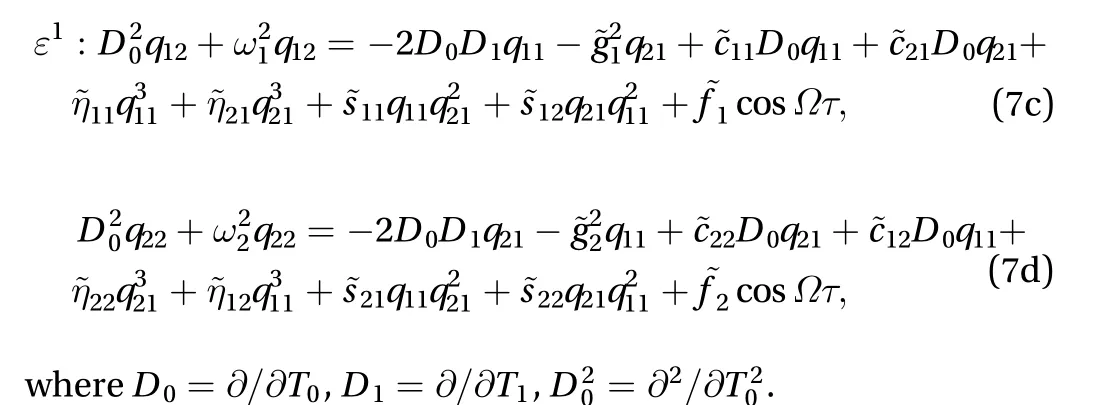
The solutions of Eq. (7a) and (7b) can be written in the plural form [26]

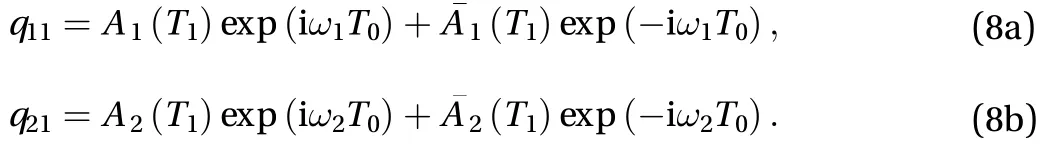
When ω2≈ 3ω1, there is an extra link, or term, connectingq1andq2. This is referred to as an internal resonance. To express quantitatively the nearness of ω2and ω1, here we introduce a detuning parameter σ1and let

When the non-dimensional external excitation frequencyΩ is close to ω1(Ω ≈ ω1), the first mode is directly excited. The system exists the first-order primary-internal resonance. In order to express quantitatively the nearness of Ω and ω1, here we introduce a detuning parameter σ2and let

Substituting Eq. (8a) and (8b) into the right sides of Eq. (7c)and (7d), the secular terms are eliminated fromq12andq22, if

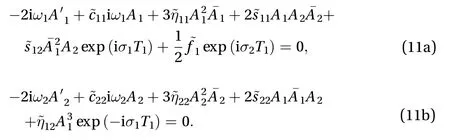
It follows from Eq. (11a) and (11b) that both A1and A2do not decay. The first mode is directly excited by external excitation,though the second mode is not directly excited (i.e.,is not involved in a resonant combination with Ω). The equation governingA2contains the termexp(-iσ1T1) which is a consequence of the internal resonance. That is to say, the second mode which involved with a directly excited mode through an internal resonance is indirectly excited.

We let

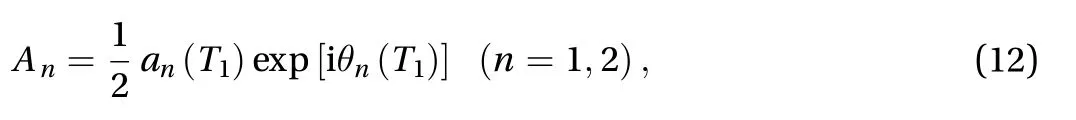
where an(T1) and θn(T1) are the amplitude and phase ofnth mode.

Substituting Eq. (12) into Eq. (11a) and (11b), and separating real and imaginary parts, we obtain the modulation equations

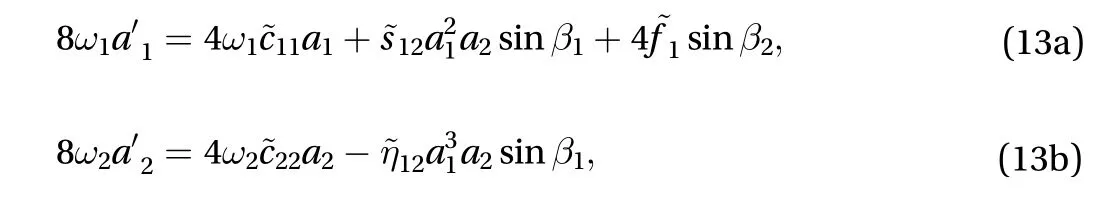
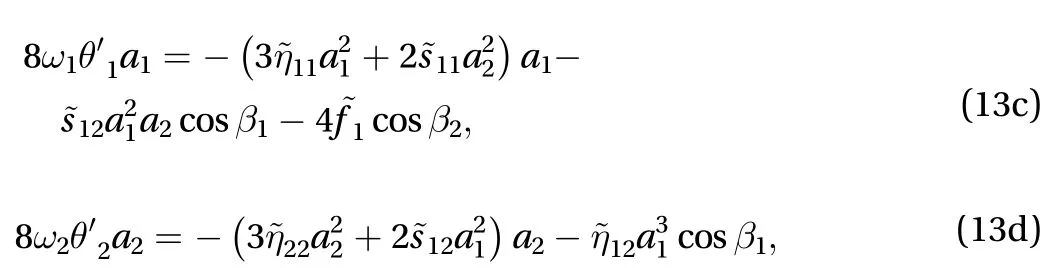
where β1= θ2-3θ1+ σ1T1, β2= σ2T1- θ1.

Then for steady-state motions (a1′=a2′=0 and==0). Hence it corresponds to the solution of

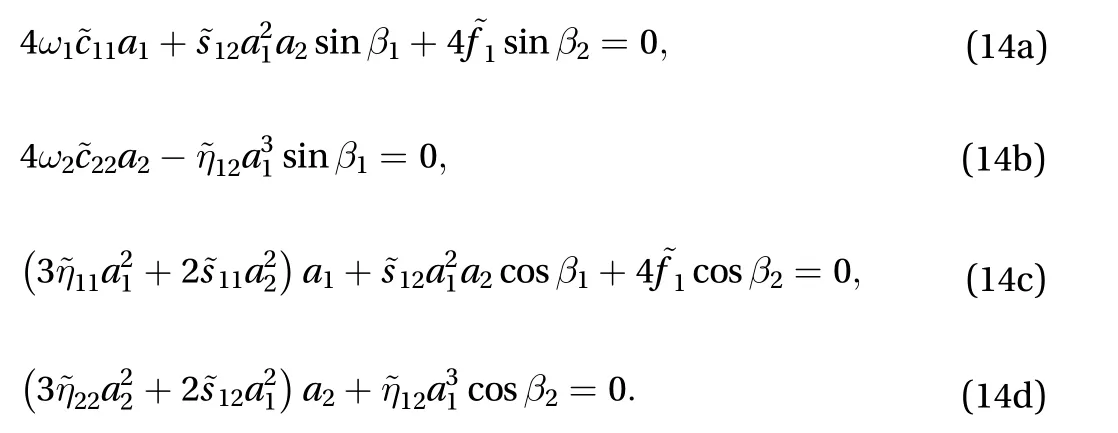
We note that the terms containingin Eq. (14b) and (14d),which are a result of the internal resonance, are similar to the forcing terms in a superharmonic resonance. Hence neithera1nora2can be zero.

For steady-state motions equations, eliminating β1andβ2from Eq. (14a) to (14d) yields

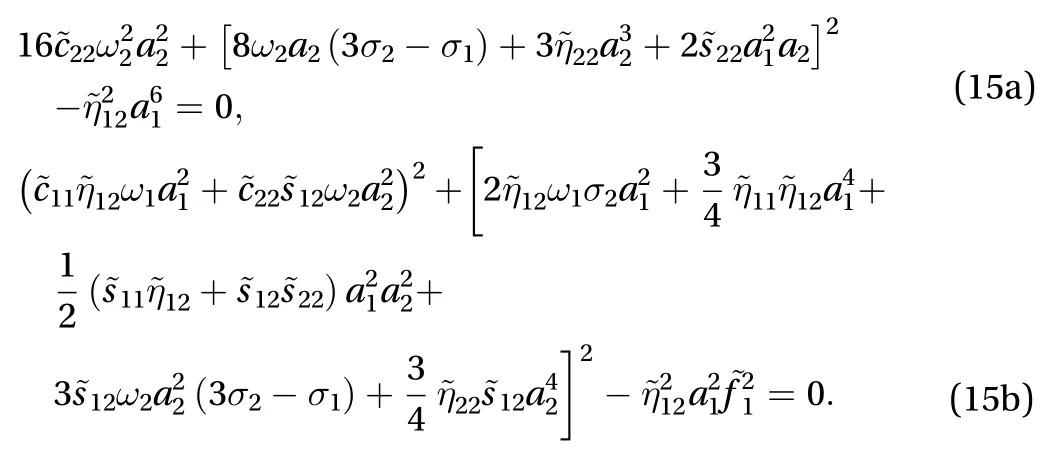
The first approximation the deflection is given by

When the non-dimensional external excitation frequencyΩ is close to ω2(Ω ≈ ω2), the second mode is directly excited. The system exist the second-order primary-internal resonance. In order to express quantitatively the nearness of Ω and ω2, here we introduce a detuning parameter σ3and let

Then the secular terms are eliminated from q12and q22according to Eqs. (9) and (17) if

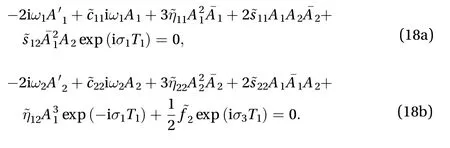
Substituting Eq. (12) into Eq. (18a) and (18b), and separating real and imaginary parts, we obtain the modulation equations

where β1= θ2-3θ1+ σ1T1, β2= σ3T1- θ2.

Then for steady-state motions (a1′=a2′=0 and=0). Hence it corresponds to the solution of

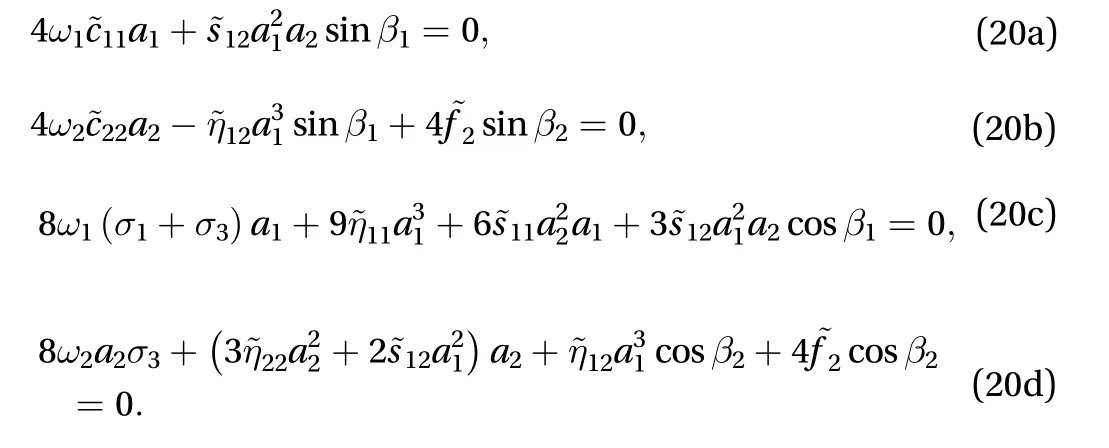
We note that a2cannot be zero, but a1=0 is a possible solution. The terms proportional toin Eq. (20a) and (20c),which are a result of internal resonance, are similar to the forcing terms in a subharmonic resonance. Thus are two possibilities:

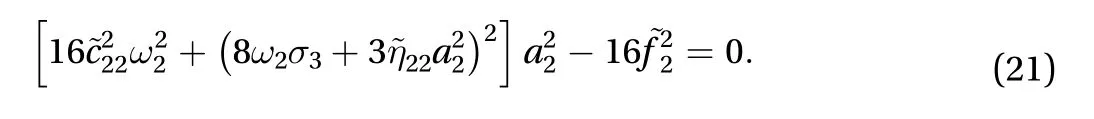
(2) a1/=0 and a2/=0, the equations for amplitudes of the first two modals are

Witha1=0, the first approximation the deflection is given by

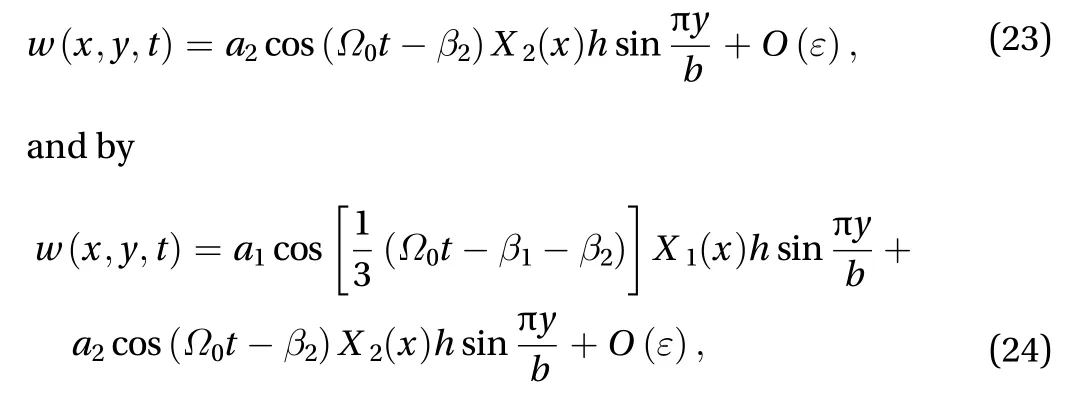
wherea1,a2,andare obtained from Eq. (20a) through Eq.(20d).

Consider a rectangular aluminum thin plate in a constant transverse magnetic field. In Fig. 2, the non-dimensional first two order natural frequenciesand the tripled first order natural frequency 3 ω1are shown as the functions in. This figure enables one to perfectly tune a 1:3 internal resonance whenb/a=2. The main parameters of the aluminum thin plate are given as follows: electrical conductivity is σ =3.63×107(Ω·m)-1, the density isthe Poisson’s ratio is ν =0.34, Young’s modulthe thickness ish=3mm and the two sides of the rectangle area=0.6m,b=1.2m.

Figures 3 and 4 show the amplitude frequency response curves of the first two order modals of system under different external excitation amplitudes for. We note that the first mode and the second mode are both excited, depending on the value of, some curves are single-valued while others are multivalued. With the increase of the amplitude of the external excitation, the effective resonance region becomes wider and the multivalued region is narrow down. The amplitude frequency response of the first mode is similar to that of the single-mode. There is jump phenomena in the curves because of the multivaluedness, and the multivaluedness of the response curves due to the nonlinearity. Although the amplitude of the second mode is not zero, but it is obviously smaller than that of the first mode, the actual response is mainly governed by the first mode. That is to say, although the second mode is coupled with the first mode via internal resonance, the excitation of the first mode does not have a large effect on the second mode.

Figures 5 and 6 show the amplitude frequency response curves of the first two order modals of system under different magnetic field intensities for. When the magnetic field intensity is zero, we can see that the steadystate solutions express complexity, the number of steady-state solutions ofis from one to three and then to five. Furthermore, the maximum amplitudes of the first two modes are approximately equal. With the increase of magnetic field intensity,the maximum value ofdecreases obviously, so the magnetic field has obvious inhibitory effect on the amplitude of the second mode.

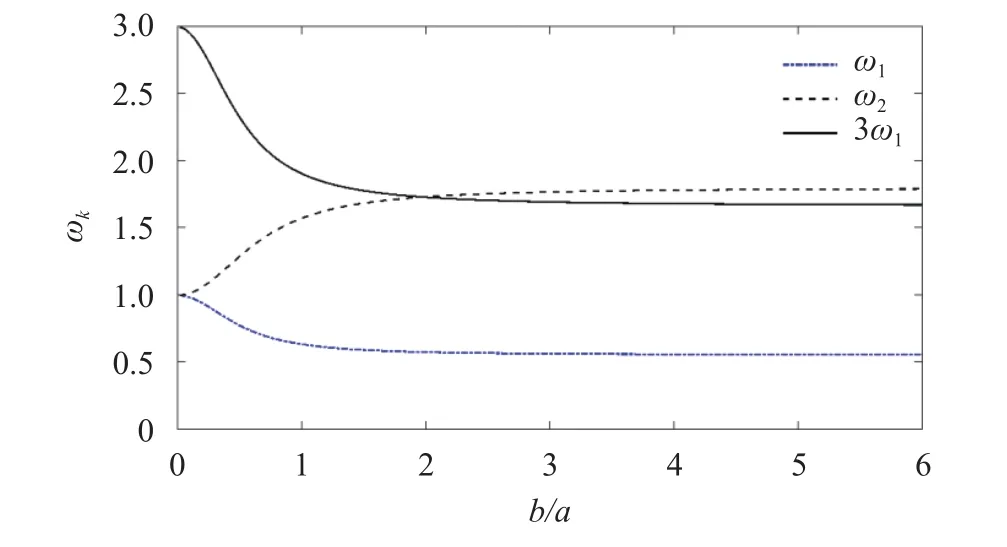
Fig. 2. Variations of the non-demensional frequencies ω 1, ω 2 and 3ω1with b/a.

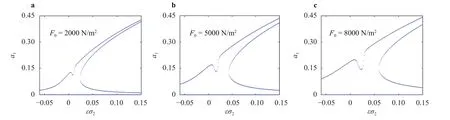
Fig. 3. Amplitude frequency response curves of the first mode under different external excitation amplitudes.

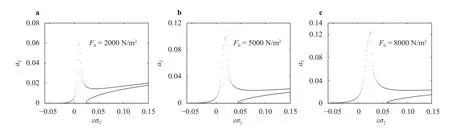
Fig. 4. Amplitude frequency response curves of the second mode under different external excitation amplitudes.

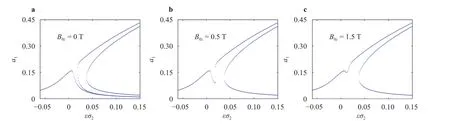
Fig. 5. Amplitude frequency response curves of the first mode under different magnetic field intensities.

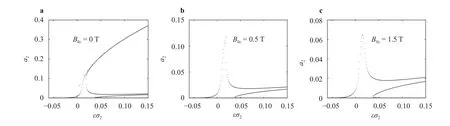
Fig. 6. Amplitude frequency response curves of the second mode under different magnetic field intensities.

Figures 7 and 8 show the amplitude frequency response curves of the first two order modals of system under different ex-ternal excitation amplitudes for. We can note that the first and the second mode can be excited only when the external excitation amplitude exceeds a certain value.With the increase of the amplitude of external excitation, the modal amplitude increases, but when the external excitation amplitude exceeds, the increase of the external excitation amplitude does not cause a significant increase in the maximum amplitude of the first two modes. In this case the second mode is directly excited but the first mode is activated by internal resonance. Furthermore, whenis not zero, it can be much larger than. This means that the internal resonance provides the mechanism for transferring energy down from a high to a low mode.

Figures 9 and 10 show the amplitude frequency response curves of the first two order modals of system under different magnetic field intensities forF0= 5000 N/m2,h= 3 mm.a1is much larger than a2when the magnetic field intensity is not zero. With the increase of magnetic field intensity the modal amplitude decreases and when the magnetic field increases to a certain value, the modal amplitudes will not be excited. It is shown that the magnetic field has an obviously inhibitory action on the amplitude of the first two modes when the higher order mode is directly excited.

For the numerical examples, we solve the dimensionless vibration differential equations Eq. 9(a) and 9(b) by using numerical solving method.

Fig. 7. Amplitude frequency response curves of the first mode under different external excitation amplitudes.

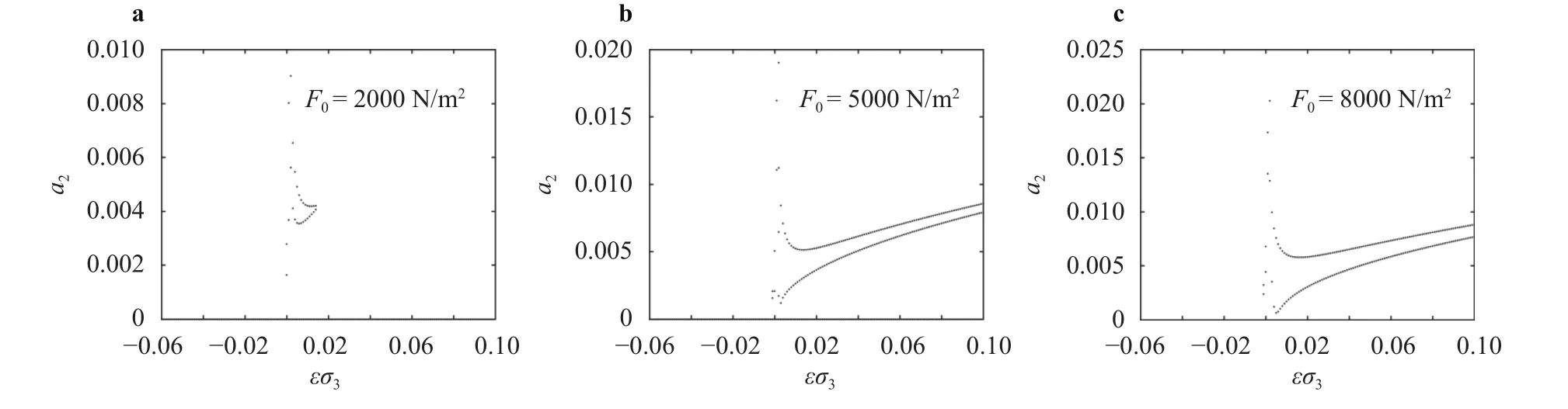
Fig. 8. Amplitude frequency response curves of the second mode under different external excitation amplitudes.

Fig. 9. Amplitude frequency response curves of the first mode under different magnetic field intensities.

Figures 11-13 separately show the time history responses,phase portraits and Poincare maps of the first two order vibration modes of the system under different magnetic field intensities when the first mode is directly excited (,). The following graphs (a), (b) and(c) in Figs. 11-13 are the responses of the first mode which is directly excited by the external excitation and graphs (d), (e), (f) in Figs. 11-13 are of the second mode which is activated via intern-al resonance with the first mode. As a result of the internal resonance, the partial energy of the first mode is shifted to the second mode. From the time history responses, it can be seen that the maximum amplitude of the second mode is only about 1/10 of the first mode, which shows that the response is dominated by the first mode. When(Fig. 14) the phase portrait of the first order mode is a central symmetric multi-circle with boundary, and the Poincare map is a set of points on a closed curve, which exhibits quasi-periodic motion. The phase portrait of the second mode expresses irregular shapes with multi circles, and Poincare is mapped as a set of scattered points with definite geometry, that indicates chaos occurred. When

(Fig. 15) the phase portraits of the first two order modes are annuluses with boundary, and the Poincare maps are the set of points on the closed curve, and the system expresses quasi-periodic motion. And when the magnetic field intensity reaches to(Fig. 16) the phase portraits of the first two order modes are shown as closed circles and the Poincare maps are single points that means the system is expressed as a stable single-frequency periodic motion. The results show that in a certain range of parameter the motion of system transits from chaos and quasi-periodic motion to periodic motion as the magnetic field intensity rises. The modal amplitude decreases because the magnetic field acts as a damping.

In this paper we have investigated the nonlinear vibration of a rectangular conductive thin plate in a transverse constant magnetic field is investigated under the principal and internal resonance. The modulation equations of amplitudes and phase angles of the first mode and the second mode under 1:3 internal resonance are obtained by using Galerkin integral method and multiple scales method. By numerical examples, the amplitude frequency response curves and dynamic response curves of the system via the principle and internal resonance are obtained,and the influence of the parameters such as external excitation amplitude and magnetic field intensity on the vibration characteristics is analyzed. The results show:

Fig. 10. Amplitude frequency response curves of the second mode under different magnetic field intensities.

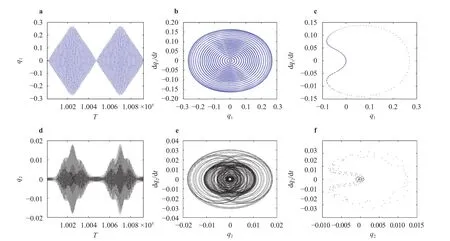
Fig. 11. The response of the system (B 0z=0T): a, d Time history response; b, e Phase portrait; c, f Poincare map.

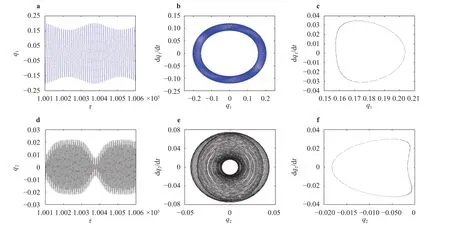
Fig. 12. The response of the system (B 0z=0.5T): a, d Time history response; b, e Phase portrait; c, f Poincare map.

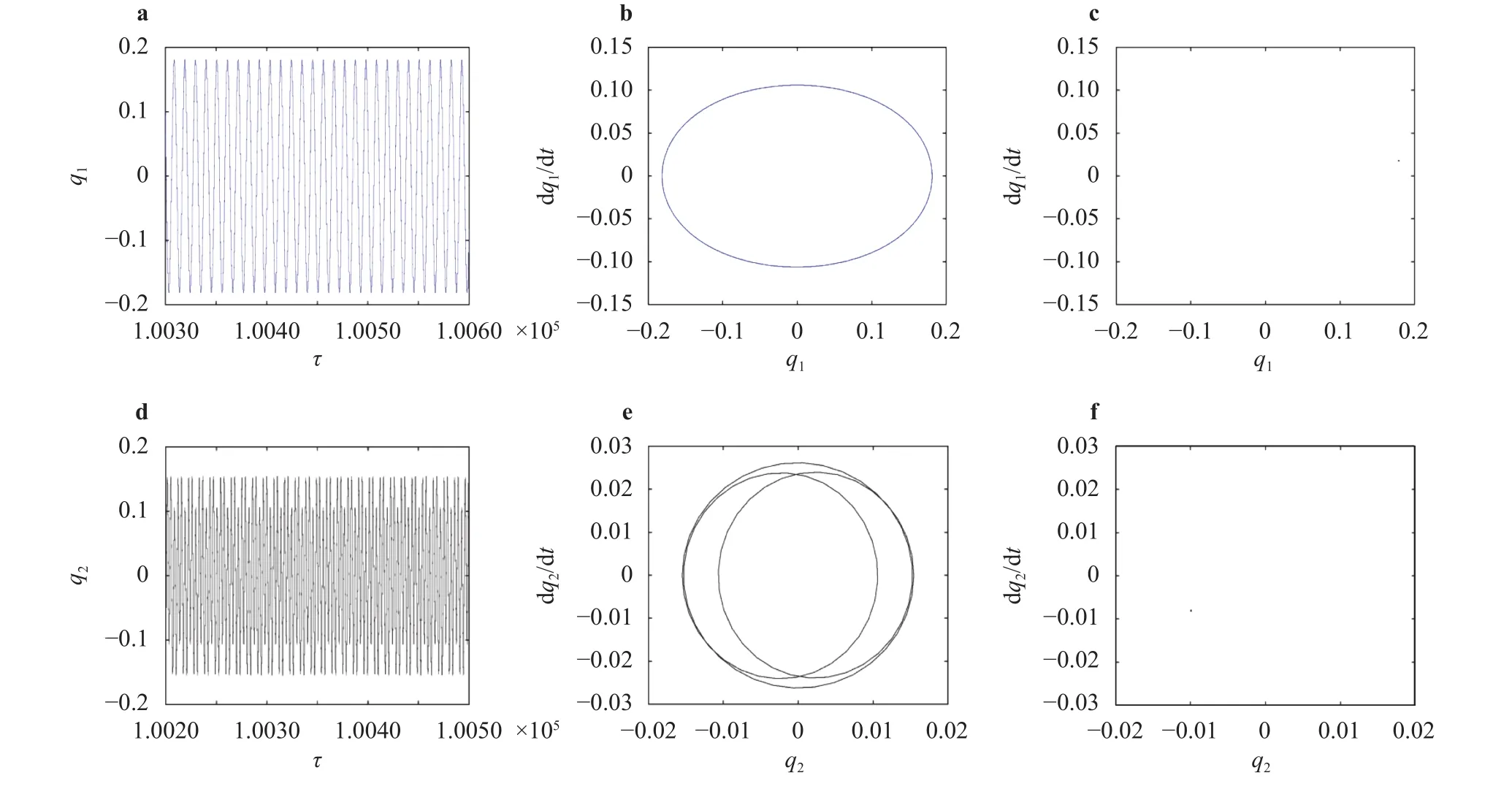
Fig. 13. The response of the system (B 0z=1.5T): a, d Time history response; b, e Phase portrait; c, f Poincare map.

(1) When the first-order primary-internal resonance occurs(the first mode is directly excited), the second mode which involved with a directly excited mode through an internal resonance is indirectly excited. The effective resonance region becomes wider with the increase of the amplitude of the external excitation. The increase of the magnetic field intensity suppresses the amplitude of the second mode. Under certain parameters, the motion of system transits from chaos and quasi-periodic motion into periodic motion with the magnetic field intensity increases gradually from zero, so we can control the dynamics behavior of the system by adjusting the magnetic field intensity.

(2) When the second-order primary-internal resonance occurs (the second mode is directly excited), the amplitude of the external excitation must exceed a critical value before the first mode can be activated. The resonance disappeared if the magnetic field intensity reaches to a certain value. It means that the magnetic field suppresses the resonance.

(3) The response can be dominated by the first mode whether the frequency of the excitation is near the first nature frequency or the second nature frequency. The energy is transferred from a high to a low mode due to the internal resonance.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (11472239) and the Natural Science Foundation of Hebei Province of China (A2015203023).