On the interaction between bubbles and the free surface with high density ratio 3D lattice Boltzmann method

Guo-Qing Chen, A-Mn Zhng*, Xio Hung

a College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China

b School of Marine Science and Technology, Northwestern Polytechnical University, Xi'an 710072, China

Keywords:Lattice Boltzmann method Free energy model High density ratio Multiple bubbles

ABSTRACT The bubbles rise up and burst at the free surface is a complex two-phase process. A free energy lattice Boltzmann method (LBM) model is adopted in this paper to study this phenomenon. The interface capturing technique [Zheng et al., 2006] is used to deal with the high density ratio problem. The Laplace law and the air-water interface capturing ability are validated for the multiphase model. The interaction between the single bubble or multiple bubbles and the free surface are studied by the multiphase model. The force acting on the bubble and the evolution of the free surface is studied. Meanwhile, effect of the initial distance between two adjacent bubbles on interaction effects of multiple bubbles is investigated as well.

Bubble dynamics has become a very important research area in the past few decades. The study of bubbles has great engineering significance and academic value, due to the widely applications of bubbles in pharmacy, marine engineering, environment and aerospace industry etc. [1-4]. Free surface is a common boundary condition for bubbles. And rising bubbles are commonly observed in the process of combustible ice exploitation.Meanwhile, the carbon dioxide gas rising from water and spilling out of the free surface is the main cause of the greenhouse effect. For the case of bubbles rising in liquid, the physical phenomenon of the interaction between bubbles and the free surface is very complicated, which needs to be investigated in detail.

The lattice Boltzmann method (LBM) has a clear physical background and good computational stability and parallelization [5]. These advantages prompt the LBM to be widely adopted in multiphase flow simulations [6-8]. Talada et al. [9] simulated the bubble moves under gravity by using the LBM. Good agreements are reached through comparing with the volumn of fluid (VOF) method. Shi et al. [10] and Alizadeh et al. [11] used the LBM to build up a solid-liquid-gas three-phase coupling model, and studied the translation and deformation of the bubble. Yang et al. [12] and Shan et al. [13] explored the behavior of cavitation bubble collapsing near rigid boundary. And Zhang et al. [14] studied the microcosmic, instantaneous and random cavitation phenomena. Shan et al. [15] investigated the phenomenon of cavitation bubble collapsing between two parallel walls.

The above studies indicate that the LBM is an appropriate method to explore the multiphase flow problem. Nevertheless,there are very few studies focusing on the phenomenon of the interaction between bubbles and the free surface by using the LBM. In this paper, we will briefly introduce the theory and numerical model. And the numercial model is validated by some analytical results and the interaction processes between bubbles and the free surface are simulated, and the conclusion is given at last.

In this paper, the fluid is assumed as incompressible Newtonian fluid with constant temperate. The continuity and momentum equations are the Navier-Stokes equations, and the interface capturing equation is the Cahn-Hilliard equation [16-18],as

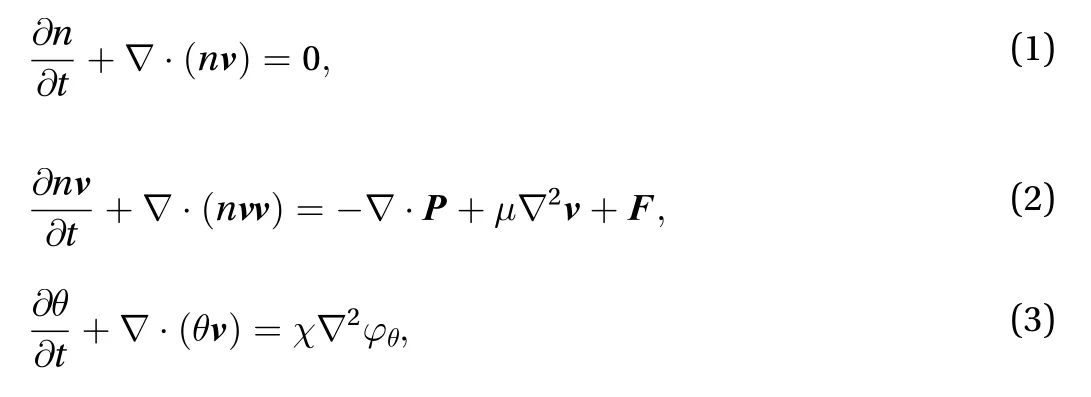
where n=(nA+nB)/2 and θ=(nA-nB)/2 with nAas the density of fluid A and nBas the density of fluid B, respectively[9]. is the fluid velocity, is the pressure tensor, μ is the fluid viscosity, is the body force, χ is the mobility factor, and φφis the chemical potential [19].

The chemical potential comes from the free energy density functional [19, 20], and can be expressed as

whereCand κ are the coefficients related with the phase interaction, θ and θ*are the order parameter and its state in equilibrium,Wis the interface thickness and σ is the surface tension.

Meanwhile, the force ∇ · is written as Eq. (7), which is the function of sound speedcsand the force is relevant to the surface tension force

The lattice Boltzmann method implementation of Navier-Stokes equation [17] and the interface capturing equation [16]can be depicted as

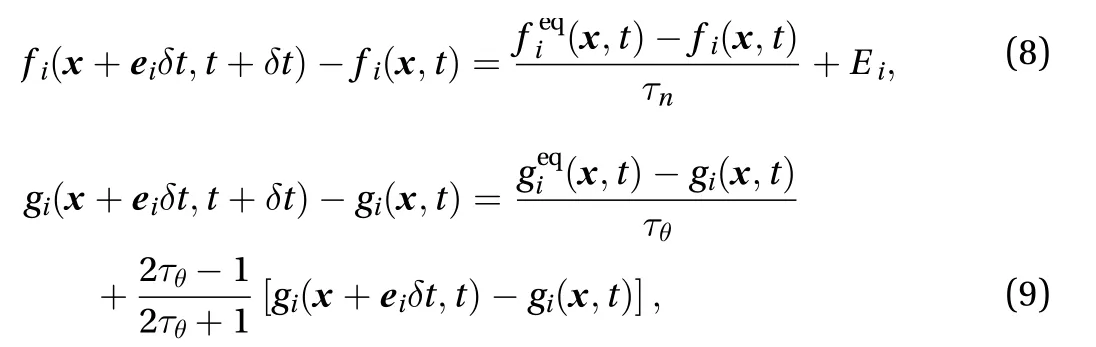
where fiand giare the density distribution function, andandare their state in equilibrium, τnand τθare the single relaxation times,idenotes the lattice velocity vector and δtis the lattice time step.

The nineteen-velocity model (D3Q19) and the seven-velocity (D3Q7) model are adopted in three-dimensional (3D) model, which are proved to have second order precision. And relevant equilibrium distribution functions can be depicted as

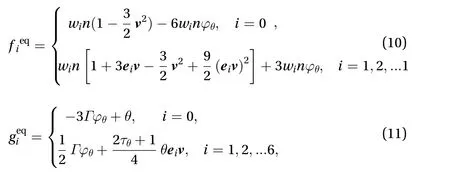
where wiis the weight and Γ is a parameter governing the mobility, as

The termEiincluding the related surface tension termφθ∇θ and the gravity term is desbribed as [21]

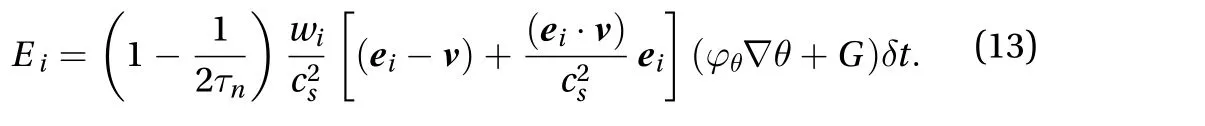
The local macroscopic variables densityn, velocity and the order parameter θ are

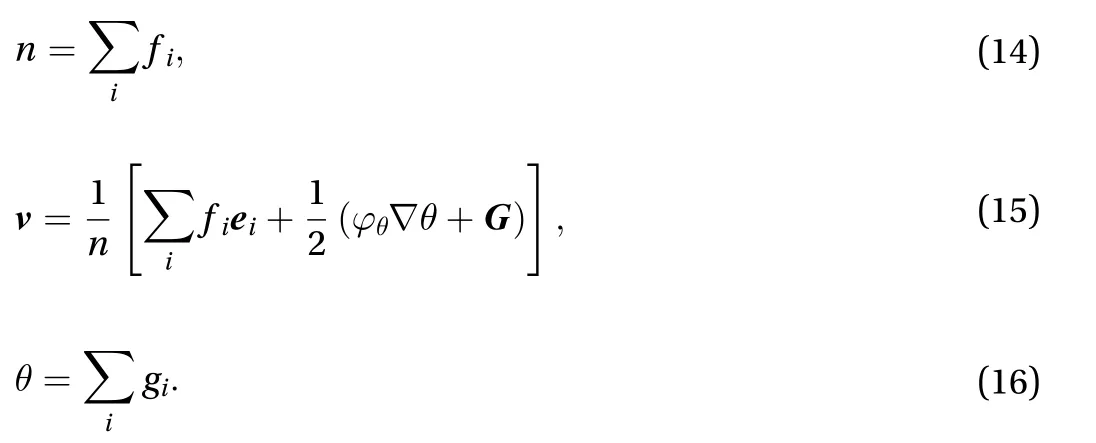
Meanwhile, all variables and parameters are used in the lattice units unless otherwise specified in this work. In order to validate the Laplace law and the interface capturing ability, a stationary bubble is placed in the center of a 3D computational domain. The periodic boundary conditions are applied on all boundaries of the domain. The density of fluid A (water) and fluid B (air) respectively are nA=1000 and nB=1, and the relaxa-tion times are τn=0.875 and τθ=0.7. The governing parameter of the mobility is Γ =100, and the surface tension is.

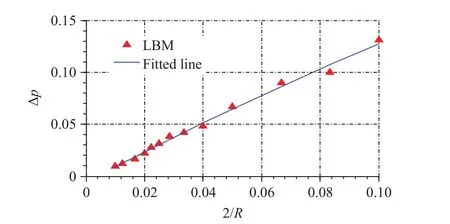
Fig. 1. The relationship between pressure difference across the interface and bubble curvature.

The Laplace law can be described as

where Δp denotes the pressure difference between the two fluids.Ris the bubble radius, which is chosen from 10 to 100 to validate the Laplace law. The pressure difference Δ p across the interface is plotted as a function of the curvature of the bubble in Fig. 1. One can easily see that the Laplace law presents a linear relationship between the pressure difference and the curvature,with a slope of 1.22 as the value of surface tension, which is very close to the surface tensionset above. And the data calculated from the LBM all fall on the analytical line which means that the model built in this work predicts the Laplace law accurately.

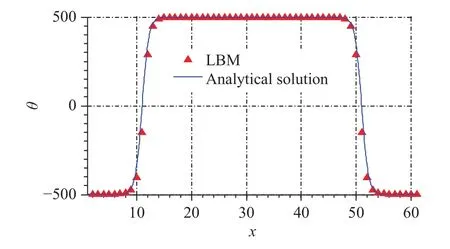
Fig. 2. Value of the order parameter θ with respect to the x position along the horizontal centerline crossing bubble.

The order parameter changing along the normal direction of the interface can be expressed as [18]

Then, we study the phenomenon of single bubble breaking near the free surface. The periodic boundary condition is applied to the walls. And the characteristic velocity (U) , the Reynolds number (Re) and Morton number (M) are defined as

where g is the the gravitational acceleration and μAis the corresponding viscosity.

The surface tension is σ =2.0 and the other coefficients are the same as previous discussion. Meanwhile, we set the computational domain as 90×90×120 and the bubble diameter D=20. The bubble is placed at (45, 45, 50) and the free surface is set at z =70. The process of the bubble rises up and breaks at the free surface is described by the order parameter θ =-250 in Fig. 3.

In Fig. 3, a bubble rises from a stationary state and touches the free surface due to the buoyancy force, and the deformation of the free surface and the upper bubble has occurred before the bubble touches the free surface. Then the effect of surface tension of the air-water interface becomes obvious, and the bubble becomes ellipsoid shape with the influence of the buoyancy force and the surface tension. Meanwhile the free surface is raised with straw-hat shape under the effect of the rising bubble,as shown in Fig. 3(a) to 3(c). Whereafter, the bubble begins to couple with the free surface, and the surfaces of the them break up and fuse together, see Fig. 3(d). Then the bubble continuously rises up and couples with the free surface with the surface broken, due to the effect of gravity, as described in Fig. 3(e). In the end, the bubble fuses with the free surface and forms a circular fusion interface, as shown in Fig. 3(f).

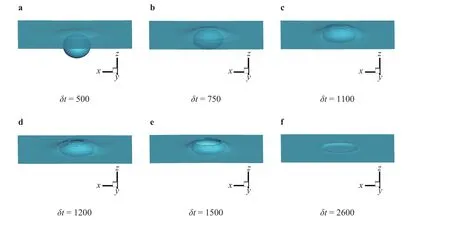
Fig. 3. The process of the single bubble rises up and breaks at the free surface. The dimensionless parameters are R e=9.2 and M =5.0.

Meanwhile the bubble rising velocityuchanging with timetis investigated. The result is given in Fig. 4.

From Fig. 4, we find that the free surface prevents the bubble from rising up, since it impedes the free flow of water above the bubble. In the beginning, the bubble is far away from the free surface, and the buoyancy force is stronger, so the bubble rising velocity u increase with time t. Then the bubble is close enough to the free surface to push the free surface up, the resistance of the free surface to the bubble is stronger. So the rising velocityu of the bubble decreases with timetfor caset≥50.

In the end, the multiple bubbles breaking near the free surface is studied. We define the distance between the centers of two adjacent bubbles asd, and a distance ratio as λ =d/D. The computational domain is 1 10×110×120. The four bubbles are placed symmetrically in the computational domain and other parameters remain the same as the case in Fig. 3. Relevant results are given with the order parameter θ =-250 in Fig. 5.

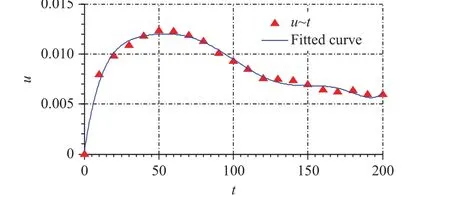
Fig. 4. The bubble rising velocity u changes with time t and the relevant fitted curve.

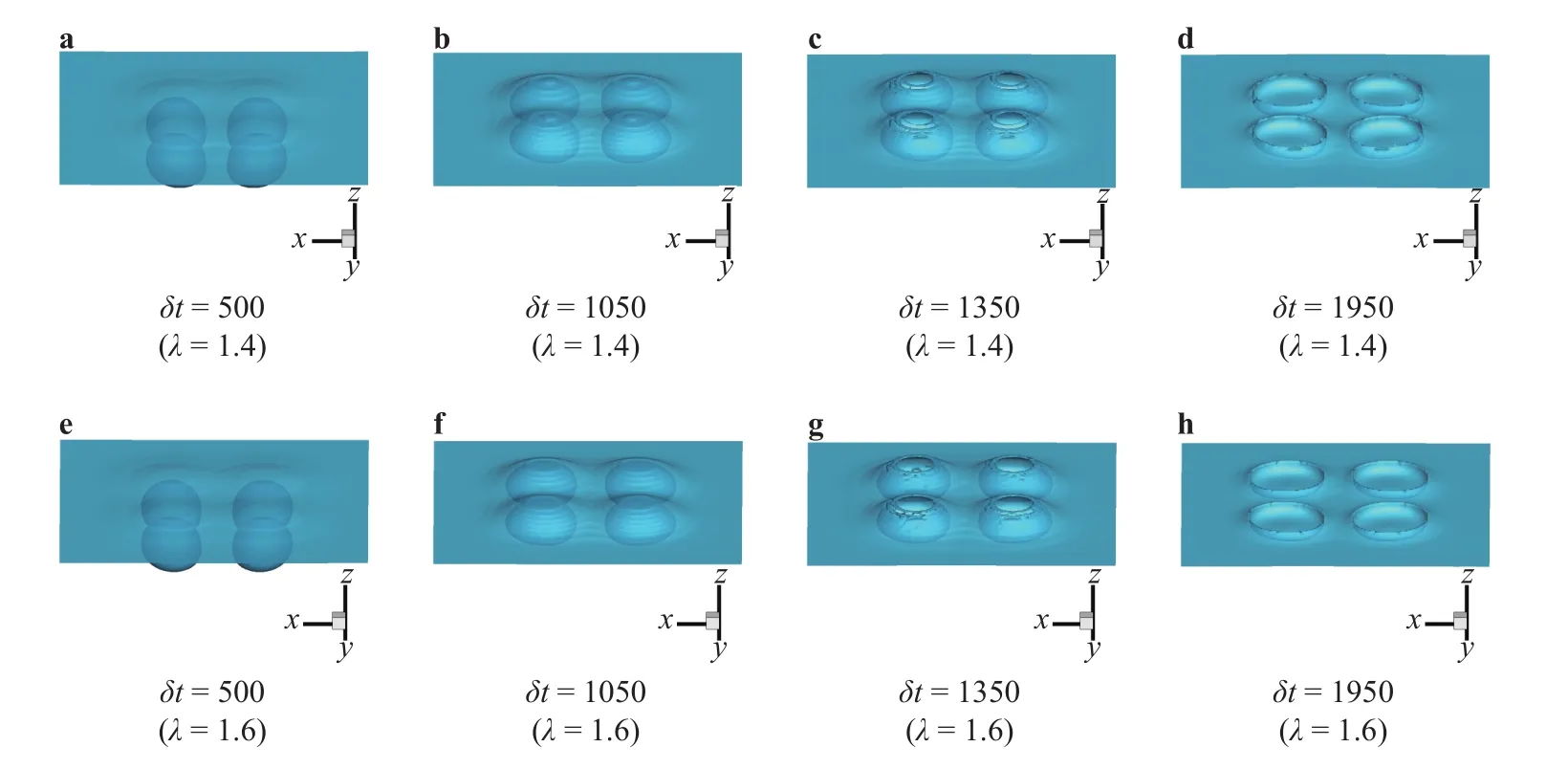
Fig. 5. The process of multiple bubbles rise up and break at the free surface at different distance ratio λ.

The interaction processes of multiple bubbles with the free surface are described in Fig. 5. We found that the bubbles interact with each other, and the degree of influence increases with the decrease of distanced. And bubbles attract each other obviously for the case λ =1.4, which causes the free surface to tilt toward the center of bubbles, as shown in Fig. 5(a) and 5(b).Whereafter, bubbles fuse with the free surface and the free surface break up. Finally, the interaction between bubbles and the free surface is gradually disappeared and the free surface form four elliptic interaction interfaces. Meanwhile, the fusion surface is tilted as well in the whole fusion process, due to the attraction among bubbles, as depicted in Fig. 5(c) and 5(d). When the distance ratiogrows up to 1.6, the attraction between bubbles is small, as shown in Fig. 5(e) and 5(f). Moreover, every bubble has a relatively independent interaction process with the free surface, and interfaces formed by interaction are circular, as described as in Fig. 5(g) and 5(h).

Meanwhile, comparing the cases ofand, we find that the attraction among bubbles strengthens the interaction effect and extents the interaction time. Then we study the relationship between the distance ratioand the interaction time, which is defined as the time from the bubble beginning to rise up to the full fusion of the bubble and the free surface,and find the interaction time T decreases with the distance ratio λincreases as analysis above. Meanwhile, for the case λ ≥1.6,the effect of the attraction among bubbles decreases rapidly. The relevant result is given in Fig. 6

In this paper, the LBM multiphase model in high-density ratio is set up by combining the free energy model of the LBM and the interface capturing technique of Zheng [16]. This multiphase model is used to simulate the bubbles interaction with the free surface.

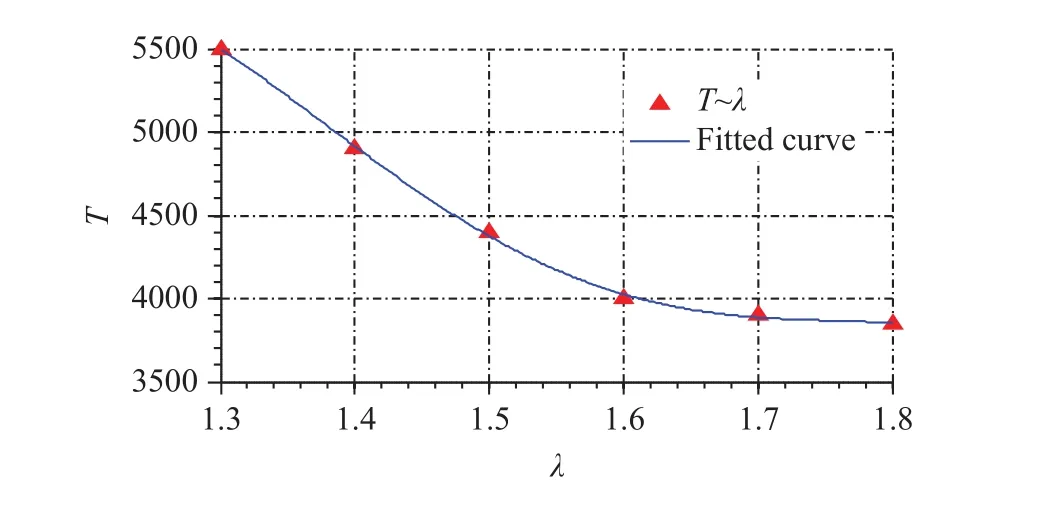
Fig. 6. The relation between the interaction time T and the distance ratio λ with the relevant fitting curve.

The LBM multiphase model satisfies the Laplace law and has good interface capture ability. For the single bubble interacting with the free surface, the free surface is already raised with straw-hat shape before the bubble touches the free surface. Then the bubble and free surface fuses together. Whereafter, the gas inside the bubble is released because of the buoyancy force, and the bubble gradually fuse completely with the free surface. When considering bubbles interacting with the free surface, there is obvious attraction between adjacent bubbles for the distance ratiois the ratio of the center distance of adjacent bubbles to the bubble diameter). In addition, the fusion surface is tilted to the center of bubbles due to the attraction. Moreover,the attraction among bubbles strengthens the interaction effect,forming elliptic the fusion interface and extents the interaction time. Bubbles have a relatively independent dynamic characteristics for case.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (11672081).