Estimation of the effective properties of two-dimensional cellular materials:a review

Federica Ongaro*

a School of Engineering and Materials Science, Queen Mary University of London, London, UK

Keywords:Cellular materials Effective properties Computational homogenization Analytical modelling

ABSTRACT In a vast number of engineering fields like medicine, aerospace or robotics, materials are required to meet unusual performances that simple homogeneous materials are often not able to fulfil.Consequently, many efforts are currently devoted to develop future generations of materials with enhanced properties and unusual functionalities. In many instances, biological systems served as a source of inspiration, as in the case of cellular materials. Commonly observed in nature, cellular materials offer useful combinations of structural properties and low weight, yielding the possibility of coexistence of what used to be antagonistic physical properties within a single material. Due to their peculiar characteristics, they are very promising for engineering applications in a variety of industries including aerospace, automotive, marine and constructions. However, their use is conditional upon the development of appropriate constitutive models for revealing the complex relations between the microstructure's parameters and the macroscopic behavior. From this point of view, a great variety of analytical and numerical techniques have been proposed and exhaustively discussed in recent years. Noteworthy contributions, suggesting different assumptions and techniques are critically presented in this review paper.

1 Introduction

It is well known that nature has developed a large number of ingenious solutions that served as a source of inspiration for scientists and engineers [1, 2]. In the literature, many works discuss this aspect. Among others, the pioneering textbook by Thompson [3] or, more recently, by Mattheck and Kubler [4],where the authors extracted engineering principles from the structure of trees. Nowadays, terms like biomimetics or bioinspiration [5-7] are commonly used to describe the new approach in chemistry, material science and engineering. That is, researchers study biological systems to find some useful principles to create and/or improve new materials and simplify many of our dayto-day functions. Indeed, lessons learned from nature solved a variety of technical challenges in material science [8], architecture [9], aerodynamics and mechanical engineering [10]. For instance, most are familiar with the Velcro, inspired by the way plant's burrs stuck to animal's fur [11, 12], with the high performance swimsuits, modelled on the structure of shark's skin to re-duce drag in water [13], or with the super adhesive fabrics that mimic the configuration of the gecko's foot [14].

Differently from the engineer, nature has a limited number of polymeric (e.g. proteins or polysaccharides) and ceramic (e.g.calcium salts or silica) components to choose. However, despite this limited toolbox, nature assembled an astounding range of structures, perfected over millions of years of evolution, that are able to combine the desirable properties of their building blocks and, often, perform significantly better than the sum of their parts [15, 16]. In most cases, the resulting systems offer unique combinations of mechanical properties that, in man-made materials, tend to be mutually exclusive. Bone and nacre, for instance, are natural materials that combine strength and toughness at low weight, a distinctive quality that synthetic structural materials are still far from achieving. Indeed, strong materials are invariably brittle, whereas tough materials are frequently weak [15, 17]. Other examples include bamboo and palm, two highly porous materials whose exceptional structural efficiency,in terms of mechanical performance per unit weight, fascinated a lot of scientists and engineers [18, 19]. Such plants, in particular, are equally light, strong and flexible, three characteristics that in engineered materials difficulty coexist: when high porosity is needed, it is usually at the expense of mechanical stability.Contemporary characterisation and modelling tools allowed researchers to begin deciphering the intricate interplay of mechanisms that endow natural systems with their unusual properties. Unfortunately, identifying the salient strategies providing the astonishing combinations of stiffness, strength and toughness at low weight, is not a trivial undertaking and it is an open question how nature succeeded in doing this. Some authors,however, analysed different types of natural materials and, after finding common design themes among them, suggested that the superior traits of natural structures stem from their complex hierarchical architecture spanning from the molecular to the macroscopic scale, in conjunction with the confluence of mechanisms that interact at multiple length scales. Hierarchy, in particular, allows the organism to be multifunctional and, through the optimisation of its architecture at each structural level, to perform both biological and mechanical functions to the best of its abilities [1]. That is to say, a specific property can be tuned at different levels, independently of other parameters, and adapted to the local needs [20, 21]. The aforementioned bamboo, for example, is a hierarchical fibre-reinforced cellular material,composed of parallel cellulose fibres embedded in a ligninhemicellulose matrix shaped into honeycomb-like cells [18]. The feature responsible for the high efficiency of the plant, in terms of flexural rigidity per unit weight, in the not-uniform distribution of the load-bearing fibres across the numerous length scales, in addition to a not constant cell walls' thickness. The plant, in particular, creates a gradient of density and modulus of fibres, with higher values of density where the stresses are larger[15]. This solution leads to an optimised hierarchical architecture where the plant, to perform its functions, at each structural level uses the smallest quantity of the most highly efficient cell walls' material. In other words, it can be said that, under a considerable number of constraints, every structural level is a local design optimum.

In their most sophisticated form, natural systems are even able to adapt their configuration to the changing mechanical environments [22]. One example is the vegetative parenchyma tissue [2, 23-26], composed by a network of thin-walled polyhedral cells filled with a fluid. The latter, due to the hydrostatic pressure exerted against the cell walls, significantly improves the resistance of the cells and, consequently, of the whole tissue. The parenchyma, because of its low relative density, is found in many natural systems, as the leaves of monocotyledon plants, irises and maize. In this case, the parenchyma constitutes the lightweight inner core of the leaf and, similarly to an elastic substrate, supports the dense and strong fiber-composite outer faces. Recent studies [23, 27, 28] reveal that this composite solution, notwithstanding the low mechanical properties of the parenchyma, makes the leaf more performant in terms of bending and buckling resistance. Another composite configuration can be found in the hygroscopic keel tissue of the ice plant Delosperma nakurense. The ice plant grows in the arid regions of Africa and, to prevent the premature dispersion of the seeds,produced a special seed capsule where, in the dry state, five petal-like sections, the protective valves, cover the seed compartment as a box-like lid. When it rains, the valves, unfolding backwards, reveal a seed compartment partitioned in five seed chambers from which, within few minutes, most of the seeds are splashed out by the falling water [29]. Then, when the capsule dries up, the valves return to the original position. The specialised organ promoting this sophisticated origami-like movement mechanism for seed dispersal is the hygroscopic keel tissue characterised, in the dry state, by a honeycomb structure having the internal volumes of the elongated cells filled with a swelling cellulosic inner (CIL). Due to the high adsorption and desorption capability of the CIL, the influx/efflux of water into the cells leads to a volume increase/decrease of the CIL, resulting in cells having the ability to open and close upon wetting/drying cycles.It follows a reversible change in the original geometry and stiffness of the whole tissue, that is thus able to combine load bearing and morphing functions [30-32]. Referring the interested reader to Refs. [33-36] for a systematic and comprehensive review on the principles of reversible plant movements, it can be said that such adaptive systems, able to autonomously alter their external shape, can advance the state of the art of many applications. For example, high performance aircrafts can benefit from integrative morphing wings to control their flights paths without sacrificing the aerodynamic streamline and fuel economy [37].Also, kinetic architectures capable of altering their internal configurations can provide extra freedoms for indoor environment control and human-building interaction [38]. Finally, sensing devices and soft robots can exploit the shape changing materials for miniaturisation [31].

Up to date, the most investigated biological systems are cellular materials. Commonly observed in nature, cellular materials offer useful combinations of structural properties at low weight, as in the case of the previously mentioned parenchyma tissue. Wood, bone, tooth, mollusk shells, crustacean and many siliceous skeleton species like radiolarians, sea sponges and diatoms [39], also benefit from the peculiar characteristics of biological cellular structures. From a geometric point of view, at mesoscopic scale cellular materials are discrete materials characterised by a more or less clearly distinguishable architecture and they can be conceived as generated by tessellating a unit cell, a concave space bounded by edges or solids faces,throughout the space. People have used natural cellular materials for millennia; wooden artefacts have been found in the Egyp-tian pyramids and cork has been used for the soles of shoes since Roman times [40]. Today, the structure of natural cellular materials is mimicked in engineering honeycombs, where the cells are obtained by extrusion of planar faces, and foams, where the cells are polyhedra packed in the three-dimensional space. Because of their unique properties arising from the cellular architecture,honeycombs and foams are very promising for engineering applications in a variety of industries including aerospace, automotive, marine, and constructions [3, 41, 42]. For instance, the low density makes them ideal core materials in lightweight and high-performance sandwich panels used in aerospace components and sporting equipment. The low compressive strength and the high deformation capacity provide excellent shock mitigation and energy absorption characteristics in impulsive phenomena. Finally, small cells and low volume fraction lead to closed-cell foams that are excellent thermal insulators.

In addition to the relative density, defined as the ratio of the density of the cellular solid to the density of the cell walls, two sets of parameters affect the mechanical behavior of honeycombs and foams. The first characterises the constituent material while the second is related to the geometric and topological properties of the microstructure. Many authors focused of the mechanical modelling of cellular materials in order to derive their effective properties. Different assumptions and techniques have been proposed in the literature and the aim of this review paper is to critically present the main contributions and to offer the reader an extended list of references. The manuscript is organised in 5 sections, including this introduction. Initially, Sect.2 provides the basic theoretical tools to understand the mechanics of two-dimensional cellular materials, topic of the present paper. Then, in Sect. 3, the pioneering results of Gibson and Ashby [40] are reported, together with the results obtained by applying the structural analysis- and energy equivalence-based techniques to estimate the effective behavior of traditional and advanced cellular materials. An overview of the computational homogenization approach can be found in Sect. 4, where a practical example is also provided. Finally, Sect. 5 concludes the paper.

2 Two-dimensional cellular materials: overview and basic theoretical tools

2.1 Cell shape

Honeycombs (or planar lattices) are generated by tessellating a polygon to fill the plane without gaps or overlaps, and such that neighbouring polygons share full edges and have coincident vertices. Also, angles meeting at one vertex sum up to.Classically, honeycombs are classified as regular, semi-regular or irregular [43]. In the first case, the tessellation is composed by a single type of regular polygon, the square, the triangle or the hexagon, while the second is based on two or more kinds of them. In particular, only eight semi-regular tessellations exist[44, 45]. An example, sketched in Fig. 1(c), is the triangularhexagonal lattice, known as the Kagome. Finally, the irregular tessellations are constructed from two or more irregular polygons of different size, like the random Voronoi lattice [40] or the Penrose tiling [46].

In addition to the previously described configurations, an interesting class of non-conventional lattice materials having unusual properties, like a negative Poisson's ratio [47, 48] or a negative dynamic bulk modulus [49], have been recently introduced: chiral honeycombs. Chiral structures consist of circular elements of constant radius, acting as nodes, linked to each other by straight ligaments tangent to the nodes and, as illustrated in Fig. 2 can not be mapped to the corresponding mirror image by rotations and translations only [50, 51]. Different types of chiral lattices can be obtained just by changing the spatial arrangement of the nodes and ligaments. For example, related to the number of ligaments connecting each node, trichiral, tetrachiral and hexachiral lattices exist, possessing, in turn, 3, 4,and 6 ligaments and derived, respectively, from the classical hexagonal, rectangular and triangular lattice (Fig. 2). In addition,connecting adjacent nodes by the same side of the ligament,provides the anti-chiral lattices that, depending on the number of linking elements, are classified as anti-trichiral, anti-tetrachiral and anti-hexachiral having, on order, 3, 4 and 6 ligaments.

2.2 Stretch and bending-dominated lattices: the role of nodal connectivity

From a geometric point of view, a two-dimensional cellular material can be described as a number of vertices, Nv, joined by edges, Ne, surrounding cells, Nc, related by the Euler's law [40]

The number of edges that meet at a vertex, definednodal connectivity,Ze, can be expressed by

since each edge connects two vertices [40]. The hexagonal,square and triangular lattices have, respectively,and.

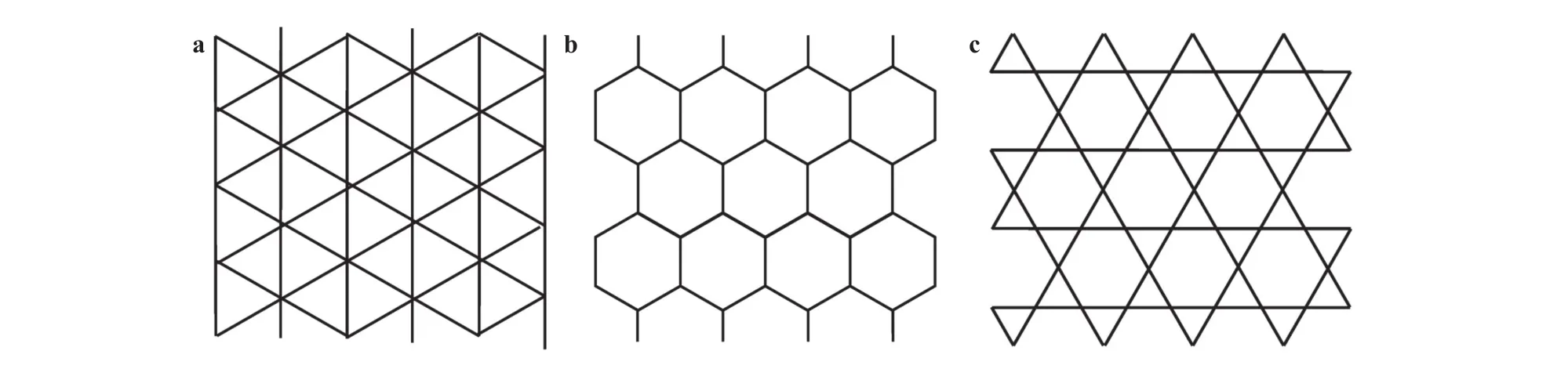
Fig. 1. The regular a triangular and b hexagonal lattices; c the semi-regular Kagome tessellation.

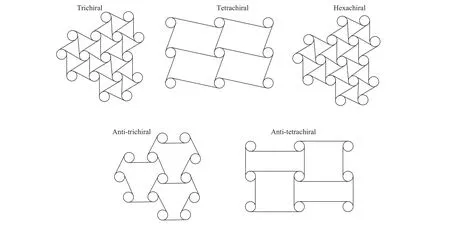
Fig. 2. Chiral and anti-chiral honeycombs.

The macroscopic properties of a honeycomb are strongly affected by its nodal connectivity rather than by the regularity of its microstructure. The reason is related to how the honeycomb responds to macroscopic loads, that is to say with a bending- or stretch-dominated behavior. The distinction of a bending- and a stretch-dominated lattice, exhaustively described in Ref. [43], is connected to the collapse response of a pin-jointed frame of the same morphology. If the parent pin-jointed frame has either no collapse mechanism or only a periodic collapse mechanism that do not produce macroscopic strain, the welded-joint version(the lattice itself) is stretch-dominated. Conversely, when the parent frame exhibits collapse mechanisms that generate macroscopic strain, the welded-joint structure is bending-dominated.

From a mathematical point of view, the above considerations are a consequence of the Maxwell's criterion,

establishing a necessary condition for a planar pin-jointed frame made up ofstruts andfrictionless joints to be statistically and kinematically determinate, namely, a just rigid framework[52]. If the frame has less struts, it will behave as a mechanism and, if loaded, it will collapse. Conversely, if the frame has more struts, it will be overconstrained. By applying the Maxwell's rule to the case of a large pin-jointed framework of nodal connectivity, Fleck et al. [43] concluded thatis a necessary, but not sufficient, condition for rigidity in the twodimensional space. The authors also suggested two classes of planar pin-jointed frames according to their connectivity(Fig. 3). The first, with, are the rigid structures that possess no collapse mechanisms and, if loaded, their members carry tension or compression, as in the case of the highly redundant triangulated configuration having. The same mechanical behavior is observed in the corresponding weldedjoint version, resulting in a stretch-dominated lattice whose effective mechanical response is governed by the axial stiffness of the members [43,53]. In the second class of pin-jointed frames, with, the structures are not rigid and, depending on the direction of the applied external load, collapse by periodic mechanism or by macroscopic strain-producing mechanism. This leads to a welded-joint lattice that, based on the direction of the load, manifests a stretch- or a bendingdominated behavior. In the latter case, in particular, locking the joints cause the struts to bend and the mechanical response of the resulting lattice is dominated by the bending rigidity of its walls and by the rotational stiffness and strength of the nodes.An example, illustrated in Fig. 3, is the hexagonal microstructure,, being stretch-dominated if loaded precisely parallel to the axis of the hexagons, bendingdominated in the other circumstances. The boundary caseis very special and includes both stretch- and bendingdominated structures. The Kagome microstructure, for example,is rigid in all directions and only collapses by periodic mechanism that do not produce macroscopic strain. Conversely,the triangular-triangular topology exhibits a macroscopic strainproducing mechanism. Consequently, the corresponding welded-joint lattices are classified as stretch-dominated, the first, and bending-dominated, the second. Finally, the square pin-jointed frame collapses by periodic mechanism when the applied load is aligned with the walls, by strain-producing mechanism if loaded in the diagonal direction. Thus, the welded-joint lattice is, respectively, stretch- and bendingdominated. A detailed description, that is beyond the scope of the present paper, can be found in Ref. [54], where the authors present a methodology based on the Bloch-wave analysis to explore the collapse mechanism of different structures.

Finally, in terms of mechanical efficiency, one key findings of[55] is that the specific stiffness and the specific strength of the stretch-dominated structures are higher than those in which the dominant mode of deformation is by bending, being, as stated,the mechanical response relying, respectively, upon the axial and upon the bending stiffness of the members. To make it more clear, let us consider the following scaling laws, obtained by Gibson and Ashby [40, 43] by applying the standard beam theory to investigate the mechanical behavior of the lattice material (cf.Sect. 3.1):

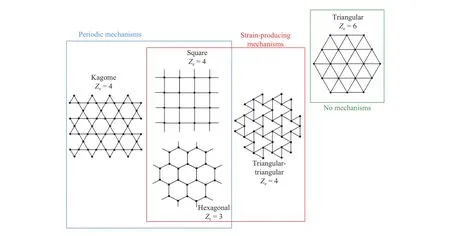
Fig. 3. Venn diagram classifying two-dimensional periodic pin-jointed frameworks according to their collapse mechanism (modified from Ref.[43]).

According to the above equations, the relative stiffness,, and the relative strength,, of the lattice, defined, in turn, as the ratio of the effective stiffness, E , and effective strength, σ, of the lattice to the stiffness, Es, and strength, σs, of the constituent material,can be expressed as a function of the relative density ρ¯, given by the ratio between the density of the lattice and of the solid. For a lattice material, ρ¯ is closely related to the thickness, t, and length, ℓ, of the walls via the relation

withAa constant of proportionality depending on the geometry of the structure. Regarding the constantsBandCin Eq. (4),their typical values are on the order of 0.3 to 0.5 and, similarly toA, depend upon the geometry of the lattice. For example, the triangular, hexagonal and Kagome lattices illustrated in Fig. 1 have, on order, [43]

In contrast, the exponentsbandcare related to the mechanical behavior of the lattice, being b =1 and c =1 for the stretchdominated structures, b=3 and c=2 for the bendingdominated ones, leading to [43]

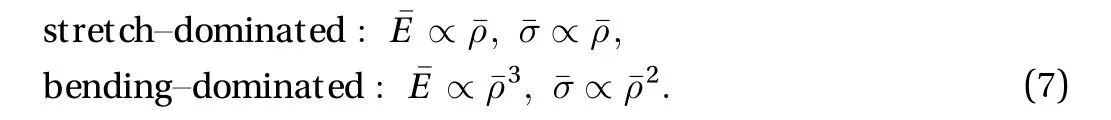
Considering that for a lattice material ρ¯ is usually less than 0.2[40], it follows that a stretch-dominated topology is stiffer and stronger than a bending-dominated one, respectively by a factor of 3 and a factor of 2. For completeness, it should be noted that analogous considerations still apply in the case of threedimensional foams. For an in-depth explanation, the interested reader is remitted to [43] and the references therein.

2.3 Honeycomb mechanics

Figure 4 illustrates the compressive stress-strain curves of a honeycomb subjected to in-plane loads: Fig. 4(a) in the case of a bending-dominated structure and Fig. 4(b) in the case of a stretch-dominated one. As it can be seen, there are generally three zones. Firstly, a linear elastic regime corresponding to the bending, Fig. 4(a), or stretching, Fig. 4(b), of the cell walls. Then,a stress plateau where the cells progressively collapse at a nearly constant stress by elastic buckling, plastic yielding or brittle crushing. Finally, at high strains, a regime of densification in which a great number of cells are collapsed, their opposite walls impinge and further deformations compress the constituent material itself. In terms of deformations, in the linear-elastic regime they are homogeneous throughout the specimen and, as in ordinary solids, the Hooke's law can be applied. Conversely, in the plateau regime the deformations are strongly localised, with the formation of bands perpendicular to the loading direction.

In the present paper, only the linear-elastic behavior is considered.

Fig. 4. A schematic compressive stress-strain curve for a bending-dominated and b stretch-dominated structures, modified from Ref. [40].

3 Continuum modelling of cellular materials: prior works and subsequent developments

As stated in Sect. 1, cellular materials have a great variety of engineering applications. In most cases, their use serves macroscopic purposes so that a continuum description in terms of effective mechanical properties is of importance.

Generally, in understanding how a homogenized medium can "substitute" a heterogeneous material, it is implicitly assumed that the problem contains two well-separated scales.Namely, the microscopic scale (or local scale), small enough to clearly identify the heterogeneities, and the macroscopic scale(or overall scale), where the heterogeneities can be sweared-out[56]. At the macroscopic scale, the effective properties of the composite can be derived from the geometric and mechanical parameters of the microstructure. However, analysing large size volumes on a microstructural level to gain an accurate estimation of the local fields is unsuitable and, in some cases, may involve considerable efforts. Thus, the notion of representative volume element (RVE) or unit cell is of paramount importance and we will come back to it later in the paper. Usually, the RVE is regarded as a volumethat is sufficiently large to include a sampling of all microstructural heterogeneities and sufficiently small to be considered as a volume element of continuum mechanics [57]. Then, through a RVE-based analysis, the necessary microstructure's parameters are extracted and, according to the homogenization procedure, both the RVE of the real system and the corresponding volume element of the equivalent homogeneous continuum, if deformed, are assumed to be subjected to the same stress, strain or energy fields [58]. Finally, from a conventional analysis at the macroscopic level, the information are then transferred between the micro (RVE) and the macro (equivalent continuum) scales and the constitutive model for the homogenized material can be obtained. Although much debate has taken place on what constitutes an appropriate definition of the RVE,in investigating cellular materials the repetitive unit cell of the tessellation is generally assumed as RVE [59, 60] and the hypothesis of global periodicity (i.e., macroscopic medium obtained by a periodic repetition of the unit cell) is made. In addition, regarding the crucial passage from the microscopic discrete description to the coarse continuous one, energy equivalence concepts and micro-macro relations in terms of forces and displacements are usually applied. Finally, linear elasticity and material isotropy, in conjunction with the underlying microstructure assumed to be governed by the classical beam theory [68], are three commonly used simplifications that provide explicit stressstrain relations and help clarifying the basic mechanical aspects[61].

Many authors extensively studied the mechanical characterisation of cellular materials using analytical and numerical models [40, 62-67] and it would be difficult to quote without omissions the vast literature flourished in the last years. Noteworthy contributions, suggesting different assumptions and techniques,are presented in the following sections. For the interested reader, the suggested references can be supplemented with the reviews proposed in Refs. [69-71], concerning the mechanical behavior of honeycombs and of both liquid and solid foams. The technical aspects regarding the analysis of structural lattices and the derivation of their equivalent constitutive equations are throughly reviewed in Refs. [72, 73], where an extended list of references is also provided.

3.1 The pioneering contribution of Gibson and Ashby

The most known and widely used micromechanical model is theGibson and Ashby's model[40, 63, 74] that focuses on the deformation mechanism of a single cell subjected to different types of external loads: uniaxial compression in the horizontal and vertical directions (Fig. 5(b)), pure shear (Fig. 5(c)).

By assuming infinitesimal strains and applying the standard beam theory, the authors obtained simple power-law relations between the microstructure's parameters and the macroscopic properties of a wide range of cellular materials. For example, in the case of a hexagonal honeycomb, the in-plane elastic constants are expressed by

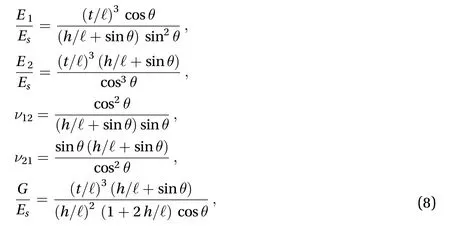
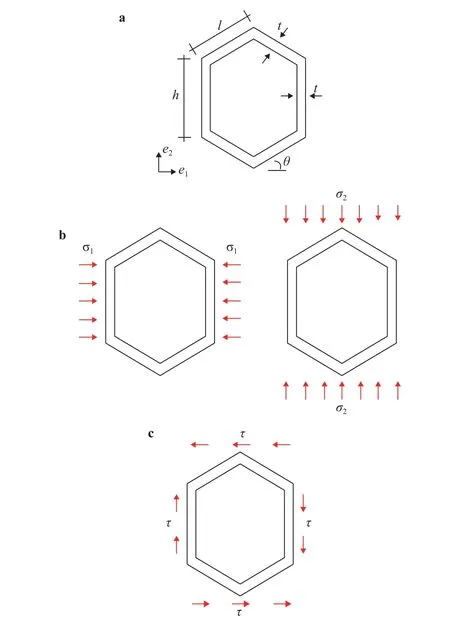
Fig. 5. The unit cell in the Gibson and Ashby's model: a geometric parameters, b uniaxial compression forces in the horizontal,, and vertical, σ2, directions, c shear forces,.

withE1, ν12and, respectively, the effective Young's modulus and corresponding Poisson's ratio in the1anddirection, G the effective shear modulus, Esthe Young's modulus of the constituent material. h , ℓ, t and θ geometrically characterise the microstructure, being, in turn, the length of the vertical and inclined cell walls, their thickness and inclination(Fig. 5).

In terms of the effective Young's modulus, for the equilateral triangular microstructure (Fig. 6(a))， Gibson and Ashby [40]suggested

while, for the square lattice (Fig. 6(b)),

and, if loaded in the diagonal direction,

As it can be seen from Eqs. (8) and (9), the macroscopic stiffness of the triangular and hexagonal honeycomb scales with different powers of: the former with the first power, the latter with its cube. As mentioned in Sect. 2.2, this difference is related to how the microstructure responds to macroscopic loads, that is to say with a stretch or bending-dominated behavior. As stated,the proportionality to the first power of, rather than to its cube, makes the stretch-dominated structures, typified by the triangular lattice, intrinsically stiffer and stronger than the bending-dominated ones, typified by the hexagonal microstructure.The same considerations apply in the case of the square honeycomb: stretch-dominated behavior when the load is aligned to the cell walls, Eq. (10), bending-dominated one when loaded in the diagonal direction, Eq. (11). However, because of the deformation mechanism involving "hard" modes (i.e., tension and compression), the stretch-dominated structures are characterised by post-yielding softening (Fig. 4(b)) as the initial yield is followed by plastic buckling or brittle collapse of the walls [55].Consequently, they are not the ideal candidate for energy absorbing applications that require, ideally, a stress-strain curve with a long plateau as in the case of the bending-dominated lattices (Fig. 4(a)).

It should be noted that, in deriving the relations in Eqs. (8)-(11), Gibson and Ashby [40] considered the cell walls of uniform thickness and only focused on the bending deformations of the walls. The authors, however, later on extended the analysis to include honeycombs having cell walls of double thickness, as well as the contribution of axial and shear deformations of the walls to the in-plane elastic moduli [55].

3.2 Structural analysis- and energy equivalence-based techniques to estimate the effective properties of traditional and advanced cellular materials

3.2.1 The traditional hexagonal, triangular and square lattices

By applying the principles of structural analysis similar to that described in Ref. [40], Wang and Stronge [76] obtained the equivalent constitutive equations for a two-dimensional hexagonal honeycomb composed of extensional and flexural elements. In Ref. [76] the problem is performed in the context of micropolar elasticity, theory developed by Eringen in 1967 [77].As explained in Ref. [76], a distinguishing feature of micropolar continua is the introduction of the microrotation field, an additional deformation variable independent of the translational displacements assumed in classical elasticity. Also, if considered as representative of a continuum, this model have to be carefully employed. For example, the interactions between two neighbouring material elements involve both the Cauchy stresses, as in classical mechanics, and the couple stresses, related to the microrotation gradients [79]. In addition, contrary to classical elasticity, the Cauchy tensor is not symmetric, as well as the strain tensor. Regarding the hexagonal microstructure analysed in Ref. [76], the authors described the deformation states of the representative volume element in terms of displacements and rotations of the nodes where the cell walls, represented as elastic beams, intersect. By taking into account the connectivity of the structure and enforcing the equilibrium conditions at the joints,it emerges that the relations for the normal stresses and strains obtained in Ref. [76] are in accordance with those proposed by Gibson and Ashby [40]. Conversely, assuming micropolarity and the possibility of wall stretching lead to different results in terms of the shear stresses and strains. In Ref. [76] it is also confirmed the proportionality of the effective stiffness to the third power of, ratio between the thickness and the length of the cell walls(cf. Eq. (8)).

Fig. 6. The Gibson and Ashby's model: a the triangular and b the square microstructures.

An analysis of the micropolar behavior of two-dimensional lattice geometries, the square, the triangular and the hexagonal,was also provided by Warren and Byskov [78] and by Dos Reis and Ganghoffer [80]. In both cases, the authors represented the lattice as a sequence of elastic beams undergoing extensional and flexural deformations and derived the continuum model by means of discrete homogenization [81, 82]. This method, whose basic idea is the periodic repetition of an elementary cell to define an infinite lattice, may be explained as follows. Firstly, the periodic structure is parametrised by a small parameter,,defined as the ratio between a characteristic length of the unit cell and a characteristic length of the entire structure. Then,Taylor's series expansions of the displacements and rotations are inserted into the equilibrium equations of the lattice, expressed in terms of. Finally, considering the limit situation of a continuous density of cells, corresponding to, gives the homogenized model. The effective properties, stress-strain relations and elastic constants, naturally follow from the homogenization technique. In terms of Refs. [78] and [80], it emerges that the predicted elastic moduli agree with those in Ref. [40] only in the case of slender beams. For a slenderness of 10, the discrepancy is about 5%. In accordance with [69], the study in Ref. [78] also reveals that it is necessary to retain the second-order terms in the Taylor's expansions to induce micropolar effects. If these terms are neglected, the effective material is a classical continuum whose elastic constants coincide with those presented in Ref. [40].

An alternative approach to solve the crucial passage from micro to macro and to derive the constitutive model for two-dimensional microstructures, square, triangular and hexagonal,subjected to in-plane deformations was adopted by Chen et al.[83], Kumar and McDowell [84], Bazant [85], Bazant and Christensen [86] and Perano [87]. As in Ref. [76] and [78], in the aforementioned works the discrete lattice is idealised as a sequence of Euler-Bernoulli beams while, in the macroscopic description, the discrete structure is assumed to be represented by a micropolar continuum. Few main steps summarise the suggested technique. Initially, an appropriate representative unit cell is defined. Secondly, summing the strain energies of its individual members, expressed as a function of the displacements and rotations of the extreme nodes, gives the strain energy of the discrete structure. Then, the discrete variables representing the joints' displacements and rotations are approximated by Taylor's series expansions of the corresponding continuous fields at the centroid of the unit cell [78, 86]. Substituting the Taylor's expansions into the previously obtained discrete strain energy provides its continuum approximation. Finally, equating the latter to the strain energy of the hypothesised equivalent micropolar continuum and applying the standard theory of micropolar elasticity, give the effective constitutive equations and elastic moduli. Different from Refs. [83, 87], where only the first order derivatives in the Taylor's expansions are considered, in Refs. [84-86] also the second order terms that can be integrated by parts and converted into first order ones are retained. As pointed out in Refs. [85, 86], this strategy is necessary to ensure the equilibrium of the nodes and the connectivity of the structure. Neglecting these important aspects, i.e., equilibrium conditions and connectivity of the beams, led Chen et al. [83] to the erroneous conclusion that the strain energy density of the equilateral triangular honeycomb in the continuum approximation was three times that of the hexagonal one. Indeed, the first lattice contains three times as many beams per unit volume as the second. The authors, however, went on and calculated the effective elastic constants and constitutive equations. Again, they found incorrect results in terms of couple stress-curvature relations. Specifically, the values of the couple stresses obtained in Ref. [83] are four times those provided by the vast majority of authors [78].Starting from the calculation of the strain energy of the unit cell, Davini and Ongaro [61] adopted the viewpoint of the homogenization theory [88, 89] to deduce a continuum model for a hexagonal honeycomb subjected to in-plane deformations. In their analysis, restricted to linear elasticity, the microstructure is represented as a sequence of Euler-Bernoulli beams and its continuum approximation is provided by the introduction of the linear interpolants of nodal displacements and rotations into the discrete energy of the system. In particular, in Ref. [61] the homogenized continuum, seen as the variational limit of a sequence of discrete systems of hexagonal cells with increasingly smaller size, emerges from general theorems of-convergence.At variance with [78, 83, 85-87], the limit model is a pseudo-polar continuum, that is a material that can undergo applied distributed couples without developing couple stresses. Regarding the effective elastic moduli and constitutive equations, the predicted expressions coincide with those proposed in Ref. [80] and agree with the findings of Gibson and Ashby [40] in the limit of slender beams.

3.2.2 Chiral and anti-chiral honeycombs

In the context of chiral honeycombs, Prall and Lakes [47], for the first time, investigated the mechanical behavior of a hexachiral lattice structure and derived the equivalent in-plane elastic constants, Young's modulus, shear modulus and Poisson's ratio, by employing the same method of Gibson and Ashby [40], i.e., classical theory of elasticity and Euler-Bernoulli beam elements to represent the lattice, together with a structural analysis-based technique. In addition, to formulate the problem analytically, the authors made quite ideal assumptions, as the perfect rigidity of the nodes, the absence of internal forces oriented perpendicularly to the applied load, and the linear elastic behavior of the ligaments, whose axial and shear deformations are also neglected. This leads to a Poisson's ratio of,implying an infinte value of the shear modulus and an indeterminate constitutive law. To define a more accurate constitutive model, Spadoni et al. [90, 91] revisited the theoretical account of Prall and Lakes [47] by relaxing some of their limiting assumptions, namely, the negligibility of the axial and shear deformations of the ligaments and the absence of internal forces perpendicular to the applied external load. However, similarly to Ref.[47], in Ref. [90, 91] the hexachiral lattice is analysed in the framework of classical theory of elasticity and, again, a Poisson's ratio ofis obtained. More recently, the micropolar theory of elasticity in conjunction with an energy-based technique have been successfully used to remove the indeterminacy [47, 90, 91]and to improve the characterisation of chiral lattices. Indeed, it has been demonstrated [90, 92] that investigating this special class of lattice materials in the context of classical theory of elasticity leads to erroneous results since the classical Cauchy theory can not admit chirality [92]. A remarkable contribution is due to Spadoni and Ruzzene [93] that elaborated an equivalent micropolar continuum model for a hexachiral honeycomb undergoing small displacements and rotations. Two configurations are considered. In the first, the nodes are assumed to be perfectly rigid rotating units, simplification that allows the analytical derivation of the micropolar elastic constants, while in the second the nodes are deformable, requiring a finite element model to analyse the actual behavior of the lattice. The study reveals that the examined lattice, whose auxetic behavior is confirmed in both cases, is bending-dominated and a very strong micropolar response also emerged. As a matter of fact, the derived effective elastic constants relating direct stresses to direct strains are dominated by the bending deformation of the ligaments while axial deformation on the internal components dominates the contribution of microrotations to couple stresses[93]. However, very different configurations and corresponding mechanical behavior can be obtained by varying the topology parameter β, defined as the ratio between the length of the ligaments and the distance between the center of the rings. For example, when β →0 the ligaments vanish and a hexagonal arrangement of packed rings is recovered; for β →1 the circles shrink to dots, leading to the traditional triangular lattice. As pointed out in Ref. [93], the variation of β provides the interesting opportunity to generate topologically and mechanically different lattices and dictates the transition, captured by the continuum model derived, from bending- to stretch-dominated behavior. Similar results are reported by Chen et al. [94-96] that considered the mechanical behavior of tetrachiral [94, 95] and,for the first time, anti-tetrachiral anisotropic honeycombs [96],an attractive class of chiral lattice structures having a great potential for engineering applications, as aerospace [97] or structural health monitoring components [98]. Again, the calculated closed-form analytical expressions for the homogenized elastic constants are strongly affected by the parameter. In particular,large variations in the Poisson's ratio can be achieved by changing the length of the ligaments in the horizontal and vertical directions [94]. In addition, the analysis reveals that the auxetic behavior of tetrachiral lattices is very different from that of the hexachiral ones, being the Poisson's ratio negative only at special orientations of the external load [94, 95]. Finally, the fundamental role played by the thickness of the ligaments [96] and by the radius and deformability of the rings [95] in obtaining tetrachiral and anti-tetrachiral honeycombs with minimum density and maximum stiffness also emerged. Based on the assumption of perfectly rigid rings, Li et al. [99] reported the analytical derivation of the in-plane homogenized elastic constants,Young's modulus and Poisson's ration, of an innovative tetrachiral and anti-tetrachiral hybrid metastructure, term generally used to describe lattice materials with uncommon mechanical properties [100], obtained by combining chiral and antichiral ligaments within the unit cell. As expected, the effective properties can be tuned by adjusting the topological parameters of the microstructure as the thickness and length of the ligaments and the radius of the rings. For example, according to the authors, increasing the length of the vertical ligaments leads to a remarkably increase in the Poisson's ratio while a decrease in the rings' radius provides a rapid increase in the effective stiffness since, understandably, the smaller the rings, the stiffer the lattice. Starting from the analysis in Ref. [93], Liu et al. [101] suggested a continuum theory to describe the chiral effect of two-dimensional isotropic chiral lattices and introduced a novel chirality parameter to characterise not only the conventional shear-rotation coupling but also the coupling between bulk deformation and internal rotation, fundamental feature of planar isotropic chiral structures. By applying the proposed theory to the case of a hexachiral lattice, it emerged that the effective elastic constants derived are in very good accordance with those reported in Ref. [93].

3.2.3 Honeycomb-like structures in biology

Since the physical properties of living tissues are very difficult to measure experimentally [102], cellular materials have also been a subject of intense scientific investigations in the biological field, as several natural systems have periodic designs that could easily be reproduced in terms of honeycomb-like structures. In many cases, the investigations deal with the mechanical behavior of fluid-filled plant tissues that include, as anticipated in Sect. 1, the parenchyma tissue, composed by thin-walled cells having the internal volumes filled with an incompressible fluid. As stated, the pressure exerted by the fluid, known as turgor pressure, is responsible, together with the volume of the intercellular spaces and how closely the cells are packed together, for the strength and rigidity of the cell walls [103-105]. A first attempt to describe the effects of the turgor pressure and the contribution of the cell walls' geometry on the macroscopic constants of the parenchyma is made by Nilsson et al. [106]. The authors, based on the analysis of the hydrostat, derived the Young's modulus of the whole tissue by analysing a single cell, composed by a linear elastic material, subjected to infinitesimal deformations. Despite the limiting assumptions behind, i.e., the parenchyma tissue, in reality, manifests properties that parallel those of elastic, plastic and viscoelastic solids, the proposed result highlights a fundamental aspect of the parenchyma tissue, as well as of pressurised plant tissues in general. Namely, the variable nature of the tissue's stiffness, since both the turgor pressure and the walls' properties change with age and environmental constraints [104, 107, 108]. Similarly, Georget et al. [26]evaluated the Young's modulus of the carrot tissue, modelled as a fluid-filled honeycomb, and it emerged that the provided results were in good agreement with the experimental values.Warner et al. [25], who went in this direction, focused on the deformation mechanisms of different types of fluid-filled cellular solids to characterise the elastic behavior and initial failure of food materials. According to the authors, above a critical strain,the fluid inside the cells forces the walls to stretch rather than to bend, as it happens in the case of hollow cellular solids. By taking into account the considerations in Sect. 2.2, this leads to an improvement in the mechanical resistance of the system, as the stretch-dominated structures are stiffer and stronger than the bending-dominated ones.

Another example, concerning the nature's wonders of design, involves the hygroscopic keel tissue of the ice plantDelosperma nakurense, mentioned in Sect. 1. Existing studies investigated the morphology and composition of the keel tissue, although under different assumptions, techniques and scope.Among them, Guiducci et al. [109] represented this intriguing tissue as a honeycomb-like structure with diamond-shaped cells internally pressurised by a fluid phase. Their attention was focused on describing the mechanical aspects related to the hygroscopic actuation of the ice plant but the numerical (finite element-based) and theoretical (based on the Born rule) analysis performed revealed a great improvement in the effective stiffness of the keel provided by the filler. Similar results are presented in Ref. [31], where the aforementioned concepts are generalised to pressurised honeycombs with L-shaped and Tetris tileslike cells.

3.2.4 Biological inspiration: some examples

3.2.4.1 Composite honeycombs

By shifting our attention from plant biology to plant-inspired sytems, Burlayenko and Sadowski [58] focused on the structural performance of aluminium honeycombs filled with a polyvinylchloride (PVC) foam. On the basis of the model developed, the equivalent in-plane elastic constants are derived by the strain energy homogenization technique of periodic media [58], summarised by the following two steps. In the first, three independent loading states are imposed to the unit cell, uniaxial compression in the horizontal and vertical directions, pure shear. The second consists in evaluating the corresponding strain energy density and differentiating it with respect to the volume average components of the strain, The outcome of the study suggests that the effective stiffness of the honeycomb significantly increases due to the presence of the PVC filler. These results are confirmed by Murray et al. [110] that investigated the in-plane Young's modulus of a metallic honeycomb filled with a polymeric material. In Ref. [110], in particular, the predictions are obtained through the analysis of a single cell, where the cell walls and the filler are modelled, respectively, as beam elements and plane-stress shell elements. Also, by exploring the in-plane crush response of a honeycomb with circular cells, D'Mello and Waas [111] found that filling the cells with a polydimethylsiloxane (PDMS) elastomer provided an enhancement of the energy absorption capability.

3.2.4.2 Shape-changing configurations

Finally, inspired by the shape changing characteristics of plants (cf. Sect. 1), various authors transferred the physical principles behind the reversible biological movements to create synthetic materials providing enhanced performance and novel functionalities in different fields, such as architecture [112], robotics [113, 114] or aeronautics. In the context of cellular materials, such mutable features are usually replicated by pressurising the cells of traditional honeycombs, as suggested by Vos et al.[115, 116]. Specifically, the authors developed a pressure adaptive honeycomb (PAH) by inserting air pouches into a conventional honeycomb having a hexagonal texture and, when pressurised, the pouches expand in volume and induce a change in the cells' shape and effective stiffness. Regarding the latter, Vos et al. [115, 116] demonstrated the central role played by the inner pressure in providing extra rigidity to the whole system. In addition, Khire et al. [117] evaluated the variable stiffness of a honeycomb-type inflatable structure by means of finite element simulations and it emerged that the overall rigidity primarily came from the internal pressure.

As suggested in a patent filed by Dean in 1921 [118], an alternative strategy to obtain a mutable honeycomb is based on thekirigamitechnique, a variation of the ancient Japanese art oforigami, that consists in cutting and folding a flat sheet of starting material [119-122]. From the engineering point of view, the use of kirigami has four significant features: the capability of producing a foldable/deployable structure, the provision, at the same time, of a reinforcement function and, differently from the origami, the kirigami cuts help determine the final shape, alleviating stresses that could otherwise cause the material to fracture.Finally, as described in Ref. [118], with an accurate definition of the cutting pattern it is possible to create a hexagonal honeycomb configuration since the cuts in the sheet material open up into hexagonal holes, coinciding with the honeycomb cells. Taking into account the results in Ref. [118], Neville et al. [123-125]reported how a class of kirigami honeycombs showed large shape and volume deformations, result that provides a potential platform for unusual multifunctional and shape-changing materials that could be used for morphing airframe components or space deployable structures applications. The authors, in particular, started by creating a pattern of cuts into a flat sheet of thermoplastic polymer, which was then corrugated and folded repeatedly to give a honeycomb architecture. Interestingly, the finite element simulations in Ref. [125] reveal that relatively small changes in the fold angle lead to a "Poisson's switch", that is a transition from positive to negative values of the Poisson's ratio of the resulting material. Moreover, Zhang et al. [126] and Zheng et al. [127] explored the mechanical behavior of sophisticated kirigami mesostructures obtained from multilayered two-dimensional precursors with a predefined pattern of cuts via the kirigami approach. In accordance with the abovementioned works, the theoretical and experimental studies in Refs. [126,127] prove the ability of the kirigami technique to increase the ultimate strain and to prevent the unpredictable local failures of the final material. Another example is Foldcore [128], a zigzagshaped sandwich panel core based on the Miura-ori geometry, a classic origami folding pattern whose main constituents are par-allelogram facets connected along fold lines, commonly used for folding and unfolding maps. Foldcore, differently from the conventional honeycomb cores often characterised by accumulation of humidity, complicated manufacture process and vulnerability against impact loads [129], possesses a number of intriguing properties, as open ventilation channels, superior energy absorption capability and impact strength, in-plane auxetic behavior. It is worth noting that, being not limited to any material or scale, the kirigami technique shows large potential for manufacturing on very small scales. As a matter of fact, in recent studies, to which we refer the interested reader for more references, it has been explored the folding behavior of mono- and multilayer graphene sheets [130-132], providing a starting point for the implementation of wearable, flexible and foldable electronic devices, such as smartphones, tablets, watches or microscopic robots. Notably, Blees et al. [133] built the so-calledgraphene kirigamiout of a graphene sheet, just by adding parallel cuts dividing it into an array of thin strips with short cross connections. Then, when the sheet is pulled perpendicular to the cuts, they open up and allow the sheet to stretch, while the strips buckle into a tilted wavy arrangement. If compared to the uncut graphene, the analytical investigations and experiments performed, revealed that the graphene kirigami has extremely high elongation limits (240%) and mechanical robustness.Similar results are proposed [134], where it emerges that graphene oxidepolyvinylalcohol (GO-PVA) nanocomposite sheets acquire unusual high extensibility after microscale kirigami patterning, opening up a wide range of novel technological solutions for stretchable electronics and optoelectronics devices,among other possible applications.

3.2.4.3 Hierarchical honeycombs

Taking into account the benefits offered by the complex hierarchical organization of many natural systems, in the last decade, due to the advent of additive manufacturing technologies,several attemps have been made to explore the potential advantages of adding structural hierarchy into traditional honeycombs.Among them, Haghpanah et al. [135], Fan et al. [136] and Taylor et al. [137, 138] investigated the role of hierarchy on the in-plane mechanical behavior of hierarchical honeycombs. The authors,in particular, derived numerical and theoretical models, forceor energy-based, to describe the macroscopic strength, toughness and stiffness. From these studies it emerges that hierarchy is detrimental to the specific stiffness. However, some possible ideas have been suggested to avert the aforesaid detrimental effect. One effective strategy is to iteratively replace each threeedge node of a base hexagonal network with a smaller hexagon.Pioneered by Ajdari et al. [139], this technique leads to a fractalappearing structure, often called self-similar hierarchical honeycomb, up to 3.5 times stiffer than the not-hierarchical counterpart having the same mass. Specifically, a self-similar structure exhibits statistically similar characteristics when examined both locally, at the level of individual components, and globally, at the level of the whole system. In other words, the same general characteristic is independent of the scale at which the observation is made [140]. This bio-inspired principle mimics the self-similar hierarchical design of biological systems, as muscles and tendons [141] and the intriguing collagen, whose hierarchical organisation spans from the nano- to the macro-scale [142]. Starting from the study in Ref. [139], Haghpanah et al. [143] presented a theoretical method to evaluate the in-plane stiffness and plastic collapse strength of first- and second-order self-similar hierarchical honeycombs, based on the classical plastic limit analysis [144]. With the benefits and insights afforded by the analytical machinery, the authors indicated possible ways to achieve optimised hierarchical structures of actual use, in terms of tailored combinations of stiffness and strength. For instance,how to lower the value of the stiffness while increasing the strength, in order to obtain a cellular material that is easily deformed but resistant to rupture. An extension of the concepts of classical Fracture Mechanics to cracks propagating in a self-similar regime is discussed in Ref. [145]. The analysis focuses on scaling laws defining the transition between the properties belonging to different lengths of scale and it emerges that the fracture energy is an exponential function whose exponent is only related to the considered length of scale. Finally an innovative hierarchical anti-tetrachiral structure, made of isotropic anti-tetrachiral cell walls with a negative Poisson's ratio, was examined by Wu et al. [50]. The authors, after deriving analytical expressions for the effective elastic constants of the lattice from a energy-based technique, concluded that the macroscopic properties can be significantly enhanced and manipulated by adjusting the hierarchical geometrical parameters of the microstructure that, in the case of a anti-tetrachiral lattice, coincide with the tickness and length of the ligaments and with the radius of the circles. In particular, a tunable anisotropic mechanical behavior with a Poisson's ratio having a large range of negative values can be easily obtained and this result could be very promising for the design of biomedical devices, stretchable electronics, reconfigurable soft robotics or electronic skin [50]. It should be noted that there is an enormous amount of literature focusing on the characterisation of a wide range of both biological and manmade hierarchical materials and it would be impossible to review the subject adequately. Consequently, we have only considered the contributions related to the problem touched in the present paper, i.e., estimation of the effective properties of twodimensional cellular materials, and according to the author's opinion, only the most significant works in the field have been proposed and discussed. For a comprehensive treatment and for further references to the extensive literature on the subject, one may refer to the recently published review articles [1, 15, 20, 23]and to the references therein.

3.2.5 Modelling techniques to deal with the advanced nanohoneycombs

It can be said that the above examples encompass the majority of current research in the field of mechanical modelling of two-dimensional cellular materials. However, with the development of electron microscopy technology and the recent advances in nanotechnology, an emerging class of honeycombs with features reaching down to the nano-scale need to be mentioned. For instance, inspired by the natural nanoporous silica structures in the exoskeleton of diatoms, Sen et al. [146] investigated the mechanical response, elasticity and strength, of nanohoneycomb silica structures, whose potential applications range from load-bearing to optics, catalysis, absorption or as a template for assembling novel nano-devices [146-148]. The authors,in particular, performed molecular dynamics simulations and analytical size-scaling studies to derive a theoretical model to explain the mechanisms behind the enhanced ductility and toughness observed in nano-porous silica structures [149-152]. Simil-arly to the case of traditional honeycombs, in Ref. [146] the nano-honeycomb is represented as a network of interlocking struts horizontally and vertically oriented (i.e., a rectangular texture) and, again, it emerged that the macroscopic behavior is closely related to the characteristics of the underlying architecture. The slenderness ratio of the struts, for example, strongly affects the load distribution and deformation profile since the response of the horizontal and vertical members is governed, respectively, by bending and axial deformations when the struts are slender, by pure shear and axial deformations when the struts are thick. In addition, the study in Ref. [146] reveals the existence of a critical value of the struts' thickness,Å,leading to a brittle-to-ductile transition. Specifically, for higher values of thickness the nano-honeycomb will fail by brittle crack initiation and propagation, for smaller values by plastic deformation, providing an enhanced ductility. Molecular dynamic simulations was also employed by Yang et al. [153], Biener et al.[154] and Ouyang et al. [155] to study the mechanical properties of the recently introduced gold nano-honeycombs, very promising for a wide range of engineering applications due to their high strength and low density. In accordance with Ref. [146], the predicted results, Young's moduli and yield stress, show a strong dependence on the relative density and cell walls' thickness[153].

Referring to Ref. [156] for an in-depth discussion, it should be noted that, when the material design expands toward the nanoscale, the classical theory of elasticity needs to be reviewed since an important concept has to be taken into account: the surface stress effect. Indeed, when the structures are nano-sized, due to their high surface-to-volume ratio, the surface stress effect, relying the variation of the excess free energy to the strain of the surface [156, 157], can no longer be neglected as it plays a vital role in the mechanics of nano-systems. Extensive works emphasised this aspect by showing, for example, the dramatic increase in the effective elastic constants provided by a judicious modification of the surface effect. Among them, Duan et al. [158, 159] focused on the linear elastic behavior of nano-porous cellular materials and derived the effective constants, bulk modulus, Young's modulus, Poisson's ratio and shear modulus, by means of the composite cylinder assemblage model [160] and the generalised selfconsistent method [161]. Notably, it emerged that a pore surface manipulation leads to a nano-honeycomb stiffer than its bulk counterpart, result that could enable the fabrication of sandwich structures with reduced size and weight. Also, as pointed out in Ref. [158], this is only a first step towards the improvement of nano-cellular materials since other effective physical/mechanical properties such as the thermal expansion coefficient, the electrical and magnetic conductivity or the dielectric constant, could be engineered by surface forces modifications.

Taking into account that the mechanical modelling of nanohoneycombs does not coincide with the main topic of the present paper, it should be noted that the abovementioned works, offering an overview of the current research status in the field, can be supplemented with Refs. [156, 162], where a list of references is also provided. For the interested reader, [156] can be considered a good starting point for studying the mechanics of nano-scale systems since different classical theories, e.g.Eshelby Formalism, Levin's formula and Hill's connections, are discussed and extended to the nano-scale.

4 Computational homogenization as a tool to estimate the effective properties of cellular materials

Whenever a closed-form macroscopic constitutive equation can not be derived or when it needs to be assessed, a different way to solve homogenization problems of heterogeneous materials, having a more or less periodic microstructure, is to use a computational homogenization scheme.

This method, that is probably one of the most accurate techniques in upscaling the behavior of a well-characterised microstructure [163], is based on the construction of a adequate microscale boundary value problem whose solution is used to determine the local governing behavior at the macroscale [164-169]. Specifically, according to Suquet [164], the computational homogenization scheme can be summarised by the following four steps: (i) identification of a microstructural RVE and definition of the constitutive behavior of its individual components;(ii) transition of the macroscopic input variables (e.g. the macroscopic deformation gradient tensor) to the microscale in order to formulate the microscopic boundary conditions that are then applied to the RVE (macro-to-micro transition); (iii) solution of the microscale boundary value problem and calculation of the macroscopic output variables, commonly obtained by using standard mathematical averaging equations, from the analysis of the deformed RVE, e.g. analysis of the boundary displacements and surface tractions of the RVE (micro-to-macro transition);(iv) deriving the (numerical) relation between the macroscopic input and output variables.

Among the various computational homogenization techniques developed until now, the classical first-order computational homogenization procedure is by now well established and widely used in the scientific and engineering community. This first-order approach, based on the finite element method (FEM),was first addressed for periodic microstructures at the end of 1960 [170, 171] and rapidly drawn considerable attention in the field of materials science. More recently, efforts have been made to consider more complex microstructures [172-174] and various mathematical techniques have been introduced. Authors,initially, focused on linear constituents and/or small deformations [175, 176] but, since these pioneering studies, the method has been elaborated for plastic materials [177], large deformations and arbitrary nonlinear material behavior at the fine scale.

Whereas the first-order framework has now grown towards a standard tool in computational homogenization, it is important to emphasise that this method has its strong limitations. The shortcoming, in particular, originate from the key assumption of the first-order scheme, that is the principle of separation of scales. Such principle assumes that the microscopic length scale is much smaller than the characteristic length over which the macroscopic loading varies in space [163] and, in the context of the first-order method, can be formalised as

being ℓdiscretethe size of the microstructural heterogeneities,ℓmicrothe size of the RVE considered, ℓmacrothe characteristic length of the applied load. If and only if the two conditions in Eq.(12) are met, ℓdiscrete≪ ℓmicroand ℓmicro≪ ℓmacro, the existence and uniqueness of an equivalent homogeneous medium can be proved for both periodic and not-periodic materials [178]. As a result, it is justified to assume the macroscopic uniformity of the deformation field over the microstructural representative volume element. This hypothesis, full in line with the standard theory of continuum mechanics, i.e., the principle of local action and the concept of material points, identified with an infinitesimal volume only, does not allow the application of the first-order method to the analysis of microstructural size effects affecting the macroscopic behavior or in critical regions of large gradients of deformation field at the macroscopic scale. Thus, to overcome intrinsic limitations of the first-order scheme, secondorder computational homogenization techniques have been developed [179-181].

In the second-order framework, leading to a higher-order macroscopic continuum, both the macroscopic deformation gradient and its gradient, i.e., the first and the second gradient of the displacement field, are used to determine the boundary conditions for the RVE. At the microscale, the boundary value problem remains a classical first-order one and from its solution, still obtained with a standard technique, the macroscopic stress tensor and a higher-order stress tensor are derived by enhance averaging relations based on a second-order extension of the Hill-Mandel condition (cf. Sect. 4.2). As stated, this leads to a higher-order macroscopic constitutive response and both the microscopic size effects and macroscopic localisation phenomena (i.e., high deformation gradients) can be treated in a natural way.

Referring the interested reader to Refs. [57, 178, 182] for a more detailed discussion, in the following the main concepts to numerically evaluate the effective properties of microscopically heterogeneous media are outlined. Emphasis is on the FEM-based first-order technique but the same ideas are also applicable to other types of discretization, as the finite difference method (FDM) or the finite volume method (FVM).

4.1 Computational homogenization: overview

Both the spatial arrangement and material behavior of its components strongly affect the macroscopic behavior of heterogeneous materials. Consequently, to obtain a detailed description, analyses on different length scales are inevitably required.This, however, necessitates large computational effort and, even on modern powerful computers, is practically intractable. Another complication comes from the fact that, generally, the microstructural configuration is not globally periodic. In most of the analytical homogenization strategies encountered in the literature, this difficult has been formally resolved by assuming the global periodicity of the microstructure but, for real materials,this idealised geometry may appear to be rather artificial and inappropriate. Conversely, in the computational homogenization approach the two concepts of local (i.e, the microstructure repeats itself in a small vicinity of each macroscopic point but can have a different morphology in correspondence of different material points) and global (i.e., the same microstructure is spatially repeated over the whole macroscopic medium) periodicity allow us to analyse less artificial materials having a not-uniform distribution of the microstructure, as in the case of the functionally-graded materials [174, 183] reveal that the periodicity conditions are surprisingly well suited for the analysis of materials with disordered microstructure.

In addition, due to the requirement of computational feasibility, numerical methods of homogenization usually consider a smaller sample of the heterogeneous material, the so-called RVE that, as previously mentioned, is used to determine the corresponding effective properties of the homogenized macroscopic model. According to statistically-based arguments, the RVE must contain a sufficient number of microheterogeneities, like grains,inclusions, voids or fibers, to statistically represent the whole composite and to provide the same macroscopic response as the real system [59]. This definition, however, could lead to very large RVEs when the microstructure is not-uniform. Thus, in actual computational homogenization analyses, the definition introduced by Hill [184] is usually employed: a well-defined RVE contains sufficient microstructural information and its overall response under different boundary conditions is the same. In other words, in terms of apparent and effective properties (i.e.,when the homogenized properties are determined by considering a volumesmaller than the RVE, in the first case, and when they are obtained with a volume, in the second), it can be said that the RVE is the smallest material volume for which the apparent and effective properties coincide.

Once a suitable RVE has been identified, appropriate boundary conditions are imposed to model different loading situations and to induce microscopic stresses,, and microscopic strains,, with. Through homogenization assumptions, the RVE is then regarded as a classical material element of an equivalent homogeneous medium whose effective properties are obtained by an average process [185] (Fig. 7). That is to say,the macroscopic stresses,, and the macroscopic strains,,treated as the effective stress and the effective strain fields, are calculated by averaging their local counterparts over the considered heterogeneous domain of volumeV:

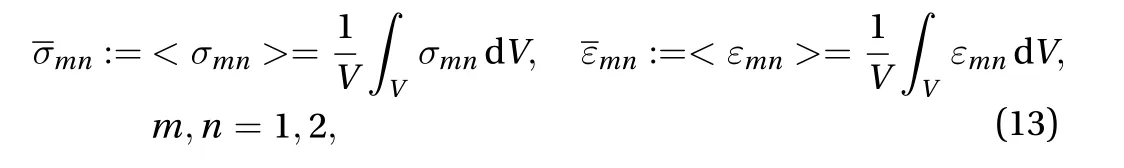
or, in terms of second-order stress and strain tensors,

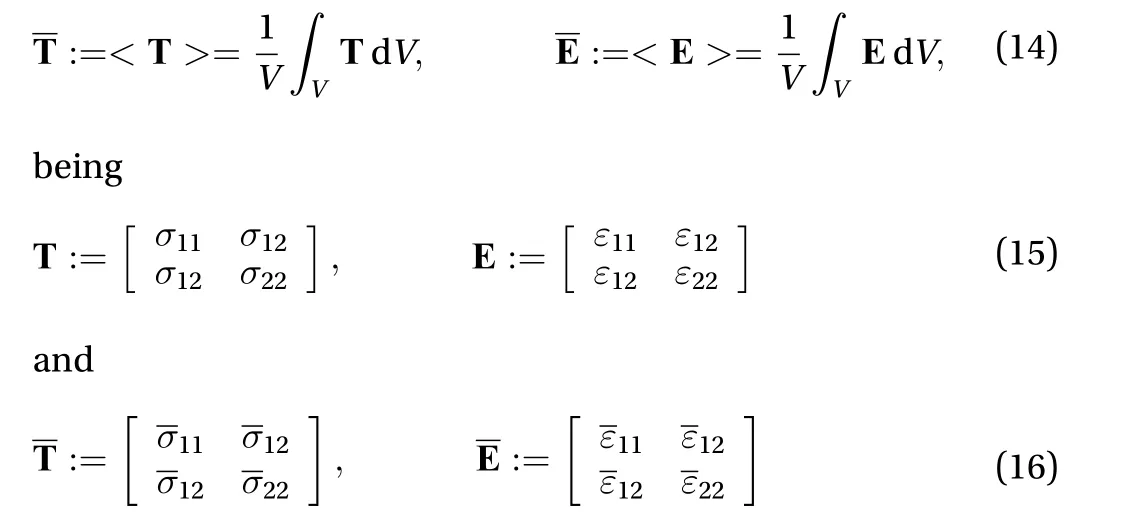
respectively, the microscopic stress and strain tensors and their homogenized counterparts. It is worth noting that, for sake of clarity, here and in the following, uppercase bold letters are used to denote a tensor quantity.

By taking into account that the statistically admissible stress field,, is such that = in V and that the kinematically compatible strain field, , is defined as the symmetric part of the gradient of the displacement field , the application of the divergence theorem to the relations in Eq. (14) provides

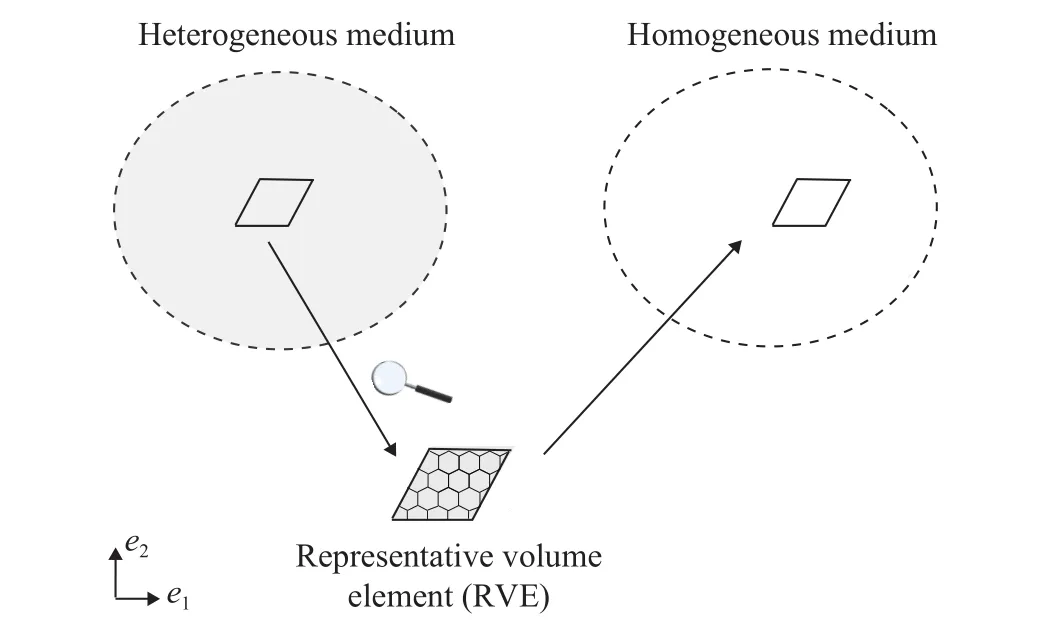
Fig. 7. The equivalent homogenous material.

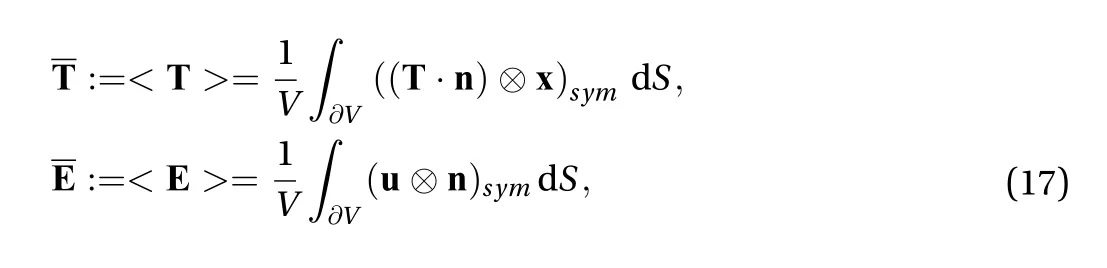
where (·)symstands for the symmetric part of the resulting tensor, ∈ ∂Vand the unit normal to ∂V.

Under the assumption of linearly elastic material behavior,the relation betweenandis expressed by the classical Hooke's law,

or, by using the Voigt notation,

with

andCmnthe components of the effective stiffness tensor, .

To highlight the effective engineering constants, Young's moduli, E1and E2, Poisson's ratios, ν12and ν21, and shear modulus, G, the constitutive law in Eq. (19) can be rewritten in terms of the homogenized compliance tensor, =-1:

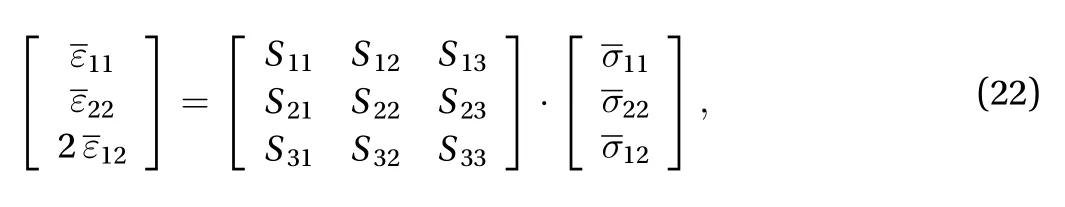
being

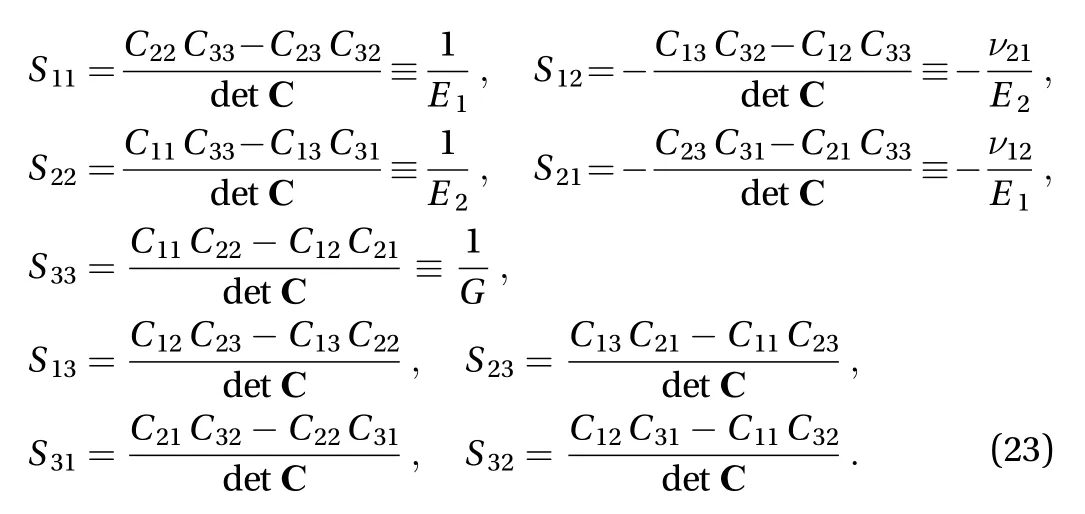
Finally, in terms of elastic strain energy density, from the averaging equations in Eqs. (14) and (17) it emerges

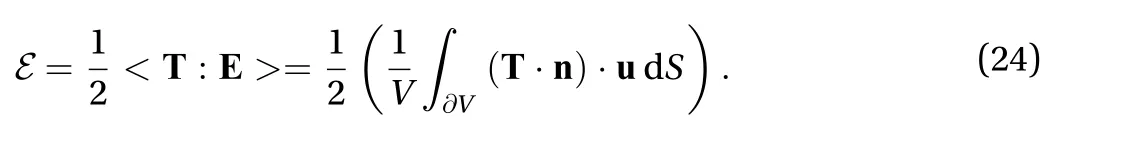
4.2 Boundary conditions

In the literature, three types of boundary conditions are usually prescribed on the RVE, kinematic uniform boundary conditions (KUBC), static uniform boundary conditions (SUBC), periodic boundary conditions (PERIODIC), so as to produce macroscopic strains,, or macroscopic stresses,, with, within a homogeneous material having the same size of the RVE.

In particular, in the KUBC case, the boundary points of the RVE,, are subjected to a homogeneous displacement,,given by

relation that leads to

with

the macroscopic strain tensor. The corresponding macroscopic stress tensor,

is then obtained by the spatial average of the local field:

In the SUBC case, the material points ∈ ∂Vare subjected to a homogeneous traction, , such that

with the unit normal to ∂ V and ~ the macroscopic stress tensor.Again, from it follows

while a spatial average of the local field gives the macroscopic strain tensor

By taking into account that heterogeneous materials can be represented as a periodical array of RVEs, PERIODIC conditions enforce periodic displacements,, and anti-periodic tractions,,on the RVE's boundary (Fig. 8):

where*is a periodic fluctuation, generally unknown,dependent on the applied global loads [60, 186]. The conditions in Eq. (33) imply that, in a heterogeneous material, each RVE has the same deformation mode and that there is no separation or overlap between the neighbouring RVEs. Generally, for a given RVE, the periodic boundary conditions, if compared to the uniform displacement and uniform traction ones, leads to a better estimation of the macroscopic properties in both the periodic and not-periodic case [183]. The convergence of the results obtained with different boundary conditions is provided by increasing the size of the RVE, as verified by a number of authors [184-188]. However, as pointed out in Ref. [56], when both the loading and the RVE's geometry exhibit sufficient symmetry, Eq. (33) can be reduced to the usual boundary conditions in Eqs. (25) or (30). Conversely, in the case of multiaxial stress states, the abovementioned symmetry considerations can not be invoked and the periodicity conditions in Eq. (33) can not be done away with.

In addition, KUBC, SUBC and PERIODIC satisfy the Hill-Mandel macrohomogeneity condition [60, 189], ensuring the micro-macro equivalence in terms of mechanical work density.In other words, the Hill-Mandel condition requires that the macroscopic volume average of the variation of work performed on the RVE is equal to the local variation of work on the macroscale and, if expressed in terms of the stress and strain quantities defined in Eq. (14), reads as

with

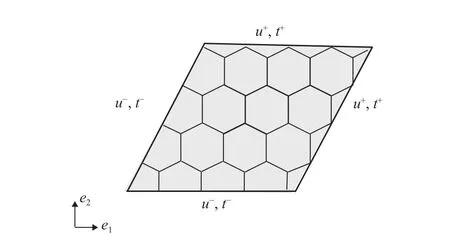
Fig. 8. Periodic boundary conditions on the RVE.

Note that, if the boundary conditions are homogeneous as in Eqs. (25), (30) and (33), Eq. (34) is valid for any material,homogeneous, heterogeneous or piecewise homogeneous. If the requirement of homogeneity is not fulfilled, the Hill-Mandel theorem does not apply, since the mean value of a product is generally not equal to the product of mean values.

4.3 Computational homogenization: an example

To offer the reader a practical example on how the computational homogenization technique can be employed to estimate the homogenized properties of a heterogeneous material, let us consider the two-dimensional honeycomb microstructure illustrated in Fig. 9.

As in can be seen, the numerical calculations involve a 75×50mm rectangular domain discretized in a number of hexagonal cells whose walls, treated as Euler-Bernoulli beams,have length ℓ and thicknessh=0.1ℓ. Finally, the Young's modulus and the Poisson's ratio of the constituent material are, respectively,Es=79 GPa and νs=0.35 (aluminum alloy [40]).

The effective elastic constants can be obtained by solving the SUBC micromechanical problem and, in particular, three load conditions are considered. The first, uniaxial compression in the1direction (Fig. 10a), and the second, uniaxial compression in the2direction (Fig. 10b), to get the Young's moduliand Poisson's ratios ν12,ν21, the third, pure shear (Fig. 10c), to gain the shear modulus G. The loading states are simulated by forces acting at the unconstrained boundary nodes of the domain, as summarised in Table 1.

Initially, from the solution of the boundary value problems corresponding to the three loading situations described, the displacements at the extreme points of the beams can be computed. In particular, if the indicesanddenote the extreme nodes of the generic e-th beam element, the followingvector completely describes the element nodal displacements:

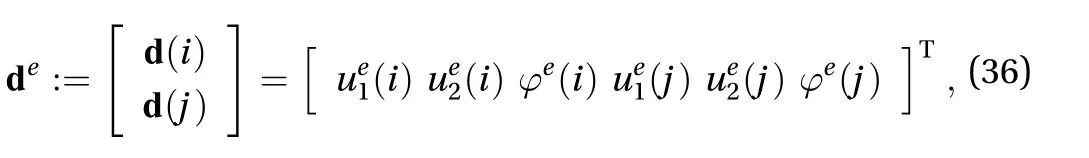
Then, the displacements and derived quantities (i.e., stress,and strain,at every point along the beams are calcu-lated by interpolation according to

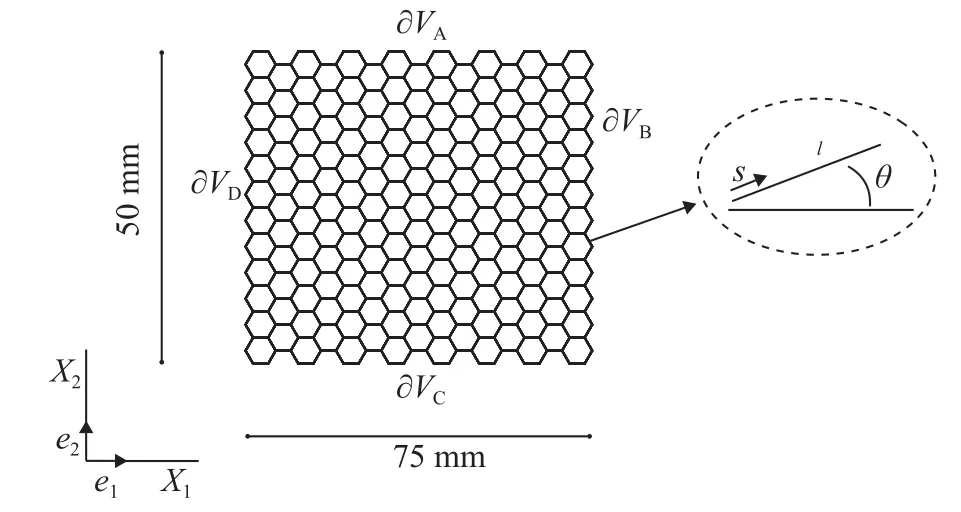
Fig. 9. Analysed domain in the numerical simulations.

Table 1 Boundary conditions used in the numerical simulations.

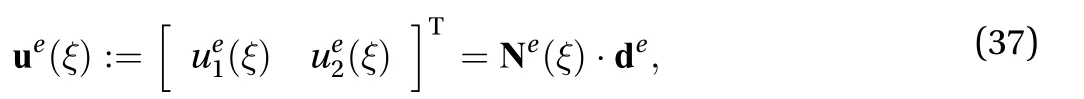
with ξ :=2x/ℓ-1 the dimensionless coordinate varying from ξ=-1at node i ( x=0) to ξ =1 at node j ( x=ℓ),

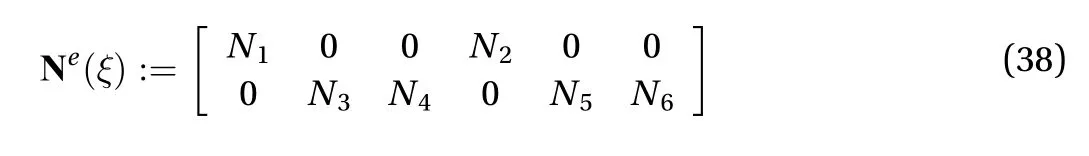
the shape function matrix whose components are given by Ref.[190]

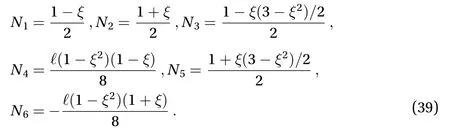
Finally, the homogenized moduli are a consequence of Eqs.(14), (22) and (23).

When the forces act horizontally, Eq. (22) leads to

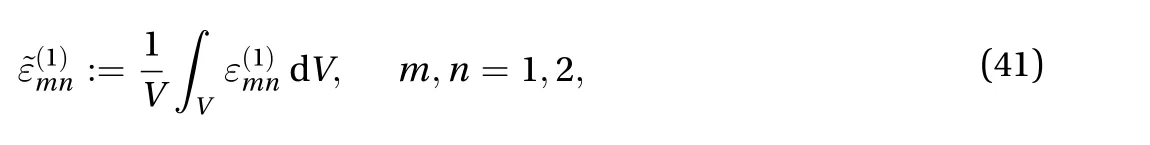
with V the volume of the examined domain. The latter, as shown in Fig. 9, is composed by a number of beams,nb, having the same length, ℓ, the same thickness,h, and widthb. Accordingly,

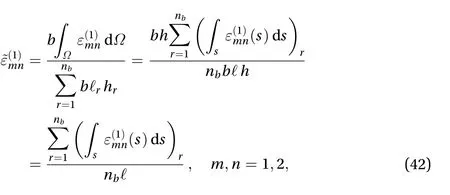
where Ω is the area of the domain,s=(cosϑr,sinϑr) a parametric coordinate such that 0 ≤s≤ ℓ (Fig. 9), ℓr, hr, ϑr,respectively, the length, the thickness and the inclination of the-th beam.

Also, if

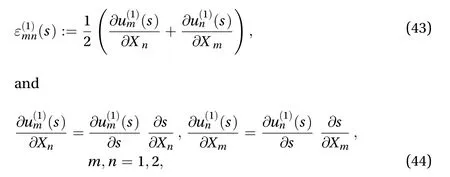
are substituted into Eq. (42), it follows

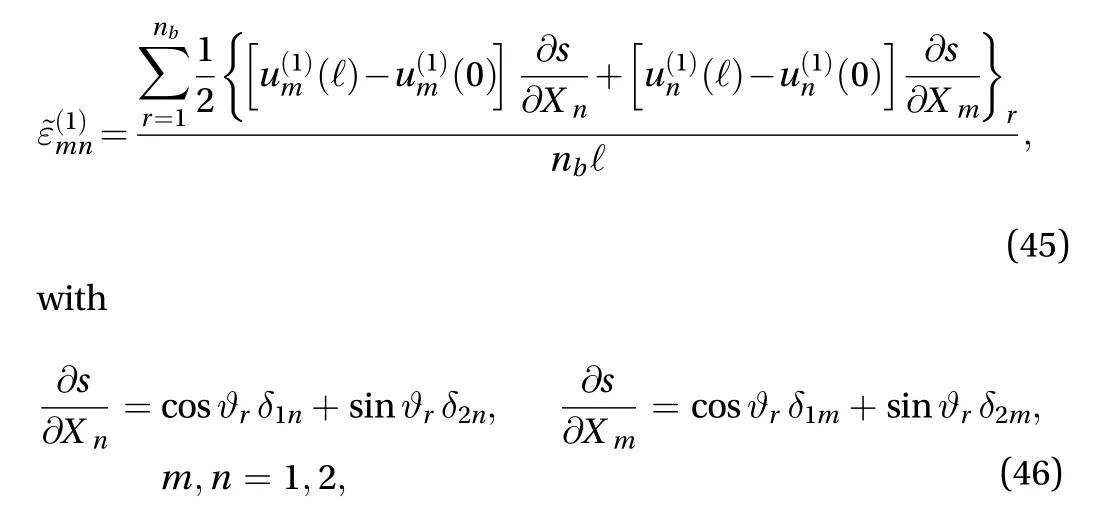
δmnthe Kroneker delta,(s) andthe displacements of the points along the beams due to the application of. Finally,Eqs. (23) and (40) lead to

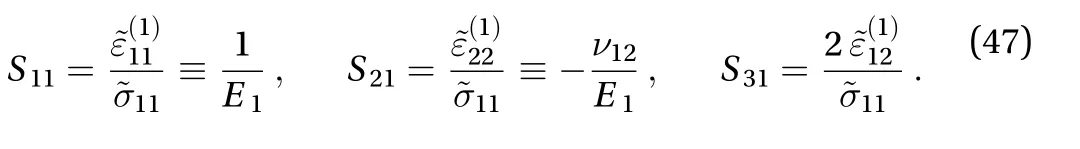
With analogous calculations, forces acting vertically provide

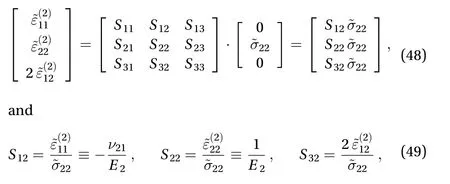
while, in the case of pure shear,

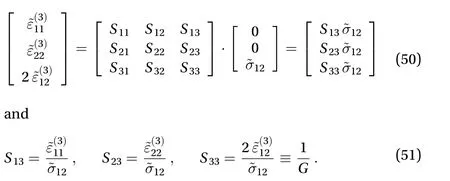
The outcome of the analysis is presented in Table 2, in terms of elastic constants, and in Table 3, in terms ofconstants.Firstly, a convergence study is conducted to determine the number of elements required to produce converged material properties. This is achieved by starting with a small number of elements (cells) and continuously refining the mesh, i.e.,discretizing the domain in an increasing number of cells having gradually smaller length, until no variation in the results is observed. It is found that acells discretization is enough to get converged numerical results and to correctly capture the essential properties of the honeycomb. Tables 2 and 3 also illustrate the comparison between the numerical solutions obtained and the theoretical findings of Gibson and Ashby (cf. Sect. 3.1)that, as stated, are currently the principal reference in the field of cellular materials. As it can be seen, generally emerges a verygood agreement between the analytical and numerical predictions, being the discrepancy between the two estimates of averagely 1 % in the case of the elastic moduli, Table 1, and of averagely 1.5% in the case of theconstants.

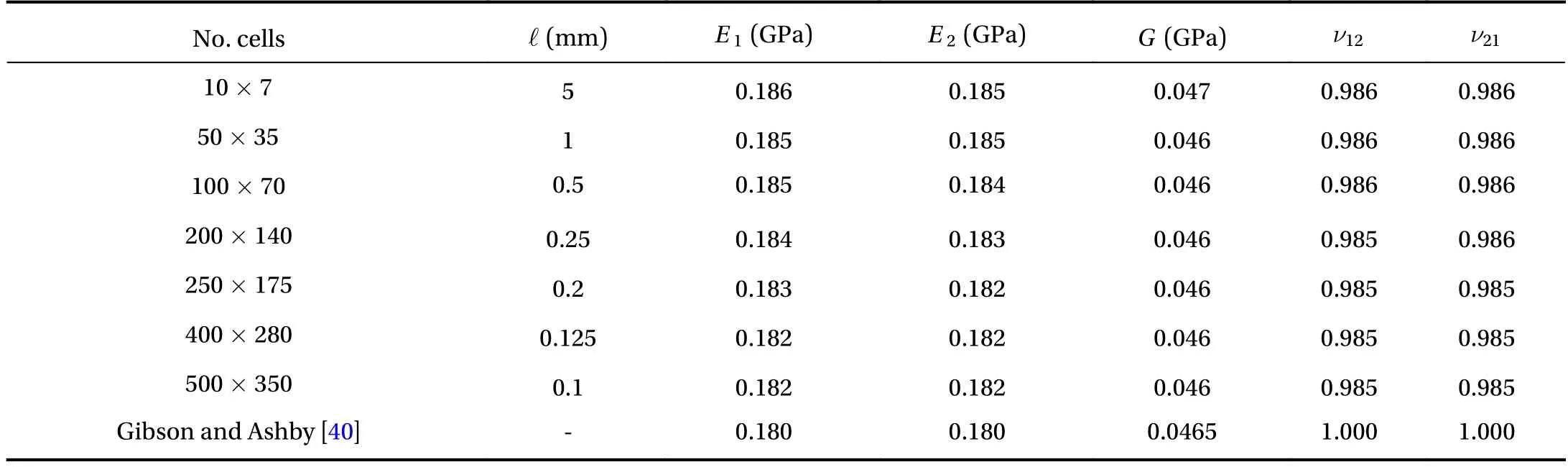
Table 2 Computational homogenization, an example: elastic moduli.

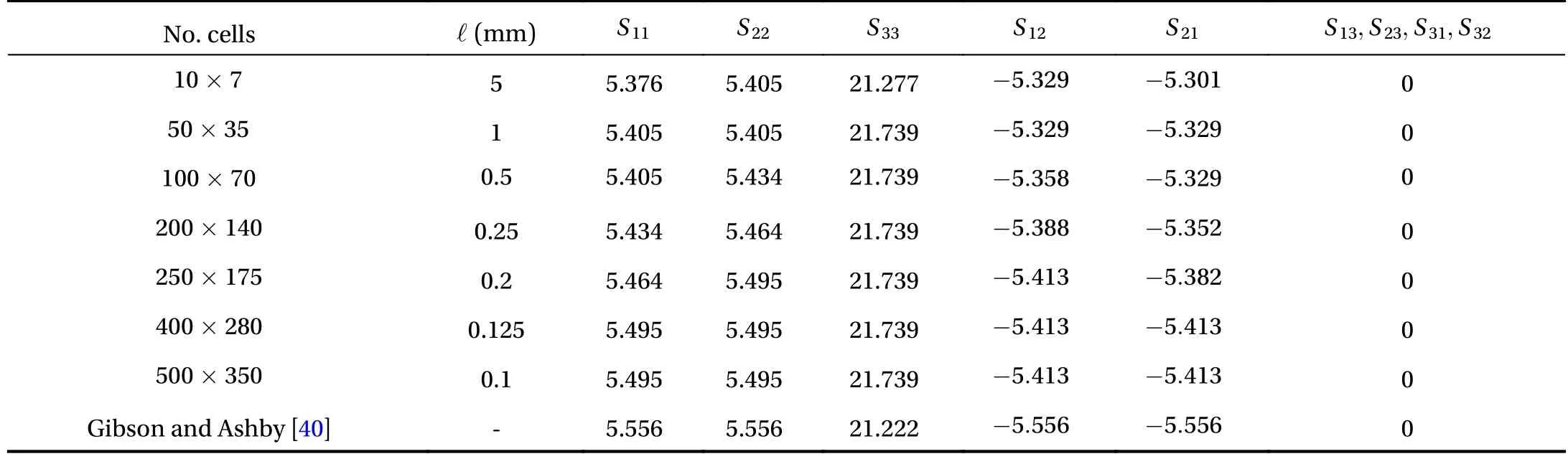
Table 3 Computational homogenization, an example: S mn constants (GPa- 1).

5 Conclusions

The cellular nature of many biological materials, providing them with low density, high strength and high toughness, have fascinated many researchers in the field of botany and structural biology since at least one century. Bamboo, sponges, trabecular bone, tooth and honeybee combs are only few examples of natural materials with cellular architecture.

It has been widely recognised that the geometric and mechanical characteristics of the microscopic building blocks play a fundamental role on the behavior observed at the macroscale.

Up to date, many efforts have been devoted to the analysis of cellular materials to predict the structure-property relations that link the macroscopic properties to the mechanics of their underlying microstructure and a great variety of analytical and numerical techniques can be found in the literature.

In this paper, the most significant contributions are critically presented and an extended list of references is also provided.