Piezoelectric energy harvesting from flexible delta wings

Jml S. Alrowijeh, Muhmmd R. Hjj*

a Graduate Assistant, Engineering Mechanics Program, Virginia Tech, Blacksburg, Virginia 24061, USA

b J. Byron Maupin Professor of Engineering, Engineering Mechanics Program, Virginia Tech, Blacksburg, Virginia 24061, USA

Keywords:Energy harvesting Delta wing Piezoelectric Bending stiffness Mass ratio

ABSTRACT The potential for harvesting energy from a flexible delta wing using a piezoelectric bimorph is experimentally investigated. Different configurations of the proposed harvesting system were tested in a wind tunnel over a broad range of airspeeds. In addition to evaluating the level of harvested power, an analysis is performed to extract critical aspects for the relation between speed,flexibility, geometry and the potential power that can be harvested from a clamped, cantilevered flexible delta wing at low angles of attack and low speeds. This analysis provides an insight into parameters that impact energy harvesting from flexible membranes or elements.

Harvesting energy from airflow using piezoelectric transduction has several advantages over the use of micro-turbines at small scales. First, reducing the size to fit the harvester within a small space will not result in significant reduction in the efficiency as observed in the case of micro turbines [1]. Second,piezoelectric energy harvesters do not include many components that could potentially break as in the case of micro-turbines.Finally, their weight is smaller than that of a microturbine, which includes different components in addition to the turbine. As such, they would not add significantly to the weight of a sensing or computing device.

Different aeroelastic phenomena have been exploited to harvest energy from rigid body motions of wing sections or beams undergoing flutter [2-8] and of cylinders undergoing vortex-induced vibrations [9, 10], galloping [11-16] or vibrations of other bluff bodies [17]. Other studies considered flow energy harvesters with piezoelectric material that has fractional order current-voltage characteristics [18]. Fewer studies have considered energy harvesting from flexible motions of structures induced by fluid flows. Zakaria et al. [19] harvested energy from sustained oscillations of a flexible beam when placed in an air flow at preset angles of attack. The setup had the advantage of eliminating the need to attach a rigid structure to the beam. Orrego et al. [20]performed an experimental study on energy harvesting from the flutter of a flexible piezoelectric membrane placed in an inverted flag configuration. The study evaluated the influence of geometrical parameters of the flag on the flapping behavior and the resulting energy output.

In spite of advances made, there remain some challenges when it comes to piezoelectric energy harvesting from aeroelastic vibrations. The most important of these challenges are the range of airspeeds over which energy can be harvested, level of harvested power and power density defined in relation to the mass or volume of the harvester. Towards improving these metrics, we investigate experimentally and detail critical aspects for the relation between speed, flexibility, geometry and the potential power that can be harvested from a clamped, cantilevered flexible delta wing at low angles of attack and low speeds. The delta wing is shaped in the form of the Greek uppercase letter delta () with the top vertex of the triangle facing the incident flow. As shown in Fig. 1, the base of the triangle is attached through an arm to a piezoelectric ceramic transducer (PZT) bimorph. When placed at a non-zero angle of attack, the incident airflow coming in contact with the leading edges, defined along the two sides of this vertex, rolls up around these edges to form leading-edge vortices on both sides, causing a reduction in the pressure above the wing and increasing the lift force. Depending on the flexibility of the wing, it may deform under the resulting aerodynamic forces. This deformation causes the aerodynamic loads to change, which causes the wing to deform again.

Fig. 1. Picture of the fabricated delta wing energy harvester main parts. The wing has an arm that is attached to one end of a bimorph.The other end of the bimorph is attached to servo motor that allows for changing the angle of attack with respect to the incident flow.

The structural geometric nonlinearities, associated with large deformations of the flexible wing, and aerodynamic nonlinearities caused by flow separation and vortex roll-up result in sustained limit cycle oscillations (LCO). Tang and Dowell [21]demonstrated experimentally that the structure aerodynamic interaction could take place at low airspeeds. Attar et al. [22]showed that, for a specific speed, the amplitude of the LCO increases as the angle of attack is increased. In both studies, the considered angles of attack were small (less than 5). Yet, when drawing energy from these vibrations through piezoelectric transduction, the whole system may behave differently because the overall damping, frequency of oscillations, and level of power extracted are affected by the electric load.

The present experimental results provide insight into the range of delta wing parameters that affect the level of energy that can be harvested from a clamped, cantilevered delta wing in low speed flows. Particularly, we investigate the effects of varying the geometry of the delta wing, the angle of attack and speed on the level of harvested power. We also present non-dimensional relations between the level of harvested power, mass ratio and rigidity of the delta wing as a guide to explain physical aspects of flexible harvesters such as the one presented here and improve their performance.

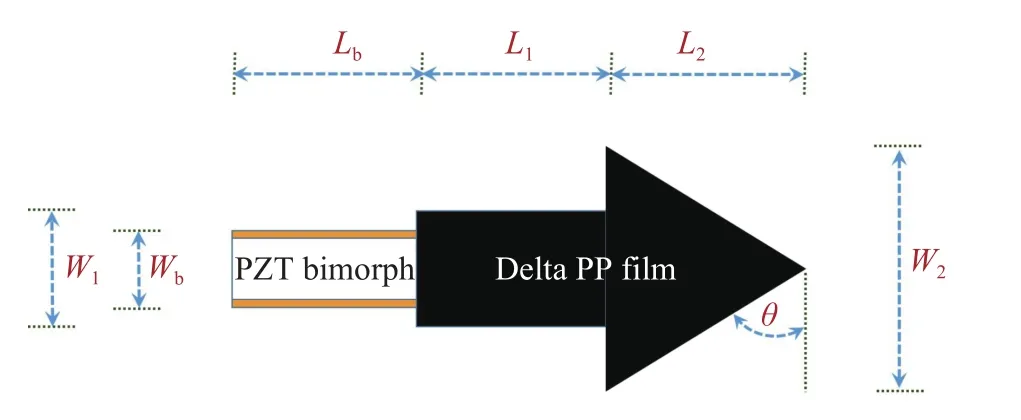
Fig. 2. Schematic of the delta wing-bimorph harvester.

A schematic of the tested wings is shown in Fig. 2. The wing with a root chord, a wing spanand leading edge sweep anglewas made out of flexible polypropylene PP plastic film that is 0.2 mm thick. This material was chosen due to its high resistance to fatigue, cracking, stress and low cost [23]. We note that for a constant root chord, changing the wing span,, is effectively changing the sweep angle. The wing had an arm of lengthand widththat was attached to a bimorph. The bimorph is 27 mm long, 10 mm wide and 0.5 mm thick. The other end of the bimorph was attached to a servo motor mechanism as shown in Fig. 1. This motor is used to rotate the wing and place it at any desired angle of attack,, with respect to the incident flow. Designations and dimensions of the tested configurations are presented in Table 1. As will be shown below, these configurations yield important information regarding the effects of varying the wing's area or mass and the rigidity of the material in relation to the flutter speed and harvested power.

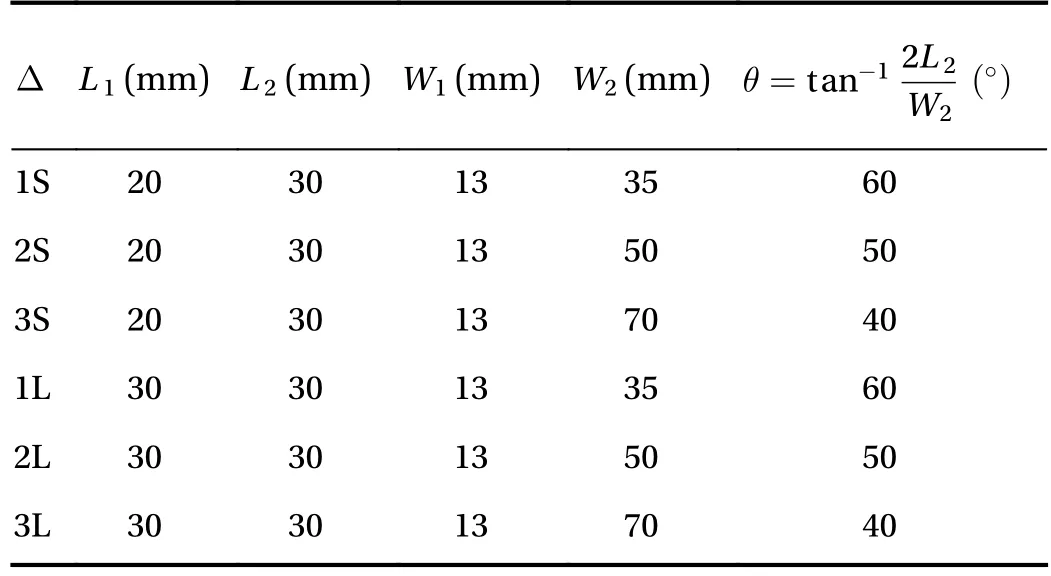
Table 1 Designations and dimensions of the tested Delta wing harvester.

Figure 3 shows an example of the variations of the measured voltage and power with the load resistance. The voltage plot shows that it increases to a maximum value that is maintained constant as the load resistance is increased beyond 1 MΩ. The power data shows that the optimal electric load for harvesting energy is 200 kΩ. Measurements for different configurations showed no change in the optimal load resistance for energy harvesting. As such, this resistance value was used in all subsequent measurements.

The responses of the different configurations at different flow speeds differed significantly as the fluttering delta wing exhibited different states even for the same configurations. Examples of these states are shown in Fig. 4. In one state, the response is periodic with one frequency as shown from the time series of Fig. 4(a). In another state, the response had a larger amplitude at smaller frequency with significant higher frequency variations during each half cycle as shown in the time series of Fig. 4(b).

Fig. 3. Variations of the measured voltage and calculated power from the measurements with the load resistance.

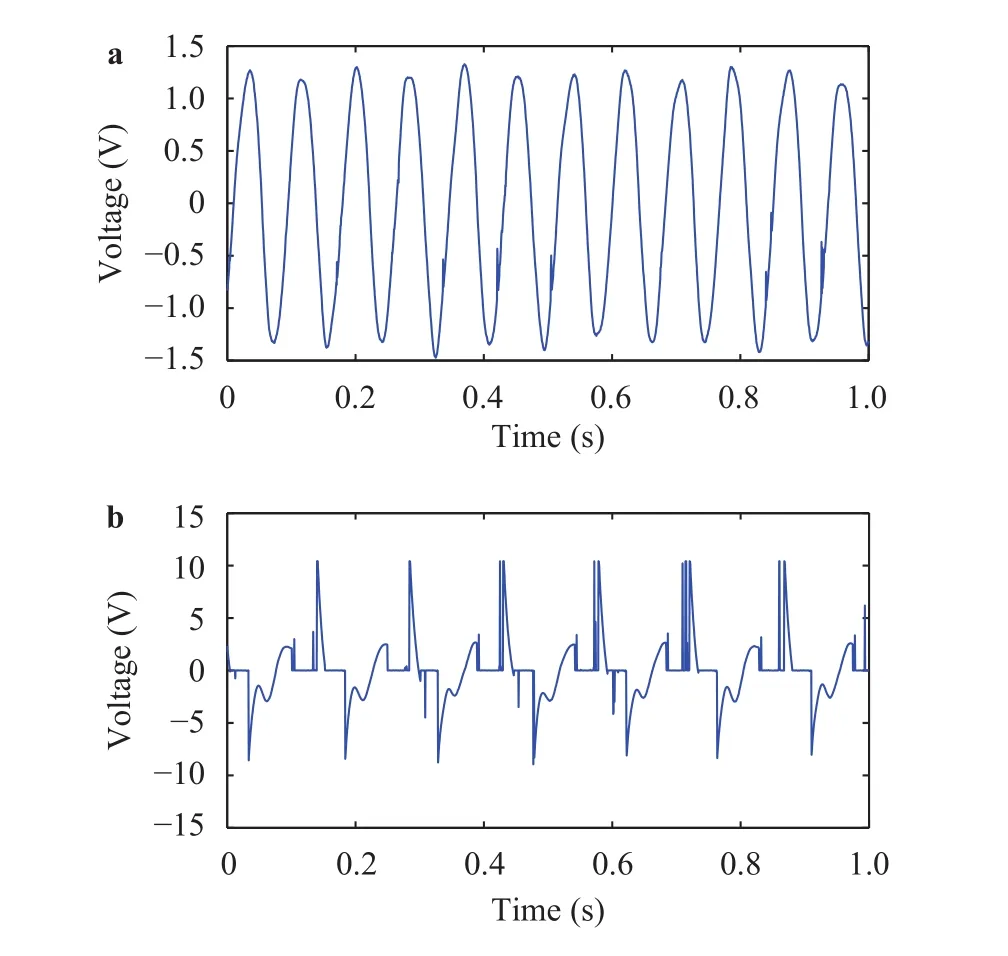
Fig. 4. Two states of response determined from the voltage time series at flow speed of 7 m/s at 5.2 angle of attack. flow speed of 9.5 m/s at 6.2° angle of attack.

All configurations were tested at angles of attack that varied between 1°and 6.5. This range was determined by the fact that flutter was observed over this range. To determine the effects of varying the angle of attack on the harvested power, we plot in Fig. 5 the harvested power as a function of the angle of attack for different flow speeds for configuration 2S. The plot shows that the peak power at any incident speed, except for 9.5 m/s is obtained when the angle of attack is near 3.4. In contrast, the dependence of the harvested power on the speed is more significant. Other tested configurations yielded similar behavior indicating that although flutter requires a non-zero angle of attack,the dependency of the harvested peak power on the angle of attack over the range between 1and 6.5is weak relative to its dependency on the incident airspeed.

Using measurements from tests performed at different angles of attack for different flow speeds, we plot in Fig. 6 the variation of the harvested peak power for each of the above harvester configurations with the incident air speed. The plots show that the length of the arm holding the delta wing, defined by, affects the onset of the flutter speed with the longer arm resulting in a lower onset flutter speed. The onset of the flutter speeds for configurations 1L and 1S, are respectively 5.5 m/s and 7 m/s. The corresponding numbers for 2L and 2S are respectively 4.5 m/s and 6.5 m/s and for 3L and 3S 4 m/s and 5 m/s respectively. In contrast, the S configurations, which designate shorter arm lengths result in higher levels of harvested energy.

Fig. 5. Power variation with the angle of attack at different flow speeds - Configuration 2S.

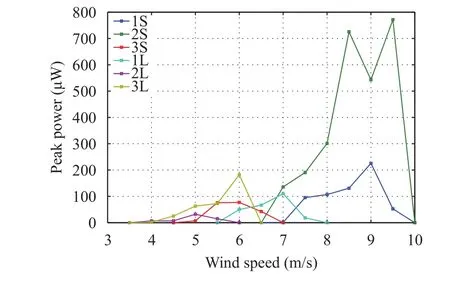
Fig. 6. Variation of peak power with the incident airspeed.

To understand the above seeming contradiction between the ability to harvest power at lower speeds when the arm length is longer and more power when the arm length is shorter, we note that the level of harvested voltage,, is related to the exerted moment and force at the tip of the bimorph by the fluttering delta wing. This action is dependent on the polypropylene material density,, and its thickness, and flexural rigiditydefined by:

where E is the Young's modolus and v is the Poisson's ratio of the polypropylene material. The harvested power is also dependent on the wing's geometry defined here by the wing's spanW2, given that its root chord length is maintained constant,on the air density ρf, on the incident flow speedU, and on the electric field strength of the bimorph Eb. As such, we define the non dimensional mass ratio μ, and bending stiffness β [24-27]

as two dimensionless parameters that impact the performance of the delta wing harvester defined by its harvested dimensionless voltage and given by

Figure 7(a) and 7(b) show the variation of the non dimensional harvested voltageversus the bending stiffnessrespectively for forandconfigurations. The mass ratios,=4.50, 3.15, and 2.25 correspond respectively to configurations 1, 2 and 3. The results show that configurations 3L and 3S, corresponding to the lowest mass ratio yield almost the same level of harvested energy when the bending stiffness varies over a range between 0.1 and 0.2. These two configurations do not harvest energy outside this range. As the wing span is increased, resulting in a slightly larger mass ratio,=3.15, there is a pronounced difference between the L and S configurations. Although the 2L configuration requires a higher non-dimensional bending stiffness to harvest energy at the same air speed, the 2S configuration will yield a higher level of harvested power over almost the same range of bending stiffness between 0.1 and 0.2 as configuration 1. However, this takes place at larger airspeeds.The plots also show that wings with higher mass ratio will harvest energy at a higher speed and require a higher non-dimensional bending stiffness to harvest energy. These results show that there is a critical balance between the mass ratio and bending stiffness for optimal energy harvesting from flexible delta wings.

Fig. 7. Energy harvesting regimes defined by the non-dimensional power as a function of the non-dimensional stiffness β for different mass ratios for the S and L configurations.

Among the considered geometries and for this specific delta wing material, the best harvester in terms of generating the largest peak power is the one referred to as configuration 2S at flow speeds equal to or higher than 7 m/s. It has a sweep angle of 50, root chord of 30 mm and a wingspan of 50 mm. The maximum harvested output power was 771.3 μW, which corresponds to a peak power density of which about 2.2 mW/cm3at a flow speed of 9.5 m/s.

Different configurations of a flexible delta wing energy harvester were tested. The results showed that the arm length between the base of the wing and the bimorph can be adjusted to harvest energy over a specific range of airspeed. Additionally,the bending stiffness and mass ratio of the wing, that cover both material properties and geometric parameters of the wing, can be adjusted to increase the level of harvested power depending on the available wind speed.

Acknowledgments

M.R. Hajj acknowledges the support of the Center for Energy Harvesting Materials and Systems and the National Science Foundation of United States under Grant 1035042.