基于连续损伤力学的轮盘超转破裂行为预测与验证

2018-09-18胡绪腾宋迎东

航空发动机 2018年4期

孙力，胡绪腾，宋迎东，2

（南京航空航天大学能源与动力学院1，机械结构力学及控制国家重点实验室2：南京210016）

0 引言

在工程中设计承担载荷的结构与构件必须进行静强度校核。以航空发动机转子为例，轮盘的破裂大多是非包容的，会引起灾难性后果[1]，因此必须对轮盘的破裂转速进行静强度校核。传统设计方法通常是对结构在最大正常工作载荷下的应力或结构能够承受的极限载荷进行计算或估算，通过与材料许用应力对比，确定其安全系数，最后根据设计准则对静强度储备安全系数的要求评判结构设计是否满足静强度要求。工程上常采用平均应力法[2]、小变形解析法[3]、大变形解析法[4]等方法预计轮盘的破裂转速。这些方法多基于工程经验或简单轮盘结构，误差较大。而进一步发展出的基于非线性有限元分析的局部应力应变法，根据轮盘体内最大应力[5]或最大塑性应变[6]来确定轮盘的破裂转速，但其无法对轮盘破裂形式进行有效预测和分析。随着对材料塑性变形和断裂行为研究的深入，通过对其进行合理建模，进而通过非线性有限元分析对轮盘的超转破裂形式进行预测成为可能，有利于对轮盘结构进行更合理地设计和优化。

对于金属材料塑性变形行为的研究已较为成熟，而在金属材料的断裂行为与建模研究方面，经过不断研究与发展，提出2类延性断裂模型：（1）以宏观变量（如最大拉应力、静水压力、等效应力等）描述材料断裂特性的宏观连续介质模型，如：Johson-Cook模型[7]、Wilkins模型[8]；（2）描述微观孔洞生长聚合的微观力学模型，如：McClintock 模型[9]、Gurson 模型[10]、Rice-Tracey模型[11]。其中Johson-Cook等模型在工程上得到广泛应用。Wierzbicki等[12-15]经过一系列研究，提出的基于等效塑性应变、应力3轴度以及Lode角参数的扩展的Mohr-Coulomb模型，也取得了良好的预测结果。但这些模型大多是非耦合的，即模型中的损伤参数不影响材料本构模型，使其描述的断裂行为在应力应变曲线上表现为断裂处应力突然下降，对材料失稳后的表现描述得过于简单[16]。

为发展和完善发动机轮盘的超转破裂分析技术，本文针对直接时效GH4169高温合金，研究和评估耦合的连续损伤模型对其拉伸变形和断裂行为的描述和预测能力，并检验了模型对模拟盘超转破裂行为的预测能力。

1 连续损伤力学模型

连续损伤力学首先由Kachanov[17]在研究蠕变时提出，又由Rabotnov[18]与Lemaitre[19]等对其进一步发展。连续损伤力学认为，在某一确定状态的材料中，损伤缺陷处于均匀弥散分布状态，而此状态下材料表现出的性能是由材料自身性能与细微损伤耦合作用的结果，并使用宏观变量对此状态下的材料性能进行描述。含有损伤的材料弹性响应表现为

式中：C0为无损伤下的材料刚度；D为材料当前损伤变量。

不同的损伤变量D的确定方法，构成一系列连续损伤模型。采用1种基于等效塑性应变的耦合的连续损伤模型，其最简单的损伤变量可用如下线性方程描述

式中：εp为等效塑性应变；εf为断裂塑性应变。相应损伤变量增量为

用线性方程描述材料损伤显然过于简单，因此引入损伤指数m，得到一系列满足上述特征的损伤变量与损伤变量增量

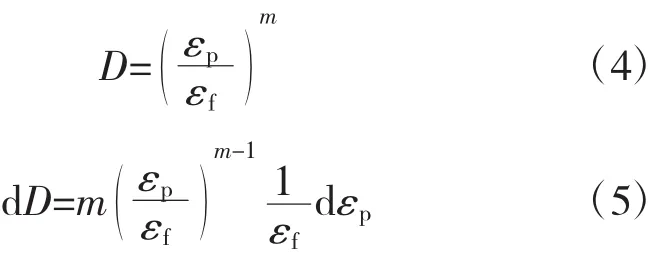
连续损伤力学模型中认为孔洞等损伤处于弥散分布状态，定义材料性能损失Ds。一般认为材料损伤变量与材料性能损失数值相等，即Ds=D，但文献[16]指出Ds≤D。故引入软化指数β，令Ds=Dβ。定义软化系数 ω（D）为

得到屈服方程

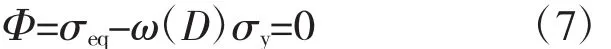
对于复杂的损伤速率与软化速率，损伤变量D和软化系数ω（D）可进一步推广为

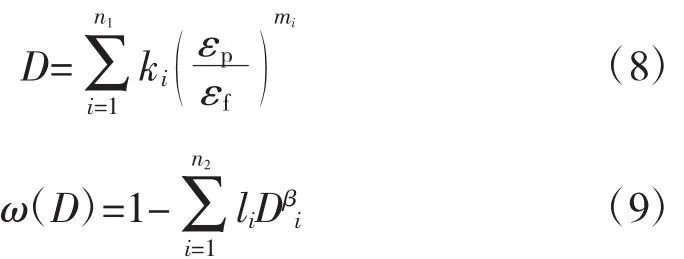
其中

2 直接时效GH4169合金连续损伤力学模型的建立

采用上述连续损伤力学模型对直接时效GH4169合金的拉伸变形和断裂行为进行建模，确定其塑性本构模型参数和损伤模型参数。本构模型参数由光滑圆棒试样拉伸试验结果拟合获得，损伤模型参数通过光滑圆棒试样拉伸响应的有限元分析确定。

2.1 塑性本构模型

由光滑试样拉伸试验得到的直接时效GH4169合金的工程应力-应变曲线和真应力-真应变曲线如图1所示。其中真应力-真应变曲线由工程应力-应变曲线直接转化得到。为建立完整描述其塑性变形响应的本构模型，假设材料在颈缩失稳前损伤较小，以失稳前的真应力-真应变曲线来建立其塑性本构模型。根据其塑性变形曲线的特点，采用如下非线性硬化模型（式（10））来描述其塑性硬化行为，硬化模型参数拟合结果见表1。

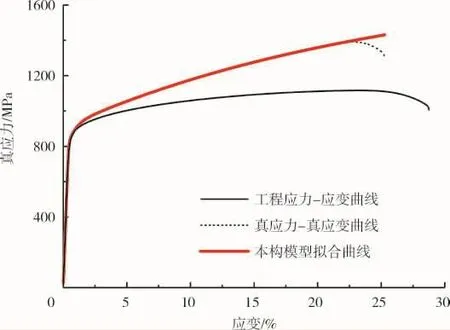
图1 直接时效GH4169拉伸应力-应变曲线与本构模型计算曲线

表1 直接时效GH4169塑性本构模型参数

从图1中可见，本构模型可以准确地描述在试样颈缩失稳之前的真应力-真应变曲线。

2.2 损伤模型

为描述直接时效GH4169合金的拉伸断裂行为，采用如下形式的软化系数，其中β=1。

由于在建立本构模型时假设颈缩失稳前损伤较小，即大量损伤集中在失稳后发生，忽略了失稳前损伤，在软化系数加入后对本构模型进行修正得到屈服方程

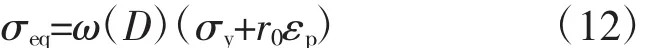
为确定直接时效GH4169合金的损伤模型参数，编制了上述本构模型与损伤模型的ANSYS用户材料子程序，通过对光滑圆棒试样的拉伸响应进行有限元计算和对比分析确定其损伤模型参数，结果见表2。光滑圆棒试样拉伸试验结果与无损伤模型有限元计算结果（即纯弹塑性有限元计算结果）和连续损伤模型有限元计算结果的对比如图2所示。从图中可见，建立的直接时效GH4169合金的连续损伤模型比纯弹塑性本构模型能够更好地预测光滑圆棒试样的拉伸响应。

表2 直接时效GH4169合金损伤模型参数

图2 光滑圆棒拉伸响应曲线与有限元计算结果

3 基于连续损伤模型的直接时效GH4169合金缺口拉伸响应预测

基于上述建立的连续损伤模型，对缺口半径R分别为0.5、2和5 mm的3种直接时效GH4169合金缺口圆棒试样的拉伸响应进行预测分析，验证连续损伤模型预测直接时效GH4169合金拉伸断裂行为的可行性。缺口试样的几何尺寸如图3所示。3种缺口试样的有限元模型如图4所示。

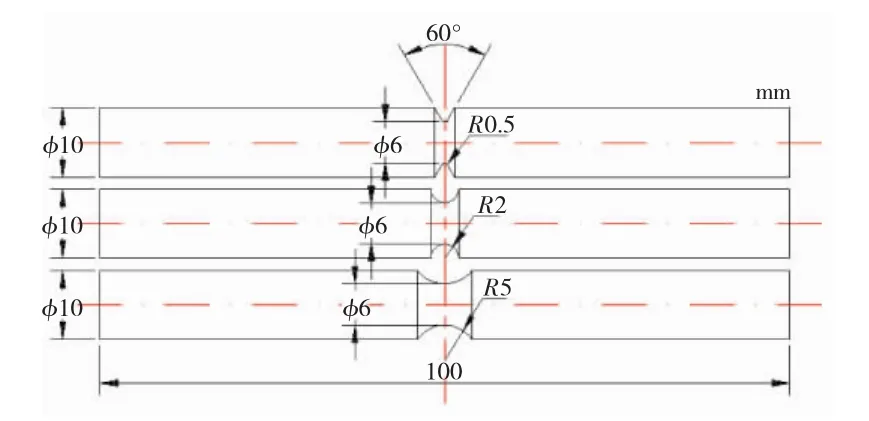
图3 3种缺口试样的尺寸

图4 3种缺口试样的有限元模型

R=0.5、2和5 mm试样试验数据与无损伤模型及连续损伤模型有限元计算结果的对比分别如图5～7所示。从图5中可见，对于R=0.5 mm尖锐缺口试样，无损伤模型计算的极限强度高于试验结果（试验结果具有一定分散性），且到达载荷极限时的轴向变形计算结果远大于试验结果。对于R=2、5 mm的缺口试样，虽然极限强度与达到极限载荷时的轴向变形误差不大，但是无损伤模型无法准确地预测缺口试样拉伸响应的下降段与断裂的时刻。

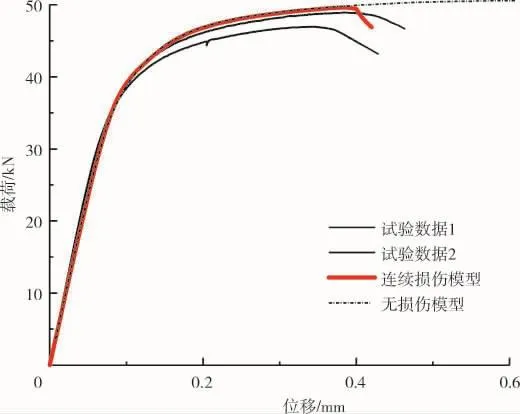
图5 R=0.5 mm缺口试样拉伸响应试验与有限元计算结果

图6 R=2 mm缺口试样拉伸响应试验与有限元计算结果

图7 R=5 mm缺口试样拉伸响应试验与有限元计算结果

综上可知，连续损伤模型不仅能够更准确地计算其光滑圆棒试样的拉伸响应，而且可以较准确地预测3种缺口试样的拉伸响应。对3种缺口试样，连续损伤模型不仅可以较准确地预测缺口试样的极限拉伸载荷，而且可以较合理地预测试样发生断裂的时刻（即发生断裂时的变形量）。

4 基于连续损伤模型的GH4169合金模拟盘破裂转速预测

基于上述建立的连续损伤模型，针对直接时效GH4169合金模拟盘超转破裂行为进行预测，验证连续损伤模型预测轮盘破裂转速与破裂模式的可行性。模拟盘实物和有限元模型分别如图8、9所示。

图8 模拟盘实物

图9 模拟盘有限元模型

采用弧长法非线性有限元求解方法对模拟盘的盘缘径向变形随转速的变化曲线进行计算，得到的模拟盘转速-径向位移曲线如图10所示。从图中可见，该模拟盘的破裂转速计算结果为37714 r/min。计算终点时模拟盘的等效应力与等效塑性应变分别如图11、12所示。从图11中可见，模拟盘辐板与轮毂过渡区域集中出现等效应力大幅缩减（可认为已缩减为0）。而从图12中可见，模拟盘辐板与轮毂过渡区域的等效塑性应变显著增大。根据连续损伤力学模型，材料在此处发生了最大量的损伤，并达到了断裂阈值，可认为模拟盘在辐板根部处发生沿圆周方向的开裂（即径向破裂）。

图10 模拟盘转速-径向伸长曲线

图11 计算终点等效应力

图12 计算终点等效塑性应变

为验证上述结果，对模拟盘开展了超转破裂试验，模拟盘在试验器中的安装状态如图13所示。模拟盘超转试验测得的破裂转速为35898 r/min。模拟盘破裂转速有限元计算结果与试验结果的误差为5.059%。试验过程中拍摄记录的模拟盘超转破裂过程如图14所示。从图中可见，模拟盘首先在辐板根部区域产生沿周向的裂纹，裂纹沿周向撕裂一定程度后

图13 模拟盘试验安装状态

图14 模拟盘超转破裂照片整体发生破坏，这与基于连续损伤模型预测的轮盘超转破裂模式是一致的。