某低压涡轮盘破裂转速分析与试验验证

邵 帅，刘秀芝，魏 峰，邱 丰

（中国航发沈阳发动机研究所，沈阳110015）

0 引言

轮盘作为航空发动机的关重件，必须确保轮盘在可能出现的超转范围内工作而不破裂。对于双转子发动机，由于低压涡轮轴较细，考虑到加力燃烧室对其的影响，低压涡轮盘发生超转的概率较高。因此，低压涡轮盘最需要受到破裂转速的限制，并优先考虑低压涡轮盘的破裂试验[1]。目前，国内外破裂转速的预测方法主要有理论计算方法和基于有限元的多种计算方法，包括平均应力法、最大应力法、局部应变法及残余变形法等[2-8]。目前，工程上常用的破裂转速计算方法是平均应力法[9]，文献[10-12]对破裂转速预测方法进行了试验验证。本文为实际工程问题，结合有限元计算结果，采用平均应力法和局部塑性应变法对涡轮盘进行破裂转速分析，对轮盘破坏起始部位进行预测，并与试验和失效分析结果进行对比分析。

1 轮盘破裂转速预测

1.1 平均应力法

轮盘的破裂模式主要有子午面破裂和圆柱面破裂。子午面破裂是在轮盘子午面以周向应力为主的情况下发生的；圆柱面破裂则是在轮盘某半径高度上以径向应力为主的情况下发生的。平均应力法是从轮盘平均承载角度分析轮盘子午面和圆柱面失效的破裂转速预测方法。采用加权平均周向应力法，基于轮盘2维轴对称有限元计算结果求解平均周向应力公式[3]为

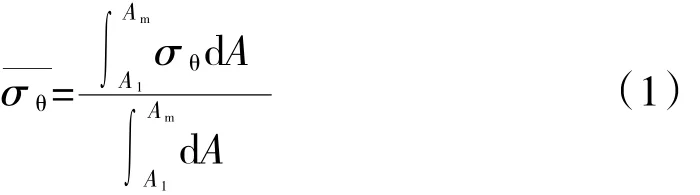
基于轮盘2维轴对称有限元计算结果，针对平均径向应力最高截面，根据径向应力沿截面线积分的方法可求得最大平均径向应力。

基于有限元计算结果，采用平均应力法计算破裂转速储备公式[4]为

式中：kb为轮盘破裂转速储备；σb为材料的强度极限；σ为轮盘最大稳态转速下的平均周向应力；k为材料利用系数。

低压涡轮盘材料选用高温合金GH4169[13]，破裂试验环境为常温，有限元分析时考虑了叶片的作用和离心载荷。采用PLANE183单元建立2维轴对称有限元模型进行弹性应力分析[5]，定义槽底以上的轮缘凸块部位为具有一定厚度的平面应力单元。

通过对轮盘子午面和圆柱面进行破裂转速储备分析可知，轮盘子午面破裂转速储备较低，轮盘的主要破坏模式为子午面破坏。考虑材质的分散性，根据可靠性要求，选取轮盘随炉试件拉伸性能的最低值、最高值和平均值进行破裂转速分析，假定材料利用系数为1.0，基于平均应力法预估轮盘破裂转速，见表1。

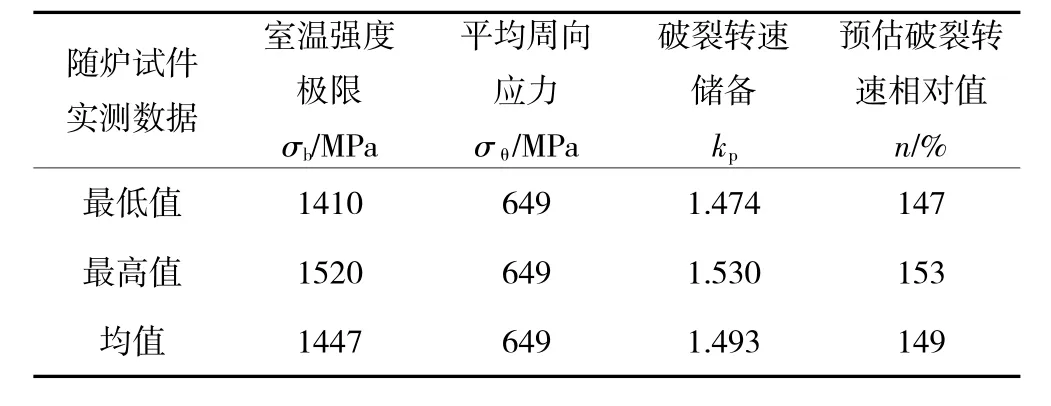
表1 破裂转速分析

1.2 局部塑性应变法

对轮盘进行局部应力应变分析，采用的应力-应变曲线根据随炉试件实测力学性能数据的平均值获得，将材料手册[6]数据绘制的应力-应变曲线与随炉试件实测力学性能数据平均值绘制的应力-应变曲线进行对比，如图1所示。

图1 应力-应变曲线

建立局部塑性应变分析3维有限元模型，计算相对转速154%时轮盘局部塑性应变分布，如图2所示。从图中可见，局部塑性应变较大部位位于榫槽槽底，且该部位应变以周向应变为主，各转速下槽底局部塑性应变分析结果见表2，塑性应变-转速关系如图3所示。从塑性应变变化规律可见，当转速由157%上升至158%时，榫槽槽底局部塑性应变大幅度提高，按照局部塑性应变法预测在该转速范围内轮盘可能发生破裂，起裂位置为榫槽槽底。

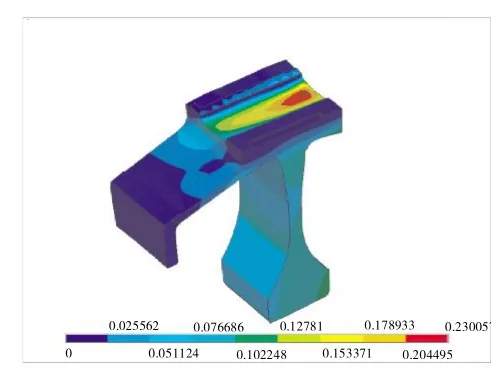
图2 局部塑性应变分布

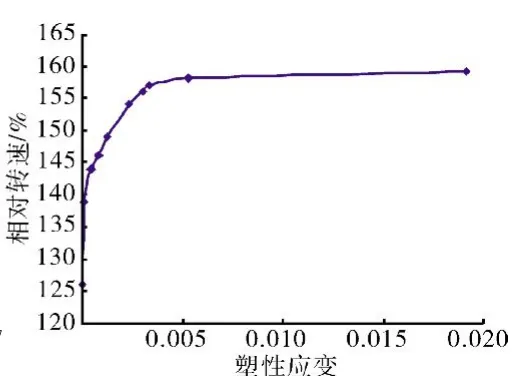
图3 槽底塑性应变-转速曲线

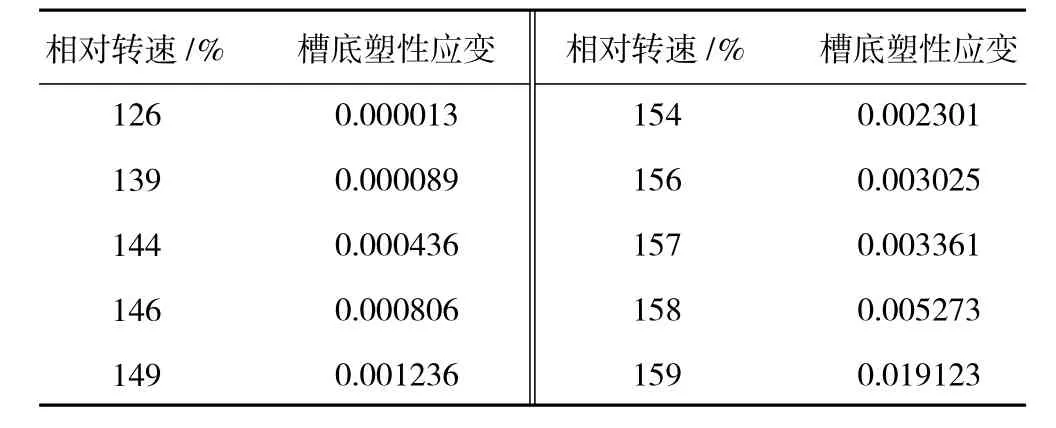
表2 塑性应变随转速变化趋势

2 试验结果与分析

2.1 应变计算结果与测量结果对比

为了验证轮盘局部塑性应变法分析模型的正确性，在轮盘榫槽附近布置应变片测量周向应变，由于局部应变最大部位位于槽底，该部位不便于粘贴应变片，将应变片布置在轮盘前端面靠近槽底的位置，如图4所示。各转速下应变计算结果、测量结果及相对误差见表3，计算结果与各测点实测应变值绘制曲线如图5所示。从图中可见，应变计算结果与测量结果较为吻合。

2.2 高速摄像记录

在试验过程中，采用高速摄像记录轮盘的整个试验历程。当试验转速上升至154%时，轮盘发生子午面破裂。按时间顺序选取具有代表性的高速摄像照片如图6所示，整个试验过程如下：

图4 榫槽附近应变测点位置

图5 榫槽附近应变测点位置

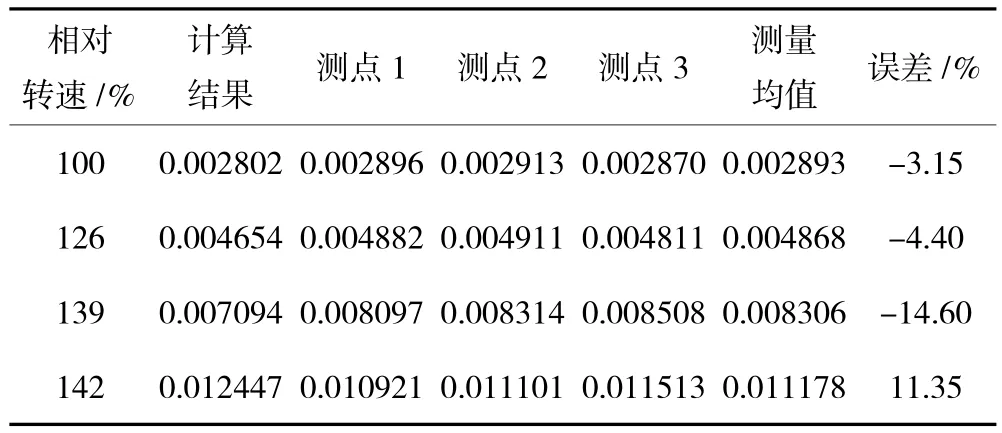
表3 应变计算结果与测量结果对比

图6 高速摄像记录

（1）第 1排 5幅照片记录了试验转速升至154%时试验件运行过程。转速升至154%前，试验件运行状态正常，目视整个轮盘的塑性变形不明显。当试验转速升至154%后，轮盘子午面发生破裂；

（2）第2排5幅照片记录了轮盘子午面首断截面破裂的过程。轮盘开始发生破裂后，轮盘变形明显，按逆时针旋向90°位置轮盘发生第2次破裂，轮盘第1个部分彻底断开；

（3）第3排5幅照片记录了轮盘第2个部分破裂的过程。轮盘第1个部分发生破裂后，轮盘变形进一步变大。从第2次破裂位置起，按逆时针旋向90°位置轮盘发生第3次破裂，轮盘第2个部分彻底断开；

（4）第4排4幅照片记录了轮盘发生破裂后的过程。整个轮盘破裂之后，破裂的轮盘撞击到防护层，产生明显的火花。

2.3 计算与试验结果对比

轮盘在相对转速达到154%时发生子午面破裂，破裂后整体形貌如图7所示，首断截面形貌如图8所示。将实测破裂转速与预测破裂转速进行对比，结果见表4。

从对比结果可见，在常温条件下，当材料利用系数取1.0时，采用平均应力法预测破裂转速仍然低于实测破裂转速，采用实测力学性能最高值预测破裂转速与实测值最为接近，误差为-0.65%，采用实测力学性能平均值预测破裂转速误差为-3.25%，由于实测破裂转速高于预测破裂转速，本文数据不能给出材料利用系数；采用局部塑性应变法预测破裂转速高于实测值，采用实测力学性能平均值预测破裂转速误差为1.95%～2.60%；本文采用2种方法预测低压涡轮盘（常温条件下）破裂转速与实测破裂转速较为接近，局部塑性应变法预测精度相对更高。

图7 轮盘破裂后整体形貌

图8 首断截面形貌

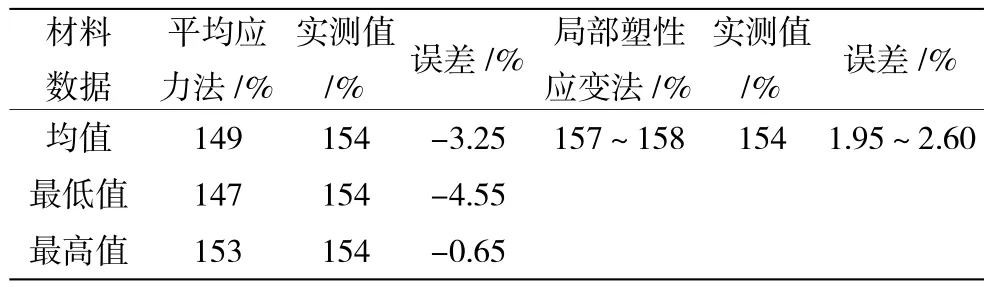
表4 破裂转速实测与预测对比

3 失效分析[14-15]

轮盘首断截面端口分为盘缘侧断口和盘心侧断口，断口宏观图像如图9所示。断口靠近盘缘榫槽槽底及辐板中心区域为纤维区，安装边及辐板两侧区域为剪切唇区，断口表面可见放射线形貌，放射线由槽底向辐板方向扩展。盘心侧断口纤维区形貌主要为等轴韧窝形貌，剪切唇区形貌为剪切韧窝，表明该断口为瞬断断口。

图9 断口宏观图像

根据剪切唇区的剪切韧窝方向判断，断裂由盘缘侧向盘心侧扩展，扩展方向如图10中红色箭头所示。因此，随着转速提高至轮盘破裂转速，低压涡轮盘发生瞬断破坏，由榫槽槽底部位起裂，后扩展至盘心。该分析结果与第1.2节预测轮盘破坏起始位置一致。

图10 裂纹扩展方向

4 结论

本文采用平均应力法和局部塑性应变法进行破裂转速预测，并与试验结果和失效分析结果进行对比分析，得出结论如下：

（1）采用平均应力法和局部塑性应变法进行破裂转速预测的结果与试验结果吻合较好；

（2）采用局部塑性应变法预测轮盘破裂起始部位与失效分析结果吻合较好；

（3）对于本文研究的轮盘及其工作环境，平均应力法预测破裂转速低于实测值，局部塑性应变法预测破裂转速高于实测值，且局部塑性应变法预测精度相对更高。