航空发动机空气管路应力优化设计

2018-09-18陈志英郑家祥李建福

航空发动机 2018年4期

陈志英，郑家祥，李建福

（北京航空航天大学能源与动力工程学院，北京100191）

0 引言

空气管路系统是航空发动机的重要组成部分，其可靠与否关系到发动机的安全性。由于发动机空气管路系统的刚性强、空间走向复杂，而且随着温度变化与机匣存在热变形不协调，易在局部位置产生较大的应力应变，导致该系统发生低周疲劳断裂等故障。针对航空发动机空气管路应力问题，国外主要遵循ASME压力容器规范以及 SAE ARP699[1]、SAE AS1960[2]、SAE AS1985[3]等专门针对空气导管的设计标准。国内航空领域较早开始研究自动敷管和调频技术[4-5]；随着行业发展，应力引起的低周疲劳断裂及泄漏问题在飞机管路系统设计中引起重视，并形成以弯管和添加补偿器为主要手段的应力补偿方法[6-8]；随着数字仿真技术的成熟以及计算软件的发展，优化设计技术作为解决复杂产品设计问题的最佳技术途径，已成为航空发动机管路调频以及其他部件设计的研究热点[9-10]。而目前国内对航空发动机空气管路低周载荷应力研究较少，基于应力问题的管路优化设计更少，发展发动机空气管路应力问题设计方法，具有重要的工程应用价值。

本文基于弹塑性分析法，研究应力应变与载荷因素、结构参数的关系；并利用按结构分解的系统优化设计技术，以降低应力为目标，对管路部件和管线进行优化设计。

1 载荷分析与优化方法

1.1 载荷分析与应力校核

航空发动机空气管路主要承受内压、热载荷、位移载荷等。承受压力是空气管路完成任务的根本需要，而其余载荷由管路工作环境带来，属于附加载荷。

（1）压力载荷。管路中一次应力主要由压力产生。空气管路管壁厚度与截面圆内径之比一般小于0.1，属于薄壁承压容器，直管段各向应力与壁厚成反比，与管径成正比；而在管路弯管、三通等局部部位，挤压角半径、弯管半径、主支管夹角等参数对管路承压能力影响较大[11-12]。

（2）附加载荷。热载荷、外部位移约束是空气管路附加载荷的主要内容，而附加载荷在管路中主要产生二次应力。空气管路系统从启动前到工作状态，管内压力和温度均会使管路发生变形。管路入口位移与机匣变形协调，出口需满足任务系统提供的位移约束，与支架、阻尼器等结构的装配关系会提供局部端点位移约束，这些位移约束构成空气管路的位移载荷。由于热膨胀变形与位移约束在应力求解时同属位移边界条件，可以得到

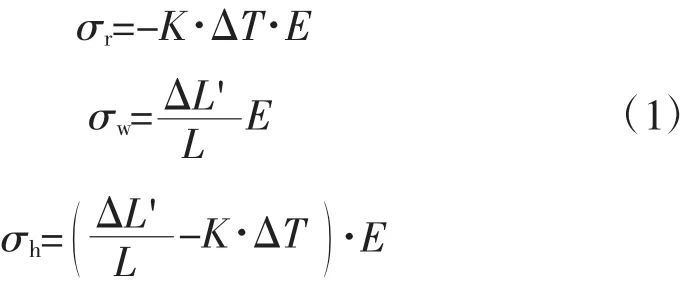
式中：σr为热应力；σw为位移载荷产生的附加应力；σh为热-位移载荷附加应力；ΔL'为位移边界条件引起的变形；K为热膨胀系数；L为结构尺寸；ΔT为温度变化值。

（3）应力校核准则。管路应力校核方法有2种：应力分类校核法和综合应力校核法。

分类校核法指在静力承载时，一次应力比二次应力更危险，应该重点校核，二次应力不会导致结构破坏；而反复加载时，二次应力对结构寿命的影响不能忽略。

综合应力校核法不受限于一次、二次应力的分类方式，将各种类型载荷引起的应力综合，以合应力校核管路强度。管路低周疲劳破坏采用综合应力法校核管路应力时，相关标准与研究[13-15]建议采用畸变能密度理论，即米塞斯应力屈服准则

本文参考管路应力校核的思路，以米塞斯应力为考核应力做结构特性分析和优化，而不具体作应力校核。

1.2 优化方法

航空发动机管路系统优化流程如图1所示。管路特性分析目的是获得管路中压力场、温度场、应力场，找出初始设计薄弱点。在结构分解阶段，先将对结构特性影响大的零部件单独分解出来分析优化，然后再作管路管线优化。需单独优化的零部件包括三通、支架局部结构、接头等，在管路系统整体优化之前，先对这类零部件进行结构优化，目的是先优化与应力集中强相关的局部结构参数，在之后管线优化过程中这类参数直接作为常量参与计算，以降低优化问题变量维数，提高计算效率，并降低计算难度。

图1 航空发动机管路系统优化流程

2 管路系统弹塑性分析

环控引气管路系统是发动机空气管路系统的重要组成部分，而9级引气管路系统的工作压力和温度最高，管线较复杂，模型如图2所示，其应力问题具有代表性。9级引气管路系统入口连接高压压气机第9级后机匣，出口接环控引气阀门，整个系统主要由3根管段、4个支架、5个接头组成，管段材料为GH536合金，工作时热膨胀变形受多个位移边界条件限制，其所受载荷见表1。

图2 环控引气管路系统模型

表1 环控引气管路系统主要载荷条件

先对整个管路系统作流动与热分析，再用压力场、温度场分析结果作为边界条件，对管路系统作结构特性分析。由于载荷较大，初步仿真计算发现，三通肩部、腹部和支架耳片根部应力较大，三通最大应力超过材料屈服极限。参考JB 4732[13]与ASMEⅧ-2[14]中压力容器塑性分析极限载荷确定标准，采用小变形弹-塑性分析法[16]，材料应变-应力关系参考材料手册[17]，对引气管路系统进行应力应变分析，计算结果如图3所示。

图3中弹塑性分析结果表明，管路局部已经严重屈服，塑性变形较大，三通的应力应变最大，是结构设计最薄弱位置。

图3 管路系统弹塑性分析载荷同步加载结果

飞行任务和阀门布置位置会影响空气管路载荷加载过程，而载荷加载过程对结构弹塑性分析结果会产生影响[18]。不同加载过程与变形曲线如图4所示，应力与应变结果见表2。

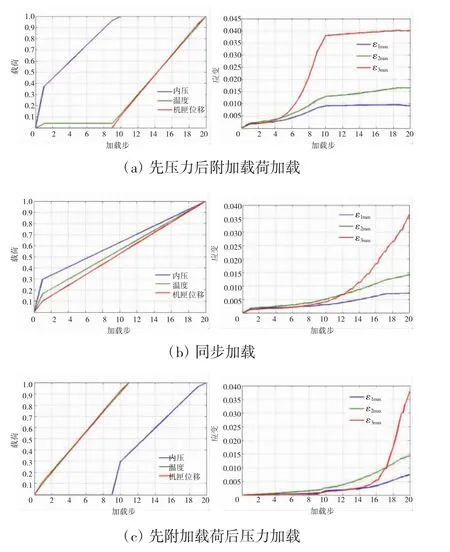
图4 载荷与应变曲线

表2 加载过程与应力应变结果

图 4 中载荷采用归一化，σ1max、σ2max、σ3max分别为 3个三通位置最大应力，ε1max、ε2max、ε3max分别为最大应变。不同加载过程的变形曲线均表明，当管路内压接近1.6 MPa（归一化载荷0.6）时，应变开始急剧增大，三通位置承压能力不足；变形曲线斜率显示压力载荷对管路塑性应变影响大，而附加载荷影响相对小。引气控制阀门分别布置在出口或入口位置时，管路实际载荷加载过程近似于图 4（a）、（c），而表 2 显示不同加载过程对管路最大应力值和其出现的位置都会造成影响，应力计算结果差值最大达到4.64%。在不考虑成本、结构质量等因素时，将阀门布置在入口，对降低管路应力更有利。根据安全性设计原则，其后的计算按先压力后附加载荷方式加载。

3 三通优化计算

按管路系统优化流程，先对三通进行优化设计，提高部件承载能力。航空发动机空气管路系统通常采用2种三通结构，如图5所示。

图5 三通结构

先建立参数化模型，选择与交贯线局部曲率相关的结构尺寸作为变量。然后做结构分析，管路温度为570℃，内壁压力为2.7 MPa，支管入口端轴向约束；由于2种结构均属于异径三通，出口端需施加气动平衡力。随机抽样生成210个样本点，其中200个样本用于拟合标准二次响应面，10个样本用于检验拟合精度；以最小化最大应力为目标，选用筛选算法，分别对2个结构进行优化。结果表明，响应面拟合精度分别为0.8%和0.4%，优化结果见表3。在各参数中，σamax、σbmax、分别对 L1、θ敏感度最高，响应面曲线关系如图6所示。

表3结果显示，通过优化2种三通结构最大应力均减小，结构a和b的最大应力分别降低3.07%和2.03%，且结构b的最大应力小于结构a的。图6（a）表明结构a应力降低主要是通过减小支管半径L1实现的，优化后的支管半径为取值域下界，与结构b的相似，表明从三通承压能力出发，结构b具有优势。图6（b）θ-σbmax响应面函数关系表明三通应力随θ绝对值增加而增大，正交三通承压能力强。

表3 三通优化结果

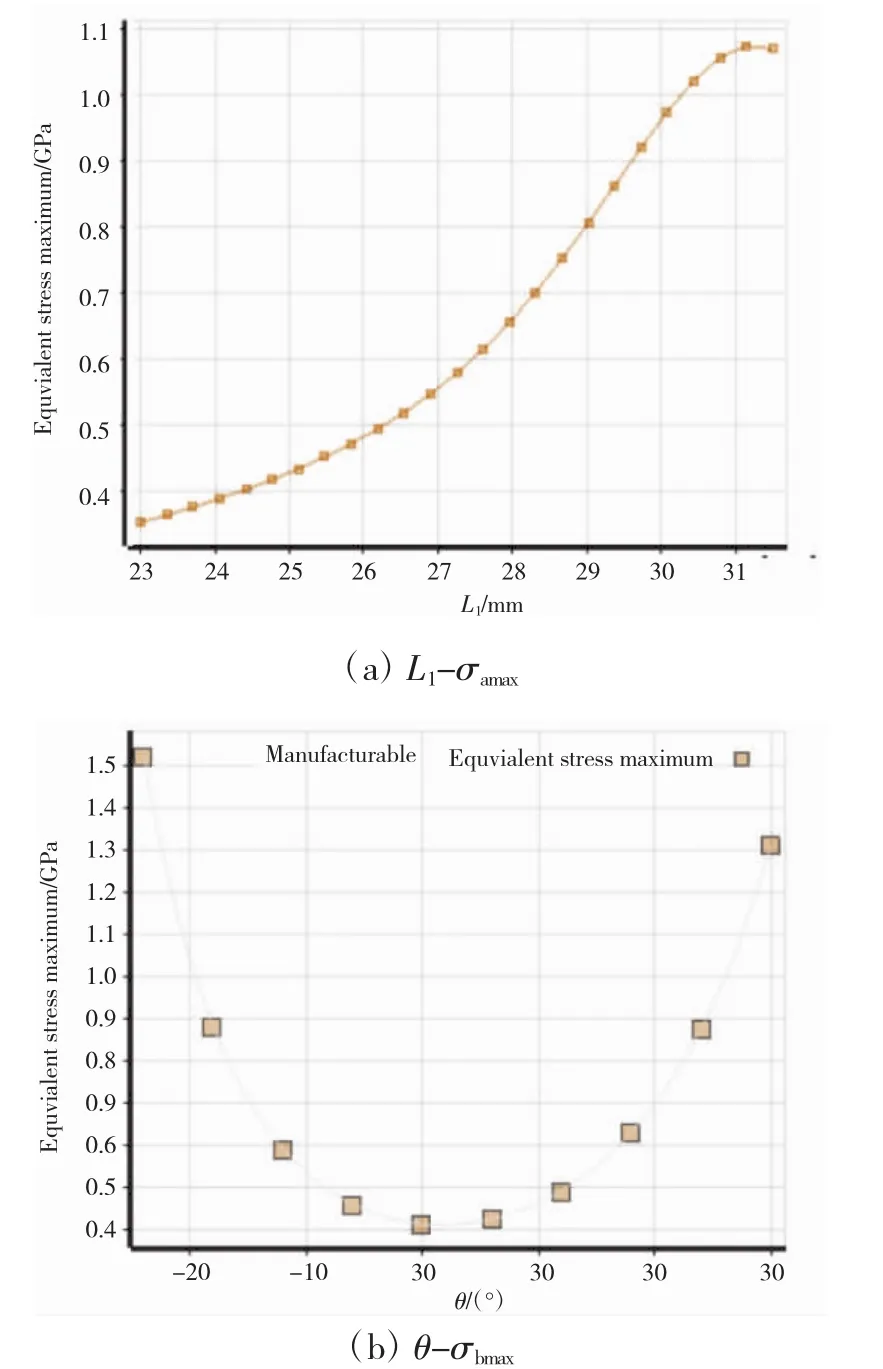
图6 响应面曲线关系

4 管线优化计算

4.1 管线优化模型

管线优化的目的是通过优化管线走向，补偿附加载荷产生的管路应力。本文使用19个控制点的坐标作为参数，绘制管线模型草图；再在管线模型基础上绘制管道3维实体模型；最后通过装配建立空气管路系统的3维模型，管线模型与实体模型如图7所示。

图7 结构建模思路

使用控制点对空气管路进行建模后，优化的边界条件和约束条件均可以用点的坐标、距离以及相对位置关系表达。图7管路实体模型中采用表3优化后的三通结构，使得对编号为10、11、12、sant2的控制点相对位置有约束，具体表达式如下

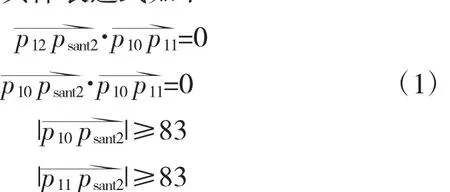
式中前2个等式约束限定点psant2为垂足，保证支管与主管轴线的正交关系；后2个不等式约束保证管段上有足够空间对三通进行焊接。挑选控制点的坐标作为设计变量，管路敷设空间、结构可变形范围、工艺规则的数学表达做约束条件，以最小化最大应力为目标，建立优化数学模型

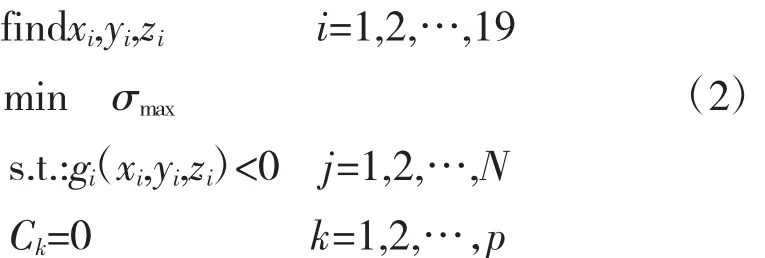
式中：xi、yi、zi为控制点坐标；σmax为管路最大应力。

4.2 优化计算与结果

考虑到管线优化模型参数过多，为了提高计算效率，先对其进行灵敏度分析，如图8所示。根据灵敏度分析结果，选择影响较大的19个参数作为设计参数，其他参数以定值作为输入，使用Workbench软件的Direct Optimization模块，随机抽取1000个样本，并使用筛选算法完成管线优化计算。优化前后应力应变对比见表4。

图8 最大应力关于特征参数灵敏度

表4 管线优化结果

表 4 中 σh1max、σh2max、σh3max分别为 3 个三通位置附加载荷应力最大值。通过优化管线走向，引气管路系统最大应力降低1.78%，最大应变降低15.81%，达到了优化效果。三通1和三通3位置附加载荷应力分别降低了25.83%和12.28%，管线优化的补偿效果明显。而与表2（c）相比较显示，管路优化使最大应力降低5.49%，最大应变降低14.76%。三通2位置附加载荷应力增大，说明以减小σmax为单目标做优化不能保证管路各处应力都减小；三通2位置总应力和总应变改变趋势与附加载荷应力不一致，这是优化后σh2max与σ2max位置不同造成的，如图9所示。

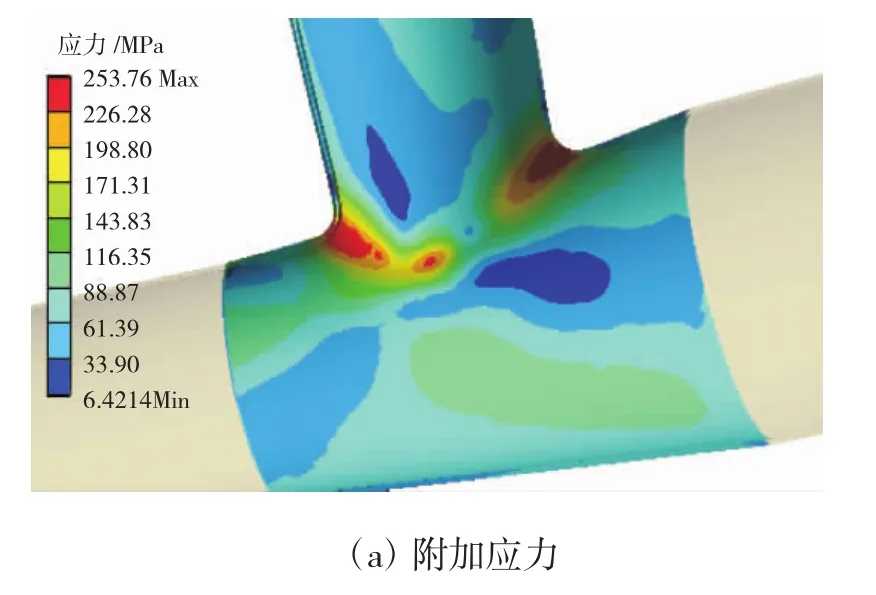
图9 三通2位置应力

从图9（a）中可见，管线优化后，三通2在腹部出现最大附加应力，而经全载荷弹塑性分析后，从图9（b）中可见，结构最大总应力出现在肩部。腹部受附加应力影响仍有较大总应力，但受压力载荷和结构变形影响，基于Mises屈服准则获得的总应力反而降低。图9中的结果进一步验证了管路系统弹塑性分析结果受加载过程影响。