基于虚拟激励法的薄板随机振动分析

齐鸣瑞，漆文凯，王文博

（南京航空航天大学能源与动力学院，南京210016）

0 引言

薄壁结构作为航空发动机及飞机的基本构件之一，各种约束条件下的计算研究受到国内外学者的普遍关注，应用不同方法对薄壁结构的弯曲振动进行研究，例如：Rao G V、Mirza W H、Kerstens J G M 等[1-3]采用有限元法、Narita Y、Kim C S 、Laura P A A 等[4-6]采用瑞利-李兹法、Li W L[7-8]采用改进的傅里叶级数法、贺国京等[9]应用能量泛函角度将位移量分离为静态位移和动态位移，研究了不同边界条件下矩形薄板的弯曲振动；陈英杰[10]以混合变量的形式求解了不同边界条件下受均布载荷的薄板弯曲情况；鲍四元、姚伟岸、邢誉峰等[11-13]采用辛对偶求解法获得了矩形薄板自由、受迫振动问题的通用解析解，克服了不同边界采用不同位移函数的传统弊端，明显提升了计算效率。

航空发动机以及飞机中的薄壁结构在实际使用过程中通常伴随着噪声的作用，噪声载荷是有一定频率特性的随时间、空间分布的随机压力载荷，从而会引起结构的随机振动。林家浩[14]提出的虚拟激励法（PEM）很好地解决了工程中研究复杂结构的随机振动方法中计算效率低、误差大的问题；许多学者[15-19]已经将PEM应用在航空航天、汽车制造、高速列车、海洋工程以及桥梁抗震等领域。与常规CQC（完全二次相组合方法）法以及SRSS（平方和开平方法）法相比，在随机振动研究中PEM由于其计算精度准确、效率高而广受欢迎。

本文利用改进的傅里叶级数法对位移函数和激励进行傅里叶展开，通过改变弹簧刚度模拟常用边界条件，利用PEM将白噪声激励构造成简谐激励，对动力学微分方程进行求解，计算结构位移响应功率谱密度，并将结果与有限元软件仿真进行对比。

1 理论模型

以矩形薄壁板为研究对象，如图1所示。在边界上设置横向位移约束弹簧和旋转约束弹簧，所有的经典边界条件（自由、简支和固支）都能通过指定弹簧系数设置为无穷大或零来获得。当约束横向位移方向弹簧的刚度值为无穷大，而约束旋转弹簧的刚度值为零，即可实现简支边界。

在噪声载荷 P（x，y，t）作用下，薄壁板受迫振动方

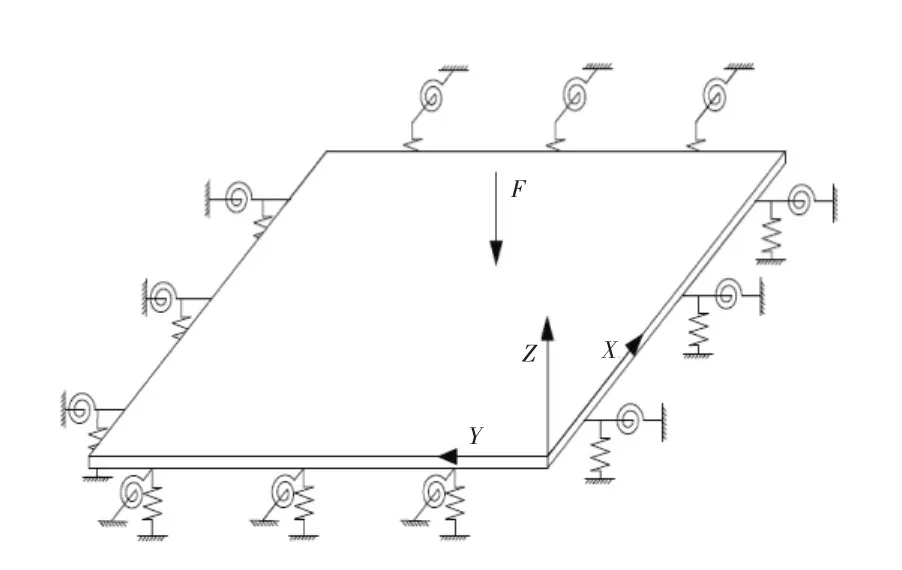
图1 薄壁板结构通用弹性边界模型

程为

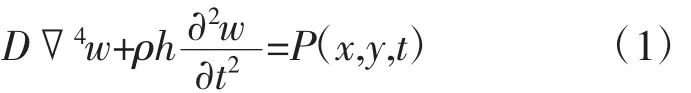
假设解的形式为

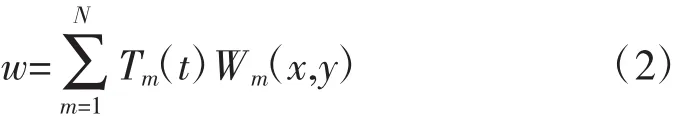
则矩形薄板的横向振动微分方程为

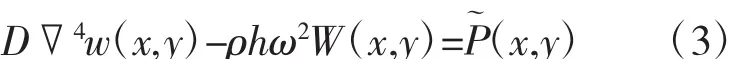
弹性支撑边界条件为

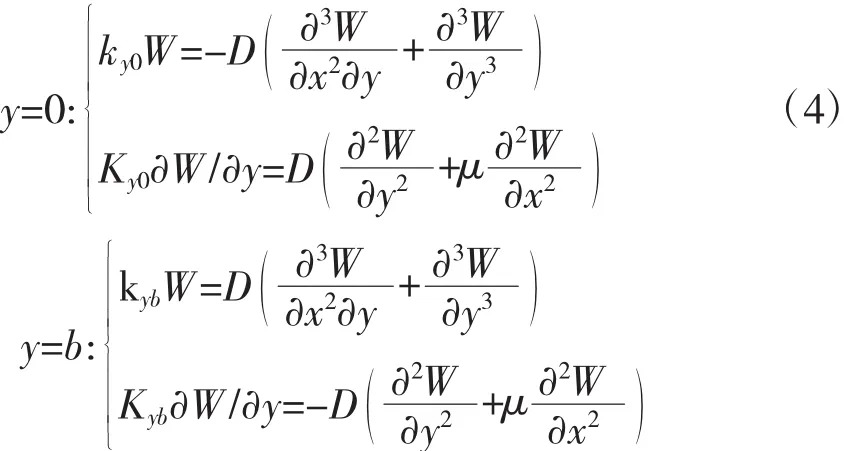
式中：k、K分别为横向位移约束弹簧和旋转约束弹簧的刚度系数，当k、K=∞时，表示固支约束；当k、K=0时，表示自由；当k=∞，K=0时，表示简支约束。通过改变k与K的数值，可以模拟不同的边界条件，提高了算法的通用性和计算效率。

2 位移函数

对薄壁板的位移函数进行改进傅里叶级数展开，表示成1个2维傅里叶双重余弦级数和8个辅助多项式的组合形式

假设关于x的辅助项为

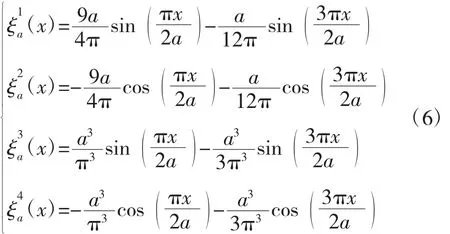
其满足

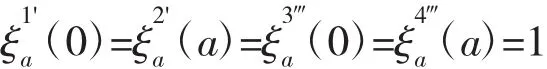
关于y的辅助项为

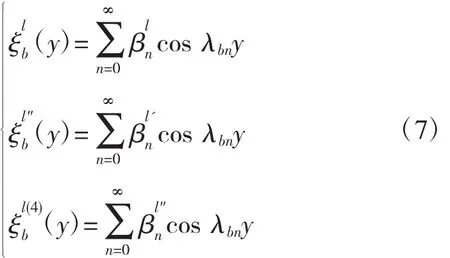
同样将载荷进行傅里叶展开为

其中，系数

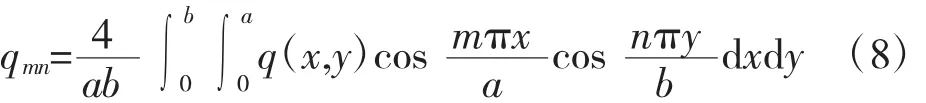
将位移函数（5）带入边界条件（4）及微分控制方程（3），并根据余弦函数的正交性，可得

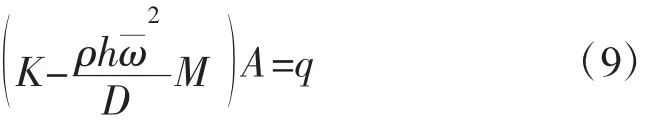
3 平稳随机响应算法

3.1 常规算法

目标结构施加均匀平稳的随机激励，采用模态振型叠加法求解动力学方程。考虑所有参振振型耦合项，通过频响函数计算结构的响应谱

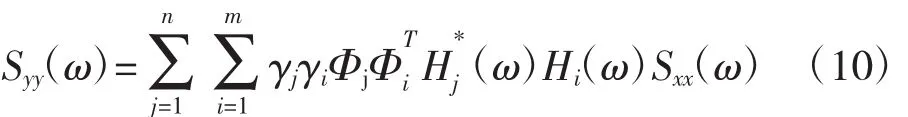
式中：γi、Φi、Hi（ω）、Sxx（ω）分别为第i阶振型参与系数、第i阶振型、频响函数和激励功率谱。

因为式（10）考虑了振型耦合，故称为CQC方法。使用模态振型叠加法（式（10））应用于复杂结构时，计算量较大。为减小计算量，对式（10）进行简化近似处理，忽略交叉项，得到

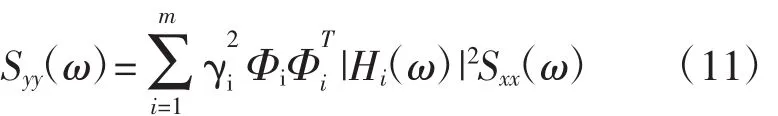
上述忽略模态振型耦合项的方法称为SRSS方法。虽然该方法效率高，但是不适用于大部分结构（尤其是3维结构）。

3.2 虚拟激励法

当单点平稳随机激励作用于线性系统时，记自谱密度为Sxx（ω），其振动响应的自功率谱为

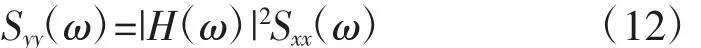
即响应矩阵共轭和响应矩阵转置相乘得响应谱矩阵。显然，虚拟激励法在精确度上与CQC法并无差距，但计算量大幅减小。此外应用虚拟激励法较方便，保证响应与激励之间为线性关系即可。

4 算例分析

取薄壁板算例，其薄壁板结构尺寸长宽高分别为510、270、1.3 mm，弹性模量 E=71 GPa，密度 ρ=2796 kg/m3，泊松比 μ=0.3。取中点处（x=0.255，y=0.135）的位移响应，计算响应功率谱密度函数，并将计算结果与文献[20]中的结果进行对比。

设有限带宽白噪声，其功率谱密度函数为S（0ω¯），其中声压级取 SPL=134 dB，Δω为带宽频率。

4.1 简支边界

取4边简支边界条件（k=∞，K=0），带宽频率为0～750 Hz，以涵盖结构前10阶固有频率，ANSYS谱分析取前10阶模态应用叠加法计算，见表1。

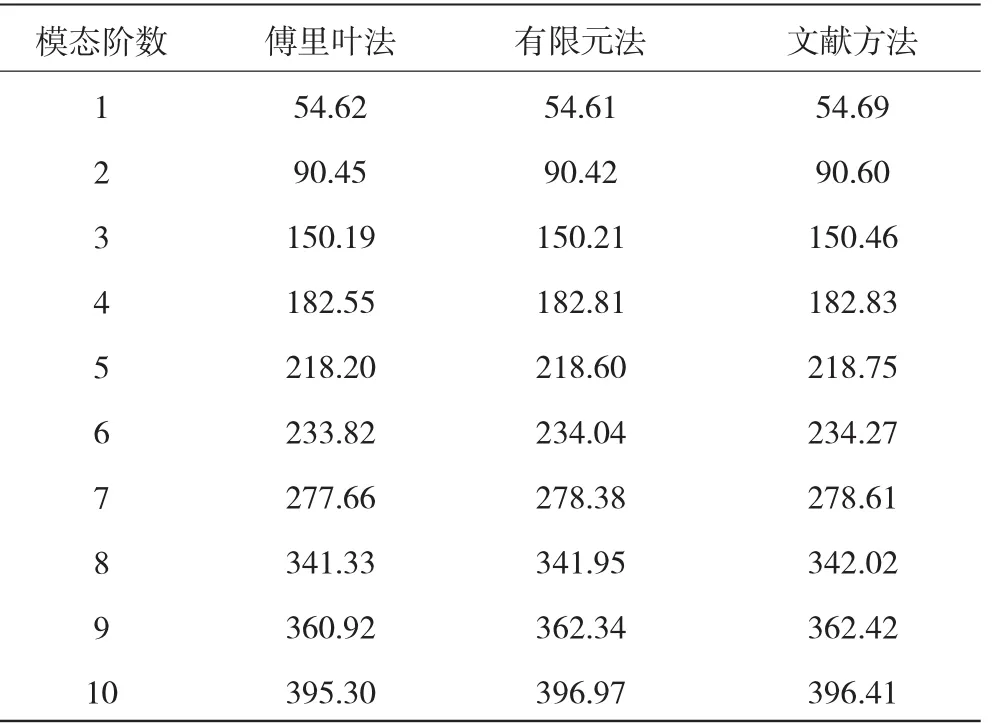
表1 简支边界前10阶固有频率对比 Hz

从表中可见，在简支边界条件下，3种方法求解出的前10阶固有频率在低阶处差别很小；而阶数越高，理论方法与有限元方法比较，结果偏小。

绘制中点处的位移响应功率谱，如图2所示。

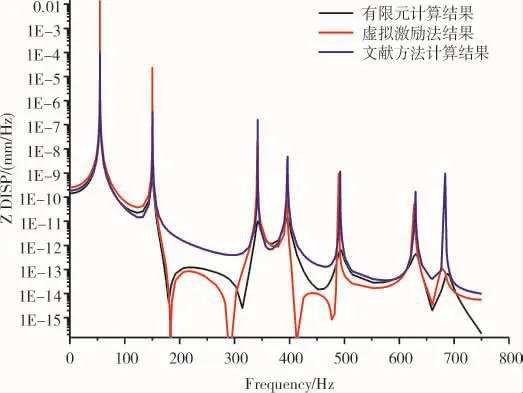
图2 简支边界下中点位置位移响应功率谱

从图中可见，采用虚拟激励法经过MATLAB编程和利用有限元软件自带谱分析模块算得的位移功率谱重合度较高，而利用文献中引入结合受纳函数的方法估算的位移响应功率谱在低谷处差距较大，这是由于结合受纳函数是通过用波长表示的薄板振型函数和假设结果表面声压为2维正弦波求得的，属于近似估算解，而虚拟激励法和有限元方法皆是对结构振动响应进行精确计算。3种方法计算位移响应功率谱曲线的峰值出现位置一致，分别是结构第1、3、8、10阶模态频率处，即 54.62、150.10、341.33、395.30 Hz处。

4.2 固支边界

4边设置固支约束（k，K=∞），带宽频率为 0～870 Hz，以涵盖结构的前20阶固有频率值，ANSYS谱分析时取前20阶模态结果，采用模态叠加法计算。

固支边界下前10阶固有频率对比见表2。从表中可见，固支约束下有限元方法求得的模态固有频率比理论解稍有偏差，且高阶处偏差较小。

绘制中点处的位移响应功率谱，如图3所示。

表2 固支边界下前10阶固有频率对比 Hz

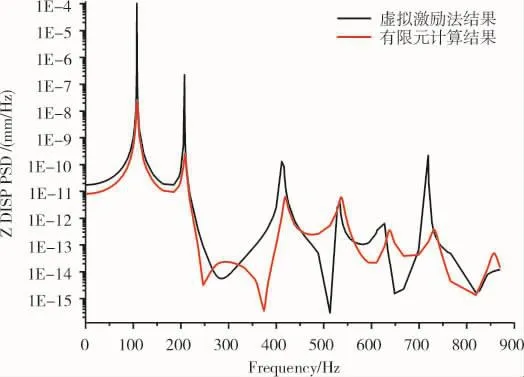
图3 固支边界下中点处位移响应功率谱密度

从图中可见，采用虚拟激励法经过MATLAB编程和利用有限元软件自带谱分析模块算得的位移功率谱在低频处重合度较好，高频部分差距较大，但是2种方法峰值出现时所对应的频率值相差很小，分别是各自结构的第1、3、8、10阶模态频率处。

比较上述2种边界条件下位移功率谱密度计算结果可得：

（1）位移响应出现多个峰值，表明响应是多模态的叠加，结构响应具有明显的多模态特征。

（2）位移响应功率谱曲线在研究频带范围内存在多个峰值，结合结构的模态频率值，表明这些峰值为相应位置处的模态频率处产生的位移响应，发生了结构共振效应，说明这些频率所对应的模态的参振系数较高，在结构分析时需加大关注度。

（3）基频处位移响应峰值最大，说明基频模态起主导作用。

5 结束语

本文结合改进的傅里叶级数法和虚拟激励法，对薄壁板进行了不同边界条件下的随机振动响应分析。将4边固支和4边简支边界下的位移函数用改进的傅里叶级数表示，并对激励进行傅里叶级数展开，利用PEM处理白噪声激励，实现了白噪声类型激励下的位移响应功率谱的理论推导和计算。利用有限元软件对相同条件下的薄板进行了模拟计算，并结合文献计算结果，将三者所得响应谱进行对比验证，发现本文方法较文献方法与有限元结果有更高的重合度，并验证了改进方法的准确性。同时通过使用弹簧代替经典边界条件，改变弹簧的刚度系数组合，可以高效准确地解决其他更复杂的结构以及边界条件，提高方法的适用性。