导流角和凹面腔深度对2级PDE中激波聚焦的影响

赵 坤 ，何立明 ，曾 昊 ，赵晨瑞 ，王 浩 ，张伟东 ，陈 月

（1.空军工程大学航空工程学院，西安710038；2.中国人民解放军某部队，河北沧州061700；3.中国人民解放军某部队，乌鲁木齐830075）

0 引言

2级脉冲爆震发动机（Pulse Detonation Engine，PDE）[1-2]是1种基于环形超声速射流对撞诱导激波聚焦起爆爆震的新型脉冲爆震发动机，由俄罗斯的Levin等首次提出，其工作过程中最重要的是连续超声速射流对撞诱导激波聚焦并起爆爆震，而激波聚焦的效果好坏是能否起爆爆震的关键。目前，国内外对凹面腔内激波聚焦进行了大量的试验和数值研究：美国的科研人员[3-4]发现在冷态条件下2维凹面腔内气流具有高频震荡的特点；日本的Taki等[5]研究了环形超声速射流对撞诱导激波聚焦起爆爆震的过程；空军工程大学的李海鹏、荣康、曾昊等[6-8]研究了环形超声速射流对撞诱导激波聚焦的过程机理以及结构和射流参数对激波聚焦的影响；南京理工大学[9-10]等也对激波聚焦进行了试验或者数值模拟并取得了一定成果。

但是目前聚焦机理尤其是各结构和射流参数对激波聚焦的影响规律还没有定论。为了促进2-Stage PDE的研究进展，必须把激波聚焦的机理及影响规律研究清楚。

本文基于冷态条件下开展了3维凹面腔内单循环激波聚焦的数值模拟，研究了导流角和凹面腔深度对激波聚焦的影响。

1 物理模型和计算方法

本文采用3维全尺寸模型进行数值模拟，其结构及尺寸如图1所示。在凹面腔中轴线上布置4个测量点用来测量压力和温度。采用FLUENT软件进行计算，初始网格尺寸δ=0.1 mm，并根据压力梯度自适应加密。射流入口设置为压力入口边界，pin=0.46 MPa，Tin=300 K，凹面腔内、外区域均为大气环境条件，pa=0.101325 MPa，Ta=300 K。所有壁面均为刚性、绝热、无滑移。数值模拟采用非稳态N-S方程、有限体积法、标准k-ε湍流模型、标准壁面函数。以空气为介质，在无反应条件下开展数值模拟。

图1 数值计算模型

为验证本文采用数值算法的有效性，采用文献[11]中的结构和参数进行数值模拟，并与试验结果进行对比，如图2所示。从图中可见，数值模拟结果与试验结果比较吻合，说明本文算法有效。

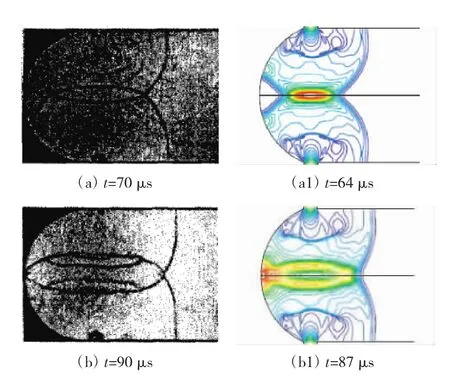
图2 文献试验结果与本文数值模拟结果对比

2 计算结果与分析

2.1 激波聚焦过程分析

为解释凹面腔内激波聚焦的过程，本文对导流角θ=15°、凹面腔深度dcav=20 mm条件下的数值模拟结果进行分析。模型对称面上激波聚焦过程的压力如图3所示。高压气体在射流喷管内加速到超声速并从其出口喷出，在压力差作用下压缩凹面腔内低压静止气体形成椭圆形的前导激波，如图3（a）所示；随后，在t=83 μs左右前导激波及其后的射流在凹面腔中轴线处对撞，如图3（b）所示；前导激波对撞后的反射激波与射流对撞后产生的激波相互耦合形成对撞激波，对撞激波左侧向凹面腔底部接近直到与凹面腔壁面碰撞后反射聚焦，使聚焦点的压力和温度升高，如图3（c）所示；经壁面反射的激波在聚焦后压力迅速降低并向尾喷管方向扩散，凹面腔内流场趋于稳定并进入下一循环，如图3（d）所示。

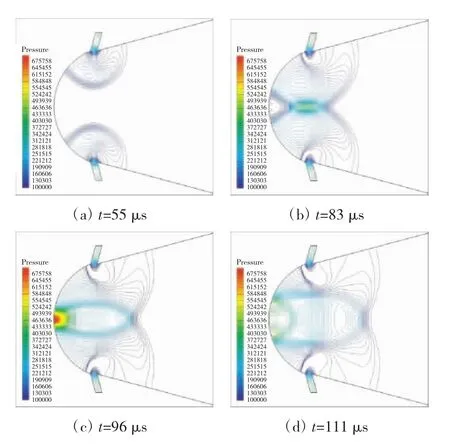
图3 激波聚焦过程压力

各测量点的压力变化曲线如图4所示。从图中可见，PC点的压力在t=85 μs时达到峰值，说明前导激波以及其后的射流此时在PC点附近对撞，导致对撞点的压力升高；随后距离PC点最近的PB点在t=91 μs时达到峰值，且比PC点的略大，这主要是因为左侧凹面腔封闭，激波及射流在向左侧运动的过程中，凹面腔内压力无法及时卸除；PD点的压力在t=97 μs时达到峰值，比PC点的峰值压力小很多，这是因为PD点靠近尾喷管外的大气环境，导致对撞激波在向尾喷管方向扩散时压力迅速降低；PA点压力在t=96 μs时达到峰值，此时对撞激波在凹面腔底部反射聚焦，导致压力大幅增加。在t=125 μs之后，各点压力基本平稳，说明此时凹面腔内流场基本稳定，第1个激波聚焦循环结束。根据各点压力的变化曲线所分析出来的规律与压力云图一致。

图4 各测量点的压力变化曲线

2.2 导流角对激波聚焦的影响

对于2级PDE而言，增大导流角可以使射流对撞点更接近凹面腔底部，并促进对撞激波向凹面腔运动，有利于激波聚焦，但是导流角的增大又会使对撞区域的能量降低，使对撞激波强度减小，不利于激波聚焦。本文在 dcav=30 mm 时，分别在 θ=0°、5°、10°、15°、20°、25°、30°时进行数值模拟，得到不同导流角时各测量点的峰值压力和温度，如图5所示。

从图中可见，4个测量点的峰值压力和峰值温度随着导流角的增大都呈现出先升高后降低的趋势。在PA点，θ=25°时达到最大值；在 PB点，θ=10°时达到最大值；在 PC、PD点，θ=5°时达到最大值。由于 PB、PC和PD点的峰值压力和温度是由对撞激波经过时导致的，所以这3个测量点峰值压力和温度随导流角的变化趋势基本一致，在较小导流角时峰值压力和温度最高；而PA点的峰值压力和温度是由对撞激波反射聚焦所导致的，所以其变化趋势与其余3点处的不同，在较大导流角时峰值压力和温度最高。

图5 不同导流角时各点峰值压力和温度

鉴于射流对撞区域和激波聚焦区域的峰值压力和温度更能反映激波聚焦效果，本文对PA和PC点的峰值压力和温度进行详细分析。从图5（c）可见，在θ=5°～30°，随着导流角的增大，射流对撞区域（PC点）的峰值压力和温度逐渐降低（说明对撞区域能量减小），且降低的幅值逐渐增大，尤其是在θ=30°时降低的幅值最大；从图 5（a）中可见，在 θ=0°～25°，随着导流角的增大，激波聚焦区域（PA点）的峰值压力和温度逐渐升高，但是升高的幅值逐渐减小，这是因为此时射流对撞点能量减小，对撞激波强度减小，而在θ=30°时射流对撞区域能量的大幅减小导致了激波聚焦的峰值压力和温度开始降低。综上所述，导流角过大或者过小都不利于激波聚焦，在θ=25°时激波聚焦效果最好。

2.3 凹面腔深度对激波聚焦的影响

凹面腔深度越大，对撞激波在向凹面腔底部运动过程中的能量损失越大，不利于激波聚焦。但是对于开口直径不变的球型曲面而言，凹面腔深度增大时曲率也会随之增大，而曲率越大就会使激波反射后更容易聚焦。本文在θ=15°时，分别对dcav=20、25、30 mm时的工况进行数值模拟，得到不同凹面腔深度时各测量点峰值压力和温度，如图6所示。

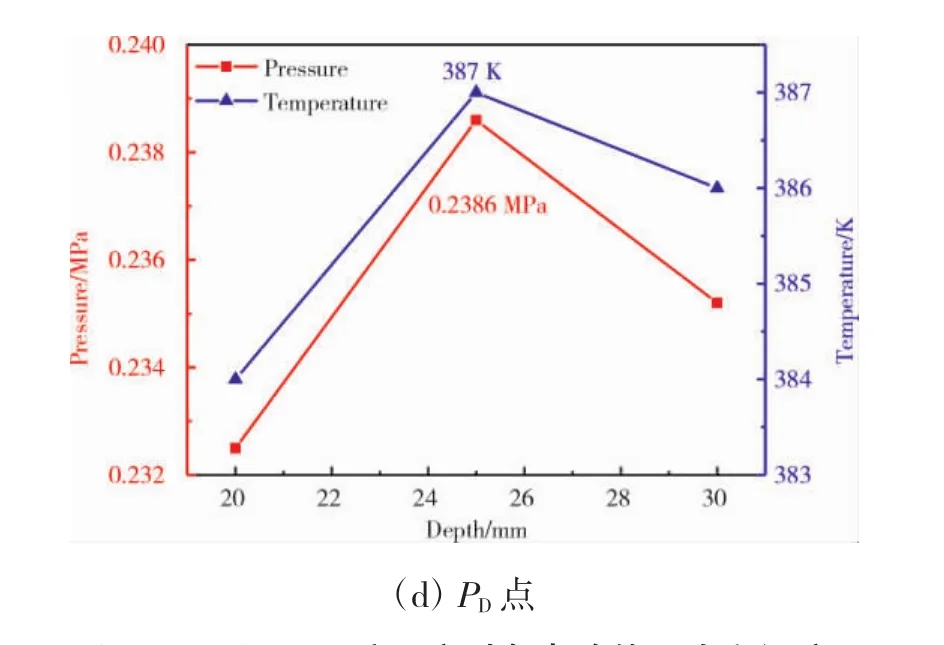
图6 不同凹面腔深度时各点峰值压力和温度

从图中可见，不同凹面腔深度时PC点的峰值压力和温度相差不大，说明凹面腔深度对射流对撞的影响不大；PD点位于尾喷管内，受凹面腔深度的影响比较小，所以峰值压力和温度变化也不大；PB位于凹面腔内，凹面腔越深，射流向凹面腔内填充导致的压力升高值越小， 其峰值压力和温度随凹面腔深度的增大而降低；对比PA点的结果发现，在dcav=25 mm时峰值压力和温度最高，本文分析认为，此时的峰值压力和温度高于dcav=20 mm时的主要原因是凹面腔曲率大有利于聚焦，而dcav=30 mm时的峰值压力和温度小于dcav=25 mm时的主要原因是对撞激波传播距离长，能量损失大。综上所述，凹面腔深度过大或者过小都不利于激波聚焦，在dcav=25 mm时激波聚焦效果最好。

综上所述，导流角和凹面腔深度都对激波聚焦的效果造成较大影响，实际上凹面腔其他结构参数的变化同样会影响激波聚焦效果。如果改变凹面腔开口直径、尾喷管角度和长度等参数，可能会得到不同计算结果，但是基本规律是适用的，即导流角和凹面腔深度过小或者过大都不利于激波聚焦。

3 结论

本文以空气为介质在冷态条件下开展3维凹面腔内激波聚焦的数值模拟，得出如下结论：

（1）合适的导流角有利于激波聚焦，在dcav=30 mm、θ=25°时凹面腔底部的峰值压力和温度最高，激波聚焦效果最好。

（2）合适的凹面腔深度有利于激波聚焦，在dcav=25 mm、θ=15°时凹面腔底部的峰值压力和温度最高，激波聚焦效果最好。

（3）本文仅采用数值模拟方法进行研究，并不能全面、准确地反映激波聚焦机理，后续将通过试验方法继续研究。