空间万向传动当量夹角的计算和优化设计

田中旭，祁 平，高学峰

（1.上海海洋大学 工程学院，上海 201306；2.中国北方发动机研究所，山西 大同 037036；3.蒂森克虏伯汽车系统计算有限公司，上海 201201）

1 引言

十字轴万向节因其可靠性高，成本低廉，仍得到了广泛的应用。当前，含万向节的传动轴在运动学[1]与强度[2]方面仍然存在很多值得研究的问题，这些问题的关键点在于万向节两侧的传动轴存在一定夹角。在含多万向节的传动轴中，综合评价传动轴布置的参数就是当量夹角[3]。在万向节传动当量夹角不为零时，传动轴的转速将产生波动[4-5]，同时还在传动轴上产生波动附加弯矩作用[6]。转速的波动会引起传动系统的齿轮啮合冲击和噪声，影响其可靠性；附加弯矩则会引起传动轴中间支撑的振动，会进一步引起设备或车辆的振动和噪声[7]，同时也易引起传动轴本身的弯曲振动。因此，传动轴当量夹角的设计和控制，是传动轴布置中最为重要的指标之一[8]。而当量夹角的准确计算则是传动轴设计和优化的前提和基础。含多万向节的传动轴布置往往因各种条件限制，不完全在同一个平面内，即形成了一种空间布置。此时，当量夹角的计算会变得复杂，也非常容易出现计算错误，难以为传动轴的设计提供有利支持，同时为进一步的传动轴布置优化带来风险[9-10]。

文献[3，11]给出了两种准确的当量夹角计算公式，然而在应用中，准确计算当量夹角仍然非常困难，其主要原因在于，实际传动轴布置的描述方式，与当量夹角计算中的初相位和传动轴的夹角参数不一致，在计算这些参数时常常产生错误。首先，因传动轴空间布置，使得传动轴的真实夹角计算变得复杂；其次，计算当量夹角所需的各个万向节叉初相位，已经不能再简单由传动轴两侧万向节叉的相位关系来依次确定，应该由真实的空间位置来准确计算。目前，还未发现在精确计算万向节叉初相位和传动轴空间夹角计算上的当量夹角计算模型，人们多采用传动轴两侧万向节叉的相位关系和传动轴在竖直面内的夹角，来直接给定这些参数，常常带来较大计算误差。依据传动轴设计习惯，研究了当量夹角相关参数的描述和计算方法，并在此基础上研究了空间当量夹角的计算方法和验证手段，并给出传动轴最优布置计算方法，为传动轴的设计提供了可靠的计算基础。

2 传动轴布置的描述方法

在传动轴设计中，一般给出了传动轴吊架或支架、变速箱等动力输入端、传动轴的动力输出端等位置坐标；在传动轴万向节叉的方向方面，一般给出每跟传动轴两侧万向节叉平面的角度，并在多实际中采用两侧叉平面为0°和90°两种方式的传动轴。

对于由主动轴i和从动轴i+1组成的某万向节i，如图1所示。设主动轴万向节叉所在平面为Bi，从动轴万向节差所在平面为Bi+1，平面Ai和平面Ai+1为两竖直平面，并分别包含主动轴和从动轴轴线。在当量夹角的计算过程中，为了对传动轴布置进行准确描述，这里给出如下方式描述传动轴的布置（其中动力传动的方向为x轴方向）：（1）对于由n个传动轴组成的传动轴系统的位置和方向，采用各个万向节十字轴中心坐标（xi，yi，zi）（i=0，1，…，n）来描述，其中在传动轴系两侧的输入轴和输出轴上各增加一个点（0点和n点），即（x0，y0，z0）和（xn+1，yn+1，zn+1），用来表达输入轴和输出轴的方向。（2）采用各个万向节主动叉平面Bi与竖直面Ai所成的角度βi（i=1，2，…，n），来表达万向节叉的方向，其中沿传动方向导前为正，导后为负。因传动方向非常接近x方向，所以如此表达万向节主动叉平面具有非常高的精度，而且计算起来非常方便，当知道第一个叉平面与竖直面所成角度，以及各个传动轴两侧叉的角度，便可准确计算出各个βi（i=1，2，…，n），以后的计算和验证中也证实了这一点。

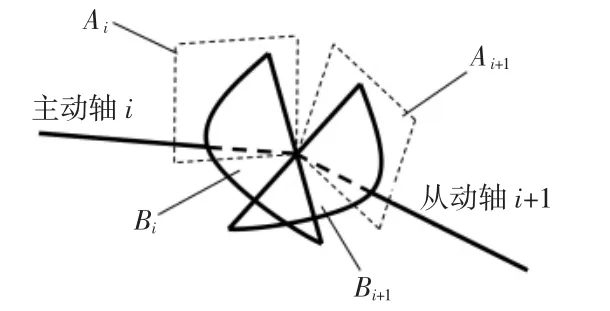
图1 万向节示意图Fig.1 Sketch Figure of Universal Joint

3 传动轴空间当量夹角的计算

文献[11]针对空间布置的多万向节传动轴，通过输入轴与输出轴之间的运动学关系分析，导出了空间传动轴当量夹角θe的计算公式

式中：θi—第i个万向节两侧的主从动轴之间的夹角（i和i+1之间的夹角）；αi—第i个万向节初相位，即主动叉平面Bi与两侧传动轴的轴线（i和i+1）所成平面夹角，导前为正，导后为负。因此，计算当量夹角的关键便是计算各个θi和αi，以下将给出具体计算方法。

各传动轴的轴线单位矢量为：

式中：li—传动轴的长度，其计算公式为：

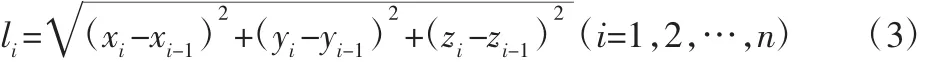
则对各个万向节两侧传动轴夹角θi有：

在计算中，如果θi足够小，则万向结两侧可以认为是一根传动轴，转速也不会波动，此时只需令θi=αi=0即可。

以下计算各个万向节初相位。根据βi（i=1，2，…，n）的定义，可得到主动叉平面法线单位矢量ti为：

主动轴和从动轴所在平面的单位法矢量为：

则初相位角可以如下求出：

式中：i—x向单位矢量。（7）式中的第一个因式起到了取符号的作用，即沿x正向，并按右手定则，导前为正，导后为负。

计算出各个轴线的夹角和初相位后，应用式（1）便可计算出传动轴的当量夹角。

4 当量夹角算法的运动学仿真验证

由于试验方法受到诸多条件限制，而且测量也会带来难以预期的误差。因采用动力学仿真软件，进行传动轴的运动学仿真可得到近似精确的运动学关系，可以方便地对当量夹角算法进行验证，即通过运动学仿真检验传动轴系统输入和输出转速之间是否满足

式中：ω1、ω2max和 ω2min—输入转速、输出转速最大值、输出转速最小值。

采用了UGMotion来实现传动轴的运动学仿真，来进行当量夹角计算的验证。某商用车传动轴当量夹角计算和仿真结果的比较，如表1所示。其中，也给出了当前企业常用的几种方法得出的计算结果。该传动轴系统含三个万向节，其传动轴布置参数，如表2所示。

表1 各算法当量夹角计算结果Tab.1 Calculation Results of Equivalent Angle of Each Algorithm

表2 某商用车传动轴布置参数Tab.2 Parameters of a Commercial Vehicle Transmission Shaft

对于企业常用的三种常用的算法说明如下：

4.1 X-Z平面投影法

X-Z平面投影法是把空间传动轴布置，看成xz平面内的平面布置，初相位以传动轴两侧万向节叉的相位作为初相位的直接计算依据，误差来原因在于没有考虑到传动轴的空间布置。

4.2 空间I算法

和X-Z平面投影法唯一的区别就是使用了轴线的空间夹角代替平面夹角，计算精度有所提高，但初相位的计算还是和X-Z平面投影法一样，误差在所难免。

4.3 空间II算法

空间II算法和空间I算法的唯一差别就是初相位的计算上。空间II算法上考虑了万向节导前角对初相位的影响。但依然没有照初相位的定义来进行计算，同样可能产生不可估量的误差。由表2的计算结果可以看到，不采用更为准确的当量夹角计算方法，常常会产生比较大的误差，这里建议采用给出的计算方法，已获得比较高的计算精度。

5 传动轴的优化布置计算

在传动轴设计中，可调整的主要是中间支撑点的位置[12]，它决定了附近万向节的位置和传动轴的长度，这里采用万向节十字轴中心坐标为优化设计变量，并考虑传动轴两侧万向节叉的各种相位角[13]情况对当量夹角的影响。这里以上节给出的商用车传动轴设计为例，寻求最优的传动轴设计方案。在传动轴设计时，设计目标是当量夹角尽可能小同时，同时需要兼顾空载、满载等情况，可如下设计优化的目标

式中：θek、θem—空载和满载情况下的当量夹角；Wk、Wm—空载和满载情况下的权系数，可根据两种情况下的侧重程度取值。

因传动轴优化布置时，还存诸多约束和限制，如对各个设计参数采用取整，中间支撑安装限制等。其中比较重要的方面是单个传动轴不要过长，以免其弯曲振动固有频率过低。在传动轴数量固定的情况下，传动轴长度约束条件可如下表达：

式中：Li—任意传动轴长度；L—传动轴的传动距离；n—传动轴数。其中，r—阈值，其确定依据为：当传动轴长度为L/n+r以下，传动轴最小固有频率满足传动系统要求。

而且算法效率比较高情况，所以可采用全区间扫描的方式，寻求更优的设计参数，而且结果非常可靠。经过扫描，给出了新的布置方案：第二万向节十字轴中心坐标为（2746，5，299），两个传动轴两侧万向节叉相位角度均为。优化前后的当量夹角，如表3所示。可以看出，改进后的传动轴布置，使得当量夹角大幅度缩小。

表3 改进前后的当量夹角Tab.3 The Equivalent Angle Before and After the Improvement

6 小结

在传动轴当量夹角的计算中，如传动轴空间布置，则给传动轴当量夹角计算带来困难，当前常用的方法易得到不准确的计算结果。而影响计算精度的根源在于，传动轴的夹角和初相位严格准确的描述和计算。给出非常精确的当量夹角计算方法，并给出了传动轴最优设计方案的计算方法。算例表明，算法对传动轴当量夹角的计算和优化布置是非常有效的。