全景相机转台低重力补偿装置研究

杨 毅 ，常 勇 ，王洪光 ，景凤仁

（1.中国科学院沈阳自动化研究所 机器人学国家重点实验室，辽宁 沈阳 110016；2.中国科学院大学，北京 100049）

1 引言

随着人类太空探索活动的增多，空间机器人在承受太空中恶劣环境、扩大人类空间活动能力、提高安全性、和经济效益等方面的优势受到世界各国的重视[1]。空间机械臂是太空活动中常用的机器人设备，为了保证空间机器人在太空中准确完成各种任务，在地面模拟空间机器人低重力、零重力以研究其各项物理性能是一个很重要的研究内容。目前常用的地面机械臂低（零）重力模拟方法有：气浮法、水浮法、吊丝法[2-3]。

气浮法是利用喷气推力的反作用力抵消机械臂重力。气浮法结构简单、使用方便，但仅能提供两自由度2维空间内的功能测试，对机械臂的运动形式有一定要求。文献[4]研制的SSRMS地面实验系统、文献[5]开发的双臂自由飞行空间机器人系统以及文献[6]双臂自由飞行机器人系统，均使用了气浮法进行相应的地面重力补偿实验研究。

水浮法是利用水产生的浮力，并通过适当的配重使空间机器人系统在水中悬浮，即通过水的浮力来补偿机器人的重力影响。该方法能实现空间机器人三维工作空间上的物理仿真，但系统密封性要求高、设备维护费用高。国外大学的漫游者NBV和某智能机械研究所空间机械臂进行了水浮法研究[7-8]。

吊丝法是利用吊丝拉力抵消机械臂重力的一种方法，吊丝拉力由配重块重力或滚筒主动收放吊丝产生的拉力提供。根据吊丝拉力跟随实验物移动的情况，吊丝法可分为主动式和被动式。吊丝法可实现机械臂三维空间重力补偿，主要依靠平面跟随装置及滚筒收放吊丝装置，系统较复杂。国外某大学采用此方法对空间机械臂进行了重力补偿实验研究[9-10]。

针对月球表面探测的全景相机转台的重力补偿开展研究。该转台机构相对简单，结构紧凑，现有的重力补偿装置很难满足要求，根据转台机构和结构特点，设计了一种主动式吊丝重力补偿装置，该装置包括补偿操作臂、吊丝配重单元和力传感器单元，通过补偿操作臂与转台同步运动，实现全景相机转台的重力补偿。

2 低重力补偿机构方案分析

2.1 全景相机转台

全景相机转台搭载在月球探测器上，末端负载为全景相机，如图1所示。全景相机转台方位轴、俯仰轴的轴向分别沿垂直于和平行于水平方向，但并不正交。方位关节的定子固定于基座，转轴连接俯仰关节的定子，俯仰关节的转轴连接负载（即相机）。

图1 全景相机转台Fig.1 Panoramic Camera Turntable

2.2 吊丝方案分析

转台各连杆的到转轴尺寸很小，运动精度要求较高。因此转台的重力补偿装置要求结构简单、控制方便且满足重力卸载精度要求，基于重力补偿方法的调研分析，选定吊丝配重方案实现转台的重力补偿。

为减少装置的复杂度，初步方案，如图2（a）所示。操作臂支撑吊丝系统，且与转台方位关节同步运动；转台方位臂由悬挂在操作臂上的滑轮、吊丝和配重块进行重力补偿，运动中吊丝保持竖直；转台俯仰臂由滑车、滑轮、吊丝和配重块进行重力补偿，吊丝在滑车主动调节下保持竖直。图2（a）可以实现转台两个机械臂的重力补偿，此方案不足：由于转台尺寸较小，滑车系统较为复杂，控制精度不易于满足要求，且俯仰臂配重块上下有移动。

补偿操作臂与转台机构相同，操作臂各关节与转台对应各关节同步运动，如图2（b）所示。补偿操作臂俯仰轴连杆有两个滑轮支撑吊丝，通过配重块对转台俯仰轴负载进行重力补偿。该方案存在不足：当俯仰臂非水平位置时吊丝非竖直，影响重力补偿精度，且配重块上下有移动。

为了减少转台俯仰轴吊丝配重块上下运动的影响，补偿操作臂俯仰轴两滑轮中心相对转台俯仰轴及俯仰轴负载质心位置在水平位置上相差小滑轮半径r，如图2（c）所示。两个小滑轮圆心、转台俯仰轴和俯仰轴连杆吊点在同一平面内组成平行四边形结构，当操作臂与转台各关节同步运动时，两套吊丝配重单元吊丝始终保持竖直，配重块上下无移动。

图2 三种低重力补偿方案Fig.2 Three Kinds of Low Gravity Compensation Scheme

2.3 平行四边形重力补偿机构分析

俯仰臂吊丝低重力补偿装置使用一个自由度解决了转台俯仰臂三维空间内的重力补偿以及配重块上下移动的问题。如图3所示。o22的水平位置相对于o12的位置偏移滑轮半径r，即连杆o11o12长度较连杆o21o22的长度长r，o12o13o21o22组成平行四边形机构。o13为转台俯仰臂负载质心位置也是吊丝点，a1、a2、a3、a4为吊丝与滑轮的切点。滑轮o22和滑轮o23半径相等。令a1到吊点o13的吊丝长度为d，其中，lo12o13长度为l3。

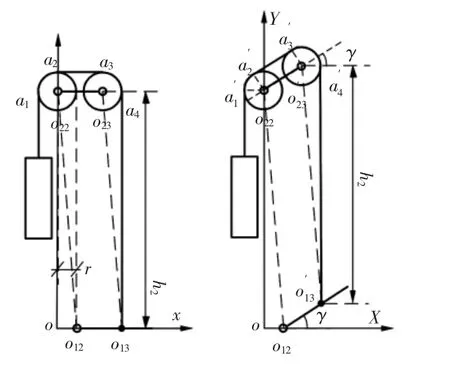
图3 平行四边形原理图Fig.3 Principle Diagram of Parallel Quadrilateral

所以a4o13垂直X轴。

式中：h2—吊丝长度；l3—o12到 o13的距离；r—滑轮半径。

在o12o13o22o23平行四边形结构中，当俯仰臂水平时，吊丝与两个滑轮之间包角之和为180°；当转台俯仰轴和同步臂俯仰轴同向转动角度γ后，左边滑轮与吊丝的包角减少（增加）γ，而右边滑轮与吊丝的包角增加（减少）γ，两个滑轮与吊丝的包角为180°。所以当俯仰臂转动角度γ后，a4o13吊丝保持竖直，配重块质心Y轴位置不变，若两滑轮为全滑动，则两滑轮相对于杆o22o23没有转动。因此，方案在运动期间支撑臂、配重块及吊丝对转台影响较小。

2.4 低重力补偿装置模型设计

为了保证低重力补偿方案重力补偿精度，结构上需要保证吊丝吊点、吊丝配重块质心及重力补偿对象质心在同一平面内。另外，转台质心位于左右对称线上，各机械臂满足刚度要求。

系统方案主要包括操作臂、吊丝配重单元、全景相机转台、控制单元和隔振平台单元，如图4（a）所示。模型中全景相机转台与实际全景相机转台外形不同，但质量、质心分布相同。为了保证控制的精度，各关节均有两个角度传感器，一个检测关节转角，另一个检测电机转角。

转台方位臂由驱动单元、圆光栅、编码器和臂体组成，俯仰关节驱动单元安装于方位臂一侧，编码器及配重块安装于另一侧，保证了方位臂质心位置居于中间，如图4（b）所示。此时转台方位臂质心相对于方位轴距离较大，因此，在转台方位关节处增加配重块，调节质心位置。全景相机转台安装在六维力传感器上，为保证其检测转台力和力矩的准确性，转台不能增加自身之外的结构支撑。如图4（b）所示，在转台方位关节驱动单元上安装两个轴承，轴承内侧为电机外壳及减速器外壳，轴承外侧为方位臂外壳及轴套，使用不与外侧接触的圆光栅对关节转角进行角度检测，这种设计不仅增加了转台结构的可靠性，同时使六维力传感器不受外力干扰。

3 误差分析

全景相机转台低重力补偿装置采用的是主动式吊丝卸重，补偿操作臂与转台需要同步运动才能使吊丝竖直，保证重力补偿精度。但实际运动控制过程中，补偿操作臂与转台运动一致性很难保证，关节存在偏角，影响重力补偿精度。

由于控制误差，操作臂与转台方位臂转角产生偏角，引起吊丝竖直偏角，如图5所示。图中：R—同步臂滑轮半径；h1—吊丝与滑轮切点到吊丝与机械臂连接点长度；d1—上臂吊丝吊点偏移距离。当操作臂方位臂与转台方位臂存在夹角α1时，切点b以方位轴为圆心，旋转α1角度后到达切点b′，吊丝竖直方向产生夹角β1。吊丝带动滑轮转动产生的摩擦力f1，方向与滑轮转动方向相反。

重力补偿精度为：

式中：m1—配重块质量；

M1—转台方位轴连杆质量；

f1—滑轮摩擦力。

图5 方位关节转角误差图Fig.5 Azimuth Joint Rotation Angle Error

转台俯仰臂、操作臂俯仰臂旋转γ角，由于存在控制误差操作臂俯仰臂实际旋转γ±α2，如图6所示。q2、q3和q4是滑轮与吊丝的切点，角α2较小、h2相对滑轮半径r较大，认为q3和q4切点分别于在同一水平面。四边形和四边形为平行四边形，所以边长等于边长 q2q3，边长等于边长q2q4。由操作臂的俯仰臂和转台的俯仰臂夹角引起的吊丝竖直夹角为直角三角形p2cq3、直角三角形p2q2e的顶角β21、β22。

图6 俯仰关节转角误差图Fig.6 Pitch Joint Rotation Angle Error

吊丝竖直夹角的大小与滑轮o23圆点理论点和实际点的距离在水平线上的投影大小成正相关。当竖直线平分误差角时滑轮o23圆点理论点和实际点的距离在水平线上的投影最大。

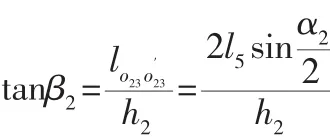
转台俯仰臂重力补偿精度为：

式中：m2—配重块质量；M2—转台俯仰轴负载质量，摩擦力f2大小根据α2相对γ偏角方向确定。

如图7（a）所示，同时考虑误差偏角α1和α2时吊丝竖直偏角示意图。其中实线为无误差状态下的操作臂和转台位置，操作臂的方位臂相对转台的方位臂存在误差α1，X轴平分α1角，操作臂的俯仰臂相对转台的俯仰臂存在误差α2。q1、q2和q3为吊丝与滑轮的切点，角α2较小、h2相对滑轮半径r较大，认为q3和q4切点分别于o′23和o″23在同一水平面。p1为吊丝在转台俯仰臂上的吊点，p2、p3分别是q2、q3在转台俯仰臂上的竖直投影点。l1是转台方位轴到吊点的长度，l2是转台方位臂长度，l3是转台俯仰臂吊丝吊点到转台俯仰轴距离，l4是操作方位臂长度，l5是操作俯仰臂顶端滑轮圆点到操作臂俯仰轴距离。

图7 操作臂、转台转角误差图Fig.7 Operating Arm、Turntable Rotation Angle Error

结合图6、图7分析可知，在α1和α2误差下吊丝在转台俯仰臂上的吊点（图7（a）中p1点）可以看作是由α1误差下吊丝在转台俯仰臂上的吊点p2转移至p1。面上的投影点，角β2是在α1和α2误差下俯仰臂吊丝竖直偏角，如图 7（b）所示。长度等于ac长度。

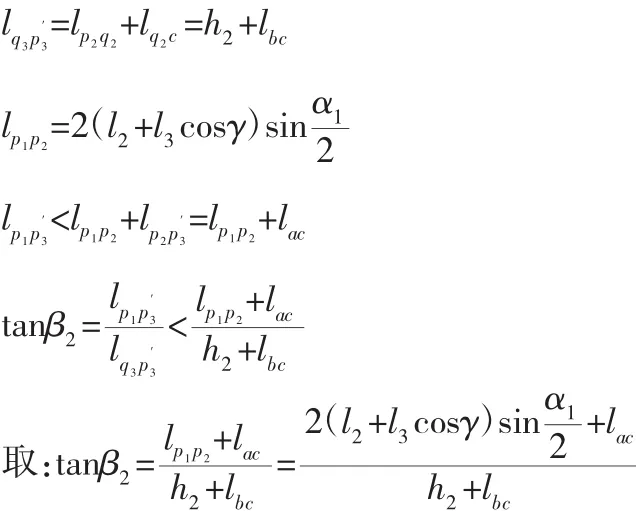
由图 7（b）可知，loc为 lo23o′23在水平面的投影长度，lbc为在竖直线上的投影长度，俯仰臂转动时lac与lbc成反向变化。由公式X 可知，当 lac最大、lbc最小时 tanβ2最大，即 o23o′23或 o23o″23平行于水平面时最大。

在同时考虑误差角α1和α2下，转台俯仰轴负载重力补偿精度为：

通过上述分析可知，在俯仰臂转角γ、方位臂转角误差α1、俯仰臂转角误差α2、各臂长l、各配重块质量m以及各连杆质量M已知下，方位臂吊丝重力补偿精度与滑轮半径R、吊丝高度h1及滑轮摩擦力f有关，俯仰臂吊丝重力补偿精度与h2有关。上述分析为低重力补偿系统中吊丝竖直长度的设计提供了依据。

4 仿真研究

在完成吊丝配重补偿机构设计与分析后，针对平行四边形机构及低重力补偿方案进行了仿真实验，以验证平行四边形机构特点的正确性和系统重力补偿精度、力矩补偿精度。

4.1 仿真模型

利用SolidWorks软件对系统模型进行简化，简化后模型质心和质量与三维模型相同。将简化后的模型导入Adams软件，设置模型之间运动关系及吊丝系统。配重块质量为重力补偿对象质量的5/6，吊丝吊点在相应质心处。仿真实验分两部分，g条件下全景相机转台低重力补偿装置仿真实验和1/6g条件下全景相机转台仿真实验，然后对两次仿真实验数据进行对比分析。仿真各关节运动形式，如图8所示。

图8 系统仿真模型各关节速度Fig.8 System Simulation Model Joint Velocity

4.2 仿真结果分析

如图9（a）可见，两个配重块质心在竖直方向的位置没有因转台的转动而发生大的变化，证明方案中平行四边形结构的机构特点。锚点1、锚点2为全景相机模拟转台俯仰臂重力补偿吊丝两端连接点，锚点3、锚点4为全景相机模拟转台方位臂重力补偿吊丝两端连接点。如图9（b）所示，通过Adams分析得出，锚点1与锚点2受力最大差值为0.001N，锚点3与锚点4受力最大差值为0.0015N。由于吊丝经过滑轮，吊丝与滑轮的静摩擦造成吊丝两端拉力不同。

式（6）是重力补偿精度公式。

式中：F差值—实际拉力与理论拉力差值；M—被补偿对象质量。

转台方位臂重力补偿精度为0.003%，转台俯仰臂重力补偿精度为0.04%。六维力传感器位于全景相机模拟转台底座下面，检测转台在重力补偿后的竖直重力及倾覆力矩。由图9（c）可知，在1/6g条件下由六维力传感器竖直受力可得转台重力10.348N，在g条件下由六维力传感器竖直受力可得转台重力10.354N，转台整体重力补偿精度为0.012%。式（7）为倾覆力矩卸载精度及转矩补偿精度。

式中：T差值—实际力矩与理论力矩的绝对值；T5/6—理论力矩的5/6。

倾覆力矩是指由转台方位臂重力相对于转台底座引起的力矩。倾覆力矩补偿精度和转台方位臂重力补偿精度有关。图9（c）显示转台方位臂倾覆力矩在不同条件下的大小，其精度在0.18%以内。如图9（d）所示，g条件下低重力补偿系统中全景相机转台方位关节、俯仰关节的转矩与1/6g条件下全景相机转台方位关节和俯仰关节的转矩，如图9（d）所示。其中，方位关节力矩由于吊丝系统的影响出现偏值，但整体转矩补偿精度在1%以内。

图9 仿真实验结果Fig.9 Simulation Results

5 总结

针对全景相机转台的结构特点提出了一种主动式吊丝配重方案。支撑吊丝、配重块的同步臂与转台相似，转台方位臂直接采用吊丝、滑轮和配重块进行重力补偿，转台俯仰臂采用了同步臂俯仰臂、转台俯仰臂和吊丝组成的平行四边形结构，简化了转台俯仰臂重力补偿的机械结构。该方案机械结构简单、控制方便。

然后对平行四边形机构进行了构型证明，并对全景相机转台低重力补偿装置控制误差引起的吊丝竖直偏角及重力补偿误差进行了理论分析。最后对该装置进行Adams动力学仿真。通过仿真分析，验证了平行四边形结构特点，转台俯仰关节转动时配重块上下无位移；同时验证了全景相机转台低重力补偿装能够实现转台低重力模拟。仿真结果为系统安装调试工作提供了理论基础。下一步将研究转台质量及质心测量，以及同步臂和转台同步运动的控制系统。