悟透本质 解题游刃有余——对一道三角形考题的多解探究

☉山东省肥城市第一高级中学 李康琦

本文拟通过一题多解的形式，着重探究：如何灵活运用所学知识、方法，灵活处理解三角形中的最小值问题，以帮助同学们厘清常用解题思维，进一步提高分析、解决此类问题的实际能力.

例 （2018年高考数学江苏卷第13题）在△ABC中，角A，B，C所对的边分别为a，b，c，∠ABC=120°，∠ABC的角平分线交AC于点D，且BD=1，则4a+c的最小值为______.

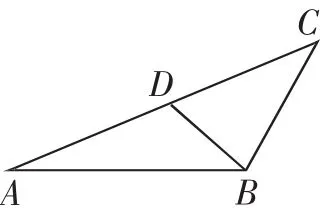
图1

解法一：如图1，结合题意画出图形，因为∠ABC的角平分线交AC于点D，所以，所以易知AD=

化简得a=c或a+c=ac.

当a=c时，易知a=2，c=2，所以4a+c=10.

综上，可得所求4a+c的最小值为9.

解法二：如图1，结合题意画出图形，因为∠ABC的角平分线交AC于点D，所以，所以易知=

故所求4a+c的最小值为9.

思路2：分解得（a-1）（c-1）=1，又易知a＞1，c＞1，所以4a+c=4（a-1）+（c-1）+5≥2

故所求4a+c的最小值为9.

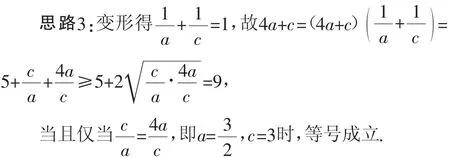
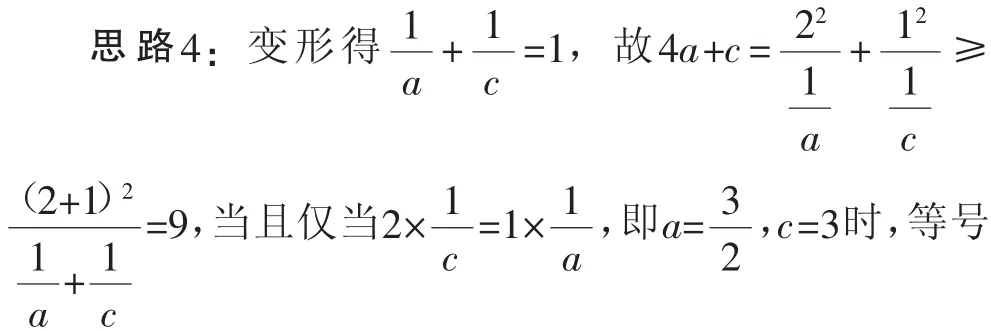
故所求4a+c的最小值为9.成立.故所求4a+c的最小值为9.

解法三：如图1，结合题意画出图形，因为∠ABC的角平分线交AC于点D，所以

解法四：如图1，结合题意画出图形，因为S△ABD+S△BCD=S△ABC，所以根据题设可得化简得ac=a+c.以下同解法二，略.

解法五：如图2，建立平面直角坐标系xBy，过点C作CE⊥x轴于点E，则易知点B（0，0），接下来，有两种不同的思路.

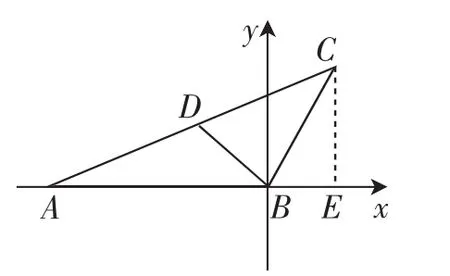
图2

以下同解法二，略.

以下同解法五思路1，略.

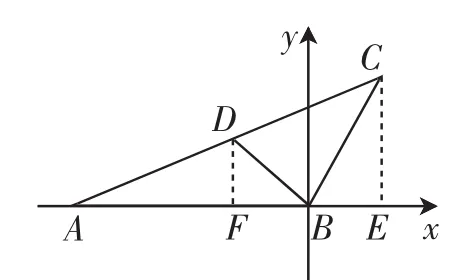
图3

解法六：如图3，建立平面直角坐标系xBy，过点D作DF⊥x轴于点F，过点C作CE⊥x轴于点E，则结合题设易知点A（-c，0），D）.于是，由A，D，C

三点共线得kAD=kAC，即，化简得a+c=ac.

以下同解法二，略.

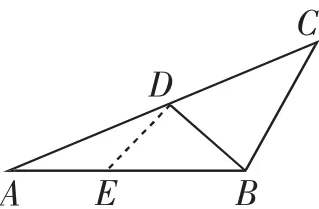
图4

解法七：如图4，过点D作BC的平行线，交AB于点E，则结合题意易知△BDE是边长为1的等边三角形.又根据DE∥BC 可得，即a+c=ac.以下同解法二，略.

评注：本题解法较多，求解关键是努力寻找三角形的边长a，c满足的关系式，可灵活利用解三角形中的正弦定理、余弦定理、面积公式加以分析；也可灵活利用有关平面向量知识加以分析；还可通过建系，充分利用相关点的坐标以及直线的方程、直线的斜率加以灵活分析；亦可灵活利用相关平面几何知识加以分析.显然该题可让不同的考生发挥各自的特长，故该题设计较好，值得我们细细品味、深思！

综上，从不同的思维切入，往往可获得不同的解题体验，真可谓“横看成岭侧成峰，远近高低各不同”，我们要在学中“悟”，在“悟”中不断提升解题技能.F