重问题内涵本质 促自然合理联想——对2018高考江苏卷第13题的探究与思考

☉江苏省清浦中学 吴洪生 时坤明

2018高考江苏卷第13题作为填空压轴题，其内涵丰富、解法灵活，对考生数学能力的要求比较高.在重视考查基础知识与通性通法的同时，着重考查学生对数学本质的理解，为引领高三复习教学起到了很好的导向作用.

一、试题呈现

在△ABC中，角A，B，C所对的边分别为a，b，c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为______.

二、命题分析

本题以三角形为载体，立足三角形内角平分线，将条件转化为三角形的两边a，c之间的关系，这样就对三角形面积、三角形内角平分线性质定理、定比分点坐标公式的向量表示形式、三点共线的充要条件等进行较为全面的考查.试题定位在填空压轴题，又将降元思想、二元变量最值求法、基本不等式等融入其中，意在提高问题的思维价值高度.试题形式简洁，内涵丰富，区分度较好，为数学思维水平高的考生留足了思维驰骋的空间.

三、题源探寻

本题背景中，A，D，C三点共线，有关三点共线的性质，在苏教版必修4第2.2.3节中有例4：在△OAB中，C为直线AB上一点

本题所求4a+c的最小值，在苏教版必修5有相似背景：第3章复习题13.已知正数x，y满足x+2y=1，求的最小值.

本题的高考原型有如下几个：

原型1（2010全国Ⅱ卷理科第8题）在△ABC中，点D在AB上，CD平分∠ACB.若=a，=b，|a|=1，|b|=2，则=（ ）.

原型2（2015全国Ⅱ卷文科第17题）在△ABC中，D是BC上的点，AD平分∠BAC，BD=2DC.

（2）若∠BAC=60°，求∠B.

原型3 （2012浙江卷文科第9题）若正数x，y满足x+3y=5xy，则3x+4y的最小值是（ ）.

原型4（2012苏北四市三模第17题）如图1，在C城周边已有两条公路l1，l2在点O处交汇，且它们的夹角为75°，已知OC=（+）km，OC与公路l1的夹角为45°.现规划在公路l1，l2上分别选择A，B两处为交汇点（异于点O）直接修建一条公路通过C城OA=xkm，OB=ykm.

图1

（1）求y关于x的函数解析式，并指出它的定义域；

（2）试确定点A，B的位置，使△OAB的面积最小.

四、解法探究

本题条件给出三角形内角平分线，这是解题的出发点与立足点；所求结论为4a+c的最小值，这是解题的归宿.基于此，本题需要分两步处理.第一步探寻a与c的关系：a+c=ac，这是解决问题的关键；第二步据此关系求最值.从不同的视角出发，第一步探寻a与c的关系有如下常见途径：①从条件与图形上看，首选面积法；②由三角形内角平分线的性质定理知，由定比分点坐标公式的向量形式或向量基本运算法则得两边平方或两边同乘B—→D均可得a+c=ac；③过D作DE∥BC交AB于E，则△BDE是边长为1的正三角形，由平行可得a+c=ac；④针对特殊角还可建系，既可以BD所在直线为x轴，也可以BA或BC所在直线为x轴，方法灵活.第二步由a+c=ac求4a+c的最值，常有如下途径：①将a+c=ac变形，用“1”的代换法；②将a+c=ac变形为代入4a+c，用降元法转化一元函数或构造基本不等式；③换元法，令t=4a+c，则c=t-4a，再代入a+c=ac，转化为关于a的二次方程，运用Δ≥0可得.

解法1：由等面积法得S△ABD+S△BDC=S△ABC，即sin120°，即a+c=ac，从而=1，

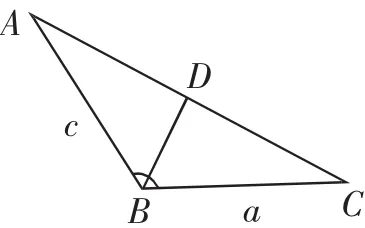
图2

图3

图4

解法4：建立如图4所示直角坐标系，则C（a，0），D（cos60°，sin60°），A（ccos120°，csin120°），

因为A，D，C三点共线，kAD=kDC，

五、变式拓展

变式1： 在△ABC中，A，B，C所对的边分别为a，b，c，已知∠ABC=120°，AC边上的中线BD=1，求a+c的最大值.

变式2：在△ABC中，A，B，C所对的边分别为a，b，c，已知∠ABC=120°，点D满足2，且BD=1，求a+c的最大值.

令a+c=t，把c=t-a代入（*）式用判别式法解决.

评注：2018江苏高考13题→变式1→变式2，观察点D的位置及比值的变化：将角平分线变为中线，再变为三等分点连线.不难发现问题的演变规律.

变式3：如图5，在△ABC中，A，B，C所对的边分别为a，b，c，已知∠ABC=135°，BD、BE三等分∠ABC，且BE=1，则2a+c的最小值为______.

图5

评注：变式3是将13题中的角平分线变为三等分角线，为方便运算将120°角改为135°角.

六、教学思考

本文选择2018高考江苏卷第13题，结合学生的认知情况、思维层次，运用一题多解、拓展变式的研究方法由表及里，由浅入深，对其进行了最大化的挖掘，力求做到以点窥面，全面提升学生的思维层次.通过对本题的探究，笔者有如下思考与感悟，简称为“四重视一追求”.

1.重视基础吃透本质

新《课标》指出：要让学生在数学学习中获得必要的数学基础知识和基本技能，理解基本的数学概念、数学结论的本质.在高三复习特别是一轮复习中要高度重视夯实基础，对于像三角形内角平分线性质定理这样的结论，尽管初高中教材均没提及或者说不作要求，但在各类考试中频频出现，应用十分广泛，如能合理使用，将会优化思路、简化运算，起到事半功倍的作用.因此，高三复习教学应引导学生重视基础、吃透本质，加强对数学本质的认识与理解，全面提高学生的数学思维能力.

2.重视运用通性通法

章建跃博士说：“通性”就是概念所反映的数学基本性质；“通法”就是概念所蕴含的数学思想方法.重视通性通法，就是要求学生在数学解题中养成从基本概念、基本原理出发，运用定理、公式等思考和解决问题的习惯，学会最基本的数学思考方法.例如：由4a+c的最小值，此类题有两种常见思考方法：

①已知a，b，m，n，λ，μ，k∈R+，m，n，λ，μ，k为常数，且先变形，展开后利用基本不等式求最小值.

②已知a，b，m，n，λ，μ，k∈R+，m，n，λ，μ，k为常数，且=k，求ma+nb的最小值.这里只需由ma+nb=（ma+展开后即可利用基本不等式求最小值.

3.重视多解多变训练

一题多解是指对同一问题从多个视角进行剖析、求解.如：本文对2018江苏高考第13题给出了四种解法，各种解法既有板块内的融合，也有自成一体.重视一题多解训练，有利于开阔学生的思路，融合相关的知识与方法；有利于学生对问题进行多角度思考、多层次分析，形成广阔的审题视角；有利于培养学生思维的发散性与灵活性.一题多变是指对一道题改变或部分改变其条件或结论，通过联想、类比得到一系列新的题目.如：本文变式拓展给出了三种变式，对知识进行了纵引横联，拓展引伸.重视一题多变训练有利于学生掌握数学知识及其内在的联系；有利于提升学生的思维能力和创新能力.

4.重视总结勤于反思

“学而不思则罔，思而不学则殆”.反思是师生对教学实践过程的再思考、再认识.重视总结与反思，有利于教师总结经验教训，进一步提高教学水平.有利于学生深化对知识的理解，提升思维能力；有利于改进方法，提高学习效率；养成对自己解题过程进行回顾和反思的习惯，有利于总结解题经验、提炼解题方法、揭示数学思想，形成正确的解题观.

5.追求自然合理联想

对于数学问题的解决，学生常出现一听就懂、一过就忘、一做就错的现象.为什么会这样？部分原因在于学生对问题解决方法的自然合理性没有真正认识和把握，使得知识不能迁移.如何才能让学生有自然合理的联想呢？本文作了有益的尝试.如：本题条件中给出了三角形的一条内角平分线，内角平分线（或中线或高）将三角形分割成两个小三角形，联想面积法自然合理.其次，由三角形内角平分线，联想三角形内角平分线的性质当属知识的自然迁移.再次，由A，D，C三点共线，联想定比分点坐标公式的向量形式，进而将B—→D用B—→A，B—→C线性表示，也符合学生的认知结构，当然本题条件与结论中均未出现向量，让学生联想向量也是富有挑战性的.也还可以从平几知识出发，添置平行线得比例关系，进而有ac=a+c也符合学生的认知.得到ac=a+c后，求4a+c最小值，这属于二元变量最值问题常见题型，在高考及各地模考中屡见不鲜，解法灵活多变.这样的思维过程自然顺畅，一气呵成！