如何利用有效变式培养学生的探究意识与能力

☉江苏省张家港市沙洲中学 戴御梅

对某个数学问题进行有目的、有计划的变形并因此将学生引领进新的数学问题中进行思考与探究的教学就是我们数学教学中经常提及的变式教学.变式教学这一教学手段虽然在数学教学中得到了很广泛的运用，但变式的有效性却不是每位教师在教学中都能够保证的.事实上，教师在教学中应首先考虑学生思维的最近发展区，并引导学生从“变”的现象中探寻“不变”的问题本质，并继续探求出其中“变”的规律并因此充分调动学生的探究热情，使得学生能够在积极的思考中获得数学能力与思维水平的双方面发展.笔者在“向量”的复习教学中曾经着眼于一个比较简单的问题，引导学生对其进行了有效的变式与探究，效果很好.

一、问题的提出

图1

设计意图：一个简单的问题将作图方法、基本知识、解题技巧都进行了较好的复习，而且还为后续的变式研究打下很好的基础.

二、系数简单变式

设计意图：三角形排列顺序使面积比跟条件等式中的顺序保持一致是笔者有意而为之，这一更加贴近学生最近发展区的安排能够有效促进学生思考.

图2

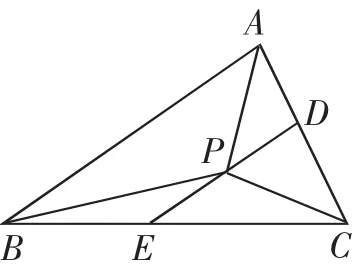
图3

师：通过条件等式的转化及平行四边形的法则作图使得P点位置得以确定.确定P点位置是否可以与引例联系呢？

生4：构造三角形并使点P成为三角形的重心之后借助引例的结论来解决.

如图4，延长PB至点B，使

图4

1PB1=2PB，延长PC至点C1，使PC1=3PC，连接AB1、AC1，所以，由引例，P是△ABC的重心，所以S=

11△PAB1

S△PAC1=S△PB1C1，易得S，所以

△PAC1

师：我们都知道平行四边形法则、三角形法则是解决向量和差这一类问题的重要方法，还有其他方法吗？

生5：坐标运算法也可用，我觉得取特例正三角形ABC是可行的.

笔者及时进行了鼓励并引导学生探寻解题思路.

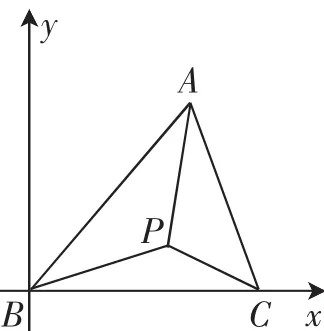
图5

师生共同运用从特殊到一般的解题思路进行了探究，如图5，由两边向量纵坐标相等得（yA-yP）+2（yB-yP）+3（yC-yP）=0，所以yA=6yp，所以

师：太棒了！

笔者引导学生对此题所运用的所有解法进行了总结与对比，对于学生能够积极思考并将类比、转化等思想方法运用得如此游刃有余进行了及时的表扬和肯定，学生从数的角度、形的角度对同一个问题进行了不同的思考.此时有学生发现了题中最后求得的面积比正好是已知等式中系数的比这一现象，笔者没有进行简单的否定或忽略，而是将学生的这一发现当成了训练学生推理能力的契机，于是让学生进行了验证猜想的引导并获得了意外的收获.

生6：我换了三个系数进行了计算，发现面积的比刚好都是已知等式中系数的比，这是巧合吗？还是本来就存在这样的规律呢？

学生很快投入到自己的思考及演算中去了.

三、探寻问题本质规律

师：当真会有如此奇妙的规律吗？大家首先自己探讨一下.要想使面积之比与已知等式中系数之比相等就必须满足系数符号均为同号这一条件.接下来让我们以正数来验证这一规律吧.

生7：经过验证能发现这一规律在一般情况下一样成立.

大多学生运用变式1的第三种方法对此规律进行了验证，验证的成功使得学生都很兴奋，对于变式与拓展的探究热情更加高涨，笔者乘势抛出了进一步拓展的问题：

学生在一定的方法比较之后选择了坐标法进行解题，则△PBC、△ABC的面积之比等于P、A纵坐标的绝对值之比，则S1∶S2∶S3等于|m|∶|n|∶|p|.

全班响起了热烈的掌声.

四、探求“形似”问题的本质区别

设计意图：引导学生从形似问题的解决中认识到简单套用结论做题是比较片面的做法，解题时应搞清楚条件与结论的对应关系并运用好转化与处理问题的方法，使学生能够在这种类似题目中进一步提炼解题的思想方法.

有学生在这两个变式练习中感觉困难，教师可以加以适当的点拨来帮助学生突破难点、总结解题规律和注意点.

生8：等式左边的三个向量都是将非三角形的顶点作为起点的，而等式右边又是零向量，小三角形面积比的系数对应着所给等式左边中不在小三角形中的向量系数，比如变式1中△PBC缺少A，因此面积之比中和它对应的就是P—

→A的系数.师：这个结论很好，不过进一步了解数形结合、从特殊到一般、猜想与验证等思想方法在今后学习中的作用才是更加重要的，大家在课后再考虑一下，这个结论反过来是否成立.

设计意图：这一设计对于学生思维的纵深发展是尤为有意义的，学生在这样的变式中进一步拓展了思维的空间及辩证看待问题的意识.

贴近学生最近发展区设计的有效变式能够使学生的好奇心在这些拓展性练习中更加强烈，探究知识的愿望转化成了学生内心的强烈需求，学生思维的活力、探究的主动性也因此得以更好地展现.

教师设计有效变式进行教学时应有意识地为学生创造更加广博的思考与探究空间，引导学生养成从各种不同角度观察问题、思考问题的意识和习惯，使学生能够在解题时有意识地探究更多不同的解题思路与方法，在条件的增删、变化中拓展数学问题并探究一般规律，使学生的思维空间与学科素养都在问题变式的探究与解决中不断得到拓展.F