基于数学模型的“微专题”设计——以不等式模型≤ln(x+1)≤x为例
2018-09-15江苏省常熟市中学
☉江苏省常熟市中学 宗 蕾
相对于综合性强、覆盖面广的“大专题”教学而言,微专题教学具有“因微而准、因微而细、因微而深”的优势.微专题教学把知识难点分解成一个个独立的问题集,从而在课堂教学中帮助学生集中火力突破难点、拓展思维,能起到“见微知著”.促进学生深度学习的效果.正如教学设计是决定课堂教学成效的关键因素,“微专题”的设计也决定了微专题教学的成败.“微专题”设计是指教师针对某一具体知识点、能力点、易错点或检测点,从其涉及的基本概念、基本原理或基本方法入手,精选例题和习题,编制、设计成能够在一定课时内完成的专题(教学任务).有效的微专题设计,离不开一定的数学模型.可以说,微专题的设计就是数学模型的选择到数学模型的分析、应用、拓展的过程.因此,微专题的设计一般需要遵循以下几个步骤.
一、选择适合的数学模型
数学模型是利用数学语言模拟现实的模型,即把某种事物的主要特征和关系抽象出来,用数学语言概括的一种数学结构.G·波利亚指出:“良好的组织结构使得所提供的知识容易应用,这甚至可能比知识更为重要.”数学模型就是结构化的知识,指引着问题解决的路径.可以说,缺少数学模型这一“中间环节”,数学试题与解题目标就会隔着难以逾越的障碍.在微专题的设计中,首要就是选择适合的数学模型,选择的数学模型需要符合四个特征:工具性、适应性、可变化性、可延展性.
例1 (2018年浙江第10题)已知a1,a2,a3,a4成等比数列,且a1+a2+a3+a4=ln(a1+a2+a3),若a1>1,则( ).
A.a1<a3,a2<a4B.a1>a3,a2<a4
C.a1<a3,a2>a4D.a1>a3,a2>a4
该题需要设公比为q,由a1-a3=a1(1-q2),a2-a4=a1q(1-q2),不难看出,此题就是判断公比q的取值范围,其中选项A对应q∈(1,+∞),选项B对应q∈(-1,0),选项C对应q∈(-∞,-1),选项D对应q∈(0,1),由此可见,解决本题的关键是转化为一个关于公比q的方程,并判断其解的范围.
解析:由a1+a2+a3+a4=ln(a1+a2+a3)≤a1+a2+a3-1(不等式放缩依据:lnx≤x-1),得a4≤-1,可得公比q<0.
若q≤-1,则a1+a2+a3+a4=a1(1+q+q2+q3)=a1(1+q)(1+q2)≤0,而ln(a1+a2+a3)=ln[a1(1+q+q2)]≥lna1>0,矛盾.
故有q∈(-1,0),选B.
例2(2018年全国卷Ⅲ理第21题)已知函数f(x)=(2+x+ax2)ln(1+x)-2x.若a=0,证明:当-1<x<0时,f(x)<0;当x>0时,f(x)>0.
又f′(0)=0,得f(x)单调性,从而得证.
上述不等式模型就是经过高度抽象后的结构化知识,基于不等式模型的重要地位,可以此为核心进行微专题设计.通过对不等式模型及典型问题的分析,总结出一般的规律、方法或者技巧,优化学生的知识结构,强化学生的思维方法,提升学生的解题能力,从而提高学生的数学学科素养.
二、追溯数学模型的本源
每个数学模型都有其来源.带来学生深入挖掘数学模型的来源,是“微专题”设计的重要环节.追溯数学模型的本源,利于提高学生的学习兴趣,培育学生科学精神和探究意识,特别是学生从数学模型的形成过程中掌握了其背后蕴含的数学原理,这是学生深度学习的重要基础.带领学生追溯数学模型的本源也利于培养学生形成“从已有经验出发,将实际问题抽象为数学模型并进行解释与应用,进而获得数学理解”的模型思想.在“微专题”设计中呈现数学模型的本源探究,可以突出三个方面:
1.追溯数学模型的原型
2.模拟数学模型形成情境
模拟呈现数学模型形成时的情境,可以使学生“代入”到相应的境域,形成“专家型”的思考,从而“发现”知识和规律.在这里,教师设计有梯度的问题是关键.
问题1:假设小明在银行里存1块钱,银行的年利率是100%.
(1)请问一年后,“本金+利息”小明共能得到多少钱?
(2)若小明1块钱存半年,取出再存进去,一年后小明能得到多少钱?
(3)若小明1块钱每1个月存取一次,一年后小明能得到多少钱?
(4)若小明1块钱每天存取一次,一年后小明能得到多少钱?
意图:通过此问题了解“复利”的概念,通过运算引导学生发现复利的变化规律:本利和的多寡,由计息周期而定,以一年来说,可以一年只计息一次,也可以每半年计息一次,或者一季一次,一月一次,甚至一天一次.当然计息周期愈短,本利和就会愈高.
问题2:如果计息周期无限制地缩短,比如说每分钟计息一次,甚至每秒,或者每一瞬间(理论上来说),会发生什么状况?本利和会无限制地加大吗?
意图:通过计算器验证,发现最后的本利和趋向于2.718 28……于是得到一般化的结论
3.推导数学模型的结论
让学生尝试推导出数学模型,学生在得到结论的同时能够获得巨大的成就感,不仅初步获得了数学建模的方法,更重要的是通过数学的方法获得了新知,打开了一扇通往广阔世界的大门.
构造函数f(x)=ln(x+1)-x,利用导数容易得到ln(x+1)-x≤0恒成立,即ln(1+x)≤x成立.
在ln(1+x)≤x的基础上,把x用x-1代入,得到lnx≤x-1,把x用代入,得到ln,经过变形得到,再把x用x+1代入,于是就得到
三、模型应用及变式技巧
数学模型是为解决数学问题服务的.在“微专题”设计中,教师需要立足学生的经验背景、知识水平、理解程度,立足知识之间的联系设计数学模型的应用例题,让学生在例题的思考与解答中体会模型的应用方法与应用技巧,加深对数学模型的理解.首先,设计的例题要具有代表性,能够直接体现数学模型应用的一般规则.其次,例题要具有层次性,由易到难,由一般应用到复杂应用逐层展开.再次,例题需要体现一定的认知冲突性,利用学生思维与例题要求的差异,碰撞出思维的火花,在认知冲突中加深反思,明了方向.
例4已知函数f(x)=alnx-ax-3(a≠0).
(1)讨论f(x)的单调性;
(2)若f(x)+(a+1)x+4-e≤0对任意x∈[e,e2]恒成立,求实数a的取值范围(e为自然常数);
(3)求证:ln(22+1)+ln(32+1)+ln(42+1)+…+ln(n2+1)<1+2lnn!(n≥2,n∈N*).
解析:(1)(2)略.
(3)证明:由(1)知,f(x)=-lnx+x-3在(1,+∞)上单调递增,所以当x∈(1,+∞)时f(x)>f(1),
即-lnx+x-1>0,所以lnx<x-1对一切x∈(1,+∞)成立.
因为n≥2,n∈N*,
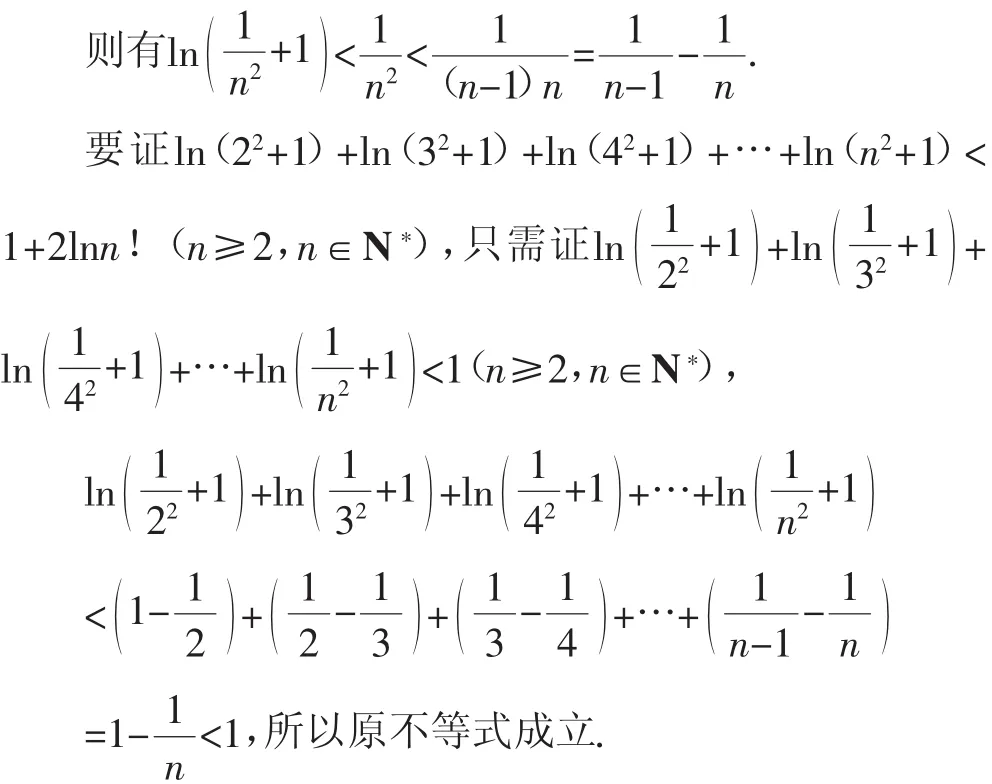
本题是数学模型应用的较高层次,同时又有一定的变化,与学生原有思维间存在着一定的认知冲突.学生要先利用行裂项.教师通过此例题可以更好地发展学生灵活运用数学模型的能力.
四、数学模型的延伸研究
对数学模型的理解和应用不应闭门造车,教师应该充分发挥数学模型“知识联系桥梁”的特性进行适度地拓展延伸.对数学模型除了溯源之外,还需“登高”.教师对数学模型的延伸研究也是教师的一个再发现、再创造的过程.在“微专题”设计中,教师通过对数学模型的深入研究,深刻把握问题的实质,不断拓展数学模型的外延,使学生对数学知识的本质有着更深刻的理解,达到触类旁通、触碰问题本质的目的,从而扫除解决问题的障碍.
例5 (2017年浙江第22题)已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(n∈N*).证明:当n∈N*时,
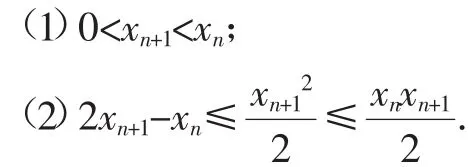
证明:(1)略.

总之,从系统思想的角度看,“微专题”是“大专题”的一个有机补充,在促进学生深度理解数学知识、提升解题能力、培养数学素养方面起着重要的作用.通过科学选择数学模型、追溯数学模型的本真、应用拓展数学模型,提升“微专题”设计的整体水平,从而促进学生对基础知识的复习巩固,促进学生基本技能的提升,帮助学生建立起系统的认知,强化学生深度学习的能力.
