初中数学等差数列问题的有效教学探究

◆闫岚子

等差数列是高中阶段数学学习的重要内容，然而等差数列常以探索型问题提前出现在初中阶段，表现为给出一列数、一列等式、一列图形的前几项，要求通过观察、分析、归纳、总结、猜想等方式推出一般性的结论；或是给出一个图形，要求学生探索图形成立的条件及其变化规律。教师在讲授这类问题时既不能像对待高中生那样用严密的逻辑推理导出通项公式和求和公式，更不能直接给出公式让学生死记硬背应付考试，也不能放任肆意猜想，思维散而难收，学生即使偶尔做对题目，也有碰运气的成分在里面。如何就此问题做到有效教学，乃至学生做到高效学习，是每个数学教师思考的问题。下面，笔者根据多年来的教学经验，就有效解决这类问题作一个初步的探究。

1 等差数列变化规律的分析与总结

虽然初中阶段还没有正式学习数列，但代数式意义、字母表示数、代数式表示简单数量关系，学生已经学习掌握并能熟练应用。用含n的代数式表示数列第n项是探究数列变化规律的目的也是手段。

1.1 等差数列的第n项的表示

一列数中，前后相邻两项数的差都相等的数列叫等差数列

以下是常见的等差数列(n为正整数，也是序数)

自然数：1,2,3,4,…n

偶数：2,4,6,8,…2n

奇数：1,3,5,7,…2n-1

3的倍数:3,6，9， …3n

相差3的数:4，7，10，...

=3×1+1，3×2+1,3×3+1，…3n+1

通过观察发现：

自然数是相差1的等差数列，相差1的等差数列第n项是n

偶数和奇数都是相差2的等差数列,相差2的等差数列第n项含2n

相差3的等差数列的第n项是含3n

【归纳】等差数列相差的数与用n表示的第n项有一定的关系，相差多少就是多少n，即相差k就是kn；再令n=1让含n的代数式值等于数列的第一个数即首数，从而确定出用含n的代数式表示的第n项。

例：4,6,8,10,… 相差2就是2n令n=1,2n+2=4，则2n+2是该数列的第n项。

5,11,17 ,… 相差 6就是 6n令n=1,6n-1=5,则6n-1是该数列的第n项,并验证正确。

由此可以容易得：

（1）相差1的数列

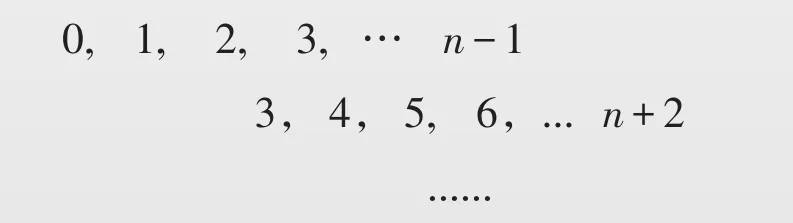
（2）相差2的数列

（3）相差3的数列

相差k就是kn，即第n项是kn±b

1.2 等差数列的应用

1.2.1 探索结论成立的条件

观察上面一列算式，你发现其中规律，用含n的代数式表示这个规律。

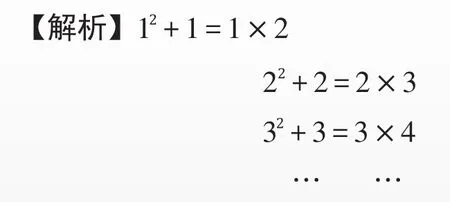
第n行n2+n=n×(n+1)

答案：n2+n=n(n+1)

1.2.2 探索图形变化规律

探索图形变化规律：从图形的生成入手，需要靠想象，让第一图和第二个图形重叠，多余出来部分就是增加的数，依次把第二个图形和第三个图形重叠；除了靠想象外，也可以用笔涂出前面的图形，没有涂过的为多余部分，再看每次多余出来的部分是否完全一样，如果一样，即为等差数列，快速写出第n项；如果不一样，可以观察每次多余出数的特点，再根据特点找出规律，列出第n项。也可以从数字特点上出发，找出规律。

(1)(2008·湛江)为了庆祝“六·一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛如图所示：

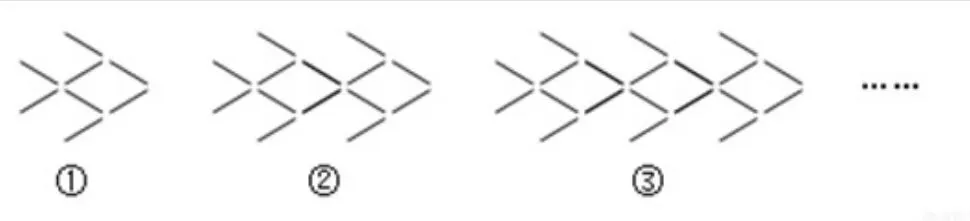
按照上面的规律，摆n个“金鱼”需要火柴的根数为（）

A．4+4nB.8+6nC.2+6nD.8n

【解析】想象图1和图2重叠，图2和图3重叠，多余部分都是,即图形依次多出6个火柴棒，为相差6的等差数列，第一个图的根数是8，即首项是8。多6为6n当n=1时6n+2=8第n个图形的根数为6n+2

答案：C

（2）（海南省中考）用同样黑色棋子按如图所示的方式摆放，按照这样的规律摆下去，则第n个图形需要棋子________枚(用含n的代数式表示)

【解析】把前面图和后面的图重合，均多出,即多3，第1个图有4枚棋子即首项是4，多3就是3n,当n=1时，3n+1=4，所以第n个图形有3n+1枚棋子

答案：3n+1

(3)下列是同型号黑白两种颜色的正三角形瓷砖按一定规律铺设的图形。仔细观察图形完成图④并写出第n个图形有多少块黑色的瓷砖（用含n的代数式表示）

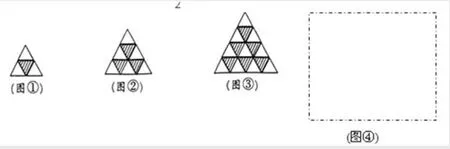
【分析】用重叠或涂抹得出的多余部分均不一样，依次多余出的数为2,3,4…。从图形的生成特点上观察出：第1个图1

第2个图1+2

第3个图1+2+3

……

第n个图1+2+3+…+n

而1+2+3+…+n为等差数列的和，如何计算等差数列的和是我们下面要解决的问题

2 探究等差数列的求和公式

2.1 三角形数1+2+3+4+…+n=?

数学家高斯在读小学二年级时，老师出了这样一道计算题

1+2+3 +…+100=?

高斯很快得出了答案，他的计算方法是：

古希腊毕达哥拉斯学派认为“万物皆数”，意思是数是宇宙万物的要素，他们常把数描绘成沙滩上的点子或小石子，根据点子或小石子的排列的形状把整数进行分类。 13610…这些数叫三角形数如图示

应用已知一列数：1，-2，3,-4,5,-6，7,…将这列数排成下列形式

按照上述规律排下去，那么第10行从左边数第5个数是________。

【解析】通过观察发现：数列偶数为负，奇数为正，每行末尾数的绝对值为三角形数

计算第10行的上一行第9行末尾数绝对值为:

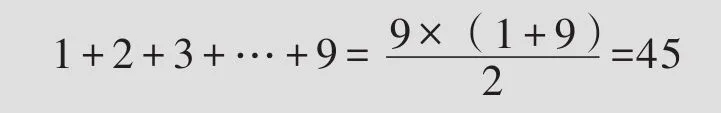
则第10行左数5个数为-50

2.2 三角形数1+2+3+4+…+n=

（1）2+4+6+8+…+2n=?

由：2+4+6+8+10+12+14 (n=7)

应用1找规律

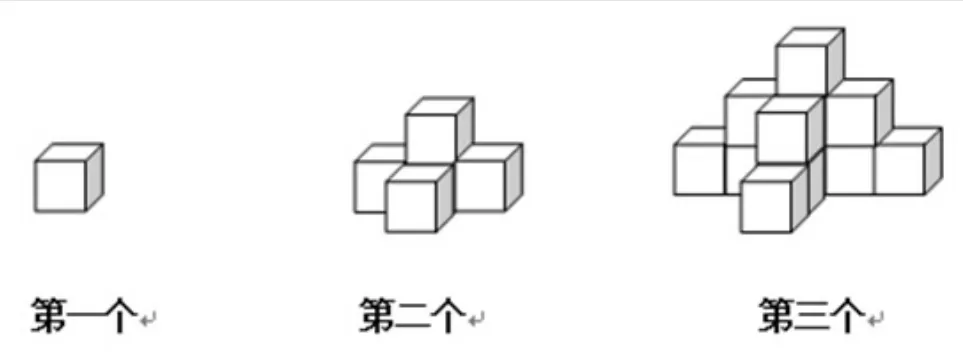
（1）如图，第1个中有几个正方体？第2个中有几个正方体？第3个中呢？

（2）照图示的方法摆下去，第5个中有几个正方形？第10个中有几个正方形？第n个呢？

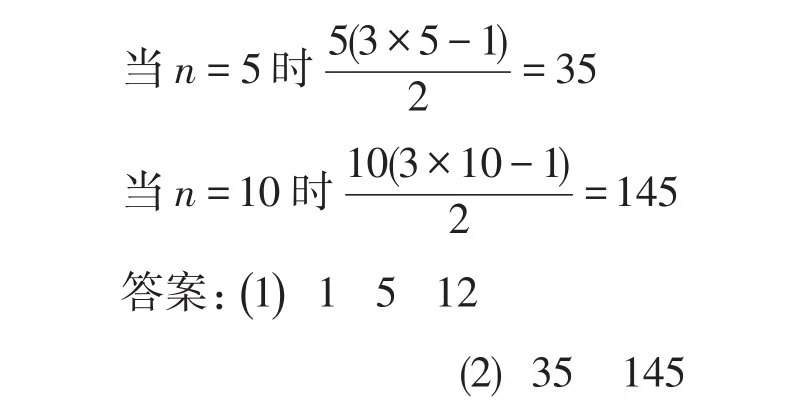
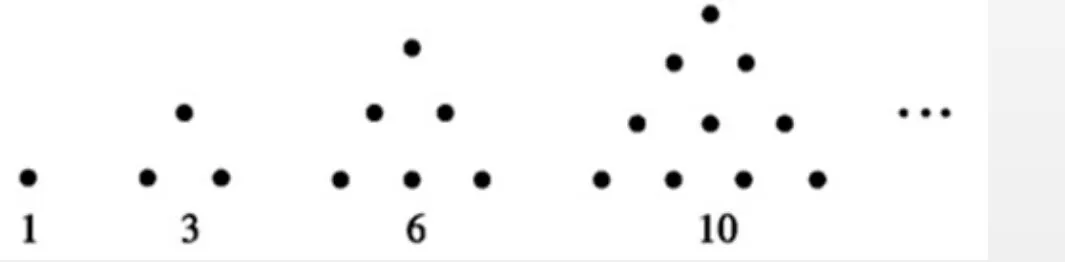
2根据下列5个图形及相应点的点数的变化规律，试写出第10个图中有________个点，并猜测第n个图形有_______________个点。

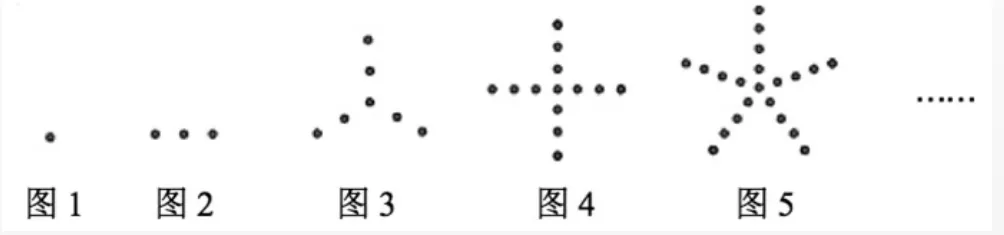
【解析】图1：1+0

总之，在求解规律问题时，应有效引导学生认真观察，合理推理，培养学生观察、分析、归纳、总结、猜想、类比等数学思想，并由此获得探索问题的一般方法和技巧，从而使学生达到高效学习。