从抽象到具体：例谈高中物理复习课教学设计——以“一动一静碰撞模型的研究”复习课为例

刘祖鸿

（寿宁县第一中学，福建 寿宁 35550 0）

复习课常常会陷入通过大量的解题训练来提高解题熟练度和解题技巧的误区，而忽视复习教学中从物理本质规律出发深入探寻物理现象或物理问题形成的根本原理，从而造成部分学生在解决实际物理问题时重计算轻分析，知其然而不知其所以然，对所得到的结论也缺乏有效的论证途径，这种复习方式明显与培养学生学科核心素养的要求是不相适应的。马克思认为：“人的认知过程需经历由感性认识到思维的抽象再上升到思维的具体的过程。”从抽象上升到具体是一个完整的思维过程，它包括起点、中介和终点三个基本环节。与新授课的重点是“理解知识产生过程”相比，复习课就是要把平时相对独立的知识，以再现、整理、归纳的方式串联起来，进而使学生加深对知识的理解，发现知识间的逻辑关系，提升分析问题和解决问题的能力。［1］为此，在《一动一静碰撞模型的研究》复习课教学中，教师设计了从抽象到具体的五个层层递进的问题：以“问题一”引入新课，使学生回忆起在新授课阶段学生在已有认知的基础上从生活场景、实验现象中已抽象提炼出的概念、规律、方法，并以此作为思维上升的起点；以“问题二、问题三、问题四”为中介，通过数学计算、结论讨论、探究本质，促进学生知识方法体系的建立与提升；以“问题五”为终点，通过建模迁移应用，优化知识方法体系，培养学生解决实际问题的能力。

一、整理知识碎片

相对于新授课而言，复习课容量“大”、内容“旧”，对于部分学生而言，复习课前知识“碎”、方法“散”、思维“乱”、课堂“乏味”为激发学生兴趣，借“旧”引“新”，在课题引入阶段，教师设计“问题一”直奔主题。

问题一：如图1所示，在光滑水平面上，质量为m1=300g的小球A以速度v0=10m/s与处于静止状态的质量为m2=200g的小球B发生对心正碰，碰后A、B两个小球的速度v1、v2的可能值为

A．v1=8m/s、v2=3m/s

B．v1=5m/s、v2=8m/s

C．v1=4m/s、v2=9m/s

D．v1=-2m/s、v2=18m/s

研究方法一：选项排除法

1.碰后不穿越，即v1≤v2可排除A；

2.动量要守恒，即m1v0=m1v1+m2v2，可排除B；

图1

本节课为高三物理一轮复习中《动量》模块中的知识应用课，教师以提出问题的方式引入课题，因为此类题型学生在高二时已有做过训练，学生较为熟悉，但由于间隔时间较久，大部分学生对原有知识已有所遗忘或碎片化，问题以选择题方式呈现，旨在引导学生在解决问题的过程中唤醒记忆碎片，提炼解题方法，实现知识结构的初步系统化。

在教学实践中，绝大部分学生均采用“选项排除法”，逐渐回忆出一维碰撞问题要遵循“碰后不穿越、动量要守恒、动能不增加”的解题依据，在对选项逐一分析中初步明确碰撞中两物体的速度关系、动量关系与能量关系，初步对已掌握的知识进行了梳理，掌握解决此类问题的简单方法。

二、建立方法体系

应用“排除法”虽然能解决以选择题方式呈现的“问题一”，但学生对碰撞规律的掌握是片面的，对物理原理的理解是肤浅的，对物理思想方法的应用是缺乏系统性的，为此，教师对问题进行了升级改造。

问题二：如图所示，在光滑水平面上，质量为m1=300g的小球A以速度v0=10m/s与处于静止状态的质量为m2=200g的小球B发生对心正碰，求碰后A、B两小球的速度v1、v2的取值范围。

研究方法二：列式计算法

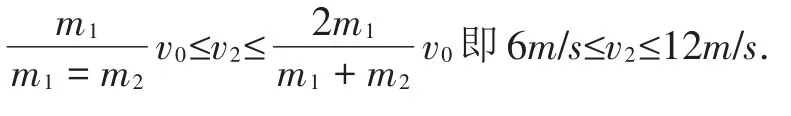
与“问题一”的条件完全相同，虽然教师只是对问题呈现方式进行了简单改造，但却“逼迫”学生不得不舍弃简单的“排除法”，转而对问题进行深度分析，在列式过程中进一步对知识进行系统性梳理，在解不等式的过程中训练了应用数学方法解决物理问题的能力，促进学生应用物理方法和数学方法相结合解决问题的常规方法体系建立。

三、巩固思想方法

随着“问题二”的解决，表面上看，学生似乎对一动一静碰撞问题有了较为全面而系统的认识，但从实质上看，学生通过列式计算所得到的结论，更多地是停留在从数学视角来分析问题，而从物理学视角分析客观事物的本质属性、内在规律及相互关系是存在明显不足的，为此教师需要引导学生从物理学视角通过交流、讨论的方式对上述结论进行充分地科学评估、论证和推理。

问题三：讨论上述解法中“等式”的物理意义

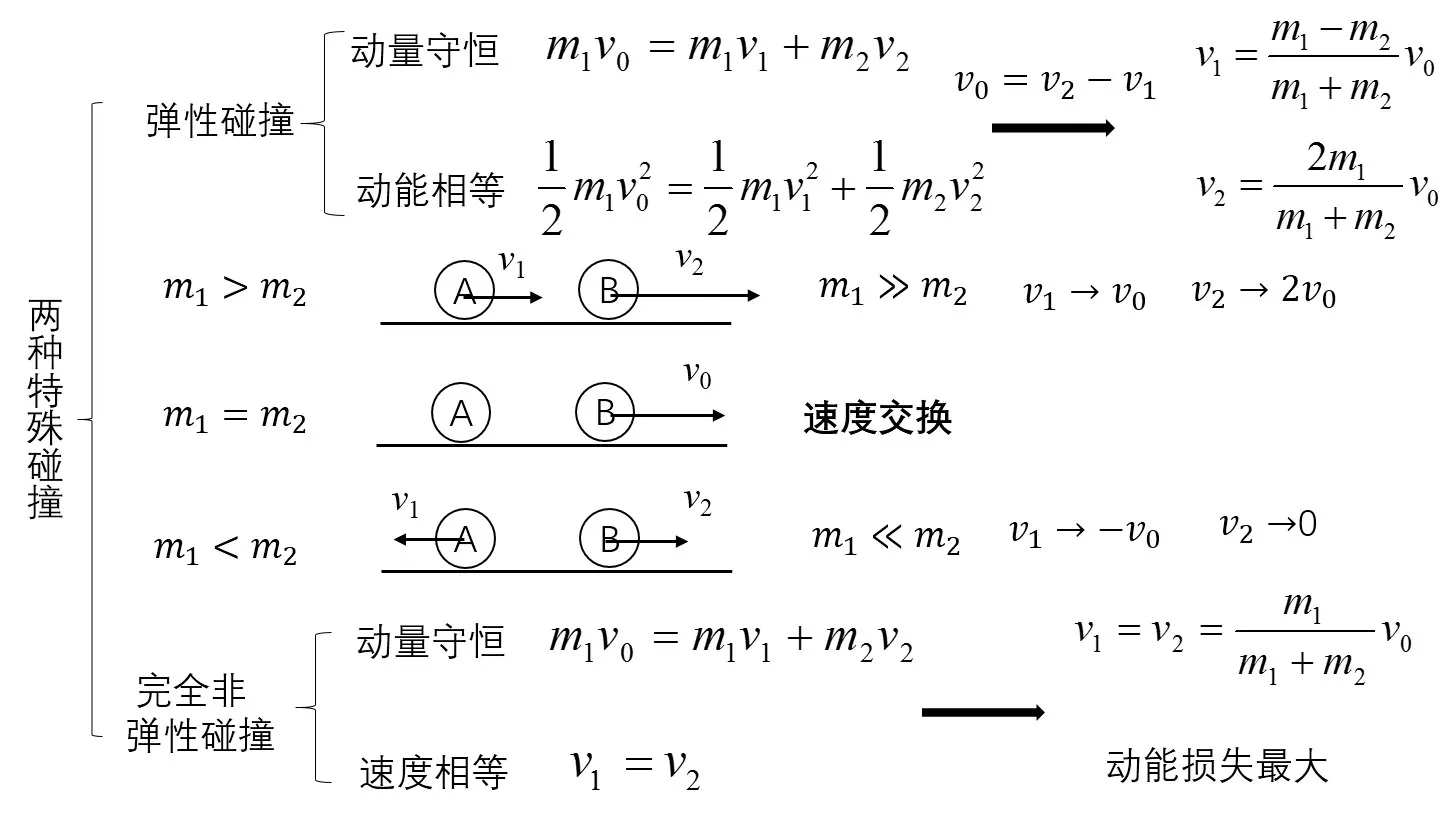
研究方法三：特例分析法

在已有结论的基础上，教师进一步引导学生对结论中的等号进行分析，从一般到特殊，再从特殊回到一般，使学生从更高更全面的视角对两种特殊的碰撞问题进行重构（所得结论如图2）。

1.通过自主分析得到：当v1=v2时，两小球发生完全非弹性碰撞，此情况系统动能损失最大。

3.引导学生分析得到结论：在一维碰撞中两球碰后的相对速度总是不大于碰前的相对速度。提示学生“回头看”，用该结论再次解决“问题一”。

在对结论进行发散讨论的过程中，学生经历了“物理→数学→物理”的思维过程，进一步内化了分析综合、推理论证的思维方法，有助于促进学生物理观念形成和科学思维建立。

四、回归规律本源

应用动量、能量观点是解决碰撞问题的基本方法，但这种方法更侧重于对物质运动的始末关系的研究，而对物质间相互作用本质成因探讨不够，对学生物理观念的形成和科学思维的训练也是不全面的，因此，教师设计“问题四”要求学生从动力学角度对碰撞问题进行更为深入地研究。

问题四：从动力学角度分析两球碰撞过程的速度变化，研究两球碰后的速度范围

研究方法四：过程放大法

任务一：设两球发生弹性碰撞，画出碰撞过程的v-t图像（图3）

任务二：设两球发生非弹性碰撞，分析两球碰撞结束的可能时刻

任务三：分析两球碰后的速度范围

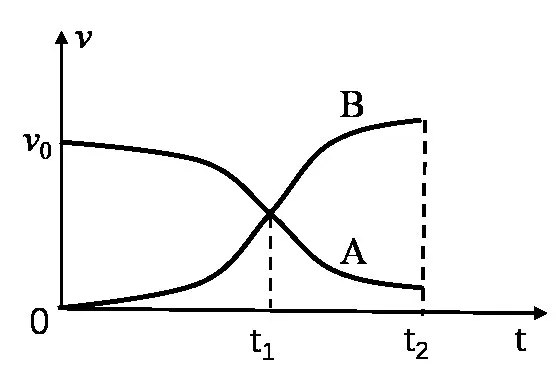
图3

为降低思维梯度，教师通过任务驱动方式对学生进行引导；为使物理过程形象化，教师通过教具（两个气排球）模拟碰撞过程中的不同形变；为实现思维可视化，教师通过弹簧模型对碰撞过程进行放大并类比分析。通过分析可知，A球在弹性碰撞过程先做加速度增大的减速运动后做加速度减小的减速运动（甚至可能反向加速），B球先做加速度增大的加速运动后做加速度减小的加速度运动，若为非弹性碰撞，在两球速度达到相等之前，由于A球速度大于B球，表示碰撞并未结束，故碰撞结束时间只能发生在t1～t2之间，其中若在t1时刻碰撞完成，则此时A、B球形变量最大，动能损失最大，为完全非弹性碰撞，若在t2时刻碰撞完成，则A、B球的形变完全恢复，可得碰撞前后总动能相等为弹性碰撞，在这个时间段内，从图像中很容易得出A、B碰后的速度介于完全非弹性碰撞和弹性碰撞之间。

在解决“问题二”和“问题三”的过程中，对数学思维要求较高，学生往往会陷入复杂的数学计算，对所得的结论也只限于是数学运算的结果而不识其实质物理成因，究其原因在于上述解法缺乏更为具体化过程性分析。“问题四”的提出，旨在通过动力学分析弥补仅从动量和能量角度分析造成的物理过程分析的缺失，使学生从本质上对碰撞问题能有更为全面、清晰、完整的理解和认识，既让学生掌握多视角分析解决问题的方法，也更容易让学生实现更高层次的知识系统化，进一步提高解决物理问题的能力。

五、迁移拓展应用

“碰撞”模型是高中物理的一个典型模型，能应用动力学、动量、能量观点综合分析碰撞问题的基本原理和本质规律只是实现本课教学的基本目标，复习课教学的根本目的是在探寻“现象本质”的过程中提炼出“方法本质”并迁移应用于解决更多更为复杂的问题。因此，教师需要对问题进行合理拓展，在对相似问题的处理中实现知识体系的深度融合和方法体系的迁移应用。

（1）小球冲上小车后能上升的最大高度。

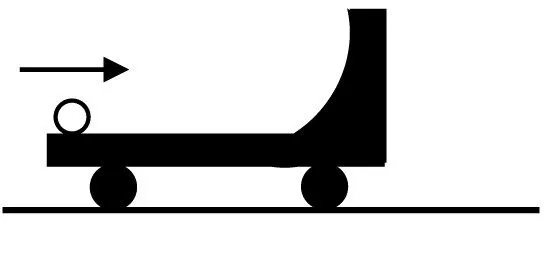
图4

（2）小球落地时距小车左端的距离。

研究方法五：类比分析法

“问题五”并非传统意义上的碰撞问题，教师在学生通过动力学、动量、能量多角度分析后引导学生与碰撞问题进行类比，会发现当小车运动到最高点时，与小车具有相同的水平速度，此过程类比于两小球的完全非弹性碰撞；当小球回到小车左端时，始末相比较，此过程类比于两小球的弹性碰撞模型。如图5，教师进一步展示物块弹簧模型、物块木板模型、子弹木块模型等，通过类比分析拓展，探寻各模型间的共性与差异，实现方法迁移，促进知识方法体系的深度融合。

图5

表面上看，高三复习课是为了应对高考所做的准备，实际上，复习课更承载着优化知识结构，建立内容更丰富、联系更紧密、层次更立体、方式更多样的知识体系和方法体系的功能。［2］通过合理地设置问题情境，引导学生由浅入深、由易到难、由抽象到具体应用多种方法从多维视角解释现象探寻本质，让学生在温故中而能知新。通过复习，让学生记住几个结论并不难，但通过刻板记忆得来的结论痕迹必将随着时间推移在学生头脑中逐渐淡化，而如果能让学生在学习过程中积淀下研究物理问题的思想方法，在解决实际问题的过程中培养学科的关键能力，即便日后学生忘了某些物理结论，但通过科学推理仍能还原现象本质，这样的物理教学才是真正有效和有价值的。［3］