摆动转子压缩机转子系统模态分析

周盛杰 潘树林 李 伟 饶金强



摆动转子压缩机转子系统模态分析

周盛杰 潘树林 李 伟 饶金强

（广西大学广西石化资源加工及过程强化技术重点实验室 南宁 530004）

运用SolidWorks软件建立了摆动转子压缩机的偏心轮轴及电机转子等所组成的转子系统的动力学模型，并利用ANSYS Workbench软件对转子系统进行模态分析，得到其各阶固有频率和振型。分析结果显示现有的摆动转子压缩机转子系统的固有频率偏低，在变频高速工况下会引起较大振动。通过对转子系统增加轴承支撑长度或增加轴承支撑数量，提升其固有频率，降低摆动转子压缩机高速运转时的振幅，并分析了两种方法的减振效果及优缺点，为摆动转子压缩机的设计与优化提供了理论依据。

摆动转子压缩机；转子系统；有限元；模态分析

0 引言

摆动转子压缩机70年代曾一度被使用，但由于其尺寸较大、加工较为复杂，80年代以后就很少使用。进入90年代，随着制冷剂的进一步研究与发展，其对压缩机的要求也不断提高，研究人员发现摆动转子压缩机比滚动活塞压缩机在某些方面具有明显的优势，因此又被个别制造厂大量生产[1]。随着摆动转子压缩机应用的增多，摆动转子压缩机的研究也越来越受到重视[2]。目前，因变频空调器具有快速制冷/制热、节能高效等优点[3,4]，变频技术被广泛应用于当前房间空调器中，从原来的30～120 Hz发展到十几年前的15～180 Hz，再到今天重点研究的10～250 Hz变频范围[1]，但随之而来的就是变频所引起的压缩机振动等问题，尤其是在高转速下，即高频工况下的振动问题。

在摆动转子压缩机中，偏心轮轴作为摆动转子压缩机的关键运动零件之一，为摆动转子提供动力，其运转速度高，承受载荷复杂，因此成为变频压缩机振动的来源之一。偏心轮轴作为压缩机动力输入，对其运动及振动情况的研究对摆动转子压缩机的发展具有重要意义。压缩机在工作过程中，由于偏心轮轴与电机转子、平衡重等是过盈配合，因此分析振动等问题时需将其视为压缩机的转子系统一起进行分析。本文通过SolidWorks软件建立三维实体模型，并利用有限元软件ANSYS Workbench对转子系统进行模态分析，确定其各阶固有频率和振型等振动特性，为摆动转子压缩机的设计制造提供了一定的技术参考。

1 模态分析理论

模态分析是用来确定结构的振动特性的一种技术，通过模态分析可以确定结构的自然频率、振型和振型参数。模态分析是利用有限元分析结构自然频率和模态振型的方法，其有如下假设：

（1）结构刚度矩阵和质量矩阵不发生改变；

（2）除非指定使用阻尼特征求解方法，否则不考虑阻尼效应；

（3）结构中没有随时间变化的载荷。

多自由度系统的一般微分方程为：

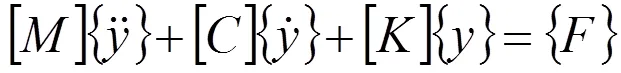
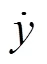
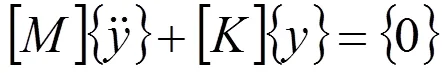
这是一个二阶齐次线性微分方程，其解的形式为：

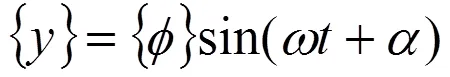
将式（3）代入式（2）可得：

上式方程组有非零解的充要条件为：

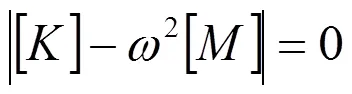
将上式展开可得到一个关于2的次代数方程，它的个根ω2（=1,2,3,...）即为系统的特征值，ω为结构的第阶固有频率。

将每个特征值ω2代入上式，得：

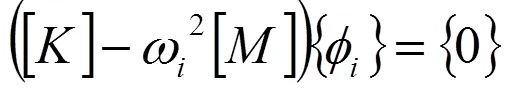
其中，{}为与特征值ω2对应的特征向量，{}即为结构的第阶主振型，将个特征矢量排列成一个×阶矩阵=[12…]，此为系统的特征矢量矩阵也称为模态矩阵[6]。

2 模态分析过程

本文利用ANSYS Workbench软件中的模态模块对转子系统进行有限元求解。ANSYS Workbench是ANSYS公司开发的协同仿真环境，其与经典ANSYS共用求解器，在保证精度的同时其操作更加人性化，目前被广泛应用于商业分析中。本文所涉及的模态分析主要步骤为：建立模型、前处理、施加边界条件、模态求解及查看结果。

SolidWorks软件是一种基于Windows开发的三维CAD系统，用其建立三维实体模型方便、快捷[7]。本文运用SolidWorks软件建立的转子系统模型，如图1所示。电机转子装配在偏心轮轴主轴尾段，并在转子两端设置平衡重，以平衡旋转时会产生较大的不平衡惯性力，减少振动等。上述零部件与主、副轴承一起构成用于分析的转子系统。

图1 摆动转子压缩机转子系统立体模型

2.1 前处理

对转子系统有限元模型进行模型简化，忽略一些不影响求解精度的、难以划分网格的倒角圆角、油路细节及电机转子中心的动态振幅[8]，在进行有限元分析前，需根据分析问题的几何结构、分析类型和所分析的问题精度要求等，选取合适的单元类型，本文选用三维八节点实体单元，这种单元类型每个节点有六个自由度[9]。把模型导入到有限元软件ANSYS Workbench中，并在材料属性选项中设置材料参数，偏心轮轴采用的材料是QT450-10，其弹性模量为1.69×105MPa，泊松比为0.257，密度大小为7060 kg·m-3，电机转子的材料采用铷磁铁，其弹性模量为1.6×105MPa，泊松比为0.3，密度大小为7500 kg·m-3。之后进入模态设置，设定相应的分析选项，并进行网格划分，由于六面体网格比四面体网格计算更精确且收敛性更好[10]，因此采用六面体网格进行划分，网格划分结果如图2所示，得到节点个数为114897，单元个数为31140。

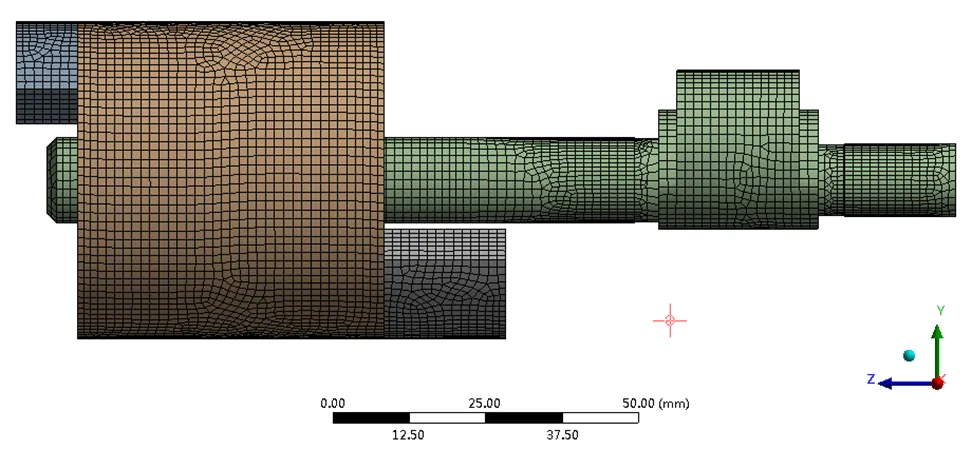
图2 转子系统网格划分模型

2.2 加载与求解

转子系统的固有频率与模态振型主要受到其结构及系统约束条件的影响，如图3所示，偏心轮轴主要受到主轴承和副轴承的约束，在主、副轴承（止推轴承）的支撑下，转子系统的轴向位移为零，其径向主要是轴承间隙的油膜力的支撑。因此在施加边界条件时，为了更好地模拟转子系统的实际情况，对其靠近副轴的止推面施加轴向零位移约 束[9]，轴承间隙的油膜可以简化为线性弹簧支 撑[11]，ANSYS Workbench提供了弹性约束方式来模拟弹簧的支撑作用，其刚度系数可由雷诺方程根据轴承的实际结构计算得到[12]，本文参考文献[8,12,13]并结合实际轴承的尺寸在轴承处施加弹性约束约束后即可进行模态求解。

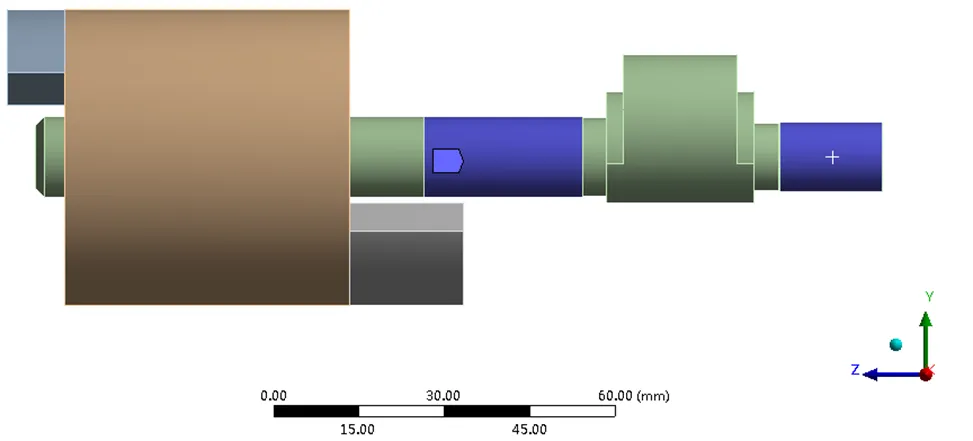
图3 转子系统施加约束模型

2.3 结果与分析

在进行模态求解前一般需要设置模态提取阶数，一般而言，频率最低的振型贡献最大，高阶振型的贡献较小[6]，因此本文提取了前6阶频率和振型进行分析。求解完成后，利用ANSYS Workbench软件生成的结果文件进行后处理。查看结果显示偏心轮轴的前6阶振型图如图4所示。

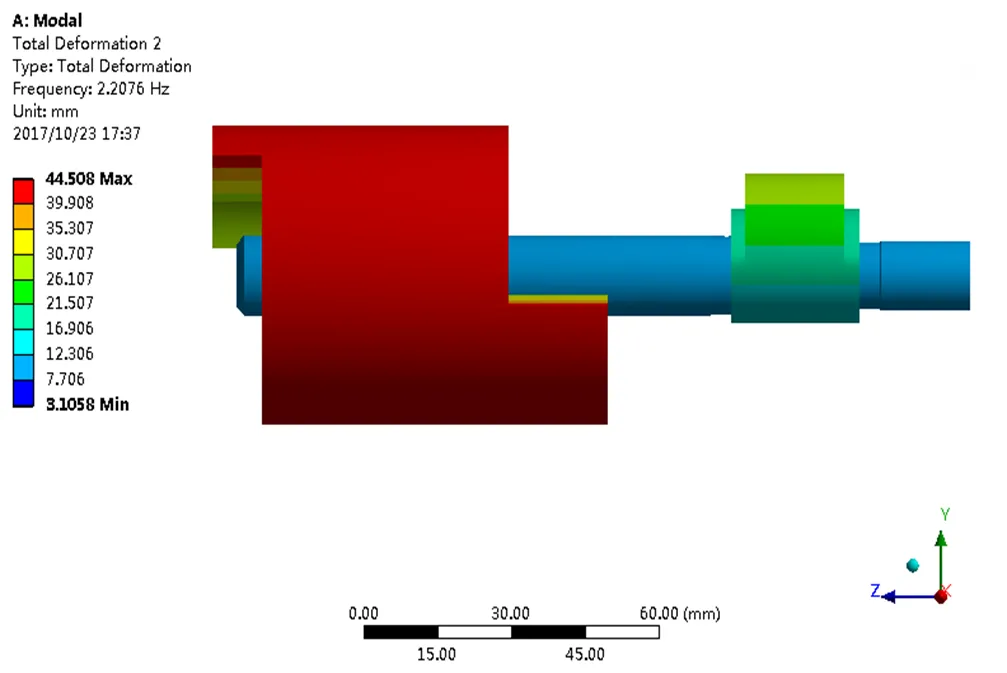
（a）第一阶模态

（b）第二阶模态

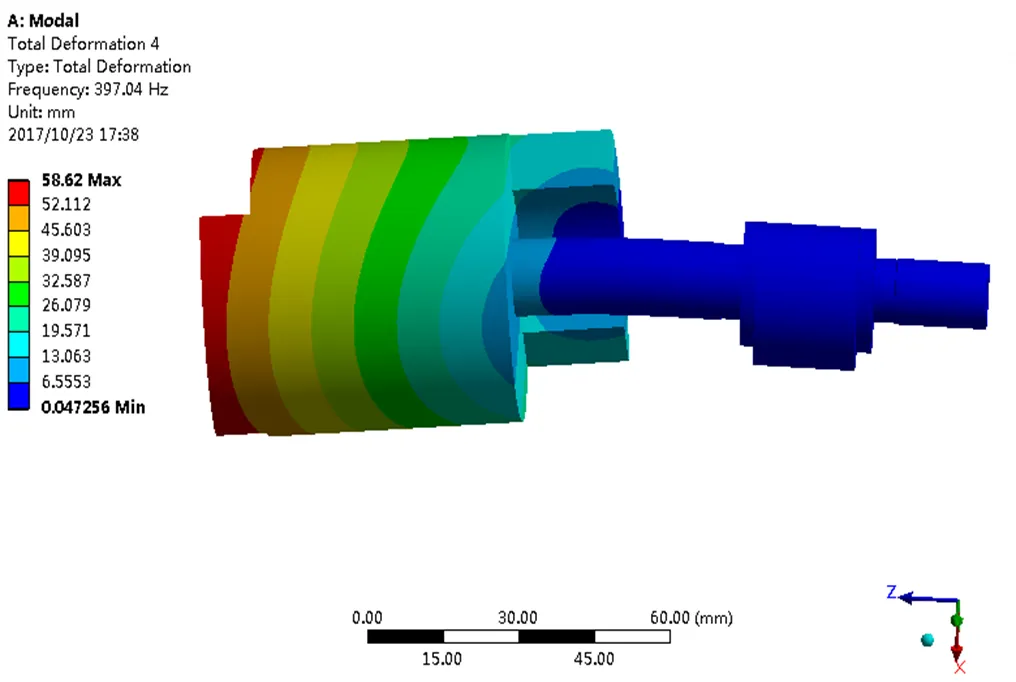
（c）第三阶模态

（d）第四阶模态

（e）第五阶模态

（f）第六阶模态

图4 转子系统前6阶模态

Fig.4 The modal shape of the first 6 orders of the rotor system

在压缩机的实际工作过程中，共振并不是当外界激励达到某阶固有频率时才发生的，而是当激励落在某一个共振区域内时即发生共振现象，振幅突然变大出现剧烈的振动。一般而言，这个共振区域是在固有频率的15%左右范围内[14]。从图4可以看出，转子系统的前6阶频率其共振区域主要发生在主轴段上，因此主轴是在外力激励下最可能发生共振的区域，也是偏心轮轴的设计者应该注意的部位。

当偏心轮轴旋转的角速度与其弯曲振动的固有频率相等时，偏心轮轴发生强烈的共振导致偏心轮轴寿命下降从而降低压缩机的可靠性，偏心轮轴此时的转速称为临界转速。当转速远离临界转速时，偏心轮轴运行平稳、不发生振动[15]。因此，对于设计者和操作者来说，使压缩机的工作转速远离临界转速，对确保压缩机工作的安全可靠性具有重要意义。临界转速与固有频率之间具有一定的关系，其关系式为：

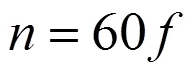
式中，为转子转速，r·min-1；为频率，Hz。

将模态分析得到的固有频率代入上式可得偏心轮轴固有频率和临界转速，如表1所示。

表1 转子系统各阶固有频率、临界转速及振型描述

从表1可以看出偏心轮轴的临界转速随着阶数的增加越来越大，而实际工作中的转速不会太大，因此只需关注转子的第1、2阶临界转速。其中，一阶固有频率为刚体模态，这是因为转子系统在旋转方向上的约束处于自由状态，因此其一阶频率理论上为零，但由于ANSYS Workbench中默认设置有微弱的阻力以及弹性约束的影响[5]，所以其一阶频率近似为零，一阶固有频率太低可以忽 略[16]。因此，为了使机器能够安全运行，要求工作转速远离第2、3阶临界转速，要求转子的工作转速应满足以下条件[15]：

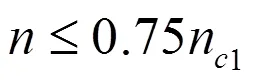
式中，表示转子的工作转速，r·min-1；n1表示转子基本阶临界转速，r·min-1。

从表1可以看出，偏心轮轴第2阶临界转速为23613 r·min-1，代入上式得≤17709.75 r·min-1，对于较低转速的压缩机而言，转子系统的工作转速已远离临界转速，运行平稳，不发生振动[15]，机器运行安全可靠。但对于现阶段所研究的高速机而言，转速可达到15000 r·min-1，该转子系统的工作转速虽然在理论安全范围之内，但已经很接近危险区，且压缩机振动与转子的转速有关，其次在实际工作中由于摆动转子所带来的不平衡力或随机振动及油膜震荡等因素会导致压缩机发生振动[17]，因此需要对转子系统进行改进，使其临界转速远离工作转速。本文根据隔振原理[6]提供了两种改进方案，一种是通过加长主轴承的方式以增加偏心轮轴刚度，另一种是通过在偏心轮轴主轴末端增加支撑的方式以增加偏心轮轴刚度[18,19]，以下分别对改进后的转子系统进行了模态分析并加以对比。

3 改进后的模态分析

3.1 方案一

改进后的转子系统模态分析方法与上述一致，方案一的转子系统模型与改进前的模型相差不大，只是在ANSYS Workbench中将主轴承约束相应的加长，约束如图5所示，然后进行模态分析。同样地提取前6阶频率和振型进行分析，查看结果显示转子系统的前6阶振型图如图6所示，频率与临界转速如表2所示。

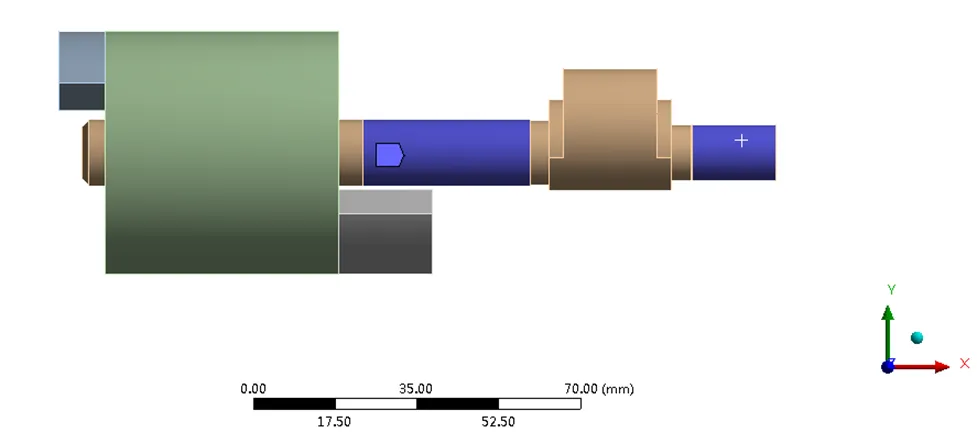
图5 转子系统施加约束模型

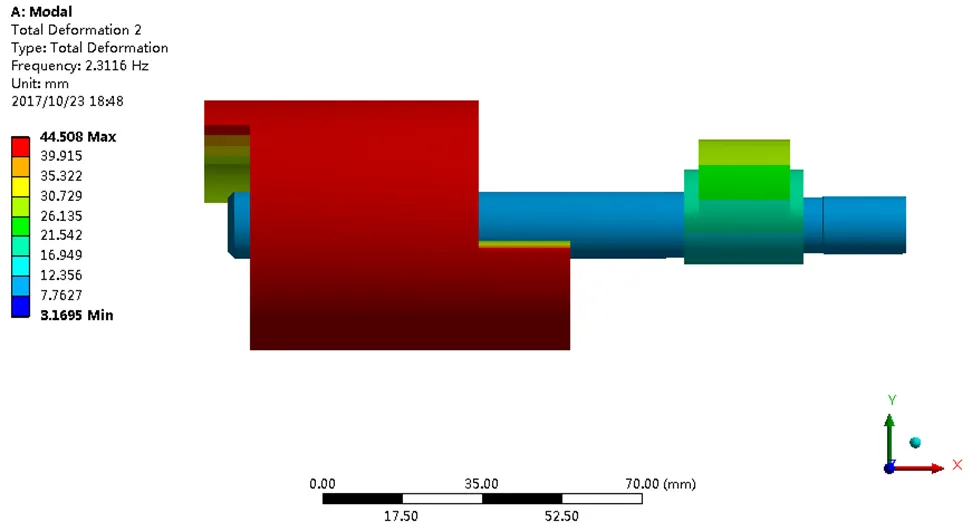
（a）第一阶模态

（b）第二阶模态

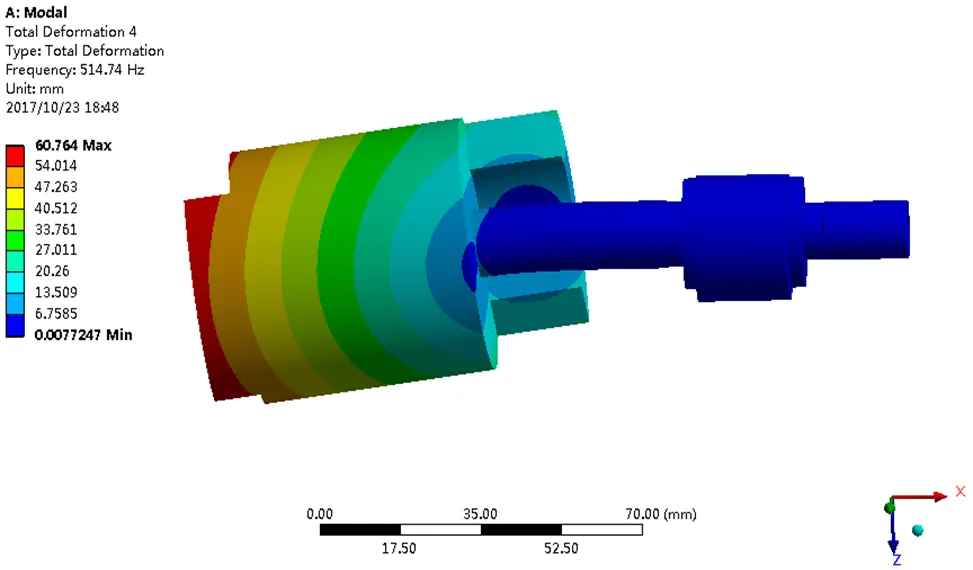
（c）第三阶模态

（d）第四阶模态

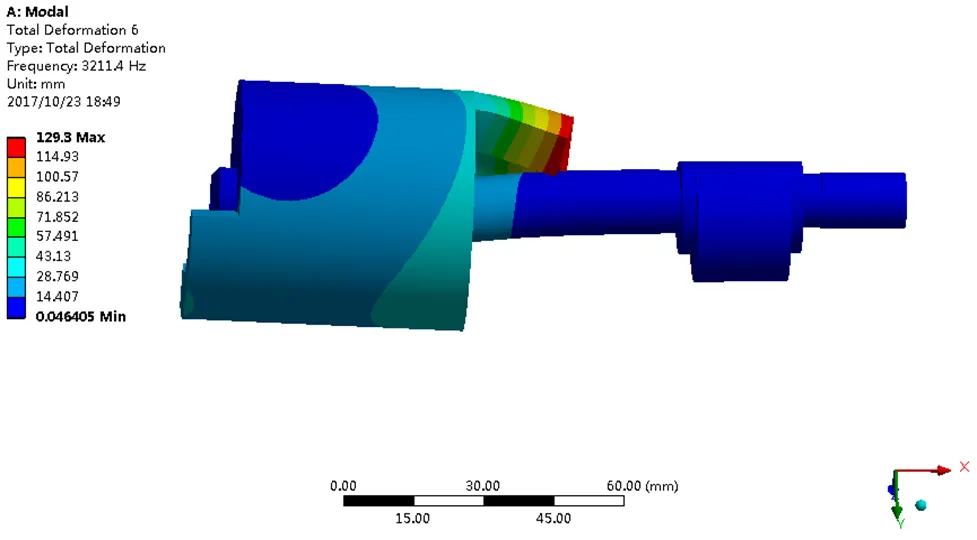
（e）第五阶模态

（f）第六阶模态

图6 转子系统前6阶模态

Fig.6 The modal shape of the first 6 orders of the rotor system

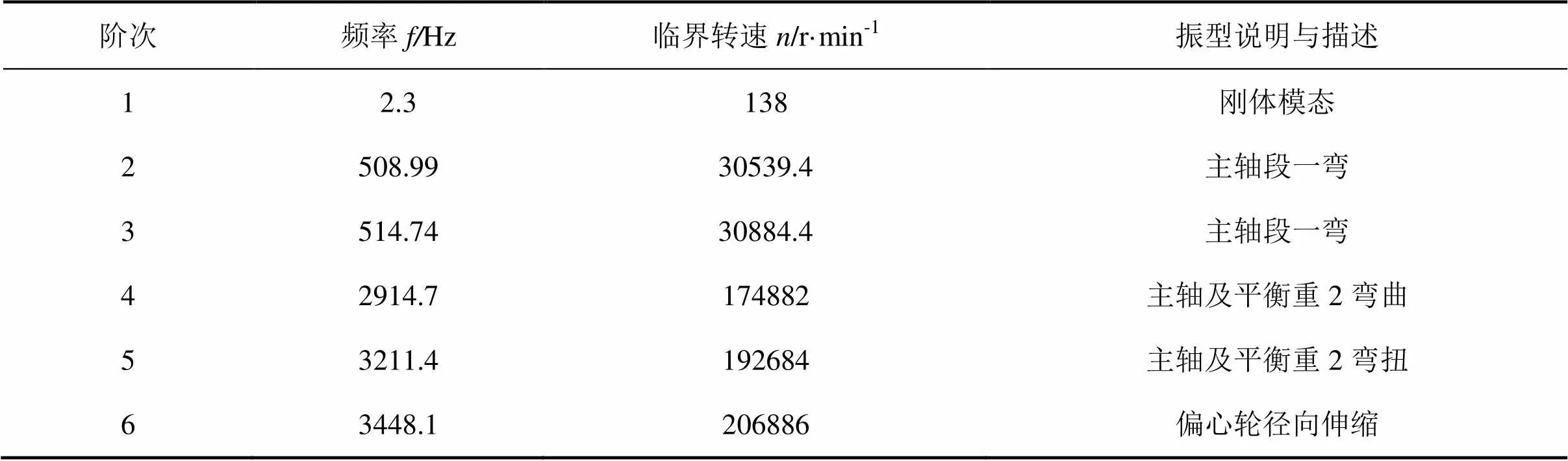
表2 转子系统各阶固有频率、临界转速及振型描述

从图6可以看出，方案一的转子系统各阶模态振型与改进前大体一致，对比表1和表2可以看出，加长主轴承的方式使得此系统的第2阶固有频率较改进前有一定的提高，相对于改进前其刚度增加，可靠性提高，但固有频率增幅较小，改善效果不明显。

3.2 方案二

方案二的模态分析过程与前述一致，运用SolidWorks建立的转子系统模型添加约束后如图7所示，其主轴末端的约束方式与主、副轴承的约束方式一致，在ANSYS Workbench中进行模态分析后得到的前6阶模态振型如图8所示，固有频率及临界转速如表3所示。

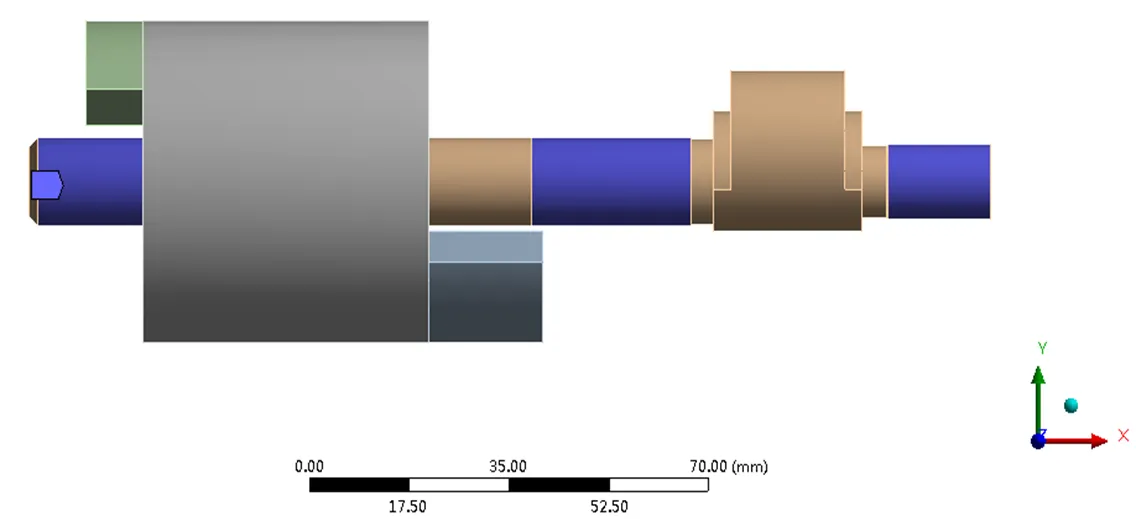
图7 转子系统立体模型

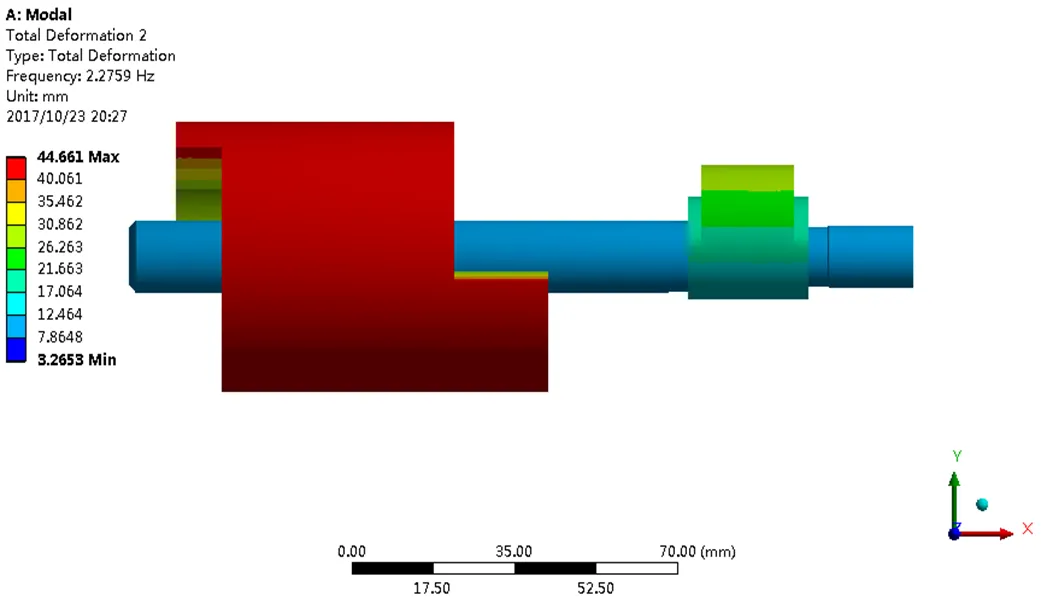
（a）第一阶模态

（b）第二阶模态

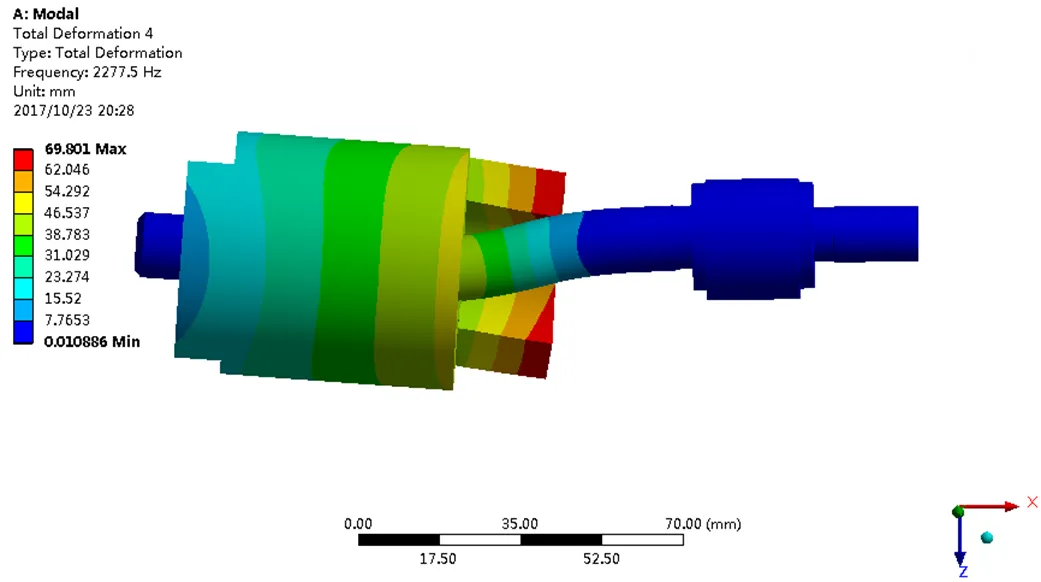
（c）第三阶模态

（d）第四阶模态

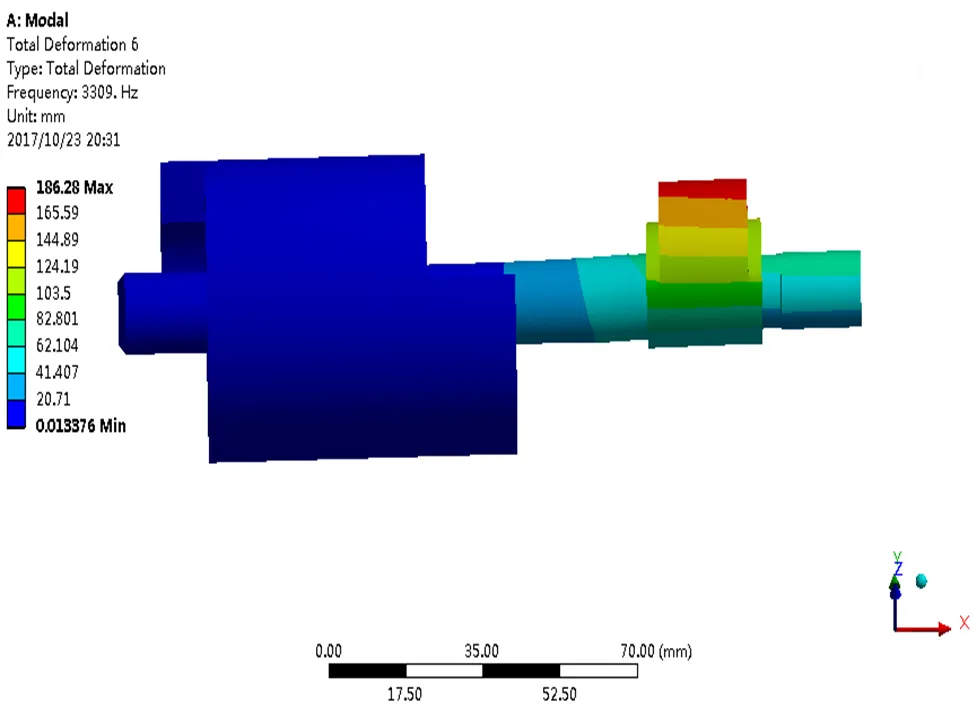
（e）第五阶模态

（f）第六阶模态

图8 转子系统前6阶模态

Fig.8 The modal shape of the first 6 orders of the assembly model of the rotor system

从图8和表3中可以看出，方案二的各阶模态振型与改进前有较大差异，其临界转速也得到了显著增加，这是由于在主轴末端增加约束后转子系统的刚度大幅上升，使其临界转速远远超过压缩机的工作转速，远离危险区域，从而使压缩机运行平稳，不发生振动。

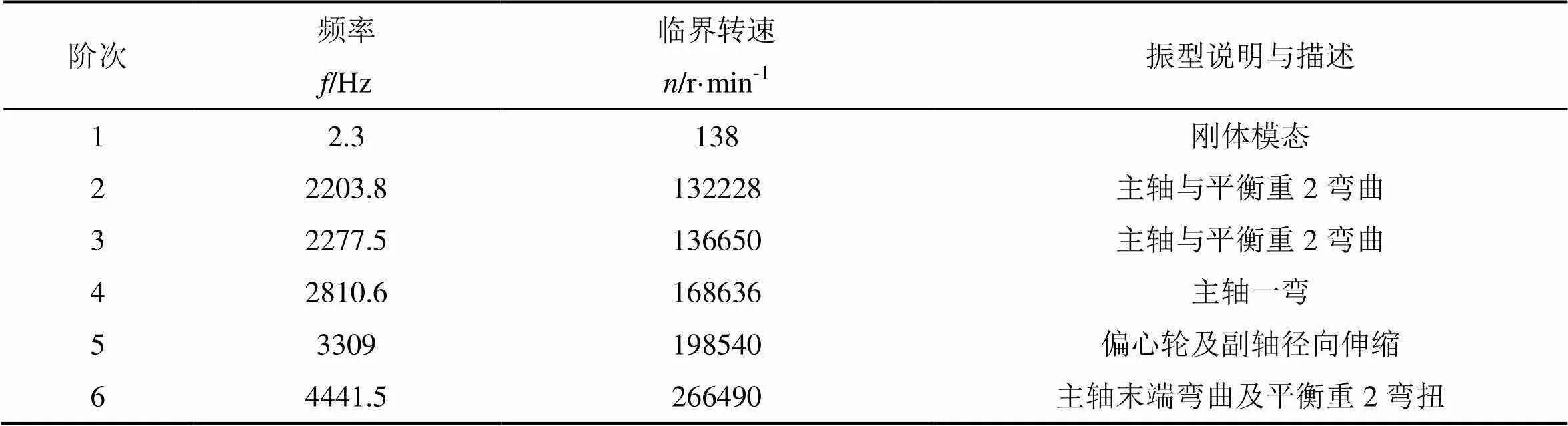
表3 转子系统各阶固有频率、临界转速及振型描述

4 结论

本文通过有限元软件ANSYS Workbench对摆动转子压缩机的转子系统进行模态分析，得到其前6阶固有频率和模态振型。通过对比变频压缩机工作转速与临界转速，发现该转子系统的临界转速偏低，在高速工况下会出现振动较大的情况。由此提出两种约束改进方案，并分别对转子系统进行模态分析得出以下结论：

（1）采用加长主轴承长度的方式，可以有效提升转子系统固有频率且加工简单，制造成本低，但临界转速增幅不大。

（2）采用在偏心轮轴末端增加轴承约束的方式，转子系统固有频率大幅上升，压缩机工作转速远离振动危险区，可靠性得到显著提高，但加工复杂，设计制造相对困难，成本相对较高。因此在实际设计生产中应综合选择合适的方法来减少压缩机高速运转时的振动问题。

[1] 马国远,李红旗.旋转压缩机[M].北京:机械工业出版社,2003.

[2] 王满,潘树林,周盛杰.摆动转子压缩机导轨处优化设计与泄漏分析[J].制冷与空调,2017,31(3):230-234.

[3] 丁强,王小华.变频空调压缩机频率控制算法的设计与研究[J].制冷与空调,2006,(3):49-52.

[4] 周智华,姚晓东.多温区汽车变频空调控制系统的仿真研究[J].制冷与空调,2008,22(3):53-56.

[5] 张东生,张建军.少齿数齿轮轴的模态分析与研究[J].机械设计与制造,2013,(8):210-212.

[6] 谢官模.振动力学[M].北京:国防工业出版社,2011.

[7] DS SolidWorks公司.SolidWorks高级教程:高级装配[M].北京:机械工业出版,2014.

[8] Hattori H. Dynamics analysis of a rotor-journal bearing system with large dynamic loads*(Stiffness and damping coefficient variations in bearing oil films)[J]. Jpn.Soc.Mech.Eng, 1993,36(2):251-257.

[9] Wang ZL, Yu XL, Liu FL, et al. Dynamic analyses for the rotor-journal bearing system of a variable speed rotary compressor[J]. International Journal Refrigeration, 2013,(36):1938-1950.

[10] 章兰珠,李仕云,郭军,等.直流变频空调室外机管路系统的模态分析[J].制冷与空调,2009,23(5):8-10.

[11] 张锁怀,李磊,张江峰.基于ANSYS的曲轴—滑动轴承系统动力学模型的研究[J].机械设计与研究,2007: 277-281.

[12] Mu HG, Zhang JQ, Xu XG, et al.Modal and harmonic response analysis of spindle system on CNC worm wheel gear grinding machine[J]. Hydromechatronics Engineering, 2014,42(12):29-33.

[13] Oscar DS, Edward A. Rotor dynamic analysis of a power turbine including support flexibility effects[C]. ASME Turbo Expo 2008: Power for Land, Sea, and Air. Berlin,Germany:International Gas Turbine Institute, 2008:1-9.

[14] 纵文斌,秦瑶,毛旭敏,等.平动回转压缩机滑片受力分析与临界转速的研究[J].压缩机技术,2015(4):11-16.

[15] 李云,姜培正.过程流体机械[M].北京:化学工业出版社,2008.

[16] 李春银,王树林.汽车空调旋叶式压缩机主轴转子的振动模型[J].制冷学报,2013,34(1):40-44.

[17] 杨峰,陈敬佑,方志民.回转式压缩机振动故障的时间序列分析[J].浙江工学院学报,1994,65(4):81-84.

[18] 李根周,徐弘锡,安宰赞,等.封闭式压缩机及其制造方法[P].中国:CN102235359A,2011.11.09.

[19] 张海峰,黄之敏,周忆.一种应用于压缩机的上支撑结构以及采用该结构的压缩机[P].中国:CN205101233U, 2016.03.23.

Model Analysis of Rotor System of Swing Compressor

Zhou Shengjie Pan Shulin Li Wei Rao Jinqiang

( Guangxi Key Lab. of Petrochemical Resource Processing and Process Intensification Technology, Guangxi University, Nanning, 530004 )

The dynamic model of rotor system which is consisted of the eccentric shaft and the motor rotor in swing compressor is established by using SolidWorks, and model analysis of rotor system is carried out by using ANSYS Workbench, then the natural frequencies and model shapes can be obtained. The results show that the natural frequency of the current rotor system is to so low that it can cause large shaking under the high speed working conditions. It found that the natural frequency is rose by increasing bearings' support length or its number of bearing, and the amplitude of the swing compressor is reduced when it operates at high speed. Moreover, the damping effect and advantages and disadvantages of this two methods are analyzed, and the research provides theoretical basis and references for the optimization design of the swing compressor.

swing compressors; rotor system; finite element; model analysis

1671-6612（2018）04-351-08

TB652

A

周盛杰（1991-），男，在读硕士研究生，研究方向为压缩机工作过程，E-mail：zhoushengjielun@163.com

潘树林（1970-），男，教授，博士，研究方向为压缩机工作过程，E-mail：panshulin@163.com

2017-10-25