翅片结构参数显著性影响分析及最优化

杨 勇 李夔宁 刘 彬 葛 玮 卞 煜



翅片结构参数显著性影响分析及最优化

杨 勇1,2李夔宁1,2刘 彬1,2葛 玮1,2卞 煜1,2

（1.重庆大学动力工程学院 重庆 400444； 2.低品位能源利用技术及系统教育部重点实验室 重庆 400444）

建立百叶窗式热交换器空气侧三维稳态对流换热数学模型，对不同几何特征参数的百叶窗式翅片进行了流动和换热数值模拟，采用因子、因子和因子分别对传热效率、流动性能以及综合性能进行评价。研究发现，百叶窗翅片的几何特征参数中百叶窗角度、百叶窗间距L、翅片间距F、翅片厚度对流动换热性能影响程度较大，选取这四个因素进行正交试验，得出翅片的最优结构参数。最优模型与基础模型相比，因子降低了7.7%，因子的值增幅为11.3%，综合评价因子的值增幅达到14.1%，表明优化后的翅片结构可以在压损增加较小的前提下有效的提升换热性能。

百叶窗翅片；传热流动；结构参数；最优化

0 引言

改善换热器的性能对空调功耗的降低有十分重要的现实意义。当采用铝制的百叶窗翅片换热器时，因其特殊的几何特征，不断地对边界层的破坏以及来流的扰动，来增强换热效率，从而使其具有紧凑高效的优良特性。所以，分析百叶窗翅片换热器的结构参数性能是十分必要的。然而，其在增加百叶窗翅片换热器的性能时，也会带来一定的不利作用，也就是让压降增加，从而增大风机的能耗。所以，在进行百叶窗翅片的设计时，一定要保证流动和换热处于均衡的状态。由于扁管内部冷凝相变换热的热阻较小，所以在换热器的整个热阻中，百叶窗翅片换热器的空气侧热阻不低于75%[2]，因此，减少空气侧热阻对于提升换热器的整体性能更加直接高效。

现有文献主要从百叶窗间距、角度及翅片间距三个方面分别研究其在百叶窗翅片换热性能达到最佳时的结构参数。在本文中，主要研究入口速度不变情况下，百叶窗式翅片的开窗角度、百叶窗间距L、翅片间距F、翅片厚度百叶窗转向区长度2等结构尺寸参数的改变对百叶窗翅片的传热效率和流动效率的影响，研究得出每个因素对流动换热性能的显著性等。选择对流动换热影响程度较大的四个因素进行正交实验，以此得出百叶窗翅片的最佳结构参数，且对最优结果仿真分析验证。

1 数值模拟

1.1 物理模型的建立

表1为百叶窗翅片基础模型的主要结构参数，其中的几何尺寸为当前主流技术使用的尺寸。

表1 百叶窗翅片主要结构参数

外部气体从百叶窗的前端流入，受到百叶窗的扰流，加强了气体与翅片间的换热。换热器芯体由多排等距（翅片间距F，如图1（b））的百叶窗翅片与扁管交叉排列而成。图1（c）为百叶窗式翅片的几何设计参数标示图。

为了准确的分析气体流经不同百叶窗翅片时的压损和换热变化，所有计算模型中，扁管几何尺寸为定值，不考虑其对流动换热产生的影响。在仿真的进程中，为了加快计算速度，仅选择百叶窗翅片的二分之一来进行计算，然后将其设置为对称性边界条件，从而完成翅片整场的数值分析。本文对CFD模型进行了如下的简化处理[6]：

介质为空气，其各物性参数不会随仿真过程中温度、压力等参数的改变发生变动，即各参数为恒定不变的；不考虑加工产生的形变和毛刺等现象，把各个翅片间的流道看作是一致的，而且扁管间距也保持一样；不考虑扁管内部含有内翅的情况；本文中，假设1=1，即仅研究百叶窗翅片侧截面上各结构参数，忽略翅片侧方向两端的结构。忽略辐射对温度场的影响。

1.2 数学模型及边界条件

对于有限体积法，恒定密度场，其直角坐标系下的连续微分方程为[5]：

对于不可压缩流体，粘性系数为恒定数值时，动量方程：

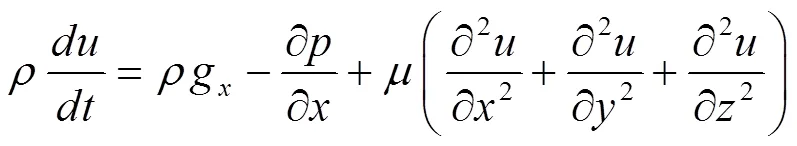
能量方程为：

图2为数学模型的边界条件，取7列翅片用作模拟计算，其中计算域入口和出口各延长30L，边界条件进行如下设置：入口设置成速度入口，T=294.15 K，出口设置成压力出口，压力为0 Pa，高度方向两侧壁面设为周期性边界条件，两扁管之间的中间面采用SYMMETRY边界条件，且设置扁管内壁恒定温度T=318.15 K，翅片与空气接触面设为耦合传热壁面。

本文选用三维稳态、基于压力、隐式求解器，SIMPLE算法，-模型和能量方程进行求解。

1.3 数据处理

本文选用因子和因子来评价百叶窗翅片的换热性能和流动性能[8]，综合性能因子评价百叶窗翅片的总体性能，其计算式如下：

式中，A为最小流通面积，m2；A为总换热面积，m2；ρ为空气的平均密度，kg/m3；1为入口处空气的密度，kg/m3；2为出口处空气的密度，kg/m3；K为突然收缩压力损失系数；K为突然扩张压力损失系数；为收缩比。

对数平均温差[7]表示如下：

综合性能因子[9]定义如下：

定义影响程度P[10]为：

式（12）中，为几何参数，X和JF分别为基础模型的几何参数和因子。表示方差，可表示为：

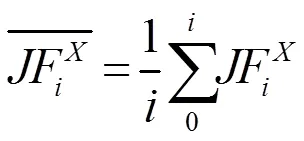
1.4 数学仿真模型有效性验证

本文选择了当流体域进口温度T=294.15 K，扁管内壁温度T=318.15 K，选取雷诺数Re=700～3000范围内空气穿过翅片的流动换热情况和实验进行对比验证。

图3 数学仿真模型和实验对比验证

图3为仿真模型和实验的对比验证，把摩擦因子和实验进行对比，可得出不同雷诺数下误差均小于10%。CFD仿真模型无法考虑试验样件因加工粗糙带来的一定程度的尺寸误差以及表面粗糙度等因素对流动换热的影响。所以本文所建立的CFD模型是合理有效的。

2 结果与分析

2.1 开窗角度θ对流动换热性能的影响分析

选取五个水平下的百叶窗翅片开窗角度：24°，27°，30°（基础模型），33°，36°，研究百叶窗翅片的传热和流动性能在不同开窗角度下的变化规律。

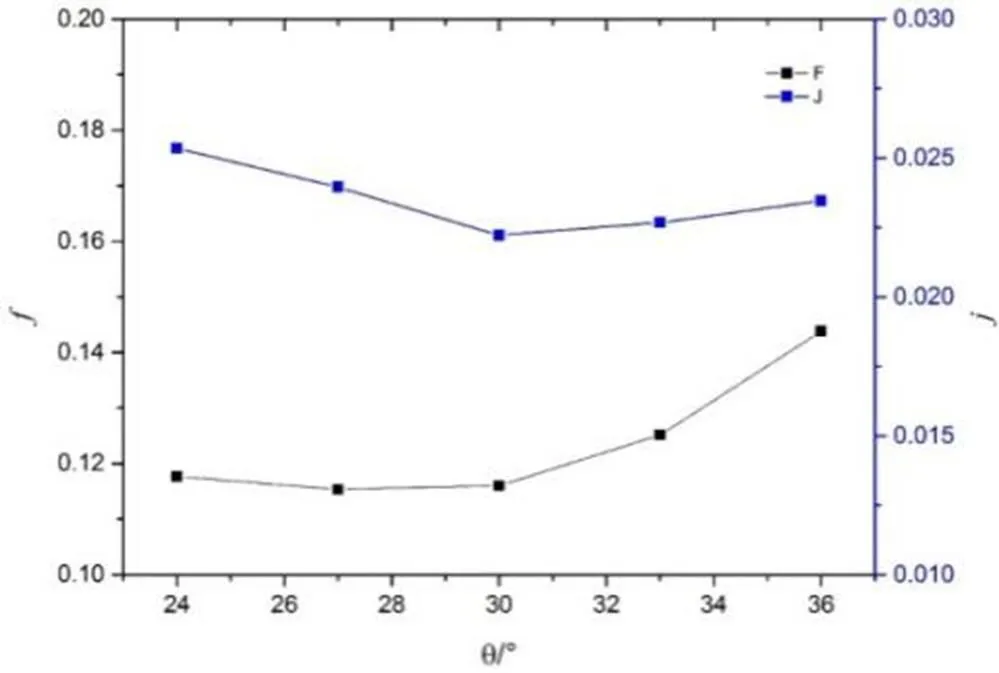
图4 不同百叶窗翅片角度θ时j因子与f因子

从图4分析可得，因子与因子的变化趋势相同，呈现先抑后仰的趋势。表明若换热性能提高了，则流动阻力必然增加。其中翅片开窗角度的改变对流动的影响更甚，主要原因对来流空气的强制扰动随着翅片角度的逐步增加而增加，流入翅片开窗角的空气量增多，流动阻力变大。同时穿过芯体的空气与翅片表面的碰撞会带来局部损失，若开窗角度加大，局部损失也会进一步变大，以致流动性能变差。

2.2 百叶窗间距Lp对流动换热性能影响分析

选取五个水平下的百叶窗间距L：0.98 mm、1.08 mm、1.2 mm（基础模型）、1.35 mm、1.54 mm，研究翅片的传热和流动性能在不同百叶窗间距L下的变化规律。

图5 不同百叶窗间距Lp时的j因子和f因子

从图5分析可得，因子随着百叶窗间距的增大先降低后缓慢增加，而因子随之缓缓减小。流动性能最好的百叶窗间距为1.2 mm，该点因子值最小。百叶窗间距为0.98 mm和1.08 mm下的因子相差较小，即换热效率变化幅度不大。若芯体厚度不变，L增加，百叶窗数量变少，对来流空气扰动变弱，会造成传热效率的降低和流动效率的提高。其间距减小到一定时，传热因子相对于基础模型增幅变化不大。

2.3 翅片间距Fp对流动换热性能影响分析

选取五个水平下的翅片间距F：1.13 mm、1.23 mm、1.33 mm（基础模型）、1.43 mm、1.53 mm，研究翅片的流动传热性能在不同翅片间距F下的变化规律。

图6 3不同百叶窗翅片间距Fp时的j因子和f因子

由图6分析可得，当翅片间距F增加时，因子呈现先抑后仰趋势。当间距从1.33 mm降至1.23 mm时，因子相对于基础模型的增长比最大，达到8%。亦是因子幅值最高点，说明此时换热性能最优。因子值在间距为1.33 mm时最小，流动效率最高。增大翅片间距，在芯体尺寸不变时，芯体横向翅片的列数将减少，肋化系数明显降低，换热性能将下降。较小的翅片间距可以提升肋化系数，增强换热能力，但是会增加换热器通过阻力。因此，在实际工程应用中，可通过综合因子平衡换热和流动，使其达到最优。

2.4 翅片厚度δ对流动换热的影响分析

选取三个水平下翅片厚度：0.06 mm、0.08 mm、0.1 mm，研究翅片的传热和流动性能在不同百叶窗翅片厚度下的变化规律。

图7 不同翅片厚度δ时的j因子和f因子

从图7可知，当翅片厚度为0.1 mm时，传热因子的值位于最高点，传热效率最好。当翅片厚度的增加，因子增大，换热性能逐步提升，但是其增幅降低。然而当百叶窗翅片厚度增大时，较小的增幅伴随着更大的因子的增长。因此，不能为了获得更好的换热任意增加翅片厚度，需要将换热和流动结合考虑。

2.5 百叶窗转向区长度S2对流动换热性能影响分析

选取百叶窗四个水平下的转向区长度2：1 mm、1.2 mm、1.4 mm（基础模型）、1.6 mm，研究翅片的传热和流动性能在不同转向区长度2下的变化规律。

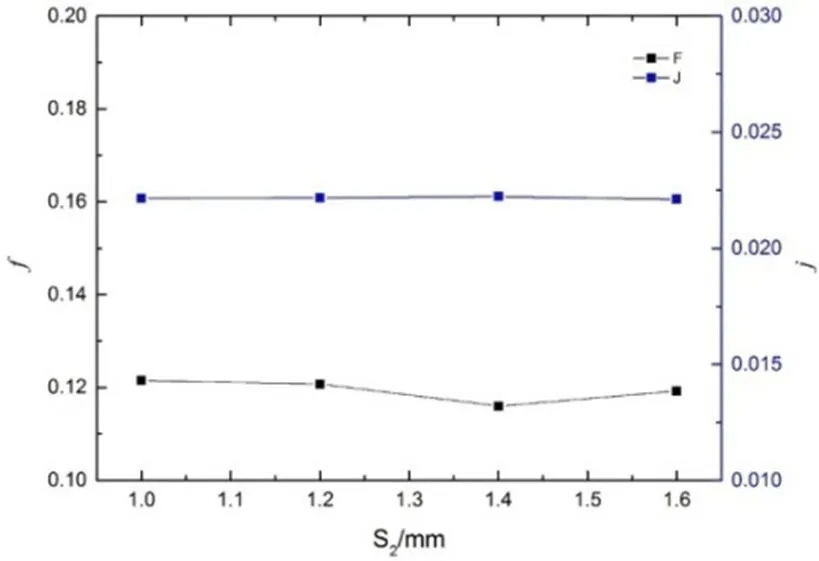
图8 不同百叶窗转向区长度S2时j因子和f因子

由图8分析可得，转向区长度2在1～1.6 mm范围内的变动对传热和流动性能的影响很小。基础模型转向区长度因子值最小，表明此时流动性能最好。

2.6 不同结构参数显著性分析

因子用以分析百叶窗翅片的总体性能，其同时考虑了传热和流动两个方面的因素。表2是不同结构参数时的因子，在这些因子的基础上，计算得到不同因子的影响程度P。

表2 结构参数显著性影响分析

本文在该部分计算过程中是以基础模型的翅片为基准的，其各项参数分别为：=30º，L=1.2 mm，F=1.33 mm，=0.08 mm，2=1.4 mm，评价结果如图9所示。

图9 结构参数对JF因子的显著性影响分析

从图9得出，开窗角度的值最大为0.42，说明它能最大程度影响翅片的流动换热性能。之后的是百叶窗间距L与翅片间距F，它们的值相近，对总体性能的影响程度基本相同。而其值变化对总体性能影响不大的是翅片厚度和百叶窗转向区长度2。

3 翅片结构参数的最优化

在正交实验中，选取对翅片流动传热性能影响最大的四个参数结构，同时选取每个参数结构较优的数据值。在本文研究中，选取翅片间距F（F=1.23 mm、1.33 mm、1.43 mm）、百叶窗角度（=24°、27°、30°）、百叶窗间距L（L=0.98 mm、1.08 mm、1.2 mm）、翅片厚度（=0.06 mm、0.08 mm、0.1 mm）4个结构参数、3个水平取值作为实验变量设计正交实验，为几何结构参数的最优化提供依据。在常规的实验中，由于含有4个结构参数，这4个参数又包括3组数据，共有43=64种组合方式，需进行大量的实验次数。本研究采用正交实验表L9（34），按照该表仅需进行9次试验，详见实验方案表4。表3为正交试验因素水平表。

表3 正交试验因素水平表

图10 Case1～9的综合性能JF因子对比

表4 实验方案表

图10是不同实验方案下的综合性能因子的计算值。可以得出，Case1（F=1.23 mm、=24°、L=0.98 mm、=0.06 mm）的因子的值最高，说明Case1所对应的实验方案综合性能最优。其中表5对比了最优模型Case1与基础模型的性能指标。

表5 优化模型与基础模型的各项性能参数

从表可以得出，与基础模型相比，Case1的因子值降低了7.7%，因子的值增加了11.3%。所以，最优模型Case1的因子总体提高了14.1%，在控制压降增大的基础上，实现了换热效率的提高。

4 结论

本文主要对翅片5个结构参数进行数值仿真分析，各自分析了5个结构参数对翅片换热和流动的影响规律，以及各参数对流动换热性能贡献程度的研究，结合正交实验对结构最优化设计进行指导，得出以下三点结论：

（1）当进口速度条件不变时，开窗角度的变大，因子会呈显出先减小后缓慢增加变化曲线，但是因子则是递增幅度逐步变大；当百叶窗间距L变大时，因子呈逐步降低趋势且递减幅度渐渐变小，因子变化趋势与因子大致相同，前期递减幅度更加明显；当翅片间距F变大时，因子和因子均呈现出先减小后缓慢增大趋势；当翅片壁厚递增时，因子增加不明显，因子增大趋势不断变大；而转向区长度2的增减引起的流动和换热性能变动很小。

（2）百叶窗翅片各个几何特征尺寸的变化对流动换热性能显著性的贡献度由高到低依次排序为：、L、F、、2。所以，在实际工程应用开发中，可以主要关注翅片结构的开窗角度、翅片间距（翅片波距）、百叶窗间距（开窗数）以及翅片的厚度。

（3）选取百叶窗翅片结构参数中对流动换热影响严重的四个因素（、L、F、）进行了三个水平取值L9（34）的正交实验。其中Case1模型（F=1.23 mm、=24°、L=0.98 mm、=0.06 mm）的因子的值最高，流动传热性能达到最优。最优的模型与基础模型相比较，优化模型因子值降低了7.7%，因子的值增加了11.3%，同时综合评价因子的值增幅为14.1%，达到换热效率明显改善且使得压降变化不大的理想效果。

[1] 王丹,董其伍,刘敏珊.车辆散热器祸合传热模拟研究[J].工程热物理学报,2011,32(10):1727-1730.

[2] I Taymaz, K Cakir, M Gur, et al. Experimental investigation of heat losses in a ceramic coated diesel engine[J]. Surface and coatings technology, 2003,169:168 -170.

[3] MH Kim, CW Bullard. Air-Side heat transfer and pressure drop characteristics of multilouvered fin and flat tube heat exchangers[C]. in: Proceedings of the ASME Advanced Energy Systems Division, AES, 2002,40:191- 198.

[4] 寇磊,廖胜明,刘玉涵.百叶窗翅片传热特性的数值模拟[J].建筑热能通风空调,2009,28(1):6-9.

[5] PJ Roache. Computational fluid dynamics[M]. Hermosa publishers, 1972.

[6] 韩占忠,王敬,兰小平.FLUENT-流体工程仿真计算实例与应用[M].北京:北京理工大学出版社,2008.

[7] 杨世铭,陶文铨.传热学[M].北京:高等教育出版社,2006: 212,307.

[8] CC Wang, KY Chi, YJ Chang, et al. An experimental study of heat transfer and friction characteristics of typical louver fin-and-tube heat exchangers[J]. International journal of heat and mass transfer, 1998,41: 817-822.

[9] K Ryu, KS Lee. Generalized heat-transfer and fluid-flow correlations for corrugated louvered fins[J]. International journal of heat and mass transfer, 2015,83:604-612.

[10] 盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2008.

[11] lyman A C. scaling of heat coefficients along louvered fins[J]. Experimental Thermal Fluid science,2002,(26): 547-563.

[12] Suga K, Shingawa T. Numerical analysis on two-dimensional flow and heat transfer of louvered fins using overlaid grids[J]. JSME Int J Ser, 1990,33:120-127.

[13] Aoki H, Shingawa T, Suga K. An experimental study of the local heat transfer characteristics in automotive louvered fins[J]. Experimental Thermal and Fluid Science,1989,(2):293-300.

Influence Analysis and Optimization of Fin Structure Parameters

Yang Yong1,2Li Kuining1,2Liu Bin1,2Ge Wei1,2Bian Yu1,2

( 1.College of power engineering, Chongqing University, Chongqing, 400044; 2.Low grade energy utilization technology and system State Key Laboratory of Ministry of Education, Chongqing, 400044 )

A mathematical model of three-dimensional steady convection heat transfer in the air side of louvered fin heat exchanger is established. Numerical analysis is performed separately on the louver fin with different structure parameters.factor,factor andfactor are used to evaluate heat transfer, flow performances and final performances. Numerical analysis shows that,L,Fandcan influence the final performance of the fin considerably. The orthogonal test is carried out onF,,Landfour factors and the optimal structure parameters of fin is obtained. Compared with the original model, thefactor of the optimal model is reduced by 7.7%, the value of thefactor is increased by about 11.3%, and thefactor of the optimized model is increased by about 14.1%. The result shows that the optimized louvered fin can effectively improve the heat transfer performance under the condition of less pressure loss.

louvered fin; heat transfer and flow performance; structure parameters; optimization

1671-6612（2018）04-343-08

TB657.5

A

中央高校基本科研业务费科研专项（编号：CDJZR14140002）

杨 勇（1992-），男，在读硕士研究生，从事汽车空调系统的研究，E-mail：417102552@qq.com

李夔宁（1970-），男，教授，博士生导师

2017-09-13