不确定环境下闭环供应链的回收—生产—分销协同计划

景 熠，李文川，周 旖

(1.重庆理工大学 管理学院，重庆 400054；2.南昌航空大学 经济管理学院，江西 南昌 330063；3.重庆理工大资产经营管理有限责任公司，重庆 400054)

0 引言

随着经济全球化趋势的不断加强，以及信息技术的蓬勃发展，单一企业之间的竞争已逐步转变为供应链之间的竞争。毫无疑问，供应链中任何一个成员企业的不合作、不协同，都将影响整个供应链网络的运作绩效。将供应商、制造商、分销商或者零售商分割开来，独立地制定相应的运作计划，在当前经济全球化背景下存在两方面问题：①单一成员企业收益的最大化，并不代表整个供应链体系收益的最大化，甚至会损害上下游其他企业的利益；②单一成员企业的计划制定得再完美，若供应链上下游的其他企业不配合，则计划无法充分实现，甚至会影响整个供应链体系的正常运转。

因此，一些学者将供应链运作中的生产和分销两个主要问题结合起来，进行了生产—分销协同计划的研究。Manzini等[1]首先针对由一个制造工厂、多个区域分销中心和多个客户需求点组成的三阶段供应链网络，建立了面向单产品生产和流通的协同计划模型，然后将该模型拓展到面向多产品族的情形;Gebennini等[2]在文献[1]模型的基础上，考虑各个区域分销中心的安全库存问题，探讨了安全库存对运作成本和产品交付率的影响;Amorim等[3]针对具有固定保质期和可变保质期的两种易逝产品分别建立了相应的协同计划模型，根据问题的特点，以最小化运作总成本和最大化平均剩余保质期作为运作优化目标;Liu等[4]以最小化总成本、最小化运输时间和最小化缺货数量作为供应链网络的运作目标，建立了相应的多目标协同计划模型，并利用ε约束方法和字典序极小极大化方法进行求解;李应等[5]针对由多个工厂、多个分销中心和多个零售商组成的供应链网络，利用多层规划的方法建立了分布式三层协同计划模型;蒋国瑞等[6]考虑了非对称信息条件下，多层分布式供应链网络的协同决策问题，利用多层规划的方法构建了相应的生产—分销协同计划模型;Husseini等[7]建立了面向多制造商、多分销商和多需求中心的协同计划模型，并以最小化生产—分销总成本和最大化产品供应质量为优化目标。在此基础上，一些学者进一步考虑原材料供应环节，进行了供应—生产—分销协同计划的研究。Gholamian等[8]针对由多个供应商、多个制造工厂和多个最终需求点组成的三阶段供应链系统，建立了协同计划模型，以最小化总成本和最小化缺货率作为运作目标;马慧民等[9]针对由多个供应商、多个制造工厂和多个最终需求点组成的三阶段供应链网络，以最小化总成本为运作目标，建立了考虑价格折扣的协同计划模型;Yllmaz等[10]针对由多个供应商、多个制造工厂和多个分销中心组成的三阶段供应链网络，建立了允许生产能力扩充的协同计划模型，根据模型特点，以最小化常规运作成本和能力扩充成本的总和作为优化目标。

另一方面，随着自然资源枯竭和环境问题的日益严重，废旧产品的回收再利用和资源化处理受到了社会的普遍关注，许多国家已经立法，责令企业要对产品的整个生命周期负责，以期节约资源和保护环境。越来越多的企业也更加主动地对处于生命周期末端的产品进行回收和再处理，进而实现价值增值。通过再制造等方式，“资源—生产—消费—废弃”的开环过程正在向“资源—生产—消费—再生资源”的闭环供应链运转方式转变。因此，闭环供应链管理的研究受到越来越多的重视，在设施网络规划[11-12]、牛鞭效应分析[13-14]、产品定价策略[15-16]和契约协调策略[16-18]等方面取得了较为丰富的研究成果。然而这些研究主要侧重战略与战术层面，有关运作层面(或执行层面)的研究则略显不足。晏妮娜等[19]针对由一个供应商和一个制造/再制造工厂组成的闭环供应链系统建立了运作计划模型，徐家旺等[20]在此基础上进一步考虑了顾客需求的不确定性;陈新林等[21]建立了一类基于单方决策的、具有供应商竞争和顾客需求不确定的闭环供应链生产计划优化模型。这些研究所考虑的研究对象都是以单节点生产工厂为中心的单链式闭环供应链，无法体现协同效应，所考虑的不确定因素也仅为市场需求的不确定性。

因此，本文借鉴正向供应链协同计划的研究思想，针对由一个进行拆卸、检验的联合回收中心，多个进行制造和再制造的生产工厂，以及多个进行销售和下游回收的分销中心组成的三阶段闭环供应链网络，充分考虑市场需求和废旧产品供应情况的不确定性，建立回收—生产—分销三层协同计划模型，并基于决策交互的特点，设计分层迭代整体求解策略，在单层求解过程中设计双倍体自适应遗传算法(Double Chromosomes Adaptive Genetic Algorithm, DCAGA)。本文在正向供应链协同计划研究的基础上，进一步考虑第三方回收渠道，以及拆卸、检验、再制造和再销售等逆向活动对成员企业协同运作的影响，构建面向闭环供应链协同网络的运作计划模型，该模型能够对各个成员企业的运作进行统一的计划和安排，实现正、逆向活动的协调，并综合考虑回收产品供应数量的不确定性和市场需求的不确定性。

1 问题描述

本文所考虑的三阶段闭环供应链网络，由一个进行拆卸、检验的联合回收中心，多个进行制造和再制造的生产工厂，以及多个进行销售和下游回收的分销中心组成，其基本的网络结构如图1所示。

联合回收中心负责将回收产品拆卸为各个核心组件，并进行检验。经检验合格的、可用于再制造的核心组件将被存放于库存中，而对损坏程度较大、难以通过再制造进行修复的核心组件将进行环保废弃处理。根据不同的生产需求，联合回收中心将可用于再制造的核心组件运往各个制造/再制造工厂。

各个制造/再制造工厂可以投入原材料进行新核心组件的生产，也可以通过再制造工艺技术对回收中心运送来的核心组件进行再生产，恢复其质量和性能；而新生产的核心组件用于装配新产品，再生产的核心组件用于装配再制造产品。根据不同的订单需求，各个制造/再制造工厂将新产品和再制造产品运往下游各个分销中心。

各个分销中心可以选择一个或多个制造/再制造工厂为其提供产品和服务，并向下游的零售商或客户销售新产品和再制造产品。同时，分销中心还负责从下游零售商和客户手中回收处于生命周期末端的产品运往联合回收中心。

根据模型建立的实际情况作如下说明：

(1)联合回收中心在考虑回收处理成本、预期销售情况和目标收益等因素的基础上，对可用于再制造的核心组件进行统一定价，但针对新建工厂或新生产线导入等情况，可能会在短期内给予一定的价格支持。

(2)由于各个制造/再制造工厂所在地域的劳动力市场以及自身生产力水平不同，即便生产相同类型的产品或核心组件，不同工厂之间的生产成本也可能不同。

(3)由于各个分销中心所在地域的消费情况和企业销售策略不同，即便向下游客户销售相同类型的产品，或从下游客户回收相同类型的产品，不同分销中心之间的销售价格或回收价格也可能不同。

(4)由于各个工厂和分销中心所在地域不同，不同节点企业之间的运输成本也存在一定差异。

(5)为聚焦研究重点，本文所考虑的不确定因素仅包括新产品和再制造产品市场需求的不确定性，以及废旧产品供应数量的不确定性。

2 模型基本变量和参数

2.1 下标

回收—生产—分销三层协同计划模型中涉及的下标符号及其含义如表1所示。

2.2 变量

按照在模型中的出现顺序，对三层协同计划模型的变量含义进行说明，如表2～表4所示。

2.3 参数

按照在模型中的出现顺序，对三层协同计划模型的参数含义进行说明，如表5～表7所示。

3 不确定环境下回收—生产—分销三层协同计划模型

闭环供应链网络的协同计划分为联合回收中心、制造/再制造工厂和分销中心3个阶层。在目标上，联合回收中心、制造/再制造工厂和分销中心都以追求自身利润最大化为目标。该问题属于一个多层递阶结构的分散决策问题，即在一个完整的运作系统中，存在多个利益集团和决策者，每一个利益集团的决策者拥有各自不同的目标，这些目标之间是相互关联的。多层规划是研究复杂分散决策问题的一种有效方法，通过多层规划方法建立的协同计划模型，其各个层次的决策者被赋予不同的决策权限，允许在权限范围内制定自己的计划。上层的决策会对下层的计划产生影响，进而影响下层目标的达成，但无法完全控制下层的决策和计划；当下层计划制定出来后，又会对上层目标的实现产生影响。

在实际商业运营过程中，大多数企业都会通过历史信息对未来的市场情况进行预测，并根据预测制定相应的计划。但基于对市场走向(如市场情况良好、一般和欠佳等)的不同判断，可能会产生多组不同的预测数据，而企业往往会从中选择可能性最大的一种作为计划的依据。然而这样制定出来的计划在市场走向发生偏离时将可能失效，无法应对市场的不确定性影响。因此，本文基于情景分析描述新产品、再制造产品市场需求和废旧产品供应数量的不确定性，在预测数据的基础上进一步考虑各种市场走向的概率并综合考虑所有可能的情况。

根据情景分析方法，新产品市场需求、再制造产品市场需求和回收产品供应数量可以分别用S1个新产品需求情景s1、S2个再制造产品需求情景s2和S3个回收情景s3描述。prs1是新产品需求情景s1(1,2,…,S1)的发生概率，prs2是再制造产品需求情景s2(1,2,…,S2)的发生概率，prs3是回收情景s3(1,2,…,S3)的发生概率。因此，市场需求和回收产品供应数量不确定的闭环供应链协同计划包含了S(S=S1·S2·S3)个预测情景s，每一个情景表示一组回收情况和需求情况的预测值。prs(prs=prs1·prs2·prs3)是预测情景s(1,2,…,S)的发生概率。

各层的数学模型分别表示如下：

(1)第一层：联合回收中心

联合回收中心以最大化自身收益为运作目标，其中收入部分为可用于再生产的核心组件的销售总额，成本部分为运输成本、环保废弃成本、库存成本、回收成本、拆卸检验成本的总和，表示为

SDTpt·σpt+UDTCpt·dtpt·dtbp+

(1)

同时，该层模型还应满足下列约束：

1)回收产品的库存平衡公式

dtbp,∀p,t,s。

(2)

2)经拆卸后得到的核心组件的库存平衡公式

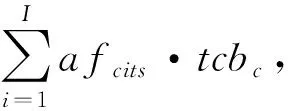
(3)

3)核心组件废弃处理数量约束

(4)

4)库存能力约束

∀t,s;

(5)

(6)

5)拆卸、检验能力约束

dtpt·dtbp≤MDTp·σpt,∀p,t。

(7)

6)运输能力约束

∀t,s。

(8)

7)非负整数约束

(9)

(2)第二层：制造/再制造工厂

制造/再制造工厂以最大化自身收益为运作目标，收入部分为新产品和再制造产品面向分销中心的销售总额，成本部分为运输成本、制造成本、再制造成本、库存成本、核心组件回购成本的总和，表示为

fdnpijts·tpbp+MPRpijt·fdrpijts·tpbp-

SApit·ηpit-UACpit·xpit·abp-SRApit·δpit-

afcits·tcbc]}。

(10)

同时，该层模型还应当满足下列约束：

1)经拆卸后得到的核心组件的库存平衡公式

zcit·rpbc,∀c,i,t,s。

(11)

2)新核心组件的库存平衡公式

(12)

3)恢复核心组件的库存平衡公式

(13)

4)新产品的库存平衡公式

(14)

5)再制造产品的库存平衡公式

(15)

6)库存能力约束

∀i,t,s;

(16)

(17)

(18)

(19)

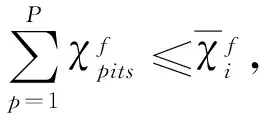
(20)

7)生产能力约束

vcit·pbc≤MPci·πcit,∀c,i,t;

(21)

zcit·rpbc≤MRPci·τcit,∀c,i,t;

(22)

xpit·abp≤MApi·ηpit,∀p,i,t;

(23)

ypit·rabp≤MRApi·δpit,∀p,i,t。

(24)

8)运输能力约束

(25)

9)非负整数约束

fdnpijts,fdrpijts,afcits,xpit,ypit,vcit,zcit,

(26)

(3)第三层：分销中心

分销中心同样以最大化自身收益为运作目标，收入部分为新产品和再制造产品的销售总额，以及联合回收中心为回收产品支付的回购费用，成本部分为运输成本、回收成本、缺货成本、库存成本、产品进购费用的总和，表示为

sompjts)+SPRpjt·(DSMpjts-ssmpjts)+URCCpjt·

γpjts-USNPpjt·sompjts-USRPpjt·ssmpjts-

fdrpijts·tpbp)]。

(27)

同时，该层模型还应当满足下列约束:

1)新产品的库存平衡公式

(DOMpjts-sompjts),∀p,j,t,s。

(28)

2)再制造产品的库存平衡公式

·tpbp-(DSMpjts-ssmpjts),∀p,j,t,s。

(29)

3)回收产品的库存平衡公式

∀p,j,t,s。

(30)

4)回收产品数量约束

RPApjts-γpjts≥0,∀p,j,t,s。

(31)

5)缺货数量约束

DOMpjts-sompjts≥0,∀p,j,t,s;

(32)

DSMpjts-ssmpjts≥0,∀p,j,t,s。

(33)

6)库存能力约束

∀j,t,s;

(34)

(35)

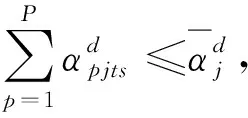
(36)

7)运输能力约束

∀j,t,s。

(37)

8)非负整数约束

sompjts,ssmpjts,dapjts,fdnpijts,

(38)

4 基于DCAGA的分层迭代求解方法

多层规划的求解一般都比较困难，对于简单的多层线性规划问题，一般可以找到反应函数的显性表达形式，并在此基础上进行求解。而在本文建立的回收—生产—分销协同计划模型中，各层决策变量虽然存在一定的内在联系，但是联系较为复杂且约束条件较多，很难直接求出显性反应函数。因此，本文采用分层迭代方法作为模型求解的整体策略，即从第一层开始依次向下一层迭代，同时设计DCAGA，将其应用于单次、单层模型求解，循环往复后获取协同计划问题的满意求解结果。

4.1 分层迭代方法描述

结合模型的结构和特点，分层迭代方法的具体步骤如下：

(1)生成初始变量 随机产生第三层模型中变量dapjts的初始解，需满足约束式(37)。

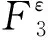
(6)循环计算 判断求解过程是否满足终止条件，若满足，则输出多层规划模型最优解的目标函数值及其相应的解集，不满足则再次循环转步骤(2)。

4.2 双倍体自适应遗传算法求解过程

在4.1节的分层迭代方法中，单次、单层的模型求解环节均采用了DCAGA。一方面，双倍体结构提供的记忆功能可以在交叉和变异过程中有效保留可用基因片段，改进收敛性能[22]；另一方面，引入的自适应公式可以实时调整交叉概率和变异概率，使其根据动态环境保持最佳取值，提高搜索性能。以单次生产模型的求解为例，设计如下关键技术步骤(第一、三层相似)：

(1)编码与解码

在双倍体结构中，每个完整的个体均由一条显性染色体和一条隐性染色体组成，每条染色体的编码和解码方式完全相同。

(2)构造适应度函数

本文采用适应性罚函数法，将搜索过程中获得的信息作为反馈来指导惩罚系数的调整，即惩罚系数ω(m+1)随进化代数的变化有以下3种更新方式：

(39)

式中：ϖ1>ϖ2>1，情况(1)表示过去m代中的最好个体均没有受到约束惩罚，情况(2)表示过去m代中的最好个体均受到了约束惩罚。利用自适应公式对惩罚系数进行调节，若当前最优个体均为可行解，则表明惩罚因子已经足够大，可适当降低对不可行解的惩罚压力；若当前最优个体均为不可行解，则需要适当增大对不可行解的惩罚。

(3)遗传操作

1)选择操作

采用轮盘赌方法进行选择操作。DCAGA是以显性染色体的适应度值作为个体选择概率的计算依据，并根据选择概率将整个个体，包括显性染色体和隐形染色体，复制到下一代种群中，其计算公式为

(40)

式中Pd为个体被选择的概率。该选择操作表明个体按照其对应的适应度值确定被选择和复制到下一代的概率，个体适应度值越高，其被选择的概率越大。

2)交叉操作

采用双点交叉操作对概率选中的染色体进行杂交，同时每代个体中显隐性染色体的自适应交叉概率

Pcr=

(41)

式中：Gavg为当前种群的平均适应度值；Gmax为当前种群的最大适应度值；Pcr1和Pcr2为式(41)的控制参数，一般取Pcr1=0.9，Pcr2=0.6。

3)变异操作

采用逆序操作对概率选中的染色体实施变异，同时每代个体中显隐性染色体的自适应变异概率

Pmu=

(42)

式中Pmu1和Pmu2为式(42)的控制参数，一般取Pmu1=0.1，Pmu2=0.001。

4)显隐性重排

当执行完选择、交叉、变异操作之后，需要重新计算每个个体中显性染色体和隐形染色体的适应度值，并根据适应度值的大小进行显隐性重排，即适应度值较大的染色体在新一轮遗传操作中将被设定为显性染色体，适应度较小的染色体被设定为隐形染色体。

5 仿真实例

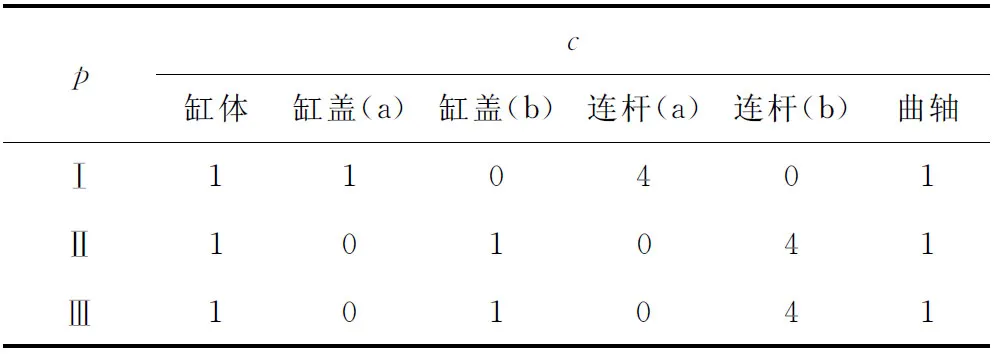
本章从某一汽车发动机生产供应网络获取基础数据样本，所考虑的三阶段闭环供应链系统中，除了一个联合回收中心，还有3个制造/再制造工厂(I=3)、5个分销中心(J=5)。以其中某一系列电喷式发动机作为上述协同计划模型和求解方法的应用对象。该系列产品主要包括3种不同型号的四缸电喷式发动机(P=3)，记为Ⅰ型、Ⅱ型、Ⅲ型。制造/再制造工厂可以针对发动机中的缸体总成、缸盖总成、连杆总成和曲轴总成进行再制造修复和生产。3种发动机的排量均为1.6 L，缸径均为81 mm，活塞行程均为77.4 mm，所用的材料都是铸铁缸体、全铝缸盖，发动机缸体和曲轴的曲拐尺寸均相同。Ⅱ型发动机和Ⅲ型发动机之间的核心组件可以相互交换使用，两者的主要不同之处是电控方案和进气管总成(可直接使用零部件)。而Ⅰ型发动机的连杆总成和缸盖总成与前两者不同，不能交换使用。因此，总共有6种不同的核心组件(C=6)，3种型号发动机p对核心组件c的物料系数BOCpc如表8所示。

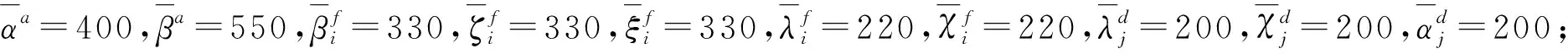
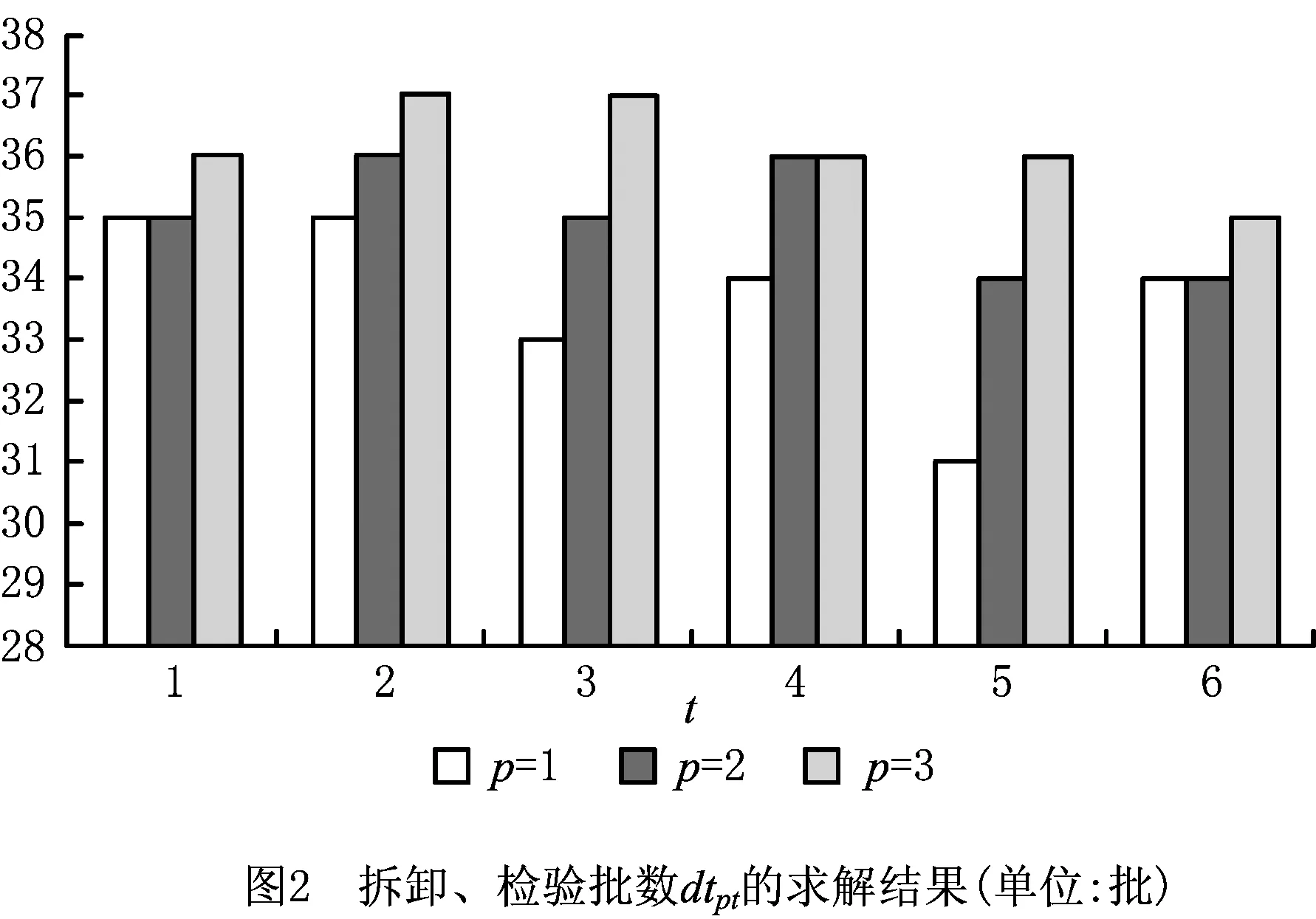
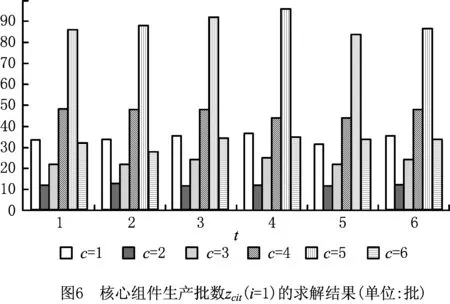
在仿真软件MATLAB 7.0上对上述模型和求解方法进行编译，并在CPU处理器为Core i7、内存为2 G、操作系统为Windows 7的笔记本电脑上运行。算法运行的参数为：pop_size=200，pop_gen=200，ω(0)=1/1 000，ϖ1=5，ϖ2=2，最大迭代次数为300。程序独立重复运行20次，得到最满意的计划方案。其中：拆卸、检验批数dtpt的求解结果如图2所示；核心组件生产批数vcit的求解结果如图3～图5所示；核心组件再生产批数zcit的求解结果如图6～图8所示；新产品装配批数xpit的求解结果如图9～图11所示；再制造产品装配批数ypit的求解结果如图12～图14所示(仅列出了部分关键变量的求解结果)。

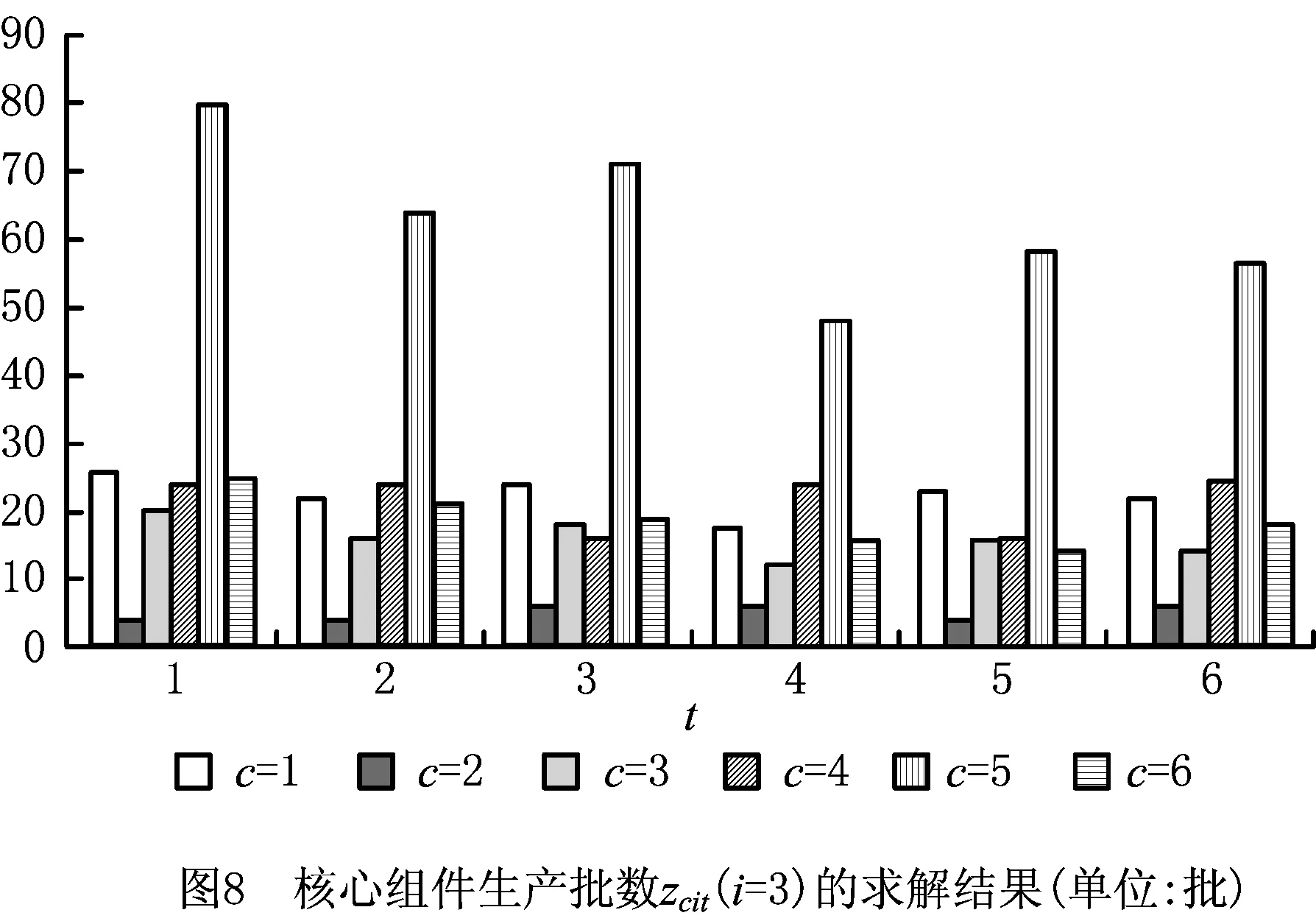
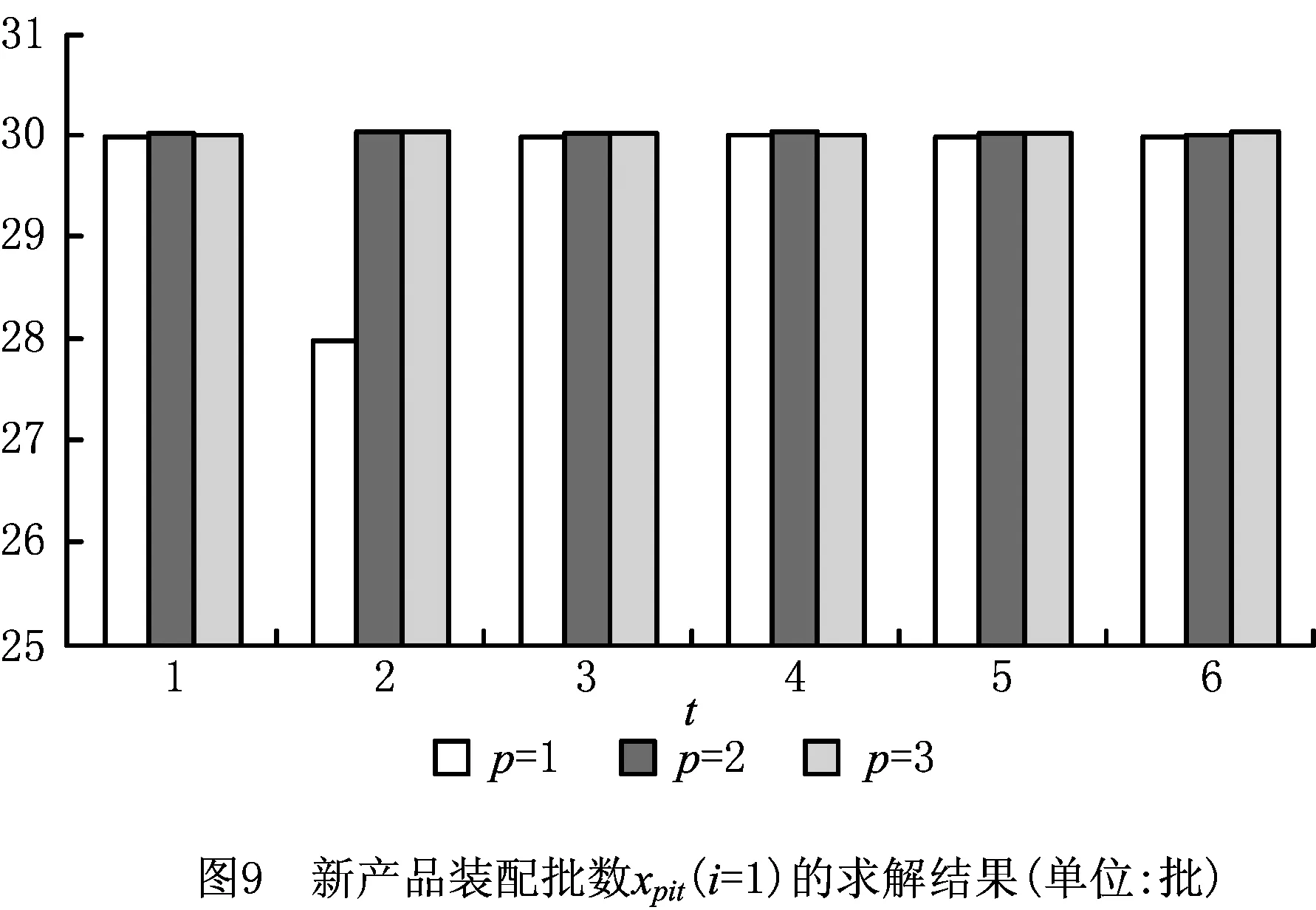
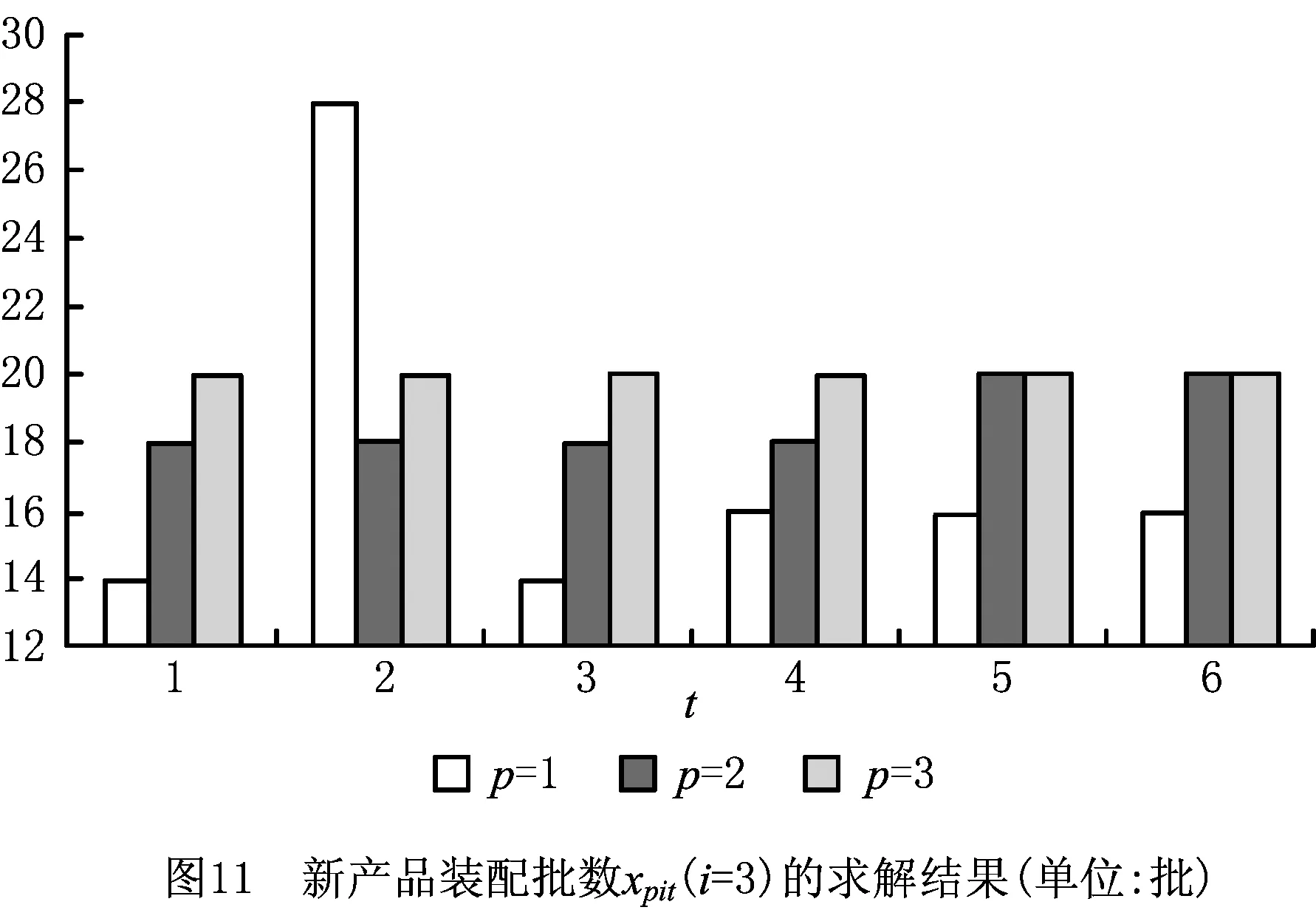
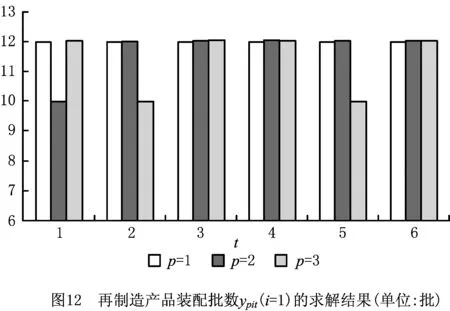
最满意求解结果表明，在规划周期内，联合回收中心盈利7 780 214 元；3个制造/再制造工厂分别盈利26 750 224 元、25 869 842 元、14 226 788 元，总体盈利66 846 854 元；5个分销中心分别盈利20 716 044元、19 252 228元、17 718 242元、18 866 324元、18 042 678元，总体盈利94 595 516；整个闭环供应链系统总收益为169 222 584元。从求解结果可以看出，本文所建立的协同计划模型，可以在市场需求和回收产品供应数量不确定环境下，实现闭环供应链各级成员企业的正、逆向运作活动的统一计划和协调：各个分销中心都能够积极地对处于生命周期末端的产品进行回收，并运往联合回收中心；联合回收中心能够根据不同的生产需求，将可用于再制造的核心组件运往各个制造/再制造工厂；每一个制造/再制造工厂根据分销中心下达的订货需求，合理安排新产品和再制造产品的生产；每一个分销中心可以自主选择新产品和再制造产品的供应渠道，并面向区域市场进行销售，最大限度地提升自身收益。

另一方面，按照独立制定运作计划的方式虽然可以获得局部收益的最大化，但是有可能影响其他成员企业的利益，甚至影响整个闭环供应链系统的协同运作绩效。例如，若联合回收中心独立制定运作计划，则可使其自身收益达到9 028 572 元，但此时制造/再制造工厂的总体盈利最多可达51 542 208 元，分销中心的总体盈利最多可达85 103 256 元，整个闭环供应链系统总收益仅为145 674 036 元。因此，本文建立的模型和相应设计的求解过程，不但能够比较准确地描述闭环供应链中不同成员企业之间的正、逆向运作活动，而且在决策信息不断循环交互的过程中，可以实现各级成员都满意的运作目标，确保各级成员之间、各级成员与整体系统之间的利益平衡。

6 结束语

本文在闭环供应链系统的协同计划研究方面做了一些尝试，针对由一个联合回收中心、多个制造/再制造工厂和多个分销中心组成的三阶段闭环供应链网络，在市场需求和回收产品供应数量不确定性影响的条件下，建立了回收—生产—分销三层协同计划模型。结合模型特点设计了分层迭代整体求解策略，并在单层求解过程中设计了双倍体自适应遗传算法，利用双倍体结构和自适应公式提升求解效率。所设计的模型和求解方法，不但能够实现闭环供应链各级成员企业正、逆向运作活动的统一计划和协调，而且可以确保各级成员之间、各级成员与整体系统之间的利益平衡。最后，通过仿真实例验证了所述模型和求解方法的适用性和有效性。