单失效数据情形下蓄能器可靠性评估

郭 锐 张荣兵 赵静一 ，4 汪晋锋

1.燕山大学河北省重型机械流体动力传输与控制重点实验室，秦皇岛，066004

2.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

3.燕山大学机械工程学院，秦皇岛，066004

4.秦皇岛燕大一华机电工程技术研究院有限公司，秦皇岛，066004

0 引言

隔膜式蓄能器采用密封的钢制外壳和橡胶隔膜将蓄能器分为两部分，分别充入氮气和液压油。隔膜式蓄能器利用橡胶隔膜的移动和气体的可压缩性对受压液体的能量进行储存和释放，广泛用于紧急或快速能量储存、吸收液压管路冲击、吸收液压泵的流量脉动、泄漏补偿、液气弹簧及不同液体的传输等，是液压系统中不可或缺的辅助装置，其可靠性直接关系到整个系统的稳定性。

景涛等［1］提出了一种基于核主元分析和模糊支持向量机的可靠性寿命分布模型识别方法。胡志威［2］研究了全水润滑斜轴式海水柱塞泵的可靠性，通过绘制P⁃S⁃N曲线，对其连杆进行了疲劳寿命的可靠性研究。戴城国等［3］提出用模糊综合评判的方法对电液伺服阀FM ECA进行改进，通过建立因素集、评价集和权重集等步骤实施模糊综合评判，得到评判结果，给出了电液伺服阀各故障模式对整个伺服阀系统的危害度等级。王帅等［4］提出了一种可定量预估管路结构在多种试验环境下随机振动疲劳损伤的分析方法。陈东宁等［5］综合考虑液压冲击、温度、压力及弯曲半径等因素的影响，设计了液压软管总成可靠性试验台，求得液压软管总成在脉冲、爆破试验条件下的平均寿命、可靠寿命、可靠度的点估计及置信下限。冷景平等［6］研究开发了蓄能器疲劳试验系统，实现同时对两个蓄能器进行疲劳试验。杨国安等［7］对钻井泵阀疲劳寿命进行研究，依据泵阀疲劳寿命曲线对泵阀使用寿命进行估算。褚渊博等［8］建立了射流管式伺服阀喷嘴至接收器部位的可视化仿真模型并进行了冲蚀磨损率的数值模拟和理论寿命的计算。JIANG等［9］研究了液压泵在变转速下提取故障特征的问题，提出了基于阶次跟踪的诊断方法。NAZIR等［10］针对液压伺服系统的非线性因素，根据进化算法的性能指标，提出了一种预测优化算法可靠性的新技术，可统计认证优化的有效性和鲁棒性。GUO等［11］提出了基于液压泵小样本可靠性试验的寿命预测和试验期优化模型，提出了液压泵小样本可靠性测试的循环约束优化搜索策略，解决了测试采样周期和紧缩端阈值优化问题，并验证了最小采样周期的精度。苗学问等［12］提出了一种用于飞机发动机轴承的GL预测模型支持向量机（sup⁃port vectormachine，SVM）。

蓄能器是高可靠长寿命元件，试验周期长，费用高，结合前人研究经验，采用小样本进行试验显得很重要。元件处于故障率的浴盆曲线中段时，需要大量时间才会出现失效，或者无失效。这种情况下，针对隔膜式蓄能器的单失效或无失效数据的研究具有十分重要的意义。

茆诗松等［13］提出在极少失效数据情况下进行可靠性评估，运用传统的可靠性评估方法处理极少失效数据时，处理结果偏差较大，这是由于传统的可靠性评估方法通常需要较多的失效数据进行处理。在单失效情况下，傅惠民等［14］假设已知威布尔分布的形状参数，能得到特定时间内可靠度的置信区间。张志华［15］、陈文华等［16］在单失效情况下，运用配分布曲线法对威布尔分布和正态分布进行参数估计，得到了参数的点估计。徐宝等［17］用参数估计方法研究了寿命服从Pascal分布的产品可靠度在只有一个数据失效情况下的Bayes估计问题，对于给定的Beta先验分布，得到了可靠度的多层Bayes估计以及E⁃Bayes估计的形式。

以上研究均未涉及蓄能器试验领域，本文引入蓄能器相关理论，设计小样本量下的蓄能器疲劳寿命可靠性试验，采用无替换定时截尾的方法得到单失效数据，利用单失效数据分析对其进行可靠性研究，分别得到指数分布和威布尔分布场合下蓄能器的可靠性及寿命评估。

1 单失效数据指数分布和威布尔分布情形下的可靠性评估

在与机械产品相关的可靠性试验中，指数分布和威布尔分布得到较为广泛的应用。隔膜式蓄能器是一个整体机械结构，组成隔膜式蓄能器的零部件很多，常见的故障形式有隔膜破裂和上下壳体密封破坏等，可以认为都是因为其中的零部件失效，从而证明组成隔膜式蓄能器的薄弱易损的零部件决定着隔膜式蓄能器的寿命。所以隔膜式蓄能器的寿命分布服从指数分布或者威布尔分布是合理的。假定隔膜式蓄能器寿命分布服从二参数威布尔分布，即位置参数γ=0。

1.1 单失效数据指数分布的可靠性分析

张忠占等［18］对产品可靠性试验数据进行统计分析时发现，如果产品发生失效的个数r≥2时，有很多统计分析的成熟方法可以选择。但由于产品可靠性水平的不断提高，在对产品进行可靠性试验时，即使对产品进行加速寿命试验，也往往在试验结束时发现被测产品出现无失效或者单失效的情况，这种情况特别容易在小样本测试中出现。虽然很多学者和专家对无失效数据的统计分析进行了研究，并且提出了很多方法和理论，但是对单失效数据的可靠性统计分析的方法却是少之又少。为了充分利用各种失效数据来提高可靠性指标估计的准确度，需要对单失效数据的可靠性分析方法进行研究，并且以相关的试验为基础来验证提出的单失效数据的可靠性分析方法。

评定隔膜式蓄能器的可靠性，对隔膜式蓄能器进行m次定时截尾寿命试验，截尾时间分别为t1,t2,…,tm，其中，t1＜t2＜…＜tm，对应的测试样品数量分别是n1,n2,…,nm。在整个可靠性试验过程中，所有被测试的样品中只有一个样品发生失效。由于隔膜式蓄能器的可靠性较高，故通常在(tm-1,tm)区间发生失效。则隔膜式蓄能器单失效数据能够表示为(ni,ti)，i=1,2,…,m，此时引入失效时间ts来进行可靠性分析。

1.1.1 先验分布的确定

假设隔膜式蓄能器的寿命t服从指数分布，其分布函数为

式中，λ为失效率；t＞0。

如果共轭伽马（a，b）分布是λ的先验分布，则其密度函数为

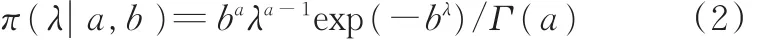
其中，Γ(a)为伽马函数，并且a＞0,b＞0；a和b是超参数。在单失效数据情况下，需要选取a和b的值，使π(λ|a,b)为λ的减函数。当0＜a≤1和b＞ 0时，有dπ(λ|a,b)/dλ，从而π(λ|a,b)为λ的减函数。由贝叶斯估计的稳定性可知，先验分布尾部越细，贝叶斯估计的稳健性越差，所以0＜a≤1时，b最好不取太大值，假设c为b的上限，专家能根据经验来确定c的取值，这时将a和b的范围调整为0＜a≤1，0＜b＜c。

根据多层先验分布的相关知识，b的先验分布可以在(0,c)上均匀分布，其密度函数为

此时λ的多层先验分布的密度函数为

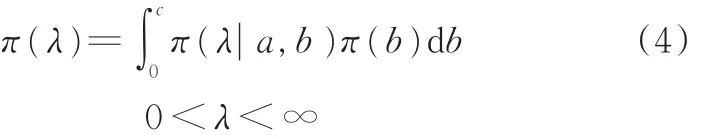
1.1.2 失效概率的贝叶斯估计

本文主要研究a=1时λ的多层贝叶斯估计：

式（5）还是关于λ的减函数。由于隔膜式蓄能器可靠性高，在之前的m-1次定时截尾试验中没有产生失效数据，在这种情况下，失效率λ的多层贝叶斯估计［19］

由定理可知，在隔膜式蓄能器寿命分布服从指数分布进行的m次定时截尾试验中，最后只有一个隔膜式蓄能器在ts时失效，其中，ts∈(tm-1,tm)。此时得到的单失效数据为(ni,ti)，i=1,2,…,m。如果λ的多层先验密度函数π(λ)由式（5）给出，则在平方损失下λ的多层贝叶斯估计

式（7）的证明如下：对寿命分布服从指数分布的隔膜式蓄能器进行m次定时截尾试验，如果在最后一次试验中有一个被测样品发生失效，则有

式中，P1,P2,…,Pm分别为隔膜式蓄能器进行1，2，…，m次定时截尾试验时的失效概率；Tim为进行第m次截尾试验时有i个被测样品发生失效时的失效时间。

其似然函数为

如果π(λ)由式（5）给出，则根据贝叶斯定理，可以得到λ的多层后验密度函数：

结合之前m-1次定时截尾试验记录的无失效试验数据和最后一次定时截尾获得的一个失效数据，得到失效率λ的加权Bayes估计［20］：

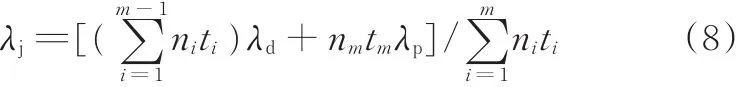
1.1.3 可靠度估计

可靠度Rg的计算公式为

1.2 单失效数据威布尔分布的可靠性分析

1.2.1 单失效数据模型

假设采用n个试验样品进行定时截尾试验，τ1,τ2,…,τk分别为定时截尾的时间，0＜ τ1＜τ2＜…＜τk。如果在试验过程中，时间段(τm-1,τm)内有一个试验样品失效（其中1≤m＜k），就可得到单失效数据的模型，记作（si,ri,τi），τi时刻参加测试的样品数量和产生失效的样品数量分别用si、ri表示。所以i≤m-1时，失效数ri=0；i＞m-1时，ri=1，同时参加测试的样本数量需满足s1≥s2≥…≥sk。综上所述，可得：①当τ0=0时，失效概率p0=0。②由于0＜τ1＜τ2＜ …＜ τk，记 作 pi=P(T ＜ τi)，则 有 p1＜p2＜ …＜ pk，当sk较大时，pi(i=1,2,…,k)较小。③因为在(τm-1,τm)内有测试样品失效，故可知一些产品的寿命低于τm。

1.2.2 单失效数据下的贝叶斯估计

贝叶斯估计方法是根据所得数据的特点，首先假设失效概率pi服从某种形式的先验分布，之后根据条件概率的思想，采用似然函数，得到失效概率pi的后验分布，最后得到失效概率pi的估计值。通常而言，贝叶斯估计方法性能较好，但如果选择了不适合的失效概率pi的先验分布，那么贝叶斯估计方法的使用效果会非常差，所以，为贝叶斯估计方法选择合适的失效概率pi的先验分布是非常重要的。

（1）先验分布的确立。假设产品在内的可靠度很高，即失效概率pi较小的可能性很大。不完全β分布B(θ1,θ2,a,b)的密度函数为

当a，b取值一定时，式（10）是关于失效概率pi的单调减函数。

当出现单失效数据时（即当i＞m-1时），采用不完全β分布B(θ1,θ2,a,b)作为失效概率pi的先验分布，可能导致一个试验样品发生过失效这样的信息丢失，但是通过调整失效概率pi的取值下限可以有效解决此问题。所以，在单失效数据情况下也能采用不完全β分布B(θ1,θ2,a,b)作为失效概率pi的先验分布。

（2）超参数的选取问题。当式（10）中a≤1、b＞1时，此时该函数是关于失效概率pi的单调减函数，这满足了失效概率pi的值较小的可能性很大的先验信息。由此a≤1、b＞1为超参数a和b大概的取值范围。当b为固定值、a≤1时，随着a的减小，密度函数曲线右侧尾部会越来越细［21］。由贝叶斯估计的稳定性可知，先验分布尾部越细，贝叶斯估计的稳健性越差。因此，确定超参数a的取值为1。

通常先设定好超参数b的取值上限C，在[1,C]内均匀地取值，这时可以认为超参数b是服从区间[1,C]上的二级先验分布，即

πi2(b)=U(1,C) （11）

用U(α,β)表示在[α,β]上的均匀分布，C为常数。考虑不完全β分布密度函数性质，当a=1时，选取的超参数b越大，密度函数曲线右侧尾部越细。同时考虑到先验分布尾部越细会导致贝叶斯估计的稳健性变差这一问题，超参数b的上限值C不宜太大，通常选取3～7最好［22］（本文选取C等于5或6进行计算）。

由式（10）可以得到失效概率pi的一级先验分布式：

根据贝叶斯定理，可以得到失效概率pi的先验分布式：

由式（13）可以看出，它是关于失效概率pi的单调减函数。

（3）失效概率的贝叶斯估计。假设在定时截尾时间τi内，对si个试验样本进行试验，且有ri个试验样本发生失效，其似然函数为

当i＜m，ri=0时，可靠性试验是在无失效数据的情况下进行的，此时需要用无失效数据贝叶斯估计方法对失效概率pi进行估计，其似然函数为

在平方损失函数下用式（13）作为失效概率pi的先验分布的贝叶斯估计，即

当i≥m时，ri=1，即有一个试验样本在试验中产生失效，由式（14）可得到其似然函数：

假设试验样本在τα(m-1＜α＜m)内产生失效，通常而言，失效现象的产生是随机性的，所以根据博弈理论，τα时的失效概率pα=max(pe,m-1,0.5)是合理的。通过不完全β分布B(pα,1,1,b)可以得到pm的先验分布：

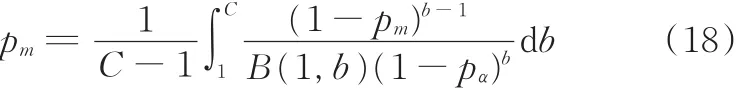
显然式（18）是单调递减函数，则以其作为pm的先验分布是正确的。

在平方损失函数下，以式（18）作为失效概率pm的先验分布的贝叶斯估计，即其后验分布

Dm=1-pαEm=(C-1)pα

Fm=sm+C Gm=ln(Fm/(sm+1))

得到pm的贝叶斯估计值pe,m后，即可再次利用类似无失效数据的贝叶斯估计方法，在平方损失函数下，得到单失效数据下pi(i＞m)的多层贝叶斯估计：

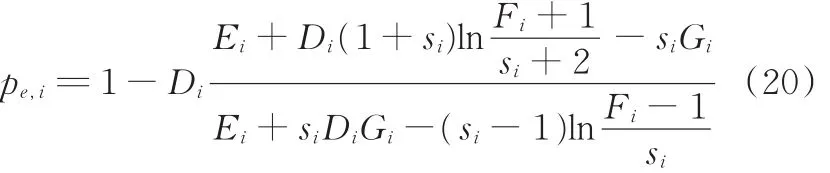
1.2.3 可靠性分布参数以及特征值的估计

得到各个时刻的失效概率pi=P(t＞τi)的贝叶斯估计值后，就可以用加权最小二乘法对试验样本的威布尔分布中的分布参数和特征值进行估计。假设隔膜式蓄能器的寿命T服从两参数威布尔分布，其表达式

式中，m为形状参数，m＞1；η为特征寿命，η＞0。

式中，wi为权系数。

得到形状参数m和特征寿命η的估计值后就可以进行可靠度函数、失效概率密度函数和失效率函数的计算。可靠度函数为

2 蓄能器试验

蓄能器可靠性试验是疲劳寿命试验，是蓄能器型式试验的一项重要内容。测试的蓄能器是隔膜式的，属于隔离式蓄能器的范畴。相关标准主要有JB/T 7037-2006《液压隔离式蓄能器试验方法》和JB/T 7034-2006《液压隔膜式蓄能器型式和尺寸》等。本文设计了一种节能、高效的蓄能器疲劳试验系统来进行蓄能器可靠性试验。

2.1 试验系统及方案设计

根据蓄能器可靠性试验要求，设计了蓄能器试验液压系统，系统原理见图1。

蓄能器可靠性试验台液压系统主要由主液压泵、主电动机、过滤装置、蓄能器和各个液压阀等组成，实现了对被测蓄能器进行反复充放液动作并检测相关信号的功能。疲劳寿命试验台的主要特点是可以同时对2组被测蓄能器进行疲劳测试试验，节约了成本和时间。隔膜式蓄能器进行可靠性试验的现场情况见图2。

图1 液压系统原理Fig.1 Schem atic d iagram of hyd raulic system

图2 可靠性试验台现场Fig.2 Site diagram of reliability test station

2.2 被试样本及其压力容积匹配

本蓄能器可靠性试验方案采用的被测样本是GXQ⁃C⁃2/25⁃M⁃Y型蓄能器，其结构见图3。

图3 隔膜式蓄能器结构Fig.3 Structure of diaphragm type accumu lator

蓄能器内有气体压缩与膨胀现象发生，根据波意尔-马瑞特定律，理想气体状态变化关系为

式中，p0为预充气体压力；V0为压力在p0时的预充气体体积；p1为最小工作压力；V1为压力在p1时的气体体积；p2为最大工作压力；V2为压力在p2时的气体体积；n为多变指数。

压力容积的p⁃V关系见图4。

图4 蓄能器压力容积p-V图Fig.4 Pressure volume PV diagram of accumu lator

2.3 试验方案的选择

蓄能器可靠性试验采用无替换定时截尾试验。根据相关经验，选取120～1 680 h为截止时间，试验充放频率为每6 s进行一次充放液，即认为选取7.2万～100.8万次为截止时间，每天试验12 h，则100.8万次需要大概140天（即3 360 h）。

2.4 试验数据的采集

对于隔膜式蓄能器可靠性寿命试验，首先应确定其失效判据，见表1。

表1 蓄能器失效依据Tab.1 Failure basisof accumu lator

蓄能器可靠性试验数据是测试数据，测试样品是在企业的成品库中随机抽取的，20个试验样品按每10个为一组进行试验，试验过程中，要注意对压力传感器的显示值和测试样本的情况进行观察。在917 h（即55万次）时，一样品发生故障失效，失效形式为隔膜式蓄能器上下壳体密封破坏出现油喷，见图5，此时采集到的压力试验曲线见图6。记录隔膜式蓄能器发生失效的时间和相应的定时截尾时间，定时截尾时间和得到的蓄能器可靠性试验单失效数据见表2。

图5 隔膜式蓄能器壳体密封破坏Fig.5 Seal failu re of diaphragm accum ulator shell

图6 隔膜式蓄能器发生失效时压力试验曲线Fig.6 Pressure test curve of diaphragm accum u lator failu re

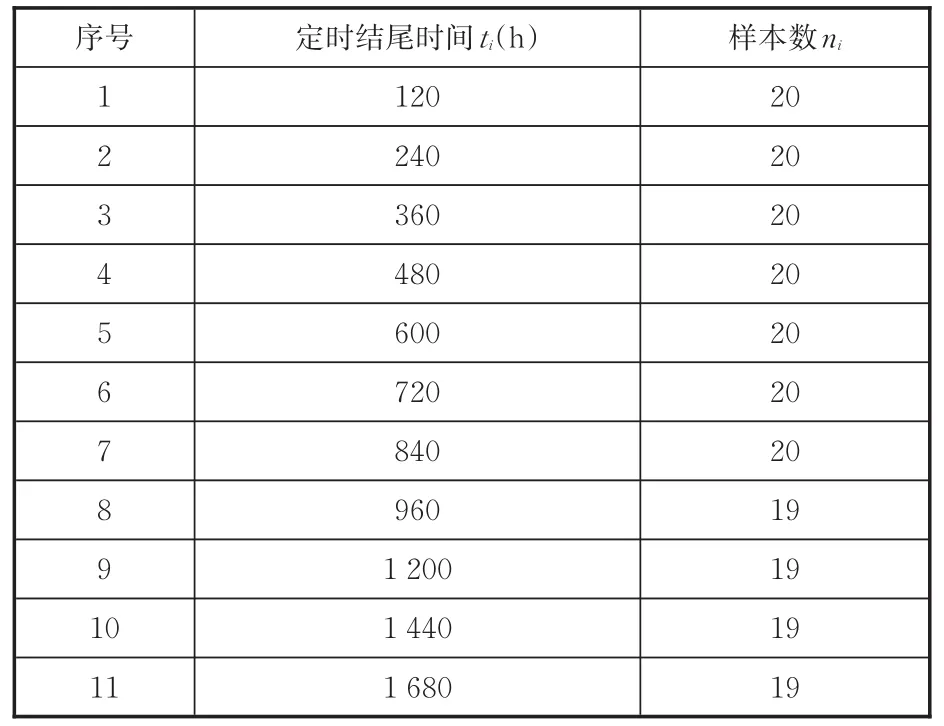
表2 蓄能器定时单失效试验数据Tab.2 Test data of accum u lator failu re tim e

指数分布下单失效数据处理流程见图7。

2.5 单失效数据情形下指数分布试验分析

由上文中定理可知，失效率λ的贝叶斯估计与M有关，而M与失效时间和截止时间有关，这符合实际情况。将表2中序号1～8的数据代入式（8），得到λj的估计，见表3。由表3的计算结果可以得到1 000 h时可靠度的贝叶斯估计，见表4。可以发现，对于不同的 C（C=100，500，1 000，2 000，3 000），可靠度的贝叶斯估计结果比较稳健。

表3 λj的估计Tab.3 Estim ation ofλj

表4 可靠度的估计Tab.4 Estim ation of reliability

由式（9）得到隔膜式蓄能器指数分布寿命曲线（图8）。当C分别为100，500，1 000，2 000，3 000时，可靠度函数基本重合，较为直观地反映出可靠度的贝叶斯估计结果比较稳健。但由横坐标时间过大可知，隔膜式蓄能器指数分布的寿命预测不是很贴合实际，需要慎重使用。

图8 隔膜式蓄能器指数分布寿命曲线Fig.8 Exponen tial d istribution life cu rve of diaph ragm accum ulator

2.6 单失效数据情形下威布尔分布试验分析

威布尔分布下单失效数据处理流程见图9。将表2中单失效数据进行整理，见表5。

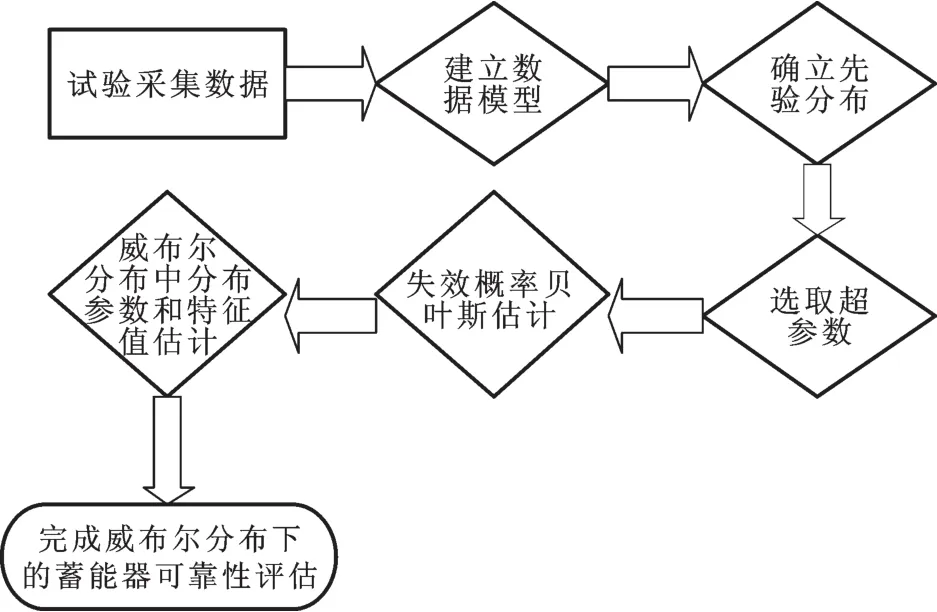
表5 蓄能器定时单失效试验数据Tab.5 Test data of accum u lator failure time

当C为5或6时，分别将表5中的数据代入计算式中，可以得到相应的pi，见表6。

表6 pi估计值Tab.6 Estimate of pi

结合表6中相关数据和式（21）可得：当C=5时，me=2.040 867 3，ηe=1 488.277 8；当C=6时，me=2.059 759，ηe=1 489.548。

由双参数威布尔分布可靠度模型，根据贝叶斯方法计算得到蓄能器寿命可靠度模型，得到的可靠度函数见图10。

可以看出，C=5和C=6时的可靠度函数曲线基本重合，可知C的小范围取值对可靠度的影响不大。当C=5时，得到了失效概率密度函数（图11）：

图10 可靠度函数Fig.10 Reliability function

图11 失效概率密度函数Fig.11 Failure probability density function

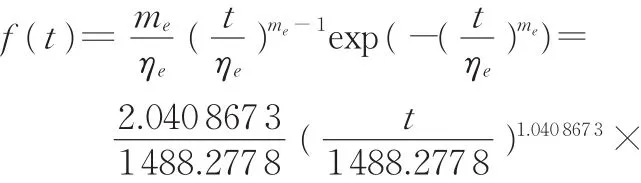
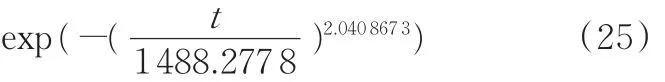
当C=5时，得到了失效率函数（图12）：

图12 失效率函数Fig.12 Failure rate function

3 结论

（1）本文应用并行节能理论，设计了能够同时对20个样本进行试验的新型多蓄能器可靠性节能试验装置。

（2）采用无替换定时截尾的方法得到单失效数据，利用单失效数据分析对其进行可靠性研究，在指数分布和威布尔分布场合下对蓄能器进行可靠性及寿命评估。通过指数分布对隔膜式蓄能器的可靠性寿命进行分析可以发现，它有一定的使用基础，但是由于在出现失效数据情况下就停止试验而进行数据分析，忽略了之后进行试验时所得到的数据对可靠性分析的影响；采用威布尔分布对单失效数据进行可靠性评估，综合考虑了失效前、失效时和失效后实验数据对可靠性评估的影响，认为威布尔分布对蓄能器可靠性评估更具有理论和工程意义。

（3）被测试样本GXQ⁃C⁃2/25⁃M⁃Y型隔膜式蓄能器应用在工程机械、矿山机械中，可靠性满足工程应用要求，有效吸收了机械振动产生的压力脉动，从而避免液压系统管路和元件受到损坏，延长了设备使用寿命。