基于混合灰狼算法实现第Ⅱ类机器人U型装配线能耗优化

张子凯 唐秋华 张利平 李梓响

1.武汉科技大学冶金装备及其控制教育部重点实验室，武汉，430081

2.武汉科技大学机械传动与制造工程湖北省重点实验室，武汉，430081

0 引言

装配线是一种常用于汽车、电子等行业的产品制造系统。在装配线上，产品从入口线的工位依次进入下一工位进行装配，直到从出口线的工位出来。该过程中，工序的装配顺序需满足工序间的优先关系，且工位的加工时间应小于节拍。不同于传统的直线型装配线，U型装配线的同一工位既可以包含入口线工序，也可以包含出口线工序，这使得U型装配线具有更高的生产效率和柔性。如今，自动化技术已逐渐应用到企业的装配系统，机器人开始逐渐替代工人在装配线上进行作业的装配。

M ILTENBURC等［1］提出并构建了U型装配线平衡的数学模型后，众多学者开始研究U型装配线平衡问题。GÖKÇEN等［2］采用最短路径法、OGAN等［3］提出分支定界法来求解简单U型装配线平衡问题。LI等［4］提出多规则启发式算法求解第二类U型装配线平衡问题。RABBBANI等［5］同时考虑混流U型装配线的工位负载和线效率，提出了基于规则编码的遗传算法来实现该类问题的求解。张子凯等［6］设计了基于Bender分解的多目标快速非支配遗传算法来实现多重资源约束下的第一类U型装配线平衡问题的求解。查靓等［7］运用基于信息素更新的蚁群算法求解第一类U型装配线问题。刘冉等［8］采用多目标克隆免疫协同进化算法来实现混流U型装配线平衡与调度的多目标集成优化问题的求解。唐秋华等［9］基于随机机会约束规划，通过确定性等价和线性化处理模型，采用GAMS/Cplex实现小规模U型装配线的平衡问题的优化。

总体来看，上述研究主要是研究半自动化或人工U型装配线，主要目的是在生产节拍和优先关系的约束下，将各装配工序分配到工位。不同于该类装配线，机器人装配线不仅要分配工序到工位，还应当分配机器人到工位。因此为实现机器人U型装配线工序和机器的协同优化，本文以能耗为优化目标，提出一种基于随机键编码的混合灰狼优化（hybrid gray w olf optim ization，HG⁃WO）算法，并将算法与原始灰狼算法进行对比以证明算法的优越性。

1 机器人U型装配线

机器人U型装配线由若干个工作站组成，每个工作站一般配备一个机器人来完成装配工序，因此，机器人U型装配线问题主要涉及两类问题：工序分配和机器人分配。

U型装配线中，某一工序的直接前序或直接后序分配到工作站，该工序才能进行分配。为描述这种关系，URBAN［10］提出了影子优先约束关系（图1）。基于影子优先约束关系分配工序到工作站时，每个工作站的装配时间应当小于或等于预定的节拍。

图1 影子优先约束关系Fig.1 Phantom p recedence relationship

分配机器人到工作站时，一般假设机器人的数量等于工作站的数量，且各工序在不同机器人上的装配时间不同［11］。由于部分机器人不能装配所有的工序，故当某一机器人无法装配某一工序时，设置其装配时间为一个极大值。图2展示了机器人U型装配线。

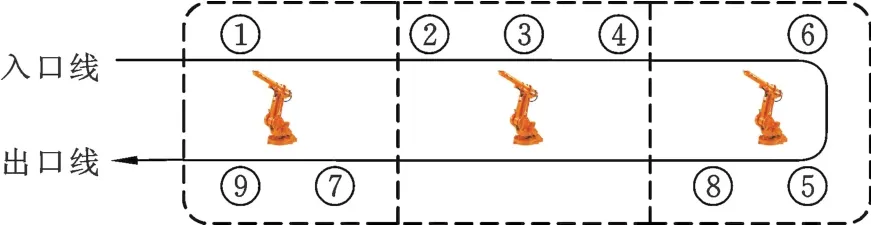
机器人装配线平衡问题中，一般以能耗为其主要的优化目标。装配线问题中，能耗特指电能耗，主要包含两部分：装配能耗和待机能耗。各能耗分别与装配时间和待机时间成正比［12］，计算公式如下：

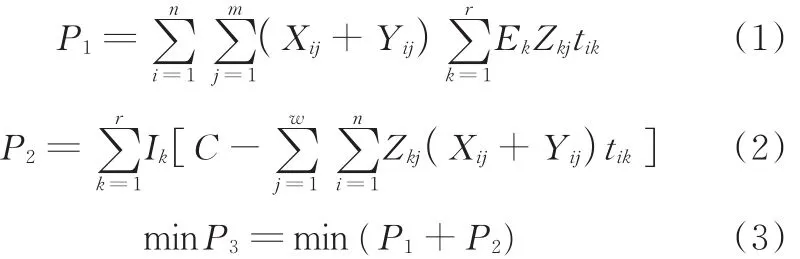
式中，P1为装配能耗；P2为待机能耗；P3为总能耗；n、m、r分别为工序数、工作站数和机器数；Xij(Yij)为1表示工序i分配到工作站j的入口线（出口线）；Zkj为1表示机器人k分配到工作站j；tik为工序i在机器人k上的装配时间；Ek、Ik分别为机器人k的装配单元能耗和待机单元能耗；C为节拍。

2 混合灰狼算法

原始的灰狼算法模拟灰狼寻找猎物的行为来搜索最优解。灰狼社会有4种狼：α、β、δ和ω，其中，具有最佳适应度的狼称为α，具有第二、第三最佳适应度的狼分别称为β和δ，其余的狼称为ω。灰狼算法中，低等级的狼必须服从高等级的狼，所以算法中的狩猎过程（优化过程）主要由α、β和δ引导ω包围猎物，并不断更新其位置，更新方式如下：

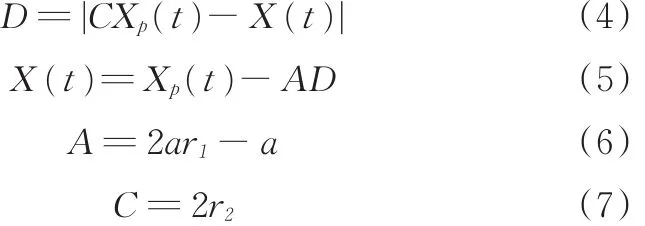
式中，t为当前迭代次数；Xp为猎物位置；X为灰狼的位置；A、C为系数；r1、r2为服从［0，1］均匀分布的随机变量；a在迭代过程中，从2到0线性下降。

在α、β和δ引导ω包围猎物时，由于猎物的位置是未知的，该算法假设猎物位于α、β和δ之间，所以在α、β和δ引导下，灰狼ω位置更新如下：

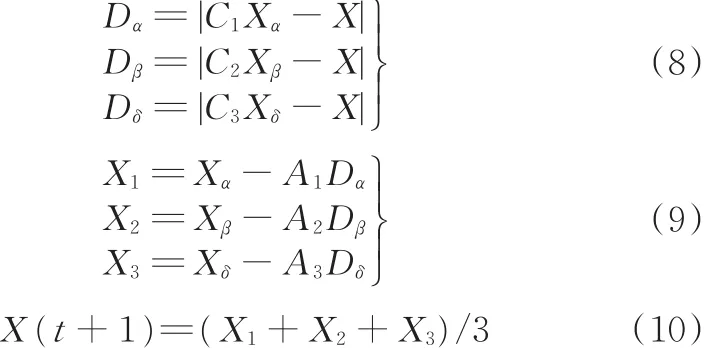
其中，Xα、Xβ、Xδ分别为α、β和δ的位置。

上述灰狼算法常用来处理连续问题，而机器人U型装配线为一个离散问题。为此，有效的编码方式和进化机制是实现灰狼算法求解机器人U型装配线平衡问题的关键。本文提出的混合灰狼算法采用随机键编码方式对种群个体进行编码，解码中，考虑工序间的优先关系约束和节拍约束，将工序和机器人分配到工位，计算灰狼的适应度函数值（能耗值）。算法基于灰狼个体间的社会等级信息，选择出3只最优狼指引剩余个体进化，防止算法陷入局部最优，以实现种群的更新。最后，算法采用交叉算子，以实现种群间的信息交流。

2.1 编码和解码

机器人U型装配线涉及工序和机器人的分配［13⁃15］，因此，种群初始化时，其编码主要包含两部分：工序编码和机器人编码。

工序编码采用随机键编码方式，以实现连续问题到离散问题的转换。该编码包含N个要素，每一个要素为0、1之间的随机数，且每一位置的随机数表示对应工序的权值。当从可选工序集中选择工序进行分配时，权值最大的工序被挑选出来。可选工序集包含两部分：入口线可选工序集和出口线可选工序集。依据影子优先约束关系，若工序的所有直接前序工序已分配，则该工序进入入口线可选工序集；若工序的所有直接后续工序已分配，则进入出口线可选工序集。

如图3所示，某一灰狼的工序权值编码为{0.910 1，0.854 2，0.321 5，0.120 3，0.146 5，0.652 4，0.854 1，0.941 2，0.215 3}。由影子优先约束关系图（图1）可知，初始入口线可选工序集为{1}，出口线可选工序集为{7，9}，则可选工序集中具有最大权值0.910 1的工序1被挑选出，存放到工序分配序列第一个位置，且被分配到入口线。由于工序1已被分配，则工序1从可选工序集中剔除，且此时工序2、3、4的所有直接前序工序1已被分配，则工序2、3、4进入入口线可选工序集。更新后，入口线可选工序集为{2，3，4}，出口线可选工序集为{7，9}。第二次选择时，可选工序集中具有最大权值0.852 4的工序2存放到工序分配序列第二个位置，且被分配到入口线。以此类推，直到所有的工序存放到工序分配序列。机器人编码中，编码长度等于工位的数量且每一要素表示机器人代号。

上述工序编码和机器编码仅仅得到工序分配顺序和机器人分配情况，而解码方式则是进一步获取工序分配到工位情况以及获取适应度函数值。具体步骤如下：

（1）初始节拍值为

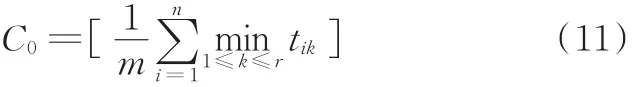
令当前节拍C=C0，工作站序号j=1；

（2）按照工序分配序列，将工序i分配到工作站j中，若分配后的工作站装配时间大于节拍C，则工作站序号j←j+1，将工序i重新分配到工作站j；

（3）重复步骤（2），直至工序全部分配；

（4）若工作站数量大于m，则令C←C+1，转步骤（2）；

（5）计算能耗值。

2.2 进化机制

根据原始灰狼算法包围猎物的原理，利用适应度函数最佳的3只灰狼α、β和δ引导其余灰狼ω包围猎物，实现位置的更新。

2.3 交叉算子

原始灰狼算法只有最佳的3只灰狼α、β、δ与其余灰狼ω存在信息交流，最低等级的灰狼ω之间无信息交流。因此，为增强灰狼间的信息交流，该算法分别针对工序编码和机器人编码，提出两种交叉方式：双点工序交叉和单点机器人交叉。具体交叉方式如图4、图5所示。

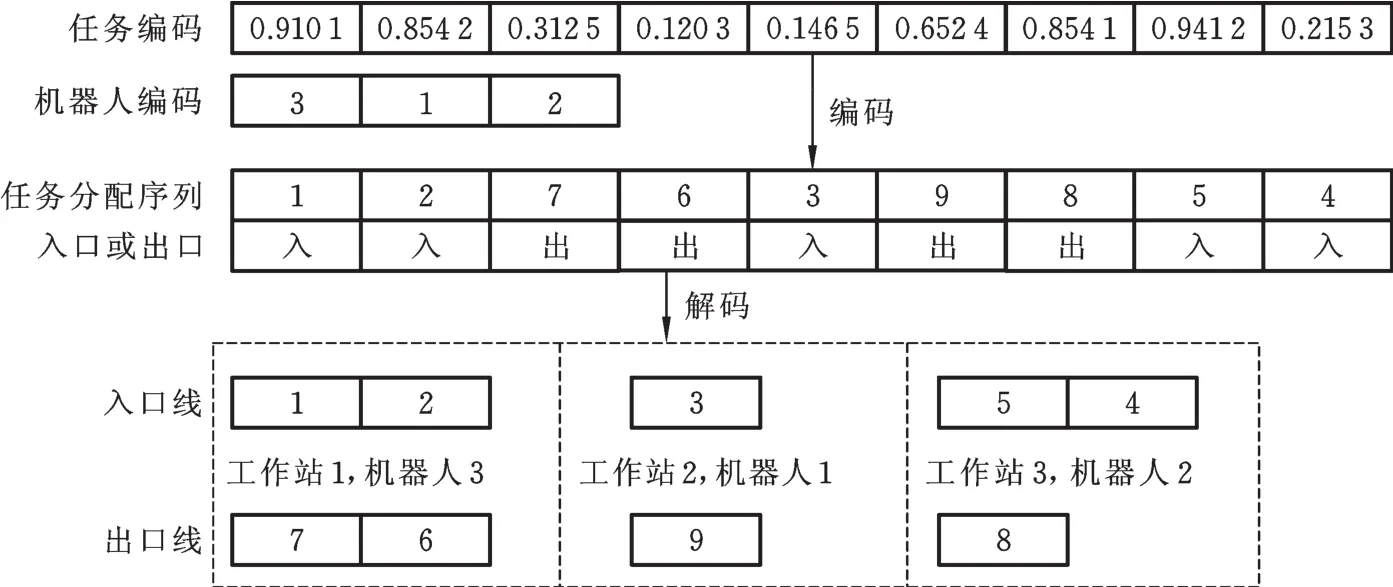
图3 编码和解码Fig.3 Encode and decode

图4 双点工序交叉Fig.4 Two-point task crossover

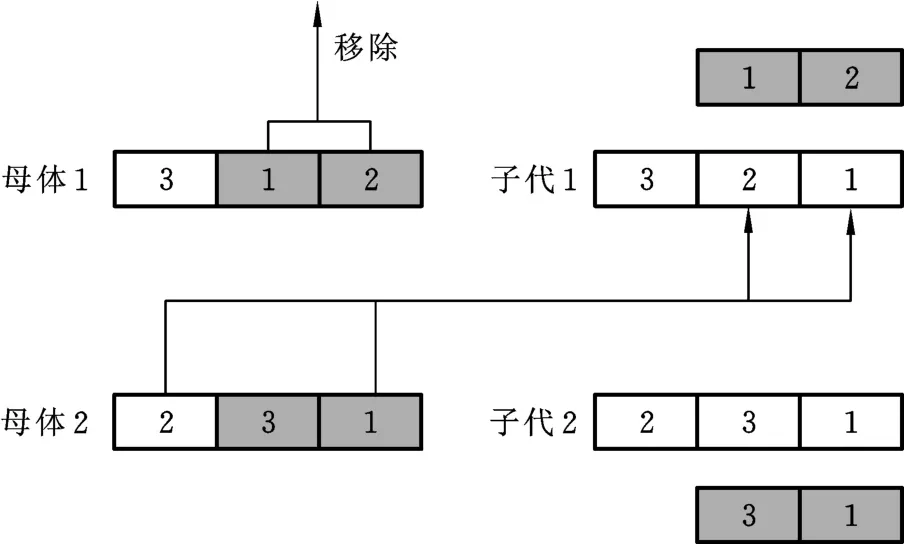
图5 单点机器人交叉Fig.5 Single-poin t robot crossover

混合灰狼算法的流程如图6所示。

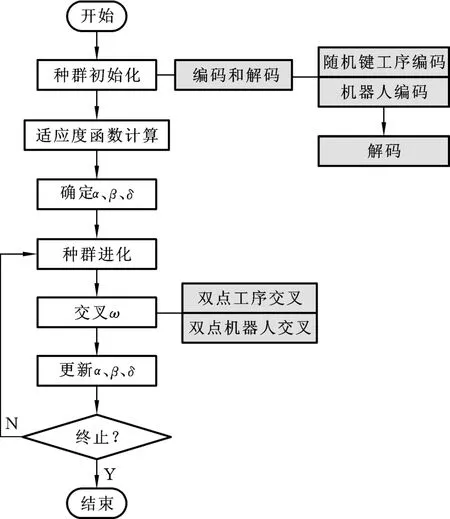
图6 混合灰狼算法流程Fig.6 Flow chart of hybrid grey wolf op tim ization

3 实验结果与分析

为验证HGWO算法的性能，将HGWO算法与GWO算法进行对比。两种算法都采用C语言进行编程，并在同一台电脑上运行，电脑配置为：Intel Core i5 CPU，2.80 GHz and 2.00 GB RAM。实验案例选取大规模U型装配线标杆案例：A rcus111，Barthol148和Scholl297。3个案例的工序数n分别为111、148、297。且每个案例分别设置4种规模的工作站数量：A rcus111中，m=9，13，17，22；Barthol148中，m=10，14，21，29；Scholl297中，m=19，29，38，50。机器人的数量r等于工作站的数量。案例的优先关系和装配时间来自专业装配线网站https：//assembly⁃line⁃balancing.de/。工序在不同机器人上的加工时间在［0.8ti，1.2ti］中随机生成（ti为工序 i的装配时间），单元能耗值在［0.2，3.0］中随机生成［12］。算法终止条件设置为运行时间n×n×10和n×n×20。

算法对比前，采用M initab中的田口实验对算法进行参数校验，得出最佳参数组合。HGWO最佳参数组合为：种群规模40，交叉概率0.7；GWO最佳参数组合为：种群规模40。

对比试验中，每一个案例运行10次，获取总能耗的最小值和平均值。表1、表2分别展示了2种终止条件下的对比结果。

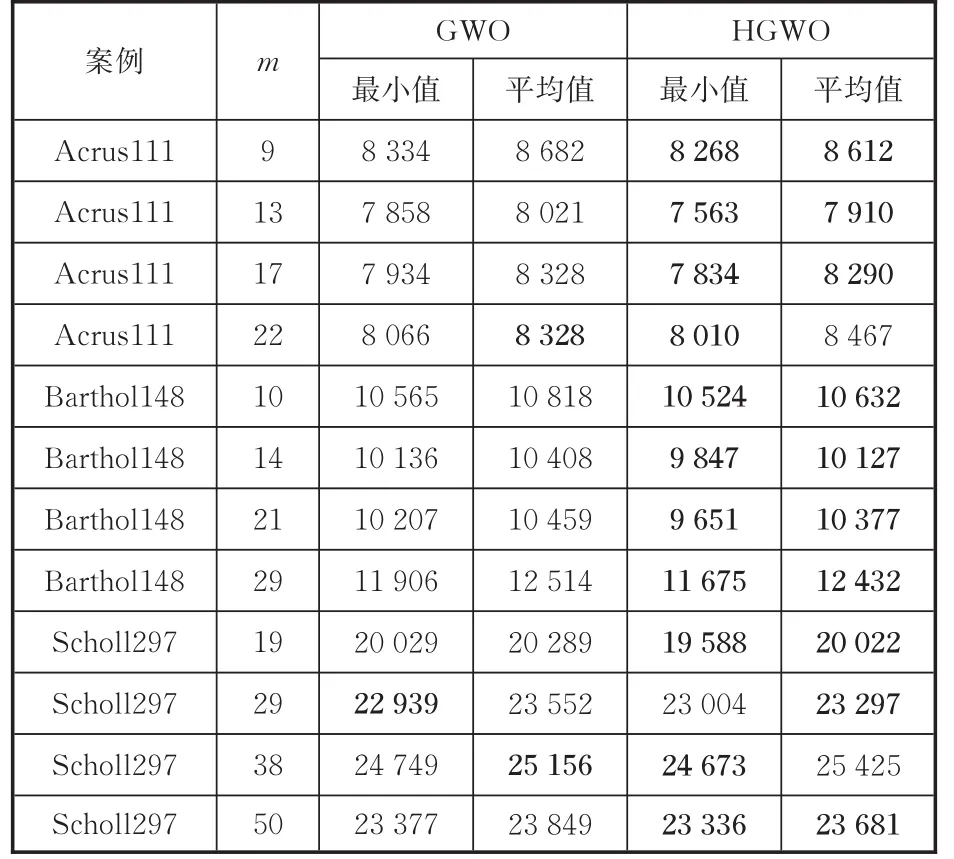
表1 终止条件为n×n×10的对比结果Tab.1 Com parative resu lts of term inal condition n×n×10

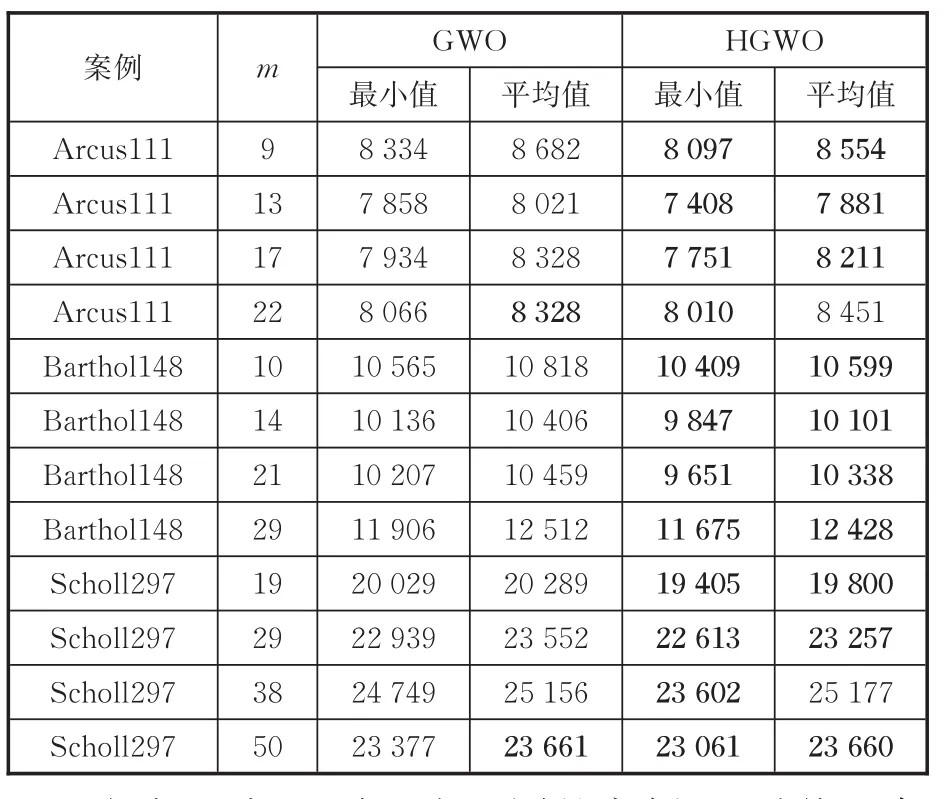
表2 终止条件为n×n×20的对比结果Tab.1 Com parative results of term inal condition n×n×20）

由表1、表2可知，在不同的案例，两种终止条件下，HGWO所获得能耗最小值和平均值基本都要小于GWO获取的结果。从而证明了所提出的HGWO算法在求解机器人U型装配线能耗优化问题时具有显著的优越性。

图7为HGWO算法求解A rcus111问题的收敛图，即能耗随迭代次数的变化曲线。由图7可知，在算法运行到70代左右时，算法收敛很快；70～308代时，算法收敛变慢，但种群还在持续进化；308代之后，算法基本不再进化。这表明HGWO算法在求解该问题时具有较好的收敛性。

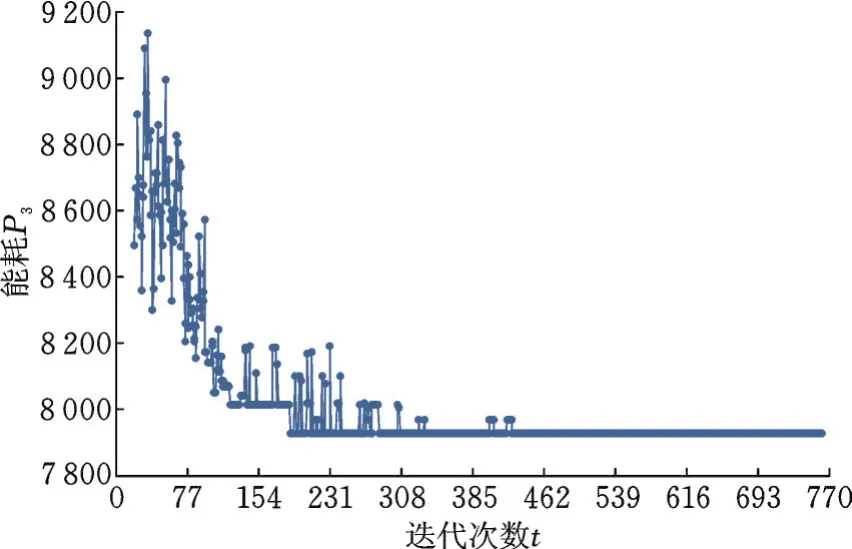
图7 HGWO算法收敛图Fig.7 Convergence of HGWO algorithm

为分析能耗的降低是否会影响装配线常规目标——节拍值，本文分析了不同方案的工序分配、机器人分配和目标值。表4展示了两种方案的工序和机器人布局，以及节拍值和能耗值。所分析的案例为A rcus111标杆案例，工序数为111，工作站和机器人数为9。方案1为HGWO算法的第一代最优解的分配方案，方案2为算法优化后，得到的最优解的分配方案。由表4可知，由于方案1中工序分配很不均匀，其最终的节拍值和能耗都很大，分别为755和9 252.28。方案2工序分配比较均匀，每个工作站的工序数量都在13左右，且节拍值和能耗都要小于方案1，分别为709和8 756.12。由此可以发现，在算法优化能耗的同时，节拍值也在逐渐减小，表明能耗的降低也会影响装配线的传统目标——节拍。因此，在实际装配线布局时，企业可以以能耗为目标，来平衡装配线的生产负载。这样既可以达到负载均衡的目的，也能降低企业的生产能耗。

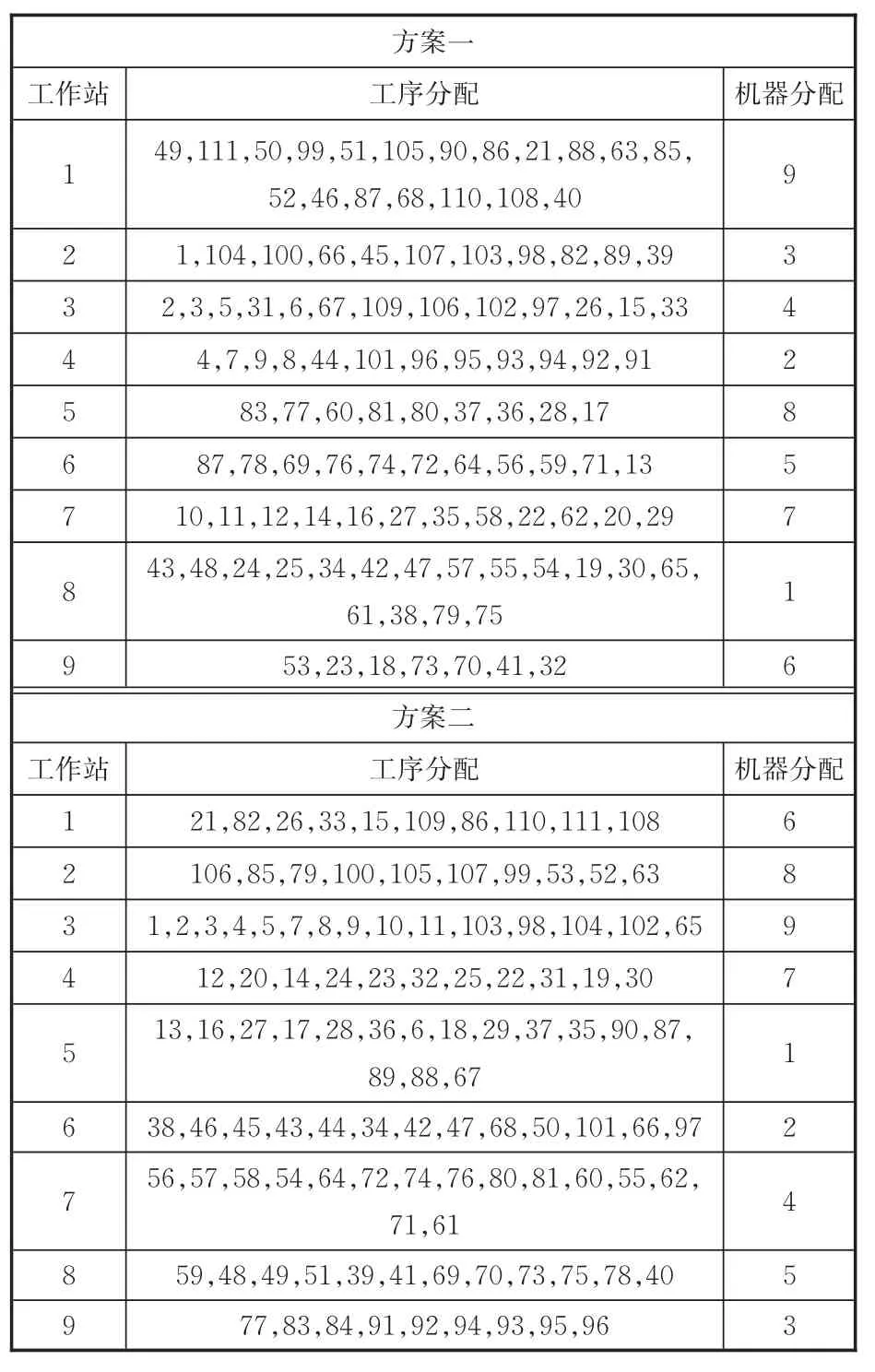
表4 能耗节能方案对比表Tab.4 Com parative results of the energy consum p tion p lans

4 结语

针对当前逐渐推广的机器人U型装配线问题，本文以能耗为优化目标，介绍了机器人U型装配线平衡问题，并采用混合灰狼算法求解了该问题。算法采用随机键编码方式实现工序编码，将连续问题离散化。针对问题中的工序分配和机器人分配，引入两种交叉算子，实现算法中最低等级灰狼之间的信息交流。通过与原始灰狼算法的对比，验证了混合灰狼算法性能的可行性和有效性。在未来的研究中，可以将生产中的负载问题与能耗问题进行协同优化。