基于多目标遗传算法的双机器人协调焊接路径规划

2018-09-08侯仰强王天琪岳建锋贾振威

中国机械工程 2018年16期

侯仰强王天琪岳建锋贾振威

天津工业大学天津市现代机电装备技术重点实验室，天津，300387

0 引言

双机器人协调焊接系统在提高焊接效率、保证焊接质量等方面具有独特的优势，已广泛运用于各种工业焊接生产线［1］。为使双机器人可以快速、无碰撞地完成高质量焊缝的焊接任务，需要事先通过一定的算法对其进行焊接路径的规划，将规划好的机器人姿态信息导入机器人控制柜中，使其控制焊接机器人按照规划的路径进行焊接。

路径规划技术作为人工智能研究中的经典问题，众多学者对其开展了广泛的研究，提出了解决此类问题的多种算法，如人工势场法、遗传算法、模拟退火算法等［2⁃3］。针对双机器人协调焊接作业问题，在路径规划时需要考虑焊枪姿态、焊接位置、机器人运动平稳性等多种因素，既要保证焊缝质量良好，又要保证机器人运动平稳、双机器人之间无碰撞，因此双机器人协调焊接路径规划可看为多目标规划问题［4］。传统的多目标规划优化算法将多目标函数进行加权或约束，从而将多目标优化问题转化为单目标优化问题，再利用成熟的单目标优化算法进行求解［5］。这种方法虽然简便、快捷，但目标函数加权值的分配具有较强的主观性，优化效果不佳。多目标遗传算法是近几年针对多目标优化问题发展起来的新型优化算法，该方法高效实用，不受问题性质的限制及人为主观性的约束，可搜索出全局最优解［6⁃8］，从而为双机器人协调焊接路径规划多目标优化问题提供了良好的解决办法。

本文提出一种基于多目标遗传算法的双机器人协调焊接路径规划方案。首先对影响焊接质量和双机器人协调运动柔顺性的各参数进行数学建模来建立各个子目标，再利用多目标遗传算法进行优化参数的求解，求出焊接的最佳路径。以常见输油管道中两管相贯形成的“马鞍形”空间焊缝为例，对双机器人协调焊接路径进行了焊接试验验证。

1 目标函数建模

1.1 焊缝离散化

复杂空间焊缝可以离散成足够多的焊缝离散点，进行实际焊接时，焊枪在某些相邻焊缝离散点上的焊接姿态没有变化［9］。因此，为了简化规划运算，需要对焊缝进行离散，这些离散点可以表征该空间焊缝的所有特征。路径规划时只要保证焊枪以特定的姿态依次通过这些焊缝离散点，就可完成整条焊缝的焊接。文中采用的是一种基于相邻焊缝离散点之间的弦公差和步长的焊缝离散方法，该方法可有效避免传统等距取点离散法造成的焊缝离散点特征信息冗余或信息不足。两相邻焊缝离散点之间的步长与弦公差如图1所示，在进行焊缝离散化操作时，弦公差越小，提取出的焊缝离散点越多，当弦公差一定时，曲率变化大的地方提取的焊缝离散点多。再利用步长来过滤过小间距的焊缝离散点，步长可根据实际焊接的焊缝形状来定。

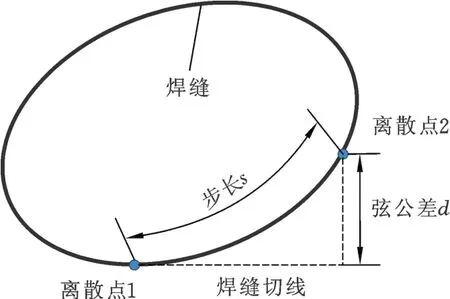
图1 步长与弦公差示意图Fig.1 Schem atic of step length and tolerance

1.2 焊缝质量函数

1.2.1 焊接位置函数

焊缝质量在很大程度上取决于所处的焊接位置，而焊接位置一般用焊缝倾角和焊缝转角来表示，其含义如图2所示。

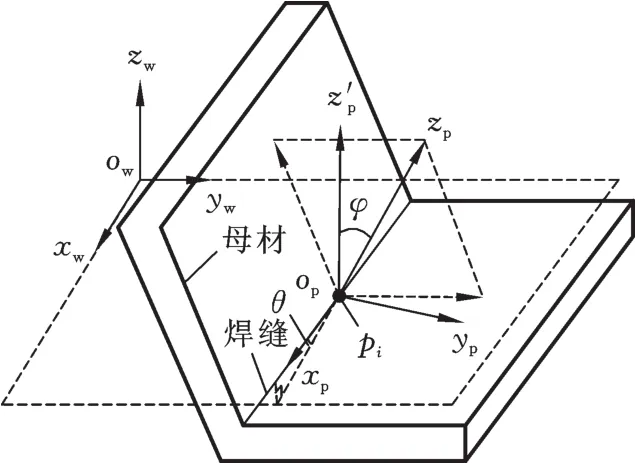
图2 焊缝倾角、转角示意图Fig.2 Schematic of thewelding seam'sangle and corner

图2中，owxwywzw为世界坐标系；pi为焊缝上任意一个离散点；以pi为原点，pi沿焊缝方向的切线为xp轴，两侧母材外法线夹角的平分线为zp轴，通过右手定则确定yp轴来建立焊缝坐标系opxpypzp；根据国家标准GB/16672-1996的定义，焊缝倾角θ为xp轴与平面xwowyw的夹角，取值范围为［0,2π］；焊缝转角φ为将zp轴绕xp轴转动到与zw轴平行（即轴）时所转过的角度，取值范围为［0,2π］；两参数对焊缝质量的影响用下式来描述［10］：

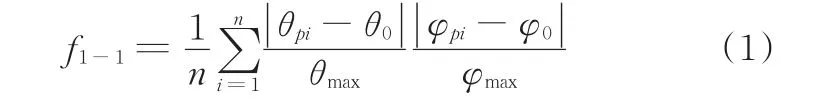
式中，f1-1为整条焊缝的焊接位置函数；n为焊缝离散点的个数；θpi、φpi、θmax、φmax分别为在焊缝离散点 pi处的焊缝倾角和焊缝转角以及所允许的最大值；θ0为焊缝倾角调节参数，在船形焊位形时一般取8°～12°；φ0为焊缝转角调节参数，在船形焊位形时一般取0°～5°。

1.2.2 焊枪姿态函数

实际焊接时，除焊接位置参数外，焊枪姿态也会对焊接质量产生影响。焊枪姿态一般用焊枪的工作角、行走角以及自转角来描述，其具体含义如图3所示。

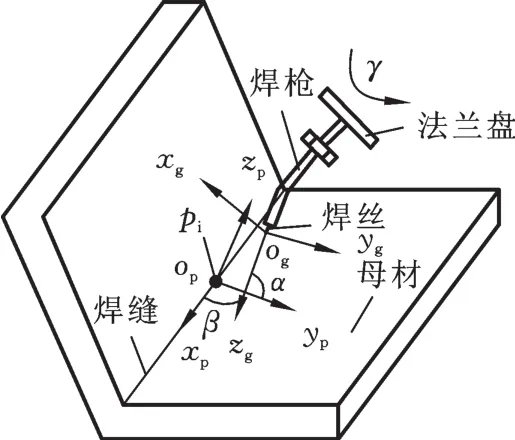
图3 焊枪姿态示意图Fig.3 Schem atic ofweld ing gun orientation

图3中，以焊枪伸出的焊丝末端为坐标原点og，焊枪轴线为zg轴，以既垂直于机器人末端法兰盘中心轴线又垂直于焊枪轴线的轴为xg轴，根据右手定则确定yg轴来建立焊枪坐标系ogxgygzg；经查阅相关文献，定义焊枪工作角α为zg轴与yp轴的夹角，取值范围为［0,π］；焊枪行走角β为zg轴与xp轴的夹角，取值范围为［0,π］；焊枪自转角γ为zg轴自身旋转的角度，取值范围为［0,2π］；通过工程实践证明，焊枪的自转角对焊缝成形质量的影响极其微弱，可忽略不计。焊枪姿态函数对焊缝质量的影响可通过下式来描述［2］：

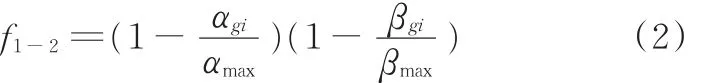
式中，f1-2为整条焊缝的焊枪姿态函数；αgi、βgi、αmax、βmax分别为焊接pi点处的焊枪工作角和焊枪行走角以及它们所允许的最大值。

综合焊接位置参数以及焊枪姿态函数，所建立的焊缝质量函数为

式中，f1为整条焊缝的焊缝质量函数。

1.3 机器人运动平稳性函数

机器人进行焊接工作时，当机器人从当前焊缝离散点位姿向下一个焊缝离散点位姿进行转换的过程中，需要保持焊枪的平滑过渡。机器人关节变化太剧烈会引起焊枪的抖动，进而影响焊接电弧的抖动，对焊接质量产生影响［11］。定义相邻焊缝离散点间机器人关节的变化量为机器人运动平稳函数，其表达式如下：

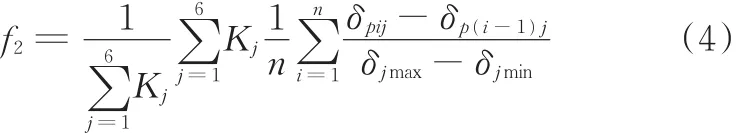
式中，f2为机器人运动平稳性函数；Kj为机器人第j关节的加权系数，其值的选取根据机器人各关节转动惯量的大小来定；δpij、δp（i-1）j分别为焊接 pi点以及 pi-1点时的机器人的关节角；δjmax、δjmin分别为机器人第j关节的关节角所允许的最大值、最小值。

1.4 双机器人位置约束及碰撞函数

双机器人协调焊接系统中的一台机器人上装载焊枪，作为焊接机器人，另一台机器人上装载夹具，作为夹持机器人，其协调关系如图4所示。

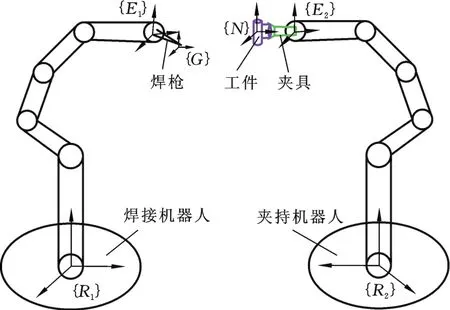
图4 双机器人协调焊接系统简图Fig.4 Sim p lified diagram of the dual”robot coord inate welding system

图4中，{R1}、{R1}分别为焊接机器人、夹持机器人的基坐标系；{E1}、{E2}分别为焊接机器人、夹持机器人末端法兰盘坐标系；{G}为焊枪坐标系即工具坐标系；{N}为工件坐标系。其协调运动空间位置约束为

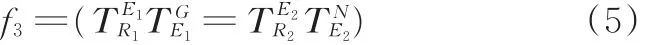
式中，f3为双机器人协调焊接系统空间约束函数；、分别为焊接机器人末端法兰盘坐标系相对于机器人基坐标系、焊枪坐标系相对于末端法兰盘坐标系的姿态齐次坐标变换矩阵；

2、分别为焊接机器人末端法兰盘坐标系相对于机器人基坐标系、焊枪坐标系相对于末端法兰盘坐标系的姿态齐次坐标变换矩阵。

双机器人在进行协调焊接工作时，由于工作空间存在一定的交叉，所以机器人经过重合工作空间区域时可能会产生碰撞。为了避免此类现象的发生，定义双机器人碰撞函数：

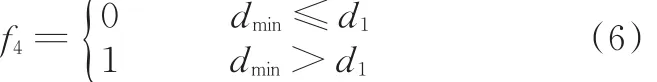
式中，f4为双机器人碰撞函数；dmin为双机器人之间的最短距离；d1为两机器人运动的安全阈值，其值的大小可视情况而定。

2 多目标遗传算法

进行双机器人协调焊接路径规划时，既要保证在实际焊接过程中的焊接倾角、焊缝转角以及焊枪工作角变化不大，又要满足机器人运动平稳、双机器人之间无碰撞的要求，因此它是一个目标函数不唯一且需要同时满足的多目标优化问题［12⁃14］。

2.1 算法流程

通过对双机器人协调焊接系统各目标函数进行建模，确定了各优化子目标。然后对各目标进行适应度分配，并进行遗传操作直至求出满足优化指标的值，其具体的操作流程如图5所示。

图5 算法流程图Fig.5 Flow chart of algorithm

产生初始路径后，将焊接位置函数、焊枪姿态函数等对路径进行搜索，获得一条假设路径，利用机器人关节稳定性函数及碰撞函数对路径进行修正。

2.2 遗传算子选取

在进行选择、交叉以及变异等遗传操作时，为了快速有效地规划出可行路径，需要用到遗传算子，文中用到的遗传算子如下：

（1）选择算子x1。采用随机遍历抽样的方式在种群中选择优势个体，根据优胜劣汰的选择方式，将适应值小的路径进行变异。

（2）插入算子x2。因为空间曲线焊缝为连续曲线，而产生的初始焊接路径可能会出现不连续的情况，因此采用插入算子在不连续的路径中插入部分节点，形成连续路径。

（3）交叉算子x3。交叉算子是遗传算法中的核心算子，对具有相同路径节点的初始路径进行交叉重组，通过交叉操作可以大大提高算法的搜索能力。文中用到的交叉过程为

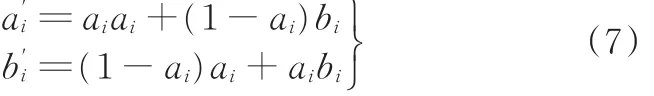
式中，ai、bi表示进行交叉操作前后，两条染色体上的第i个基因。

（4）变异算子x4。利用变异算子来对不理想路径进行局部修正，对较差的路径对应节点进行变异，提高路径搜索及规划的效率。

3 焊接实例验证

利用实验室现有设备对双机器人协调焊接路径进行了试验验证，两机器人分别采用的是ABB公司的IRB1410和IRB2400型六轴工业机器人，电焊机采用Fronius公司的CM T 4000R型焊机。试验工件选用的是两个外径均为140mm，壁厚为5mm的钢制圆形管道，焊缝为两圆管相贯形成的“马鞍形”空间焊缝，其形状如图6所示。

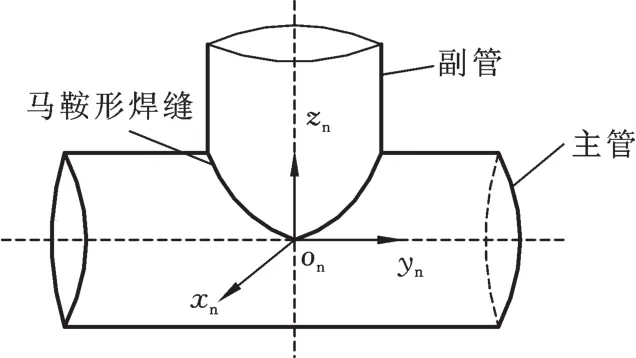
图6“马鞍形”焊缝示意图Fig.6 Schem atic of“sadd le”weld

为了确定焊接的初始路径，需要对两管相贯形成的焊缝进行数学建模。如图6所示，将两管中轴线的交点设为原点on，以两管中轴线组成平面的法线方向为xn轴，主管中轴线的方向为yn轴，副管中轴线的方向为zn轴，建立坐标系onxnynzn，则形成的焊缝可表示为

3.1 规划结果

首先按照1.1节所述方法对焊缝进行离散化，弦公差d设置为1mm，步长s设置为2.5mm，其离散后效果如图7所示，离散后形成的焊缝离散点个数n为45。

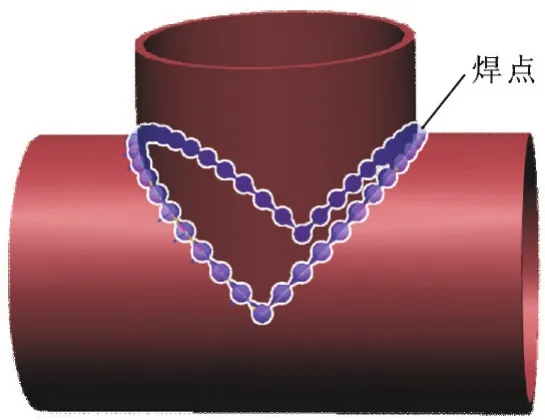
图7 焊缝离散图Fig.7 W eld d iscrete figu re

按照第2节所述的多目标遗传算法在数据处理软件中对双机器人协调焊接“马鞍形”焊缝进行路径规划，所得结果如图8所示。机器人1为装载焊枪的机器人，机器人2为加持工件的机器人，J1～J6分别表示机器人的第1关节～第6关节。由结果可以看出，焊缝倾角、焊缝转角、焊枪工作角以及焊枪行走角的变化都在±0.05°以内，焊缝质量比较稳定；两机器人各关节角变化比较光滑，运动状态平稳。

3.2 焊接验证试验

3.2.1 仿真试验

将规划好的路径结果导入机器人离线编程软件RobotStudio中，对路径进行仿真，仿真系统如图9所示。

利用软件中的碰撞监测功能对两机器人整个协调焊接过程进行碰撞监测，两机器人运动的安全阈值dl设置为40mm，结果如图9b所示，由监测结果来看，在整个焊接过程中未发生碰撞现象。借助离线编程功能，将上述路径生成相应的Rapid程序，以便导入实际的机器人控制柜中。

3.2.2 实际焊接

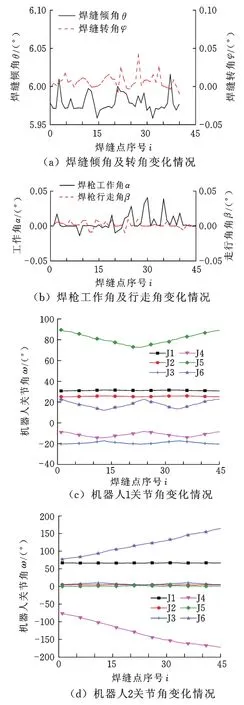
图8 规划结果Fig.8 Planning resu lts

为了验证实际焊接的焊缝质量情况，对“马鞍形”空间焊缝进行了实际焊接试验，采用CM T焊接工艺，焊接电流为187 A，焊接电压为22.7 V，送丝速度为6 m/m in。将前述生成的Rapid程序分别导入两机器人，控制机器人进行实际焊接。在进行焊接时，夹持机器人末端进行旋转运动，焊接机器人沿马鞍形轨迹焊接。双机器人在焊接过程的部分姿态及焊接后的工件如图10所示，可以看出，所焊接的“马鞍形”焊缝成形质量良好，满足焊接工艺要求。