一类半线性椭圆型方程边值问题的正径向解

李小帅，钟金标

(安庆师范大学数学与计算科学学院，安徽安庆246133)

文献[1]讨论了问题：

为有界光滑区域。文献[2]讨论了半线性椭圆型方程：

的正径向解是否存在，并利用拓扑度理论证明了其正径向解的存在性。文献[3-4]分别讨论了

解的存在性。受文献[1-4]的启发，利用不动点理论证明下列半线性椭圆型方程边值问题：

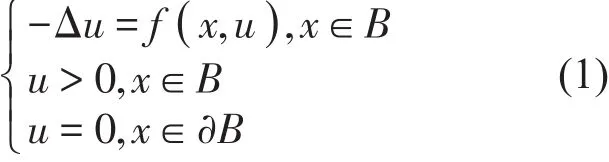
正径向解的存在性，并讨论解的唯一性及不可解性。这里B⊂Rn( n ＞1)是以球心为原点的单位球，Δ是n维Laplacian算子，f∈C[ B ×[0 ,∞ ) ]且关于u在0处是超线性的，比文献[1]中非线性项更具一般性。

假定问题(1)中的非线性函数满足或部分满足下列条件：

(H1)f( x ,s):B×[0 ,+∞ ) →[0 ,+∞)是连续的且关于s是单增的。

(H3)f:B×R+→R+是Lipschitz连续的，Lipschitz系数为L且L＜λ1，其中λ1是-Δ算子0-Dirichlet边值问题的第一特征值。

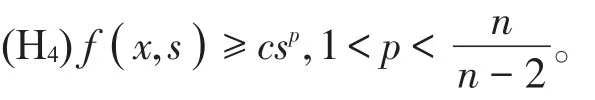
1 存在性

考察(1)式的径向形式

其中，r∈[0 ,1)。

定理1设(H1)成立，则(2)式若有解必为正解。

证明 由条件(H1)知f( x ,u ) ≥0，从而

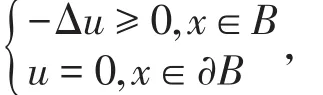
由上调和函数的极值原理知，u≥0。

引理2[5]（不动点定理）设X是一个Banach空间，C是X的一个闭凸子集。若T是C到C的一个紧映射，R为一个正常数，对满足||u||=R的任意u∈C，有u≠tT()u,0≤t≤1，则T有一个不动点u∈C，且||u||≤R。

定理3 设(H1)，(H2)成立，则(1)式存在有界正径向解。

证明 设X=C[ 0 ,1 ]，K≜{ u | u∈X,u≥0,u′(0 ) =0,u(1 ) = 0}，则K为X的一个闭凸子集。定义算子T:K→K：

结合(H1)，这里T:K→K是紧正算子[6]。

设u是u=tT(u ) 的一个解，t∈[ 0 ,1]，则

对足够小的常数τ，设||u||∞= τ，利用(H1)有

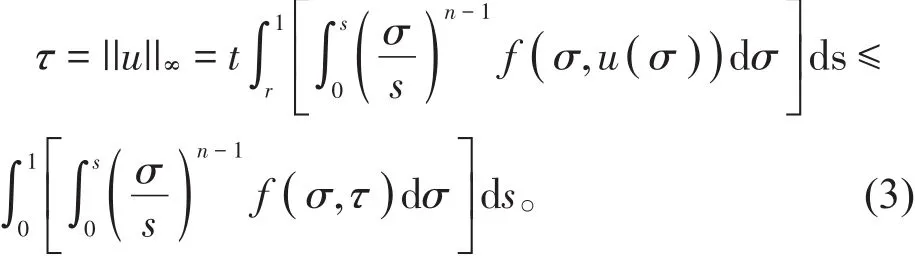
由条件(H2)知，对足够小的τ，有，即矛盾。因此对常数τ，对∀u∈K有u≠tT()u,0≤t≤1。由引理2知，T有一个不动点u∈K，即

所以(2)式存在正径向解，即(1)式存在正解。

例1考察问题是否存在有界正径向解，这里B∈Rn( n ＞1 )是以球心为原点的单位球。

证明 对于(4)式，f(x ,s)=s2，满足条件(H1)、(H2)，由定理3知(4)式存在有界正径向解。

2 唯一性

非线性方程边值问题解的唯一性一般需通过附加适当的条件得到。

定理4 如果(H3)成立，那么(1)式至多只有一个解。

证明 设u与v为(1)式的两个解，

-Δu=f( x ,u )，-Δv=f( x ,v )，u-v=0,x∈ ∂B，则

将(5)式两边乘上u-v，并在B上积分，利用Green恒等式、Poincare不等式得到

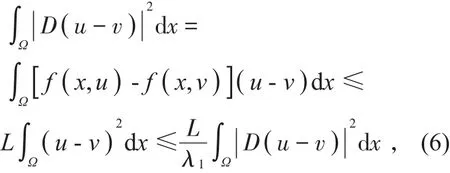
由条件(H3)知，＜ 1，与(6)式矛盾，所以u=v，即至多只有一个解。

3 不存在性

下面考察的正径向解，则(7)式转换为下面问题

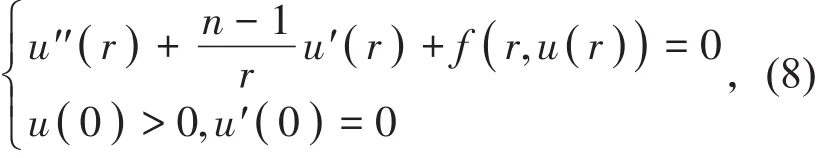
其中r= |x|。

定理5 设n ≥ 3，条件(H1)，(H4)成立，则(8)式不存在正径向解。

证明 设u(r)为(8)式的正径向解，则u(r)满足

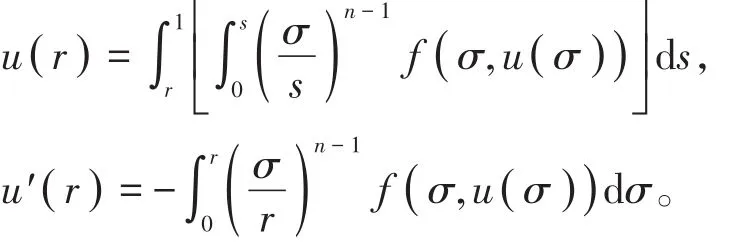
由(H1)知u′(r )＜0，从而u(r)单减，所以

则

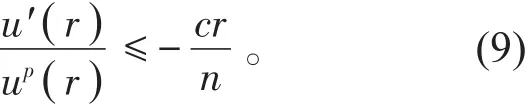
对(9)式从0到r积分得

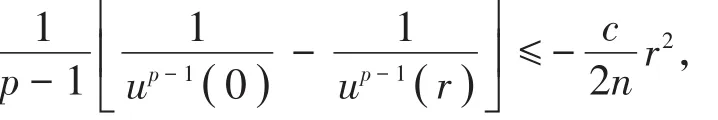
于是

考察F(r)=ru′(r)+(n -2) u(r)，断言F(r )≥0，若不然，存在r0＞0，使得F( r0)=r0u′(r0)+( n -2) u(r0)＜0。 因 为 F′(r)=(r u′(r))′+( n -2) u′(r)=-rf(r ,u(r ) )＜0，所 以 ru′(r)+( n -2) u(r)＜F( r0),r＞ r0，从而

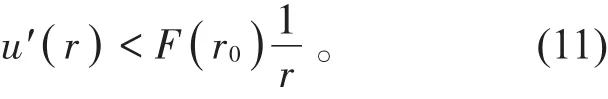
对(11)式从r0到r积分得到u(r)-u( r0)＜F( r )ln→ -∞,r→ +∞，得u(r )=∞矛盾，所

00以F(r ) ≥0。因此

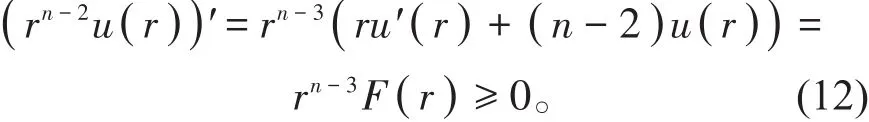
对(12)式 从0到r积 分得rn-2u(r )≥Cˉ，即u(r ) ≥ Cˉr-(n-2),r≥ 1。结合(10)式得

满足条件(H1)、(H4)，故由定理5知例2无解。